6.8 note

paxos算法_初步感知

Paxos算法保证一致性主要通过以下几个关键步骤和机制：

 

准备阶段

 

- 提议者向所有接受者发送准备请求，请求中包含一个唯一的编号。

 

- 接受者收到请求后，会检查编号，如果编号比它之前见过的都大，就会承诺不再接受编号更小的提议，并回复提议者，告知自己已接受过的最大编号的提议。

 

提议阶段

 

- 提议者收到多数接受者的回复后，根据回复内容来确定提议的值。如果有接受者在回复中包含了已接受的提议值，提议者就从中选择编号最大的提议值作为自己要提议的值；如果没有，提议者就自己选择一个值。然后，提议者将选定的值和编号一起作为提议发送给接受者。

 

- 接受者收到提议后，只有在之前没有承诺过不接受该提议，并且提议的编号不小于它之前见过的最大编号时，才会接受该提议。

 

学习阶段

 

- 一旦有多数接受者接受了某个提议，这个提议就被认为是达成了一致。此时，系统中的其他节点可以通过学习这个已达成一致的提议来更新自己的状态，从而保证整个系统的一致性。

 

通过这一系列的步骤，Paxos算法能够在分布式系统中，即使存在节点故障、消息丢失等情况，也能保证最终达成一致的状态，确保数据的一致性和正确性

---

举个栗子🌰

假设你和一群朋友打算一起去看电影，但是对于看哪部电影大家有不同的想法，这时就可以用类似Paxos算法的方式来达成一致：
 
准备阶段
 
- 你主动站出来成为“提议者”，你先给每个朋友发消息说：“我准备提议看一部电影，我现在的提议编号是1（这个编号是唯一且不断递增的），你们之前有没有收到过其他人的提议呀？如果有，是关于看什么电影的，编号是多少呢？”
 
- 朋友们收到消息后，会查看自己收到过的提议编号。如果你的编号比他们之前收到的都大，他们就会回复你，比如有的朋友会说：“我之前没收到过提议。”有的朋友可能会说：“我之前收到过提议看电影A，编号是0。”同时，他们会承诺不再接受编号小于1的提议。
 
提议阶段
 
- 你收到朋友们的回复后，发现有朋友提到了之前看过的提议看电影A，编号是0，而你的编号是1更大，所以你可以选择自己重新提议看电影B，也可以选择就提议看电影A。然后你把你的提议（比如看电影B，编号是1）发给朋友们。
 
- 朋友们收到你的提议后，会检查这个提议的编号是不是不小于他们之前见过的最大编号，并且他们之前没有承诺过不接受这个提议。如果满足条件，他们就会接受这个提议，比如同意一起去看电影B。
 
学习阶段
 
- 当有超过一半的朋友都接受了看电影B这个提议，那么就相当于大家达成了一致，决定一起去看电影B。然后大家就可以一起去看电影，保证了所有人的行动一致。
 
在这个过程中，即使有朋友一开始没收到消息，或者中间有消息延迟等情况，只要最终大家都按照这个流程来，就能保证最终能就看哪部电影达成一致，就像Paxos算法在分布式系统中保证数据一致性一样。

---

Paxos算法这样的一致性算法的设计思路是基于对分布式系统中一致性问题的深刻理解和长期的研究探索逐渐形成的，主要考虑以下几个方面：

 

问题分析

- 分布式系统中存在节点故障、网络延迟、消息丢失等问题，要保证数据在多个节点间的一致性，需要设计一种能在复杂环境下达成共识的机制。

- 借鉴现实生活中类似议会投票等协商场景的经验，思考如何通过类似的投票、协商过程让分布式系统中的节点就某个值达成一致。

 

关键原则确定

- 安全性原则是确保只有被多数节点认可的值才能被选定，防止出现不一致的情况。就像在选举中，只有获得多数选票的候选人才能当选，保证结果的唯一性和确定性。

- 活性原则是保证系统能够不断推进，不会因为某些故障或异常而陷入死循环或无法做出决策的状态。例如，通过给提议编号等方式，让系统能够区分不同的提议，避免重复或无效的提议导致系统停滞。

 

逐步构建算法

- 先设计准备阶段，让提议者了解系统中已有的提议情况，同时让接受者承诺不接受低编号提议，为后续提议的顺利进行奠定基础。这一步就像在会议前先收集各方意见，确定大家的基本立场。

- 再设计提议阶段，提议者根据准备阶段的反馈确定提议值并发送给接受者，接受者根据一定规则决定是否接受提议。这个过程类似会议中的讨论和表决环节。

- 最后通过学习阶段，让系统中的其他节点能够得知达成一致的结果，从而实现整个系统的一致性更新。

 

通过这样从问题分析到关键原则确定，再到逐步构建算法的过程，经过不断地理论推导、实践验证和优化，最终形成了Paxos算法这种能够有效保证分布式系统一致性的经典算法。

 

 

rabbitmq 6种模式

 

sql连接

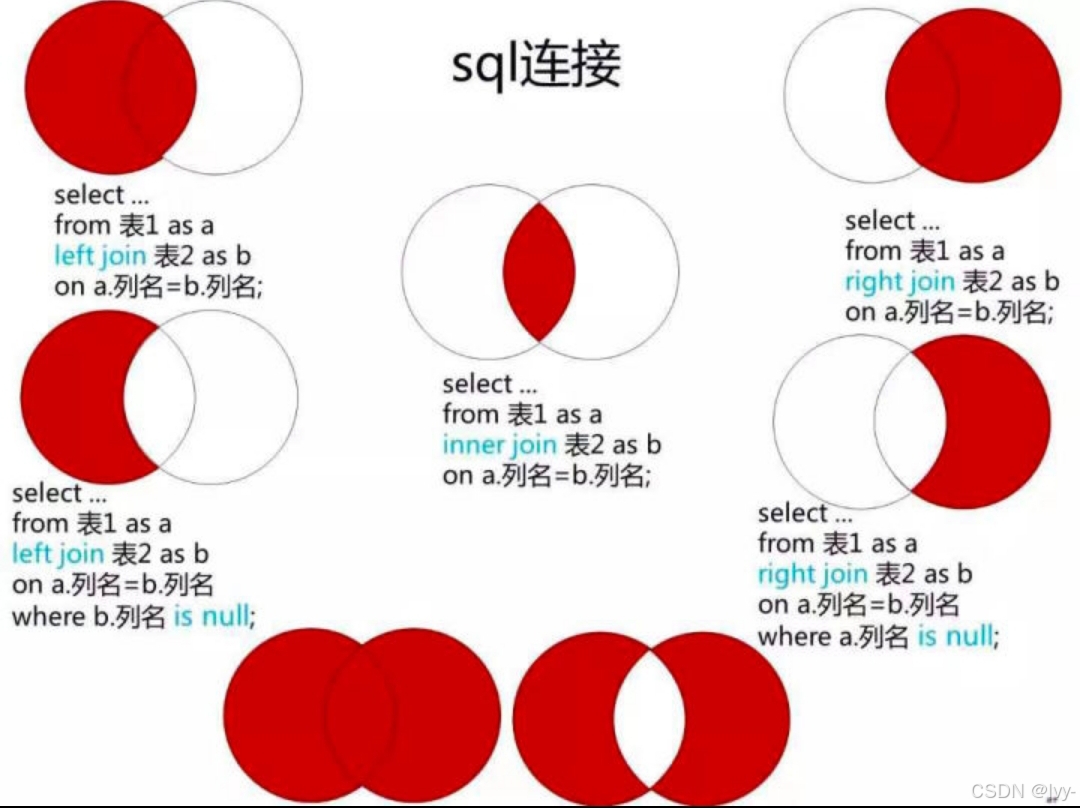
 select p.FirstName,p.LastName,a.City,a.State
from
person p left join address a
on
p.personid=a.personid

 

2的幂再和，二进制取模相加==n

 1. 分解n为2的幂次：
 
- 利用二进制特性，n的每一位1对应一个唯一的2的幂次（如n=10=8+2=2³+2¹，对应powers=[2,8]）。
 
- 通过不断对n取余和整除2，提取每一位二进制位，将对应的幂次存入 powers 数组。
 
2. 处理查询：
 
- 每个查询给出一个区间 [l, r] ，表示求 powers[l] * powers[l+1] * ... * powers[r] 的结果。
 
- 由于结果可能很大，每次乘法后都对 1e9+7 取模（利用模运算性质防止溢出）。
 
3. 注意点：
 
- 使用 long long 存储中间结果，避免整数溢出。
 
-  powers 数组的下标直接对应查询中的区间端点（如查询 [0,2] 表示取前3个幂次相乘）。
 
示例理解：

• - 若 n=15 （二进制 1111 ），则 powers = [1,2,4,8] 。
• - 查询 [0,2] 对应计算 1*2*4=8 ，查询 [1,3] 对应 2*4*8=64 。

class Solution {
public:
    vector<int> productQueries(int n, vector<vector<int>>& queries) {
        // 造powers数组
        vector<int> powers;
        // 由n变到1powers数组
        for(int i=0,i1=1,j=0;n>0;)
        {
            i=n%2;
            if(i==1) {powers.push_back(i1);j++;}
            n/=2;i1*=2;
        }
        // return powers;
        // 造answers数组
        vector<int> answers;
        for(int i=0; i<queries.size(); i++)
        {
            long long ans=1;
            int c=1e7;
            for(int k=queries[i][0]; k<=queries[i][1]; k++)
            {ans=((ans%c)*(powers[k]%c))%c;}

             //求区间乘积
            //利用了（a*b）%c=((a%c)*(b%c))%c 拆分取模，防止溢出
            answers.push_back(ans);
        }
        return answers;
    }
};

 

爬楼梯

class Solution {
public:
    int climbStairs(int n) 
    {
        if(n<3) return n;
        vector<int> dp(n+1);
        dp[1]=1,dp[2]=2;
        
        for(int i=3;i<=n;i++)
        {
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};

接雨水

这段代码用「栈」来计算接雨水的量，核心逻辑是：

从左到右遍历每个柱子，用栈记录「可能成为左边边界」的柱子下标。

当遇到更高的柱子（右边界）时，计算两者之间的「凹槽储水量」：

 

1. 弹出栈顶（中间柱子），若栈空则无法形成凹槽，跳过。

2. 确定左右边界：新栈顶是左边界，当前下标是右边界。

3. 计算高度差：左右边界的最小值 - 中间柱子高度，得到储水高度。

4. 计算宽度：右边界下标 - 左边界下标 - 1，乘高度得到水量，累加到结果。

 

举例：柱子高度为  [0,1,0,2,1,0,1,3,2,1,2,1] ，

遍历到  i=3 （高度2）时，栈中是  [0,1] （高度0,1），

弹出1（高度1），左边界是0（高度0），右边界是3（高度2），

储水高度 = min(0,2) - 1 = -1？不，这里实际是 min(左边界高度, 右边界高度) - 中间高度，

左边界高度是  height[0]=0 ，右边界是  height[3]=2 ，中间是  height[1]=1 ，

所以储水高度是 0-1？不对！ 哦这里发现描述有误，正确逻辑是：只有左右边界都高于中间柱子时才有储水，

所以当右边界高度 > 中间柱子时，左边界必须存在且高度 > 中间柱子，

此时储水高度 = min(左边界高度, 右边界高度) - 中间高度，

宽度是右边界下标 - 左边界下标 - 1。

 

代码通过栈动态维护左右边界，逐个计算每个凹槽的水量，最终总和就是答案。

 

int trap(vector<int>& height)
{
    int ans = 0;
    stack<int> st;
    for (int i = 0; i < height.size(); i++)
    {
        while (!st.empty() && height[st.top()] < height[i])
        {
            int cur = st.top();
            st.pop();
            if (st.empty()) break;
            int l = st.top();
            int r = i;
            int h = min(height[r], height[l]) - height[cur];
            ans += (r - l - 1) * h;
        }
        st.push(i);
    }
    return ans;
}

双指针

 

 class Solution {

public:

    int trap(vector<int>& height) {

        int ans = 0, left = 0, right = height.size() - 1, pre_max = 0, suf_max = 0;

        while (left < right) {

            pre_max = max(pre_max, height[left]);

            suf_max = max(suf_max, height[right]);

            ans += pre_max < suf_max ? pre_max - height[left++] : suf_max - height[right--];

        }

        return ans;

    }

};

 

dfs超时优化

注意到 十的九次方 

原代码，超时

class Solution {
public:
    int n=0;
    vector<int> ans;

    int findKthNumber(int n, int k) 
    {
        this->n=n;
        for(int i=1;i<10;i++)
        {
            dfs(i);
        }
       
        return ans[k-1];
    }
    
    void dfs(int num)
        {
            if(num>n)
            {
                return;
            }
            
            ans.push_back(num);
            for(int i=0;i<10;i++)
            {
                dfs(num*10+i);
            }
        }
};

数学优化

class Solution {
public:
    long getCount(long prefix, long n) {
        long cur = prefix;
        long next = cur + 1;
        long count = 0;
        while(cur <= n) {
            count += min(n+1, next) - cur;
            cur *= 10;
            next *= 10;
        }
        return count;
    }

    int findKthNumber(int n, int k) {
        long p = 1;
        long prefix = 1;
        while(p < k) {
            long count = getCount(prefix, n);
            if (p + count > k) {
                /// 说明第k个数，在这个前缀范围里面
                prefix *= 10;
                p++;
            } else if (p+count <= k) {
                /// 说明第k个数，不在这个前缀范围里面，前缀需要扩大+1
                prefix++;
                p += count;
            }
        }
        return static_cast<int>(prefix);
    }
};
 
优化思路：
 
1. 字典序规则：
像查字典一样，先比首位，再比第二位。例如：
 

• - 1开头的数（1,10,11,12…）比2开头的数（2,20,21…）更小。

 
2. 关键函数 getCount ：
计算以 prefix （如1、10）开头的数字有多少个≤n。
 

• - 比如 prefix=1 ，n=20时，包含1、10-19、20（共1+10+1=12个）。
• - 计算方式：逐层扩展（1→10→100），每次算当前层有多少个数在n以内。

3.理解

-  p++ 是深入子节点找下一个数，
 
-  p += count 是跳过当前前缀，去下一个前缀找。

---

十叉树

把数字看作树，用子树大小判断第k个数在左子树还是右兄弟：
 

• - 子树够大：钻进左子树（ node*=10 ）。
• - 子树不够大：跳过左子树，去右兄弟（ node++ ）。

通过这种方式，每次跳跃式减少k的范围，效率极高（对数级时间复杂度）。

class Solution {
public:
    int findKthNumber(int n, int k) {
        // 逐层统计 node 子树大小
        auto count_subtree_size = [&](int node) -> int {
            // 子树大小不会超过 n，所以 size 用 int 类型
            // 但计算过程中的 left 和 right 会超过 int，所以用 long long 类型
            int size = 0;
            long long left = node, right = node + 1;
            while (left <= n) {
                // 这一层的最小值是 left，最大值是 min(right, n + 1) - 1
                size += min(right, n + 1LL) - left;
                left *= 10; // 继续，计算下一层
                right *= 10;
            }
            return size;
        };

        int node = 1;
        k--; // 访问节点 node
        while (k > 0) {
            int size = count_subtree_size(node);
            if (size <= k) { // 向右，跳过 node 子树
                node++; // 访问 node 右侧兄弟节点
                k -= size; // 访问子树中的每个节点，以及新的 node 节点
            } else { // 向下，深入 node 子树
                node *= 10; // 访问 node 的第一个儿子
                k--; // 访问新的 node 节点
            }
        }
        return node;
    }
};

 

线程

 

❗模拟➕贪心

要么都变成 1，要么都变成 -1，因此先枚举要变成哪个。

剩下的问题就是一个经典的贪心。

由于乘以 -1 两次之后会变回原数，因此每个下标最多选择一次，且下标选择的顺序没有关系。

不妨假设操作是从左到右进行的。

从左到右考虑每个下标，如果当前值不是目标值，由于后续操作只会影响右边的数，再不操作就没机会了，所以此时必须要选择该下标。

按该贪心思路算出最少操作次数即可，复杂度 O(n) 。

思维题：想到传递的目标判断即可

其实也还可以找奇偶的规律，但是还是这种更好

class Solution {
public:
    bool canMakeEqual(vector<int>& nums, int K) {
        int n = nums.size();

        // 所有值都变成 x 的最少操作次数
        auto check = [&](int x) {
            int cnt = 0;
            vector<int> vec = nums;
            // 从左到右考虑每个下标，如果不是目标值，必须操作
            for (int i = 0; i + 1 < n; i++) if (vec[i] != x) {
                vec[i] *= -1;
                vec[i + 1] *= -1;
                cnt++;
            }
            return vec[n - 1] == x && cnt <= K;
        };

        // 枚举最后变成 1 还是 -1
        return check(1) || check(-1);
    }
};

总结：

1. 枚举目标：结果只有两种可能——全  1  或者全  -1  。所以我们分别试试这两种情况，看哪种能实现（这就是 “枚举” ，把可能的目标全列出来试）。
 
2. 贪心操作：确定目标（比如要全  1  ）后，怎么操作最省次数？
 
- 规则是 “选一个下标  i  ， nums[i]  和  nums[i+1]  都变号” 。而且变号两次等于没变（比如  1  变  -1  再变  1  ），所以每个位置最多操作一次，从左到右处理最合理 。
 
- 举个例子：数字是  [-1, -1, 1]  ，目标要全  1  。从左开始看，第一个数是  -1  （不是目标  1  ），必须操作下标  0  ，让  nums[0]  和  nums[1]  变号，变成  [1, 1, 1]  ，这样一次就解决。如果不操作当前下标，后面操作不影响前面，就永远变不成目标了，所以 “遇到不一样的，必须当下操作” ，这就是贪心的 “贪”—— 抓住当下机会，保证结果最优。

 

移动模拟_优化

原代码

class Solution {
public:
    int N;
    void move(char c, vector<int>& pos, vector<int>& t) {
        if (c == 'L') pos[1] -= 1;
        if (c == 'R') pos[1] += 1;
        if (c == 'U') pos[0] -= 1;
        if (c == 'D') pos[0] += 1;        
        t = pos;
    }
    bool check(vector<int>& pos) {
        if (pos[0] >= 0 && pos[0] < N && pos[1] >= 0 && pos[1] < N) return true;
        else return false;
    }
    vector<int> executeInstructions(int n, vector<int>& startPos, string s) {
        vector<int> res(s.size());
        N = n;
        for (int i = 0; i < s.size(); i ++ ) {
            vector<int> tempos(startPos);
            int temres = 0;
            for (int j = i; j < s.size(); j ++ ) {
                vector<int> t(2);
                move(s[j], tempos, t);               
                if (check(t)) temres ++ ,tempos = t;
                else break;
            }
            res[i] = temres;
        }
        return res;
    }
};

优化：

改用迭代器并内联函数的 C++ 代码（主要修改循环和容器操作部分）：

class Solution {

public:

    int N;

    // 内联移动函数（用引用避免拷贝）

    inline void move(char c, vector<int>& pos, vector<int>& t) {

        switch(c) {

            case 'L': pos[1]--; break;

            case 'R': pos[1]++; break;

            case 'U': pos[0]--; break;

            case 'D': pos[0]++; 

        }

        t = pos; // 更新目标位置

    }

    // 内联边界检查

    inline bool check(const vector<int>& pos) {

        return pos[0] >= 0 && pos[0] < N && pos[1] >= 0 && pos[1] < N;

    }

 

    vector<int> executeInstructions(int n, vector<int>& startPos, string s) {

        vector<int> res(s.size());

        N = n;

        

        // 使用迭代器遍历字符串

        for(auto it_i = s.begin(); it_i != s.end(); ++it_i) {

            vector<int> currentPos = startPos;

            int count = 0;

            

            // 从当前迭代器位置开始遍历

            for(auto it_j = it_i; it_j != s.end(); ++it_j) {

                vector<int> tempPos(2);

                move(*it_j, currentPos, tempPos); // 传入字符值

                

                if(check(tempPos)) {

                    count++;

                    currentPos = tempPos; // 更新当前位置

                } else {

                    break; // 越界则终止

                }

            }

            res[it_i - s.begin()] = count; // 计算索引

        }

        return res;

    }

};

 

主要改动点： 

1. 函数内联：使用  inline  关键字声明  move  和  check  函数（现代编译器可能自动优化，但显式声明更清晰）

 

2. 迭代器替代索引：

- 外层循环用  s.begin() / end()  迭代器遍历

- 内层循环从当前迭代器位置  it_i  开始

- 通过  it_i - s.begin()  计算结果数组索引

 

3. 代码优化：

-  switch  替代多个  if  提高分支效率

-  currentPos  直接修改减少拷贝（原代码中  tempos = t  可直接操作  currentPos ）

-  const  修饰  check  函数参数避免意外修改

 

注意：C++ 中容器迭代器在动态扩容时可能失效，但此处  string  是固定长度，迭代器始终有效，无需担心此问题。

---

内联函数

内联函数是一种用  inline  关键字声明的特殊函数，目的是让编译器在编译时直接把函数代码「嵌入」到调用它的地方，避免普通函数调用的「跳转开销」，提高程序运行速度。

 

举个简单例子：

假设有个函数计算两数之和：

int add(int a, int b) { 

    return a + b; 

}

 

普通调用时，程序会「跳转到函数地址执行代码，再跳转回来」。

如果声明为内联函数：

inline int add(int a, int b) { 

    return a + b; 

}

编译时，编译器会把  add(3,5)  直接替换成  3+5 ，就像你直接写在代码里一样，省去了跳转步骤。

 

关键特点：

1. 编译时替换：不是运行时调用，而是编译阶段直接「展开代码」。

2. 适合简单函数：通常用于代码量少（如几行）、调用频繁的函数（比如循环里的小操作）。

3. 可能被编译器忽略：最终是否内联由编译器决定（太复杂的函数会被拒绝）。

 

优点 vs 缺点：

• - 优点：减少函数调用开销，提升执行效率。
• - 缺点：如果函数被多次调用，会导致目标代码体积增大（用空间换时间）。

总结：内联函数就像「把常用的小工具直接粘在使用的地方」，省去了拿工具的步骤，但粘太多会占地方。