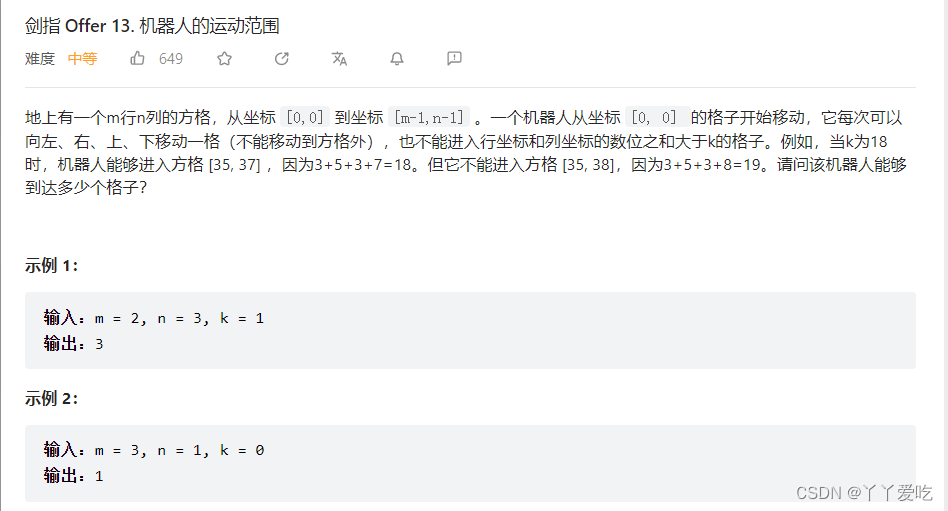
剑指offer12 矩阵中的路径 13 机器人的运动范围 34.二叉树中和为某一值得路径

class Solution {
public:bool exist(vector<vector<char>>& board, string word) {int row=board.size(),col=board[0].size();int index=0,i=0,j=0;if(word.size()>row*col) return 0;//vector<vector<int>> visit[row][col];//标记当前位置有没有被访问过vector<vector<int>> visit(row,vector<int>(col));bool flag=1;while(i<row&j<col){cout<<"board[i][j]: "<<board[i][j]<<endl;if(board[i][j]==word[index]){flag=1;if(index==word.size()-1) return 1;cout<<word[index]<<endl;index++;visit[i][j]=1;if(i-1>=0&&board[i-1][j]==word[index]&&visit[i-1][j]!=1){cout<<"上"<<endl;i=i-1;j=j;}else if(i+1<row&&board[i+1][j]==word[index]&&visit[i+1][j]!=1){cout<<"下"<<endl;i=i+1;j=j;}else if(j-1>=0&&board[i][j-1]==word[index]&&visit[i][j-1]!=1){cout<<"左"<<endl;i=i;j=j-1;}else if(j+1<col&&board[i][j+1]==word[index]&&visit[i][j+1]!=1){cout<<"右"<<endl;i=i;j=j+1;}}else {if(j==col-1&&i<row)//如果到了一行的最后面就调转到下一行 大前提是找不到word[index]相等{cout<<"最末尾的 "<<board[i][j]<<endl;i++;j=0;}else j++;}} return 0;}
};
//写的有点问题,暂时想不到怎么改,先放着,通过用例71/83 卡住的是abcd 但是改了又有问题
无语 看了 答案 都写不对 在类成员里面定义了row和col 就不要重复定义了 不然不知道为什么就开始发疯
class Solution {
public:bool exist(vector<vector<char>>& board, string word) {rows=board.size();cols=board[0].size();for(int i=0;i<rows;i++){for(int j=0;j<cols;j++){if (dfs(board,word,i,j,0)) return true;}}return false;}
private:int rows,cols;bool dfs(vector<vector<char>>& board,string word,int i,int j,int k){if(i>=rows||i<0||j>=cols||j<0||board[i][j]!=word[k]) return false;if(k==word.size()-1) return true;board[i][j]='\0';bool res=dfs(board,word,i+1,j,k+1)||dfs(board,word,i-1,j,k+1)||dfs(board,word,i,j+1,k+1)||dfs(board,word,i,j-1,k+1);board[i][j]=word[k];return res;}
};
先贴出蠢货写出来的东西 审题也审不明白 机器人只能上下左右走 不能一行一行遍历 菜鸟总是这样 自己把自己搞破防
通过用列46/51
class Solution {
public:int movingCount(int m, int n, int k) {int index=0;for(int i=0;i<m;i++){if(add(i)>k) break;for(int j=0;j<n;j++){if(add(j)>k) break;int sum=add(i)+add(j);if(sum<=k) {index++;cout<<sum<<endl;}}}return index;}
private:int add(int x){int sum=0,num=0;while(x){num=x%10;x=x/10;sum+=num;}return sum;}
};
问题出在哪里呢!!!! 就是比如【10,0】虽然数位之和等于1,但是无法通过【9,0】或者其他走过去,假设k=1的话,也就是他妈的他有障碍物啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
aaaa继续做就是要判断边界条件啊啊啊啊啊啊啊啊啊啊啊啊就是判断他是否能进入4个相邻的格子
首先0,0必定可以嗷,check[0,0]置为1。0,0能走到0,1和1,0,那对于0,1和1,0两个点来说,就是判断他们的上面i-1和左边j-1是否可以走,如果可以那就可以从左边和上面分别走过来,能走到当前这个点就置为1,然后左边和上面能走的点都走了之后,还有两个方向没有判断 ,再来判断能不能从右边(i+1)走到左边,下面(i+1)走到上面,如果能走到当前点,就置为1,最后有多少个1,就有多少个机器人能走的格子。
class Solution {
public:int movingCount(int m, int n, int k) {int index=0;int check[m][n];//不能直接写check[m][n]也不能check[m][n]={0},第一次无法保证元素全为0 ,第二个会报错memset(check,0,sizeof(check));//memset进行内存清零,可以将一块内存设置为指定的值check[0][0]=1;for(int i=0;i<m;i++){for(int j=0;j<n;j++){int sum=add(i)+add(j);if(sum<=k) {if(i-1>=0&&check[i-1][j]==1||j-1>=0&&check[i][j-1]==1) check[i][j]=1;}}}for(int i=0;i<m;i++){for(int j=0;j<n;j++){int sum=add(i)+add(j);if(sum<=k) {if(i+1<m&&check[i+1][j]==1||j+1<n&&check[i][j+1]==1) check[i][j]=1;}}}for(int i=0;i<m;i++){for(int j=0;j<n;j++){int sum=add(i)+add(j);if(check[i][j]) {index++;}}}return index;}
private:int add(int x){int sum=0,num=0;while(x){num=x%10;x=x/10;sum+=num;}return sum;}
};
和上题目类似,属于典型的搜索&回溯算法
先了解一下BFS模板
不需要当前遍历到哪一层,BFS模板
while queue 不空cur=queue.front();queue.pop();for 结点 in cur的所有相邻节点if 该节点有效且没被访问过:queue.push(该结点)
需要确定遍历到哪一层,比如之前写过一题打印二叉链表
level=0
while queue不空:size=queue.size()while(size--){cur=queue.pop();for 结点 in cur的所有相邻结点:if 该节点有效且未被访问过:queue.push(该节点)}level++;
直接使用模板
算了dfs
class Solution {
public:int sum(int x){//计算数位和int count = 0;while(x){count += x%10;x /= 10;}return count;}int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//左上右下int res = 0;int m , n , k;vector<vector<bool>>st;int movingCount(int _m, int _n, int _k) {
//m行n列
//不能进入行坐标和列坐标的"数位"之和大于k的格子
// i + j > km = _m, n = _n, k = _k;vector<vector<bool>>_st(m,vector<bool>(n));//初始化st = _st;return dfs(0,0);}int dfs(int x, int y){st[x][y]=true;res++;for(int i = 0 ;i < 4 ; i++){int a = x+dx[i] , b = y + dy[i];if(a >= 0 && a < m && b >= 0 && b < n && !st[a][b] && sum(a)+sum(b)<=k){dfs(a,b);//那么我们就渲染一下}}return res;}};
DFS解法
class Solution {
public:int movingCount(int m, int n, int k) {vector<vector<int>> check(m,vector<int>(n,0));//球球你了祖宗啊记住这个定义方式吧dfs(check,m,n,k,0,0);return result;}private:int result=0;int add(int x){int sum=0,num=0;while(x){num=x%10;x=x/10;sum+=num;}return sum;}void dfs(vector<vector<int>> &check,int m, int n, int k,int x,int y){int sum=add(x)+add(y);if(x<0||x>=m||y<0||y>=n||check[x][y]==1||sum>k) return ;result++;check[x][y]=1;dfs(check,m,n,k,x+1,y);dfs(check,m,n,k,x,y+1);}
};
BFS解法就见鬼去吧 不想写队列啊啊啊啊
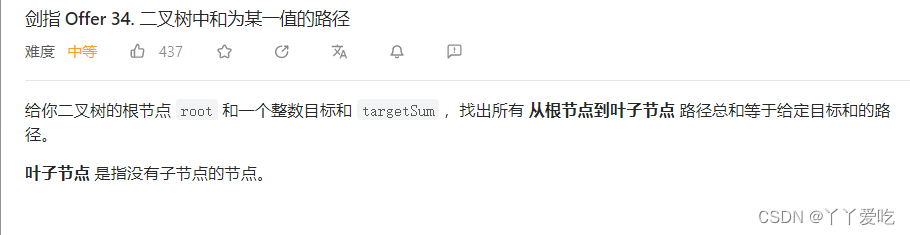
class Solution {
public:vector<vector<int>> pathSum(TreeNode* root, int target) {if(!root) return result;dfs(root,target);return result;}
private:vector<vector<int>> result;vector<int> subresult;void dfs(TreeNode* root,int target){if(!root) return ;subresult.push_back(root->val);target-=root->val;if(root->left==nullptr&&root->right==nullptr&&target==0){result.push_back(subresult);}dfs(root->left,target);dfs(root->right,target);subresult.pop_back();//回溯}
};
相关文章:

剑指offer12 矩阵中的路径 13 机器人的运动范围 34.二叉树中和为某一值得路径
class Solution { public:bool exist(vector<vector<char>>& board, string word) {int rowboard.size(),colboard[0].size();int index0,i0,j0;if(word.size()>row*col) return 0;//vector<vector<int>> visit[row][col];//标记当前位置有没有…...

Pushgateway+Prometheus监控Flink
思路方案 FlinkMtrics->pushgateway->prometheus->grafnana->altermanager 方案 : Flink任务先将数据推到pushgateway。然后pushgateway将值推送到prometheus,最后grafana展示prometheus中的值, 去这个 https://prometheus.io/download/ 下载最新的 Prometheu…...
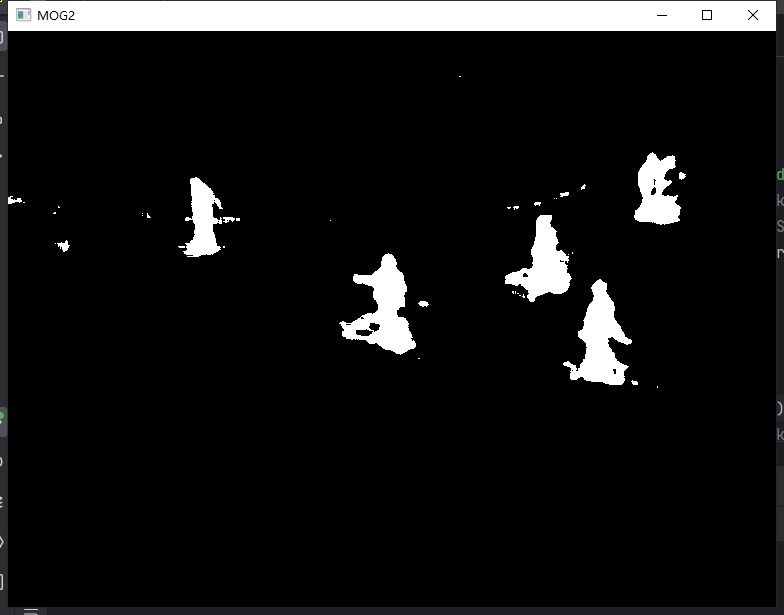
OpenCV图像处理-视频分割静态背景-MOG/MOG2/GMG
视频分割背景 1.概念介绍2. 函数介绍MOG算法MOG2算法GMG算法 原视频获取链接 1.概念介绍 视频背景扣除原理:视频是一组连续的帧(一幅幅图组成),帧与帧之间关系密切(GOP/group of picture),在GOP中,背景几乎…...

nginx 反向代理浅谈
前言 通常情况下,客户端向Web服务器发送请求,Web服务器响应请求并返回数据。而在反向代理中,客户端的请求不直接发送到Web服务器,而是发送到反向代理服务器。反向代理服务器会将请求转发给真实的Web服务器,Web服务器响…...
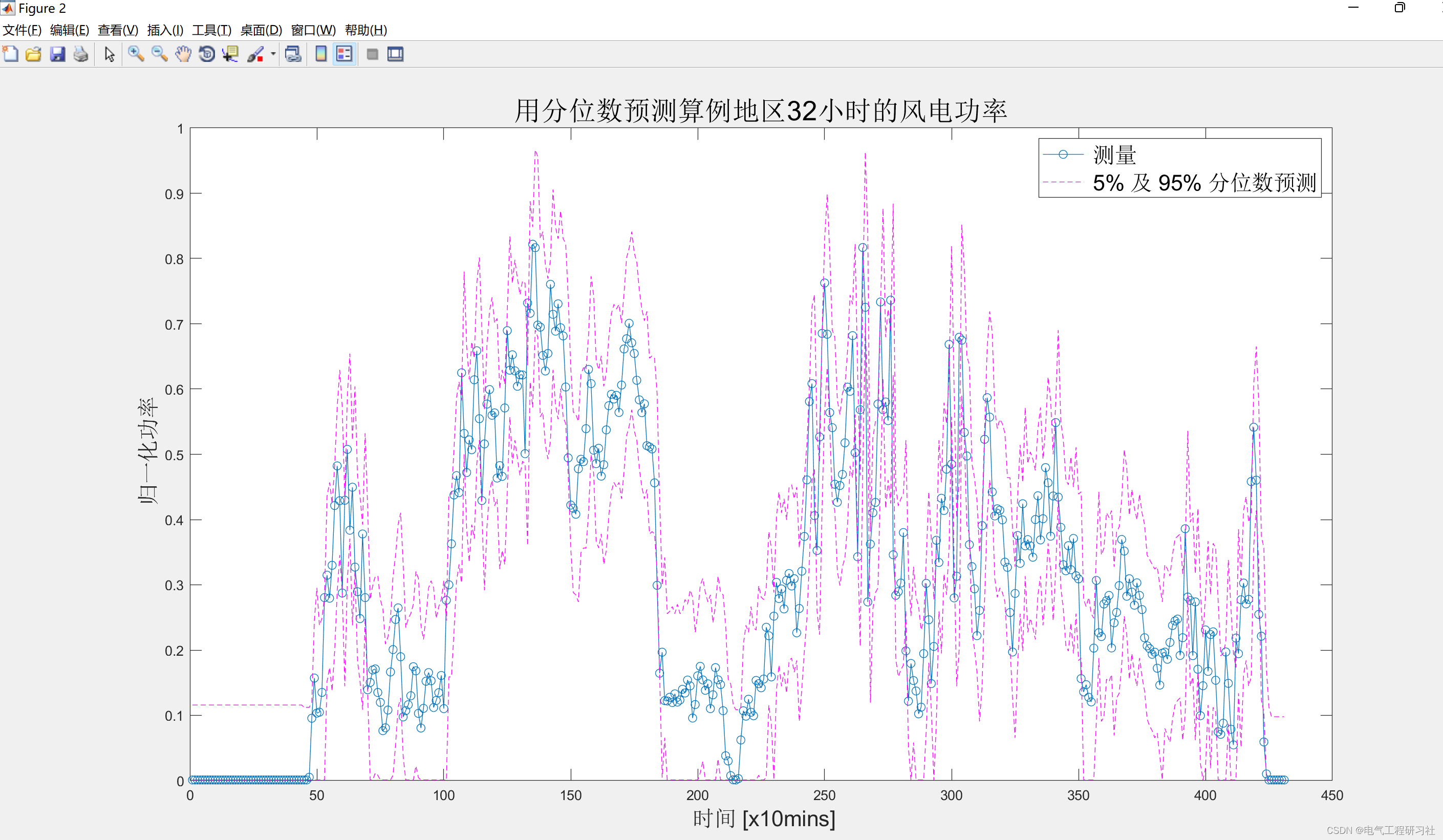
【概率预测】对风力发电进行短期概率预测的分析研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

原型设计模式go实现尝试
文章目录 前言代码结果总结 前言 本文章尝试使用go实现“原型”。 代码 package mainimport ("fmt" )// 不同原型标志枚举 type Type intconst (PROTOTYPE_1 Type iotaPROTOTYPE_2 )// 原型接口 type IPrototype interface {Clone() IPrototypeMethod(value int)P…...
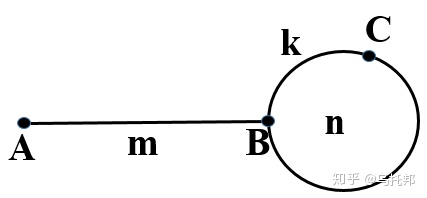
链表是否有环、环长度、环起点
问题引入 如何检测一个链表是否有环,如果有,那么如何确定环的长度及起点。 引自博客:上述问题是一个经典问题,经常会在面试中被问到。我之前在杭州一家网络公司的电话面试中就很不巧的问到,当时是第一次遇到那个问题&…...

有效文档管理离不开这几个特点
在我们日常生活中经常会遇到各式各样的文档类型,想要把它们都统一管理起来也不是一件容易的事情。后来looklook就去研究怎么样可以把这一堆文档整理起来呢?接下来,looklook就从有效的文档管理展开,和大家分享一下! 有效…...

爬虫-requests-cookie登录古诗文网
一、前言 1、requests简介 requests是一个很实用的Python HTTP客户端库,爬虫和测试服务器响应数据时经常会用到,它是python语言的第三方的库,专门用于发送HTTP请求,使用起来比urllib更简洁也更强大。 2、requests的安装 pip i…...
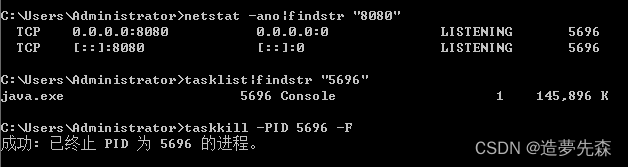
Spring Boot实践三 --数据库
一,使用JdbcTemplate访问MySQL数据库 1,确认本地已正确安装mysql 按【winr】快捷键打开运行;输入services.msc,点击【确定】;在打开的服务列表中查找mysql服务,如果没有mysql服务,说明本机没有…...
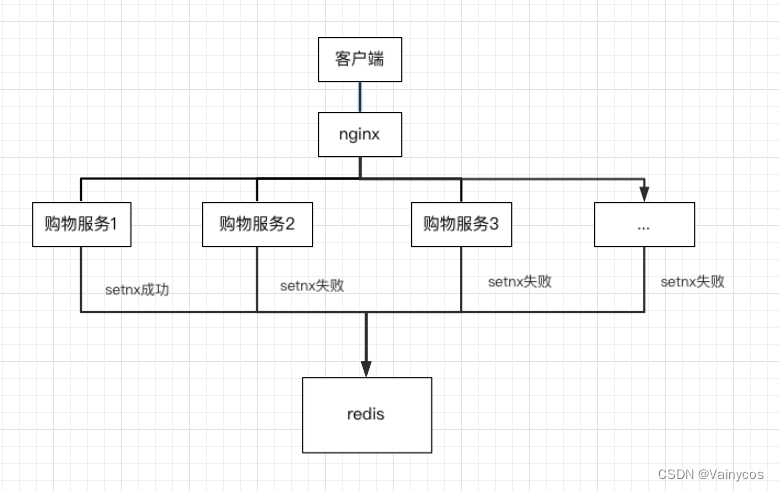
分布式锁漫谈
简单解释一下个人理解的分布式锁以及主要的实现手段。 文章目录 什么是分布式锁常用分布式锁实现 什么是分布式锁 以java应用举例,如果是单应用的情况下,我们通常使用synchronized或者lock进行线程锁,主要为了解决多线程或者高并发场景下的共…...
mac 安装 php 与 hyperf 框架依赖的扩展并启动 gptlink 项目
m系列 mac 安装 php 与 hyperf 框架依赖的扩展并启动 gptlink 项目 gptlink 项目是一个前后端一体化的 chatgpt 开源项目 gptlink 项目地址:https://github.com/gptlink/gptlink 安装 php 8.0 版本: brew install php8.0安装完成后提示如下ÿ…...

ansible中run_once的详细介绍和使用说明
在Ansible中,run_once是一个用于控制任务在主机组中只执行一次的关键字参数。当我们在编写Ansible任务时,有时候我们希望某个任务只在主机组中的某个主机上执行一次,而不是在每个主机上都执行。 以下是run_once参数的详细说明和用法…...
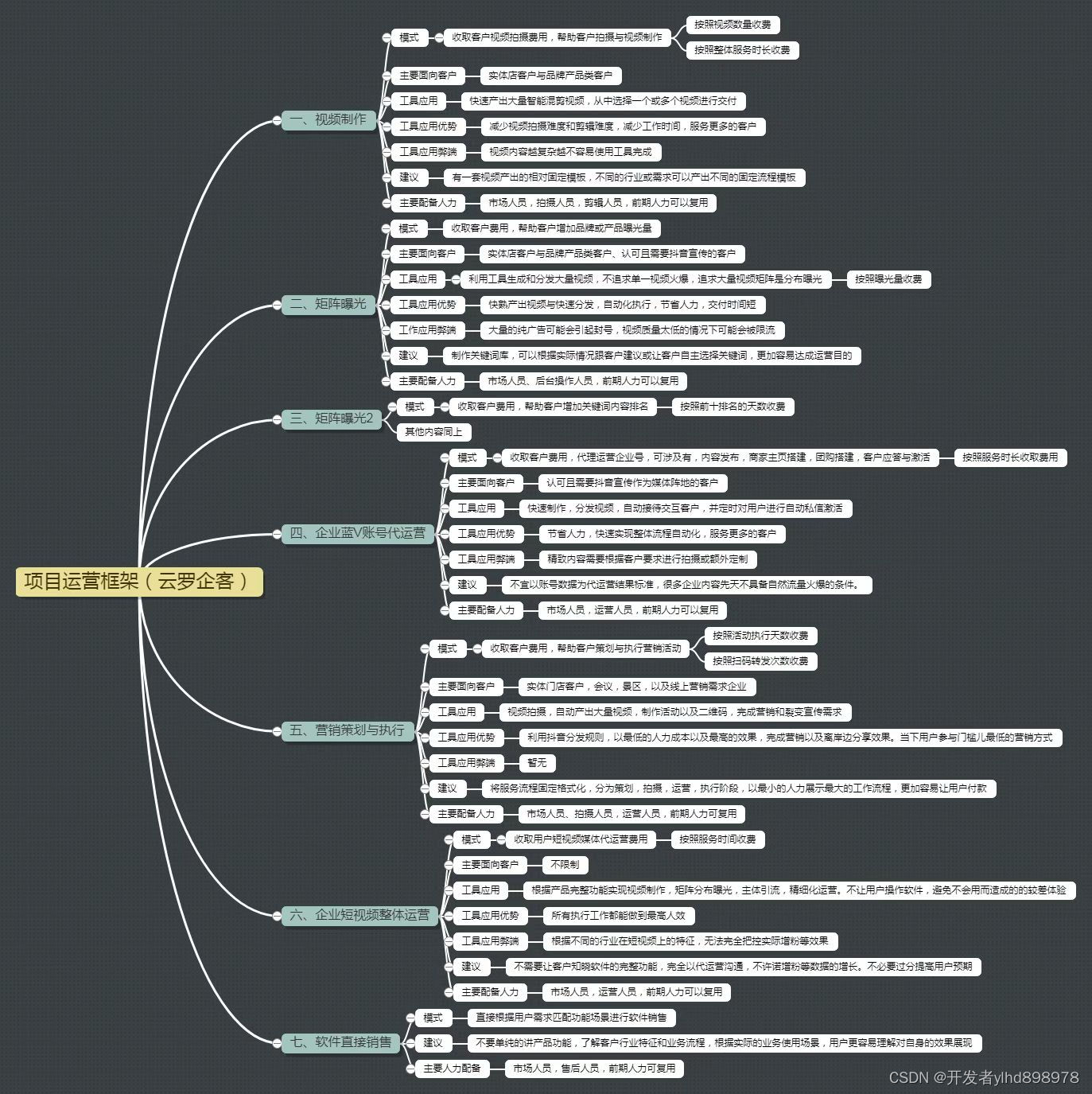
短视频矩阵系统源码开发流程
一、视频矩阵系统源码开发流程分为以下几个步骤: 四、技术开发说明: 产品原型PRD需求文档产品交互流程图部署方式说明完整源代码源码编译方式说明三方框架和SDK使用情况说明和代码位置平台操作文档程序架构文档 一、抖音SEO矩阵系统源码开发流程分为以…...

vite+vue3 css scss PC移动布局自适应
1. 安装 postcss-pxtorem 和 autoprefixer npm install postcss-pxtorem autoprefixer --save2. vite.config.js引入并配置 import postCssPxToRem from postcss-pxtorem import autoprefixer from autoprefixerexport default defineConfig({base: ./,resolve: {alias},plug…...

BLE配对和绑定
参考:一篇文章带你解读蓝牙配对绑定 参考:BLE安全之SM剖析(1) 参考:BLE安全之SM剖析(2) 参考:BLE安全之SM剖析(3) 目录 前言基本概念解读Paring(配对)Bonding(绑定)STK短期秘钥、LTK长期秘钥等 …...
方法函数)
无涯教程-jQuery - html( val )方法函数
html(val)方法设置每个匹配元素的html内容。此属性在XML文档上不可用。 html( val ) - 语法 selector.html( val ) 这是此方法使用的所有参数的描述- val - 这是要设置的html内容。 html( val ) - 示例 以下是一个简单的示例,简单说明了此方法的用法- <…...

【单链表OJ题:删除链表中等于给定值 val 的所有节点】
1.删除链表中等于给定值 val 的所有节点 题目来源 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 /*** Definition for singly-linked list.* struct ListNode {* int val;* s…...
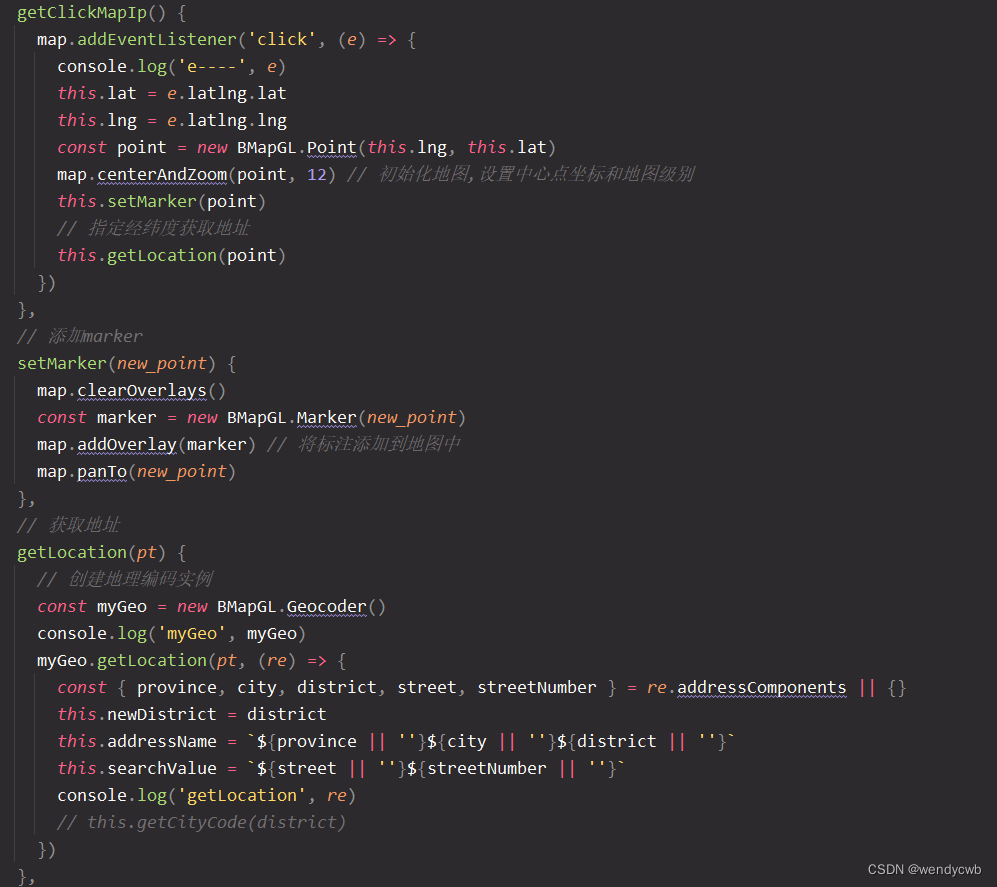
vue element ui web端引入百度地图,并获取经纬度
最近接到一个新需要,要求如下: 当我点击选择地址时,弹出百度地图, 效果如下图: 实现方法: 1、首先要在百度地图开放平台去申请一个账号和key 2、申请好之后,在项目的index.html中引入 3、…...

25.10 matlab里面的10中优化方法介绍—— 函数fmincon(matlab程序)
1.简述 关于非线性规划 非线性规划问题是指目标函数或者约束条件中包含非线性函数的规划问题。 前面我们学到的线性规划更多的是理想状况或者说只有在习题中,为了便于我们理解,引导我们进入规划模型的一种情况。相比之下,非线性规划会更加贴近…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
