无涯教程-jQuery - empty( )方法函数
empty()方法删除所有匹配的子节点。
empty( ) - 语法
selector.empty( )
empty( ) - 示例
以下是一个简单的示例，简单说明了此方法的用法-
<html><head><title>The jQuery Example</title><script type="text/javascript" src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.3/jquery.min.js"></script><script type="text/javascript" language="javascript">$(document).ready(function() {$("div").click(function () {$(this).empty();});});</script><style>.div{ margin:10px;padding:12px; border:2px solid #666; width:60px;}</style></head><body><p>Click on any square below to see the result:</p><div class="div" style="background-color:blue;">ONE</div><div class="div" style="background-color:green;">TWO</div><div class="div" style="background-color:red;">THREE</div></body> </html>
这将产生以下输出-
参考链接
https://www.learnfk.com/jquery/dom-empty.html
相关文章：
方法函数){kind=spacer}
无涯教程-jQuery - empty( )方法函数
empty()方法删除所有匹配的子节点。 empty( ) - 语法 selector.empty( ) empty( ) - 示例 以下是一个简单的示例，简单说明了此方法的用法- <html><head><title>The jQuery Example</title><script type"text/javascript"…...
微信小程序实现蓝牙开锁、开门、开关、指令发送成功，但蓝牙设备毫无反应、坑
文章目录 开源htmlJavaScript 开源 wx联系本人获取源码(开源): MJ682517 html <view><view class"p_l_36 p_r_36"><input class"w_100_ h_80 lh_80 ta_c b_2s_eee radius_20" value"{{instructVal}}" type"text" plac…...
微信小程序中使用echarts方法
小程序中使用echarts echarts是一个基于JS的数据可视化图标库，它提供了直观，生动，可交互，可个性定制的数据可视化图表。一般在vue中会使用到，并且官网也详细的说明了如何在vue中使用，但是今天我想来探讨的…...
【面试题】前端中 JS 发起的请求可以暂停吗？
这个问题非常有意思，我一看到就想了很多可以回复的答案，但是评论区太窄，就直接开一篇文章来写了。 审题 JS 发起的请求可以暂停吗？这一句话当中有两个概念需要明确，一是什么样的状态才能称之为 暂停？二是…...
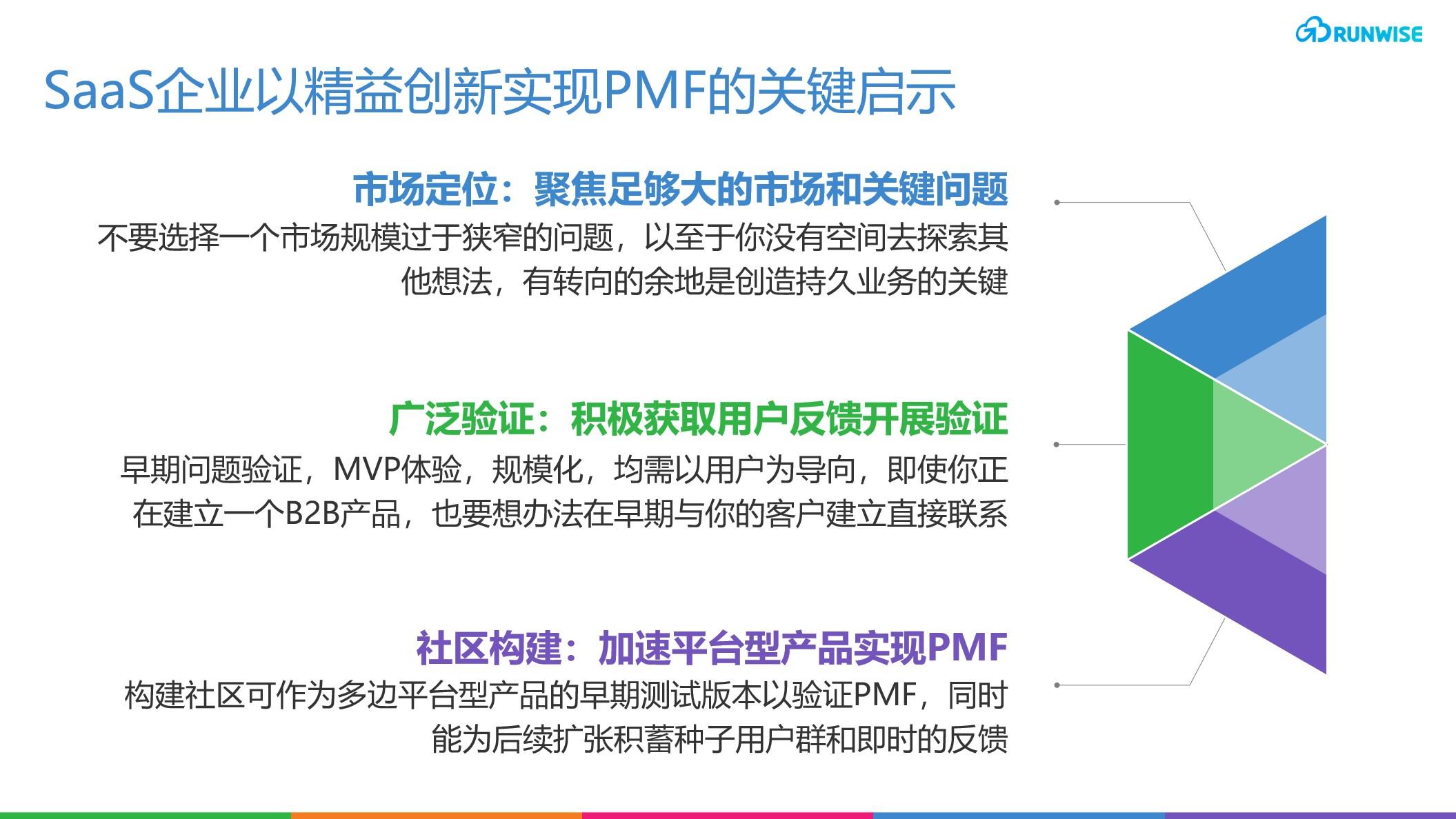
通过社区参与解锁早期增长：Maven 远程医疗平台概览
Maven通过用户导向的渐进式验证，找到了一个被忽视的巨大女性医疗服务市场，作为女性医疗保健的先行者，已服务超过1500万用户，目前估值已达$14亿。本文将深入探索Maven实现产品市场匹配的三个阶段，从如何验证初始的市场机…...
Vue中使用echarts
1 安装 npm install -g cnpm --registryhttps://registry.npm.taobao.org cnpm install echarts -S 2 main.js引入 3 引入成功...
边缘计算对现代交通的重要作用
边缘计算之所以重要，是在于即使在5G真正商用之时，可以实现超大带宽（eMBB）的应用场景，但庞大数据量的涌现也就意味着需要在云和端传输过程中找到一个承接点，对数据进行预处理再选择是否上云。 边缘计算应用演…...
Python桥接模式介绍、使用
一、Python桥接模式介绍 概念： Python桥接模式（Bridge Pattern）是一种软件设计模式，用于将抽象部分与其实现部分分离，使它们可以独立地变化。 它可以通过使用桥接接口来创建一个桥接对象来连接抽象和实现部分。 功能…...
ChatGPT在知识图谱的构建和更新中的应用如何？
ChatGPT在知识图谱的构建和更新中具有重要的应用潜力。知识图谱是一种用于表示和存储结构化知识的图形化数据模型，通常由实体、属性和关系组成。知识图谱的构建和更新是一个复杂而关键的过程，涉及知识的收集、组织、链接和推理。ChatGPT作为一种预训练语…...
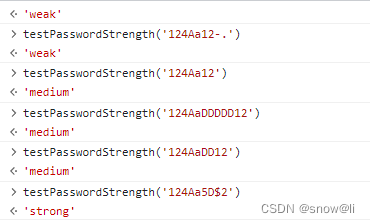
JS正则表达式：常用正则手册/RegExp/正则积累
一、正则基础语法 JavaScript 正则表达式 | 菜鸟教程 JS正则表达式语法大全（非常详细） 二、使用场景 2.1、校验中国大陆手机号的正则表达式 正则 /^1[3456789]\d{9}$/解释 序号正则解释1^1以数字 1 开头2[3456789]第二位可以是 3、4、5、6、7、8、…...
自动化测试框架unittest与pytest的区别！
引言 前面文章已经介绍了python单元测试框架，大家平时经常使用的是unittest，因为它比较基础，并且可以进行二次开发，如果你的开发水平很高，集成开发自动化测试平台也是可以的。而这篇文章主要讲unittest与pytest的区别&…...
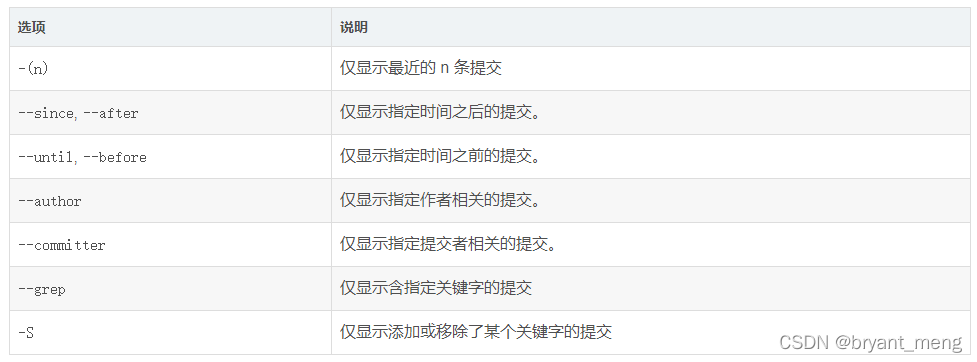
【Git】
学习来自于： 女朋友乱用Git，差点把我代码删了。。。 一些常用的Git 知识点整理 关于Git这一篇就够了 Git基本命令大全 30分钟精通Git，学不会来找我 Git 版本管理 | 莫烦PYTHON Git 代码版本管理教程 文章目录 【前言】集中式与分布式的…...
[论文笔记] CLRerNet: Improving Confidence of Lane Detection with LaneIoU
Honda, Hiroto, and Yusuke Uchida. “CLRerNet: Improving Confidence of Lane Detection with LaneIoU.” arXiv preprint arXiv:2305.08366 (2023). 2023.05 出的一篇车道线检测的文章, 效果在CULane, CurveLanes SOTA 文章目录 简介LaneIoULineIoU存在问题为什么使用LaneIo…...
LeetCode｜backtracking｜review：40. 131. 93. 47. 332. | 37. Sudoku Solver
复习： 40. Combination Sum II [1,1,2,3]中，答案里有[1,1,2], 但是不能有两个[1,2,3] 131. Palindrome Partitioning 每个for都是在给定的start之后找一个palindrome。当start 93. Restore IP Addresses forloop每次loop都是在给定的start的后三个数…...
被泼冷水后，谁能超越微服务？
历史总会重演。一切刚过去的，又会被重新提起。开源项目Codename One的联合创始人Shai，曾是Sun Microsystems开源LWUIT项目的共同作者，参与了无数开源项目。作为最早一批Java开发者，最近感慨道：单体，又回来了…...
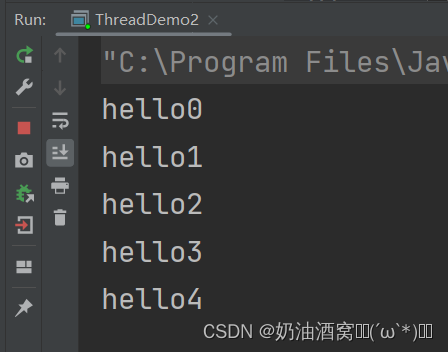
多线程（JavaEE初阶系列5）
目录 前言： 1.什么是定时器 2.标准库中的定时器及使用 3.实现定时器 结束语： 前言： 在上一节中小编给大家介绍了多线程中的两个设计模式，单例模式和阻塞式队列模式，在单例模式中又有两种实现方式一种是懒汉模式&a…...
Minimum Snap闭式求解相关公式推导
文章目录 1 M i n i m u m Minimum Minimum S n a p Snap Snap闭式求解的推导1.1 二次规划等式约束构建1.2 求 d d d1.3 转成无约束优化问题 1 M i n i m u m Minimum Minimum S n a p Snap Snap闭式求解的推导 可以看看我的这几篇Blog1，Blog2，Blog…...
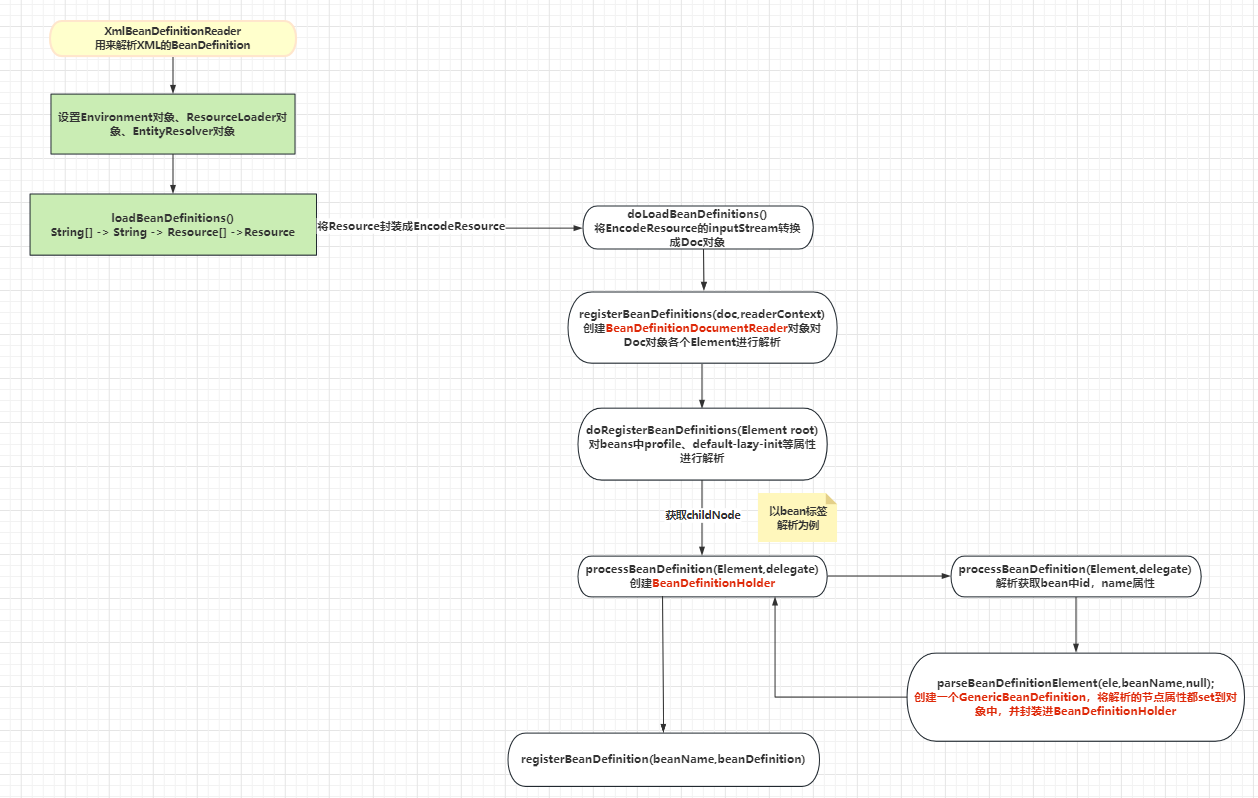
Spring源码（五）— 解析XML配置文件(一) bean标签解析流程
前面几章的内容已经介绍了BeanFactory创建前的准备工作，以及加载XML配置文件前的准备的步骤。本章会着重介绍解析XML的步骤。 registerBeanDefinitions 前几个方法不做过多的赘述，着重看registerBeanDefinitions方法中解析XML的步骤。 public int regi…...
隐私政策声明
http://lxfamn.cn/tools 我们注重对您个人隐私的保护。有时候我们需要某些信息才能为您提供您请求的服务，本隐私声明解释了这些情况下的数据收集和使用情况。本隐私声明适用于本网站的所有相关服务。如果您访问本网站、使用本网站的任何服务，那么您便接受…...
Flutter 最佳实践和编码准则
Flutter 最佳实践和编码准则 视频 前言 最佳实践是一套既定的准则，可以提高代码质量、可读性和可靠性。它们确保遵循行业标准，鼓励一致性，并促进开发人员之间的合作。通过遵循最佳实践，代码变得更容易理解、修改和调试ÿ…...
Python爬虫实战：研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库，专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力，提供了直观的 API，让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...
【Oracle APEX开发小技巧12】
有如下需求： 有一个问题反馈页面，要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据，方便管理员及时处理反馈。 我的方法：直接将逻辑写在SQL中，这样可以直接在页面展示 完整代码： SELECTSF.FE…...
java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中，我们会遇到使用 java 调用 dll文件 的情况，此时大概率出现UnsatisfiedLinkError链接错误，原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用，结果 dll 未实现 JNI 协…...
大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 （1）设置网关 打开VMware虚拟机，点击编辑…...
Android Bitmap治理全解析：从加载优化到泄漏防控的全生命周期管理
引言 Bitmap（位图）是Android应用内存占用的“头号杀手”。一张1080P（1920x1080）的图片以ARGB_8888格式加载时，内存占用高达8MB（192010804字节）。据统计，超过60%的应用OOM崩溃与Bitm…...
Redis的发布订阅模式与专业的 MQ（如 Kafka, RabbitMQ）相比，优缺点是什么？适用于哪些场景？
Redis 的发布订阅（Pub/Sub）模式与专业的 MQ（Message Queue）如 Kafka、RabbitMQ 进行比较，核心的权衡点在于：简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
【VLNs篇】07：NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战，克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了，就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
jdbc查询mysql数据库时，出现id顺序错误的情况
我在repository中的查询语句如下所示，即传入一个List<intager>的数据，返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致，会导致返回的id是从小到大排列的，但我不希望这样。 Query("SELECT NEW com…...