2020/7/30
Educational Codeforces Round 143 (Rated for Div. 2)\C_Tea_Tasting.cpp
//题意:有n种茶,n个人,第i种茶有 a[i]的量,第i个人一次能喝 b[i], 第i个人从第i种茶开始往前喝,求每个人最多能喝多少茶。
//思路:纯模拟时间超限,对于a数组中的每个元素,他要减的是包括i在内以及其右边的b数组中的元素,
//那么需要先求出b数组的前缀和数组sum,那么对于任意的ai,我们可以找到它从i向右减b中元素后第一次减成0的位置
//也就是在前缀和数组中从i向右的位置二分查找第一个sum[j]-sum[i-1]>ai的位置j,从i到j-1的每一个b中元素都是使ai减去一个完整的自己的,
//bj使ai减剩下的数减到了0,用差分数组cnt记录b中每个元素使a中元素减去了几个完整的自己也就是对于每次二分查找,都有cnt[i]++,cnt[j]--,
//然后用另一个数组ex记录b中每个数使a中某个数减到零所提供的贡献,n次二分查找结束后,对差分数组求前缀和,答案数组就等于cnt[i]*b[i]+ex[i]
#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;int n,m;int a[N];int b[N];int sum[N];int ex[N];void solve(){/* cin>>n;fr(i,1,n){cin>>a[i];c[i]=0;}fr(i,1,n){cin>>b[i];}fr(i,1,n){ufr(j,i,1){c[i]+=min(a[j],b[i]);if(b[i]>=a[j]){a[j]=0;}else{a[j]-=b[i];}}}fr(i,1,n){cout<<c[i]<<' ';}cout<<'\n'; */int n;cin>>n;fr(i,1,n){cin>>a[i];sum[i]=0;ex[i]=0;}fr(i,1,n){int x;cin>>x;b[i]=b[i-1]+x;}fr(i,1,n){int it=upper_bound(b+1,b+1+n,b[i-1]+a[i])-b; //后面的a不用减前面的b,整体基础上+b[i-1]//cout<<it<<' ';sum[i]++;sum[it]--;ex[it]+=a[i]-(b[it-1]-b[i-1]);}//cout<<'\n';fr(i,1,n){sum[i]+=sum[i-1];}fr(i,1,n){cout<<sum[i]*(b[i]-b[i-1])+ex[i]<<' ';}cout<<'\n';}signed main(){int t=1;cin>>t;while(t--) solve();return 0;}Codeforces Round 887 (Div. 2)\C_Ntarsis_Set.cpp
//题意:n个数,每次按照顺序删除位于a[i]位置的这n个数,问k次后最小的是多少
//思路:如果没有1,则最小为1,有1通过列举情况可以发现对于某一个删除位,前面有几个删除位,后面就要跳几次删,
//于是发现这是一个公差为1,2,3...不断变化的n个数列,第i个数列截止与a[i+1],为了防止没有k个数,于是增加一个公差为n+1,截止于1e18的数列
#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;int a[N];void solve(){int n,k;cin>>n>>k;fr(i,1,n){cin>>a[i];}if(a[1]!=1){cout<<1<<'\n';return;}a[n+1]=inf; //保证一定有k个数vector<int>v;int cnt=1;int d=1;fr(i,2,n+1){while(cnt+d<a[i]){cnt+=d;v.push_back(cnt);if(v.size()>k+1){break;}}if(v.size()>k+1){break;}d=i;}cout<<v[k-1]<<'\n';}signed main(){int t=1;cin>>t;while(t--) solve();return 0;}\Codeforces Round 842 (Div. 2)\C_Elemental_Decompress.cpp
//题意:给定一个长度为n的排列a,请构造两个数组 p,q,要求 max(pi,qi)=ai,并且两个数组都是排列,请输出两个数组。
//思路:1.对于出现三次及以上的NO,对于出现两次的一定有没出现出现的与之对应,否则NO
//2.将出现两次的与没出现的对应,没出现的记录,在记录寻找首次小于出现两次的对应,下一次再出现颠倒位置,
#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;int n,m;int a[N];int ans1[N];int ans2[N];void solve(){cin >> n;for (int i = 1; i <= n; i++ ) cin >> a[i];map<int, int> mp, st;for (int i = 1; i <= n; i++ ) {mp[a[i]]++ ;if(mp[a[i]] > 2){cout<<"NO"<<'\n';return ;}}int cur = 0;vector<int> v;for (int i = 1; i <= n; i++ ) {cur += mp[i];if(!mp[i]) v.push_back(i);if(cur > i){cout<<"NO"<<'\n';return;}}cout << "YES" << endl;for (int i = 1; i <= n; i++ ) {if(mp[a[i]] == 1) {ans1[i] = a[i];ans2[i] = a[i];continue;}if(!st[a[i]]) {auto it = lower_bound(v.begin(), v.end(), a[i]);if(it == v.begin()) { //没有小的cout<<"NO"<<'\n';return ;}it-- ;ans1[i] = *it;st[a[i]] = ans1[i];ans2[i] = a[i];v.erase(it); //还要删除防止重复} else {ans1[i] = a[i];ans2[i] = st[a[i]];}}for (int i = 1; i <= n; i++ )cout << ans1[i] << " \n"[i == n];for (int i = 1; i <= n; i++ )cout << ans2[i] << " \n"[i == n];}signed main(){int t=1;cin>>t;while(t--) solve();return 0;}相关文章:

2020/7/30
Educational Codeforces Round 143 (Rated for Div. 2)\C_Tea_Tasting.cpp //题意:有n种茶,n个人,第i种茶有 a[i]的量,第i个人一次能喝 b[i], 第i个人从第i种茶开始往前喝,求每个人最多能喝多少茶。 //思路ÿ…...
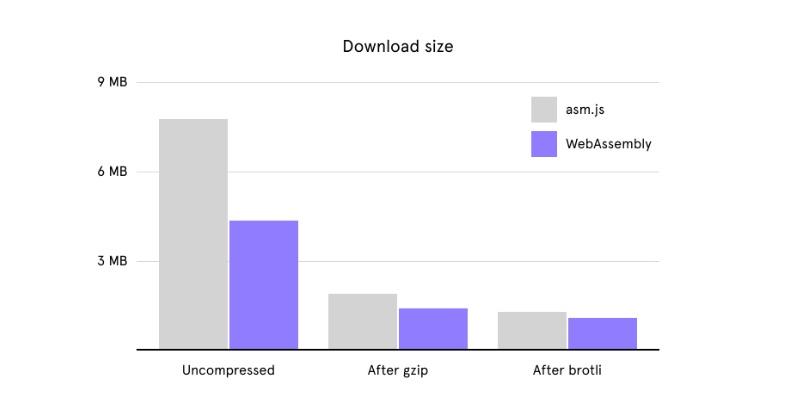
图形编辑器开发:是否要像 Figma 一样上 wasm
大家好,我是前端西瓜哥。 wasm 拿来做 Web 端的图形编辑器貌似是不错的选择。 因为图形处理会有相当多无法利用到 WebGL GPU 加速的 CPU 密集的计算。比如对一条复杂贝塞尔曲线进行三角化,对多个图形进行复杂图形的布尔运算。 图形编辑器性能天花板 F…...

Linux学成之路(基础篇0(二十三)MySQL服务(主从MySQL服务和读写分离——补充)
目录 一、MySQL Replication概述 优点 异步复制(Asynchronous repication) 全同步复制(Fully synchronous replication) 半同步复制(Semisynchronous replication) 三、MySQL支持的复制 四、部署主从…...

spring启动流程 (6完结) springmvc启动流程
SpringMVC的启动入口在SpringServletContainerInitializer类,它是ServletContainerInitializer实现类(Servlet3.0新特性)。在实现方法中使用WebApplicationInitializer创建ApplicationContext、创建注册DispatcherServlet、初始化ApplicationContext等。 SpringMVC…...

设计模式-中介者模式在Java中使用示例-客户信息管理
场景 欲开发客户信息管理窗口界面,界面组件之间存在较为复杂的交互关系:如果删除一个客户, 要在客户列表(List)中删掉对应的项,客户选择组合框(ComboBox)中客户名称也将减少一个; 如果增加一个客户信息,…...

14443-1-doc
介绍 ISO/IEC 14443 是描述 ISO/IEC 7810 中定义的身份证参数以及此类卡在国际交换中的使用的一系列国际标准之一。 ISO/IEC 14443 的这一部分描述了感应卡的物理特性。 ISO/IEC 14443 的这一部分并不排除在卡上纳入其他标准技术,例如资料性附录 A 中引用的技术。非…...
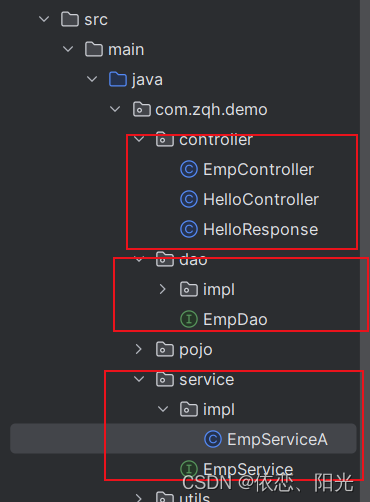
SpringBoot的三层架构以及IOCDI
目录 一、IOC&DI入门 二、三层架构 数据库访问层 业务逻辑层 控制层 一、IOC&DI入门 在软件开发中,IOC(Inversion of Control)和DI(Dependency Injection)是密切相关的概念。 IOC(控制反转&a…...
RabbitMQ部署指南
RabbitMQ部署指南 1.单机部署 我们在Centos7虚拟机中使用Docker来安装。 1.1.下载镜像 方式一:在线拉取 docker pull rabbitmq:3-management方式二:从本地加载 已经提供了镜像包: 上传到虚拟机中后,使用命令加载镜像即可&…...
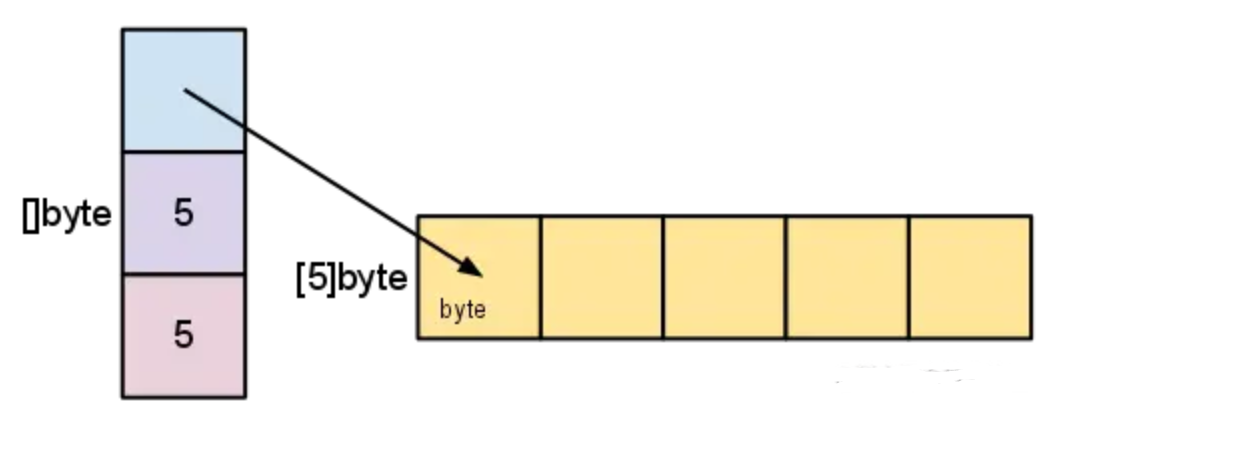
【Golang】Golang进阶系列教程--Go 语言切片是如何扩容的?
文章目录 前言声明和初始化扩容时机源码分析go1.17go1.18内存对齐 总结 前言 在 Go 语言中,有一个很常用的数据结构,那就是切片(Slice)。 切片是一个拥有相同类型元素的可变长度的序列,它是基于数组类型做的一层封装…...
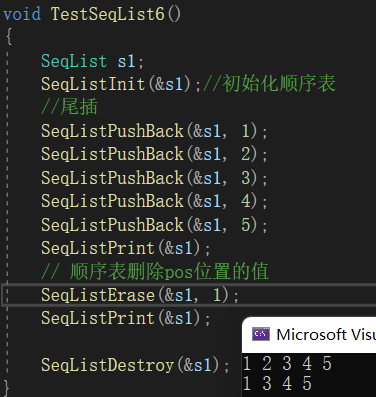
【数据结构】顺序表(SeqList)(增、删、查、改)详解
一、顺序表的概念和结构 1、顺序表的概念: 顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存储。在数组上完成数据的增删查改。 2、顺序表的结构: (1)静态顺序表:使…...

[golang gin框架] 42.Gin商城项目-微服务实战之后台Rbac微服务角色增删改查微服务
一.重构后台Rbac用户登录微服务功能 上一节讲解了后台Rbac微服务用户登录功能以及Gorm数据库配置单独抽离,Consul配置单独抽离,这一节讲解后台Rbac微服务角色增删改查微服务功能,Rbac微服务角色增删改查微服务和后台Rbac用户登录微服务是属于…...
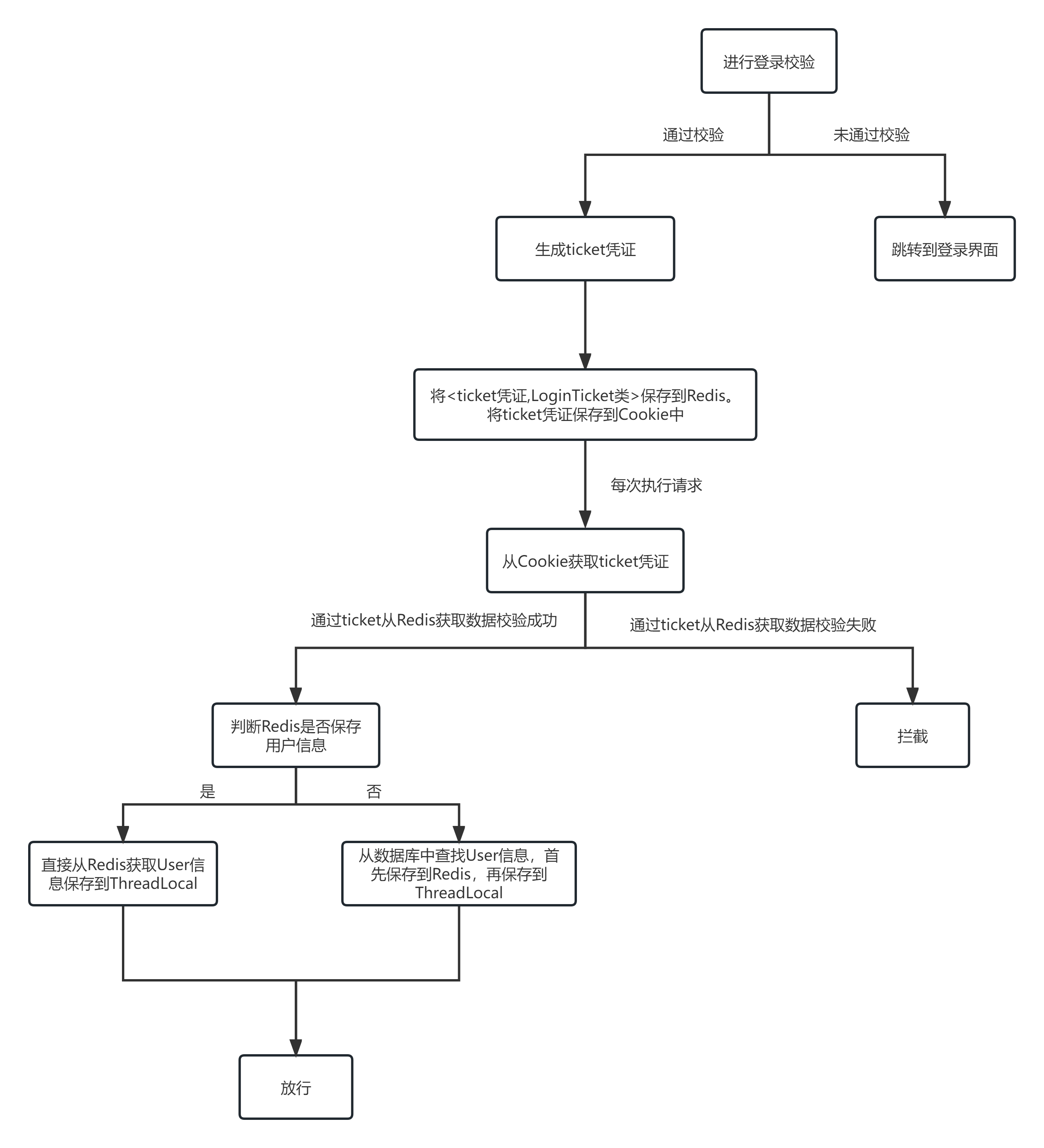
项目篇:Echo论坛系统项目
一、登录注册模块 1、注册功能 1.1、注册流程图 1.2、注册代码 /*** 用户注册* param user* return Map<String, Object> 返回错误提示消息,如果返回的 map 为空,则说明注册成功*/public Map<String, Object> register(User user) {Map&l…...
数据可视化(2)
1.柱状图 #柱状图 #bar(x,height,width,*,aligncenter,**kwargs) #height柱子的高度,即y轴上的数据 #width数组的宽度,默认值0.8 #*表示后面的参数为匿名关键字,必须传入参数 #kwargs关键字参数x[1,2,3,4,5] height[random.randint(10,100)f…...
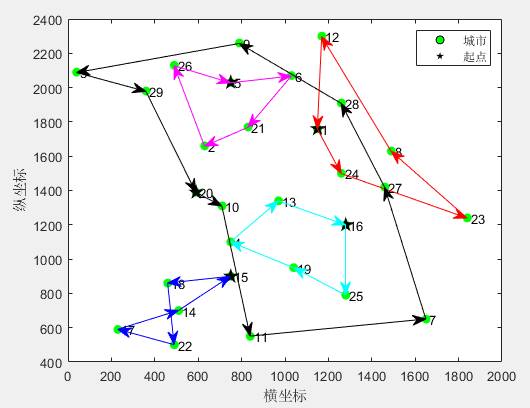
MD-MTSP:斑马优化算法ZOA求解多仓库多旅行商问题MATLAB(可更改数据集,旅行商的数量和起点)
一、斑马优化算法ZOA 斑马优化算法(Zebra Optimization Algorithm,ZOA)Eva Trojovsk等人于2022年提出,其模拟斑马的觅食和对捕食者攻击的防御行为。斑马优化算法(Zebra Optimization Algorithm,ZOA&#x…...

【笔试强训选择题】Day32.习题(错题)解析
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:笔试强训选择题 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!! 文章目录 前言 一、Da…...
抖音seo账号矩阵系统源码如何开发布局?
目录 一、 抖音SEO账号矩阵系统源码的开发布局步骤如下: 二。 开发部署源码 三、 开发部署功能设计 1. 短视频AI智能创作 2. 托管式账号管理: 3. 数据分析 4. 智能营销获客 四。 抖音seo源码开发部署交付技术文档包含 五。 开发代码展示: 一、 抖…...

vue项目cdn打包优化
0.用vue ui可以查看项目打包后的情况。 1.定义包的排除 let externals {axios: axios,element-ui: ELEMENT,echarts: echarts,} configureWebpack: {externals: externals }2.配置cdn包资源 // 配置 let cdn {css: [// element-ui csshttps://unpkg.com/element-ui/lib/th…...

Android 之 MediaPlayer 播放音频与视频
本节引言: 本节带来的是Android多媒体中的——MediaPlayer,我们可以通过这个API来播放音频和视频 该类是Androd多媒体框架中的一个重要组件,通过该类,我们可以以最小的步骤来获取,解码 和播放音视频。它支持三种不同的…...

React中事件处理器的基本使用
在React中,为了提高性能,跨浏览器兼容性和开发体验,React实现了一套自己的事件机制,利用事件委托和合成事件的方式统一管理事件订阅和分发。 为了让组件能够响应用户的交互行为,React提供了一系列的事件处理器…...

RobotFramework
一、RobotFramework的简介和特点 1、关键字驱动: 把项目中的业务逻辑封装成一个一个的关键字,然后调用不同的关键字组成不同的业务 2、数据驱动 把测试数据放到excel:yaml文件中 通过改变文件中的数据去驱动测试用例执行 3、特点ÿ…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
