matlab使用教程(5)—矩阵定义和基本运算
1创建矩阵
A = pascal(3)B = magic(3)C = randi(10,3,2)u = [3; 1; 4]
v = [2 0 -1]
s = 72矩阵的加法和减法
X = A + B
Y = X - A3向量乘积和转置
u = [3; 1; 4];
v = [2 0 -1];
x = v*uX = u*vB = magic(3)X = B'x = v'z = [1+2i 7-3i 3+4i; 6-2i 9i 4+7i]z'z.'4矩阵乘法
A = pascal(3);
B = magic(3);
m = 3;
n = 3;
for i = 1:m
for j = 1:n
C(i,j) = A(i,:)*B(:,j);
end
endX = A*B
Y = B*Au = [3; 1; 4];
x = A*u
v = [2 0 -1];
y = v*BX = A*CY = C*As = 10;
w = s*y5单位矩阵
eye(m,n)6矩阵求逆
A = pascal(3)X = inv(A)A*Xd = det(A)c = cond(A)7向量范数和矩阵范数

v = [2 0 -1];
[norm(v,1) norm(v) norm(v,inf)]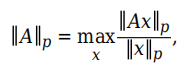
A = pascal(3);
[norm(A,1) norm(A) norm(A,inf)]vecnorm(A)8使用线性代数方程函数的多线程计算
相关文章:
matlab使用教程(5)—矩阵定义和基本运算
本博客介绍如何在 MATLAB 中创建矩阵和执行基本矩阵计算。 MATLAB 环境使用矩阵来表示包含以二维网格排列的实数或复数的变量。更广泛而言,数组为向量、矩阵或更高维度的数值网格。MATLAB 中的所有数组都是矩形,在这种意义上沿任何维度的分量向量的长度…...

用HTML写一个简单的静态购物网站
实现代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>购物网站</title> &l…...

如何在go中实现程序的优雅退出,go-kratos源码解析
使用kratos这个框架有近一年了,最近了解了一下kratos关于程序优雅退出的具体实现。 这部分逻辑在app.go文件中,在main中,找到app.Run方法,点进入就可以了 它包含以下几个部分: App结构体:包含应用程序的配置选项和运行时状态。 …...

Appium+python自动化(二十八)- 高级滑动(超详解)
高级溜冰的滑动 滑动操作一般是两点之间的滑动,这种滑动在这里称其为低级的溜冰滑动;就是上一节给小伙伴们分享的。然而实际使用过程中用户可能要进行一些多点连续滑动操作。如九宫格滑动操作,连续拖动图片移动等场景。那么这种高级绚丽的溜…...
github token使用方法
git remote set-url origin https://<githubtoken>github.com/<username>/<repositoryname>.git 在私有仓库的HTTPS的url上加入<githubtoken>即为token url,可以免ssh key登录...

Spring属性注解对配置项名称的自动转换
一、前言 在Spring中,我们经常需要将配置文件中的属性值注入到Java类中。Spring提供了两个主要的注解来实现这一功能:Value 和 ConfigurationProperties。其中 ConfigurationProperties支持将配置项名称与Java类中的属性名进行自动转换,包括…...
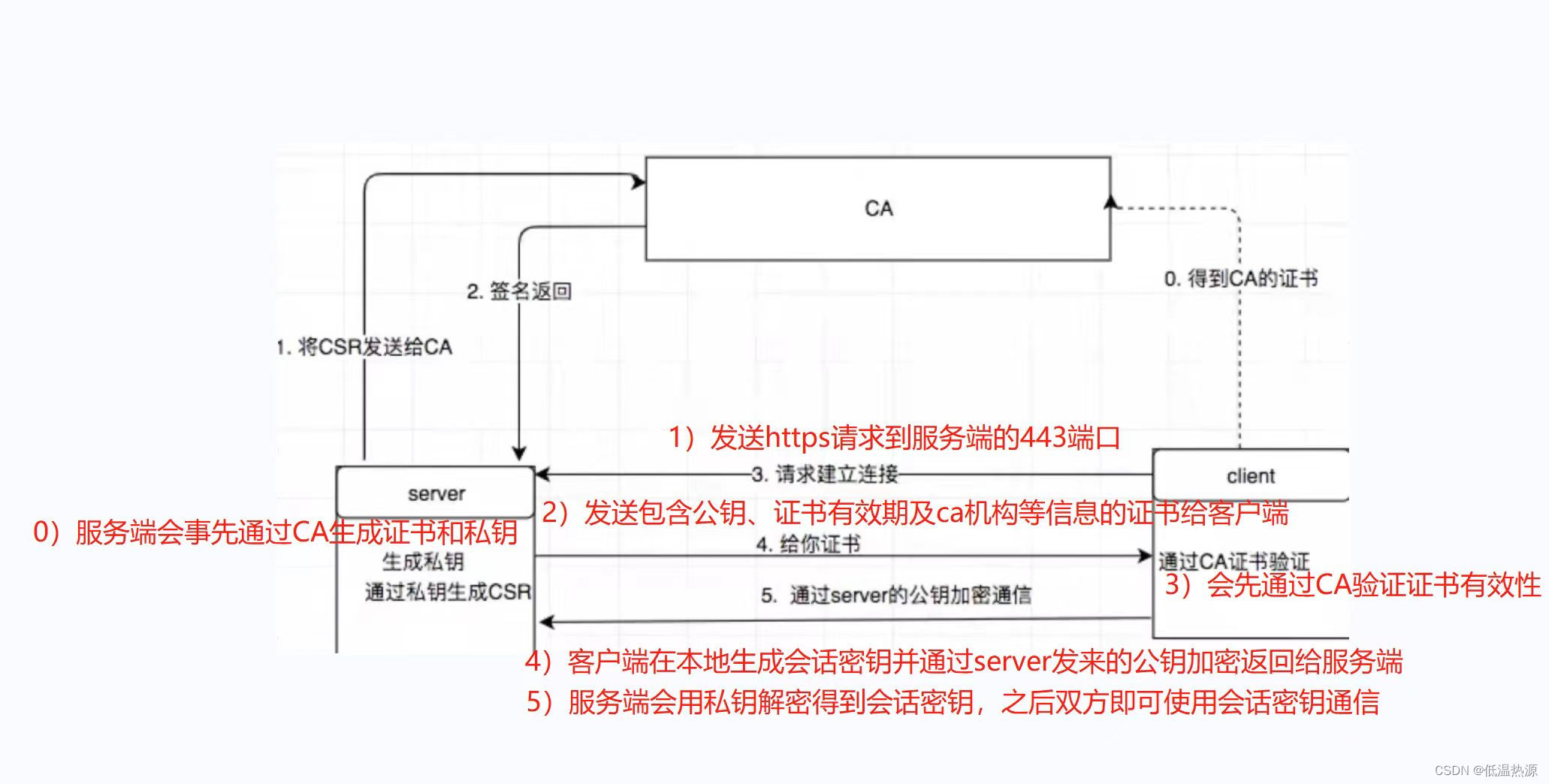
Docker 安全 Docker HTTPS请求过程与配置
Docker 容器安全注意点 尽量别做的事 尽量不用 --privileged 运行容器(授权容器root用户拥有宿主机的root权限) 尽量不用 --network host 运行容器(使用 host 网络模式共享宿主机的网络命名空间) 尽量不在容器中运行 ssh 服务 尽…...
DevOps(三)
CD(二) 1. 整体流程2. 环境准备1. jenkins安装2. 编译安装git3. docker安装4. docker-compose安装5. sonarqube安装6. harbor安装7. gitlab私服8. maven安装9. Nexus部署10. K8s部署3. 安装java及编写代码3.1 安装java3.2 安装IntelliJ IDEA3.3 安装tomcat3.4 安装maven3.5 c…...

AOP的妙用
一、改代码 自定义注解用于提示该代码已经在AOP中重构了 public interface ReviseToAop {// 用于记录修改状态String value() default ""; }使用注解(无意义,只是表名被修改) ReviseToAop("修改于:2023/7/30&quo…...
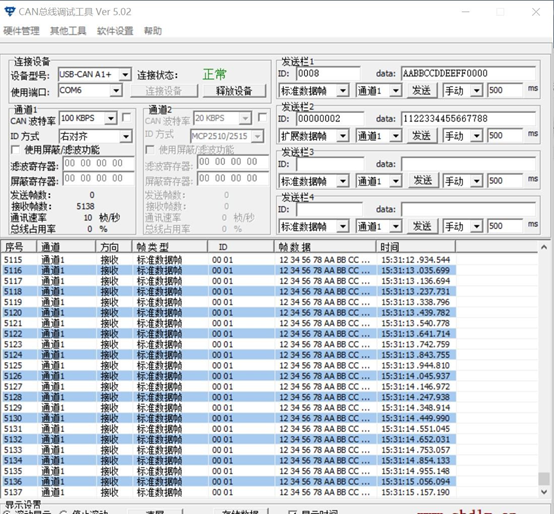
CAN转ETHERCAT网关将CAN 总线和 ETHERCAT 网络连接方法
由于好多现场会出现将CAN总线的设备接到EtherCAT网络中,由于协议的不相同,不能直接进行连接,现需一种能同时兼容CAN 总线和ETHERCAT网络的一种设备,由此捷米JM-ECT-CAN 是自主研发的一款 ETHERCAT 从站功能的通讯网关。该产品主要…...
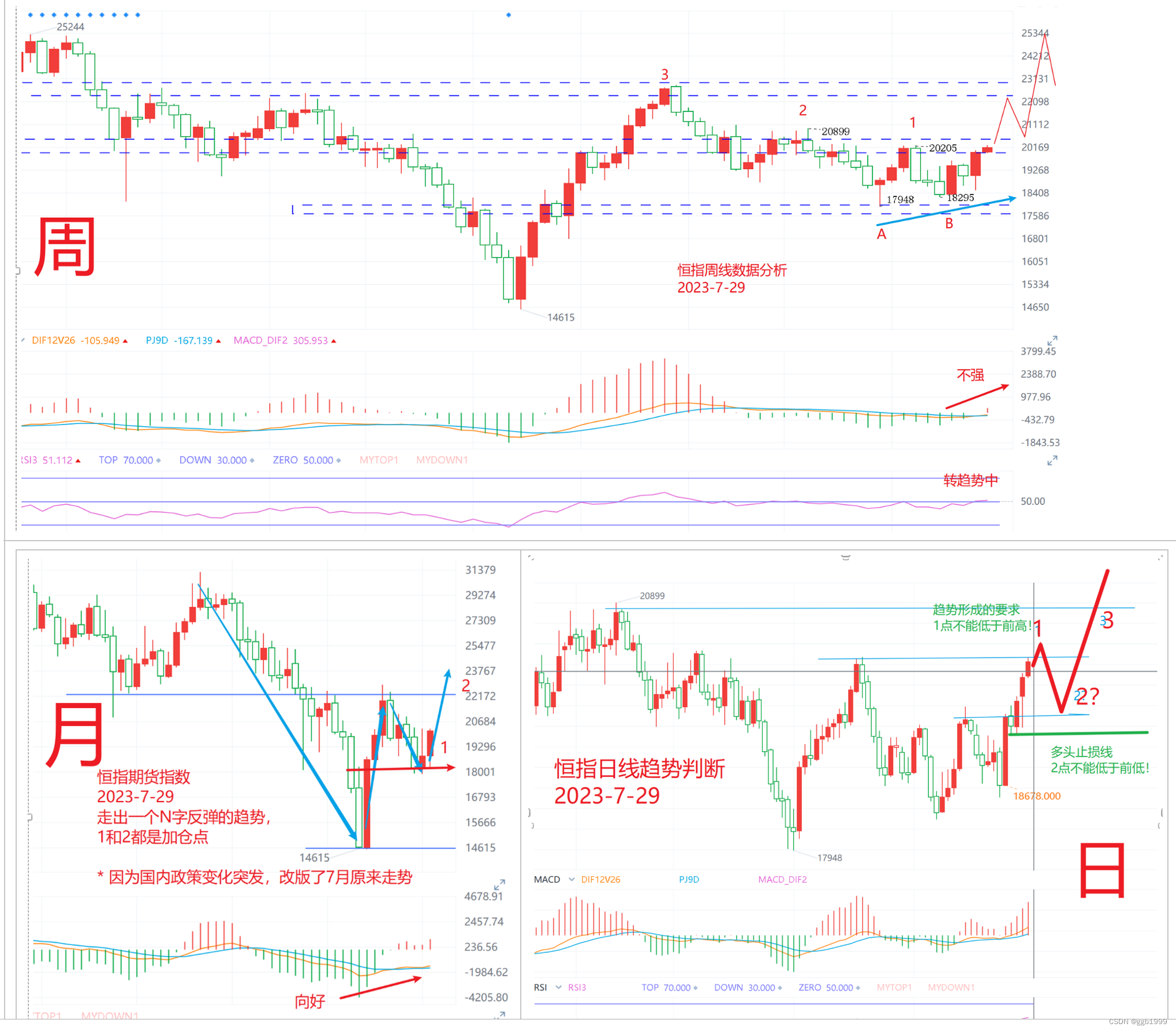
【大数据趋势】7月30日 汇率,恒指期货的大数据趋势概率分析。
1. 数据源头之一 : 汇率变化 从程序模拟趋势来看,美元在持续弱势状态,周线上正在构建一个新的下跌趋势,而且正在反抽过程中,即将完成,如果没有外部干预,会顺势往下。从月线来看,高点逐步降低&a…...
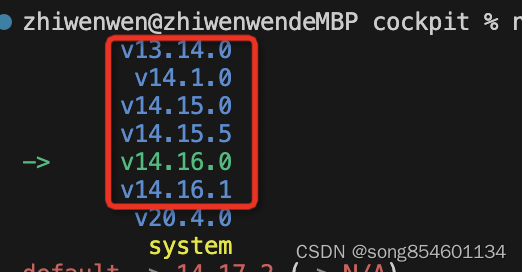
mac使用mvn下载node-sass 会Binary download failed, trying source
m1 上使用nvm 以下node的版本可以直接下载(Binary download,而不是 trying source)而不用切换mac cpu架构 zhiwenwenzhiwenwendeMBP cockpit % nvm install 14.15.5 Downloading and installing node v14.15.5... Downloading https://node…...

【C++】开源:Muduo网络库配置与使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍Muduo网络库配置与使用。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下…...

VCS ICO - Intelligent Coverage Optimization
ico是vcs提供的用于优化覆盖率的feature;一般用户通过dist solver bofore等约束了变量的随机概率,而ico会在用户约束的基础上,做一些自动“修正”,以此来优化随机激励,提高随机多样性,加速覆盖率收敛&#…...
【分布式系统】分布式系统的8个谬误
网络可靠 对于分布式系统来说,网络、计算、存储是三大基石,系统之间进行拆分隔离之后,那么必定存在网络通讯,而网络是最不可靠的。 不管是从硬件层面还是软件层面来说,网络是不可靠的。(断电、配置错误、ID…...
tinkerCAD案例:25. 量角器 - 测量角度
tinkerCAD案例:25. 量角器 - 测量角度 原文 Now we’re going to make a protractor! A Protractor is one of the most basic, but essential, tools for making measurements. It is, then, surprising that the modern protractor is barely over 200 years ol…...

Flutter 使用texture_rgba_renderer实现桌面端渲染视频
Flutter视频渲染系列 第一章 Android使用Texture渲染视频 第二章 Windows使用Texture渲染视频 第三章 Linux使用Texture渲染视频 第四章 全平台FFICustomPainter渲染视频 第五章 Windows使用Native窗口渲染视频 第六章 桌面端使用texture_rgba_renderer渲染视频(本…...

linux虚拟机开机后桌面显示CentOS-7.5-x86盘片文件,并且无法远程连接虚拟机?
在虚拟机启动后遇到了显示CentOS-7.5-x86光盘片文件的问题,并且无法远程连接到虚拟机,有几个可能的解决方法: 检查虚拟机设置:确保虚拟机的网络适配器已正确配置,并且虚拟机配置的网络选项是桥接模式或 NAT 模式&#…...
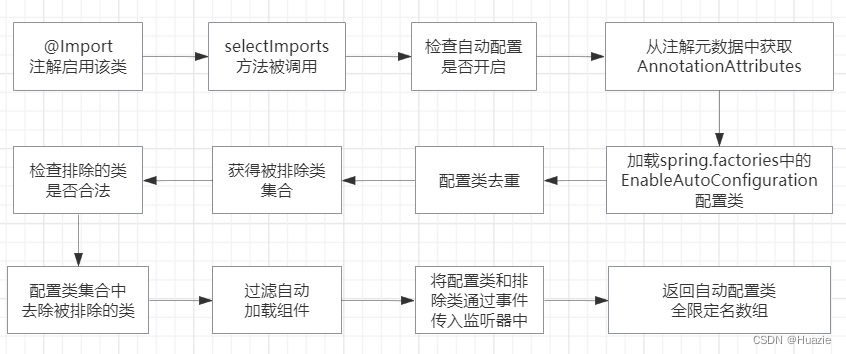
【Spring Boot 源码学习】走近 AutoConfigurationImportSelector
AutoConfigurationImportSelector 源码解析 引言主要内容1. ImportSelector 接口2. DeferredImportSelector 接口3. AutoConfigurationImportSelector 功能概述 总结 引言 上篇博文我们了解了 EnableAutoConfiguration 注解,其中真正实现自动配置功能的核心实现者 …...
)
系统学习Linux-MySQL数据库备份(四)
一、概述 数据库备份是指将数据库中的数据、表格、视图、存储过程、触发器等信息备份到另一个地方,一遍在数据库丢失或损坏时进行恢复,数据库备份是数据库管理中必不可少的一项工作,通过备份可以保护数据库中的数据和业务。 二、数据备份的…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

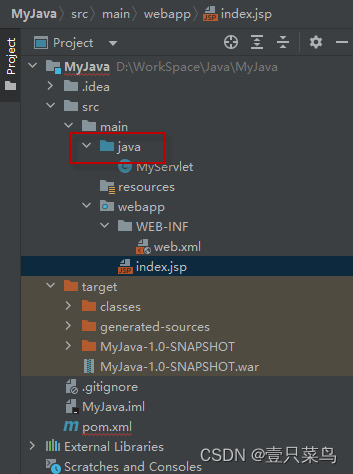
基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
