机器学习深度学习——权重衰减
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——模型选择、欠拟合和过拟合
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
权重衰减
- 讨论(思维过一下,后面会总结)
- 权重衰减
- 使用均方范数作为硬性限制
- 使用均方范数作为柔性限制
- 对最优解的影响
- 参数更新法则
- 总结
- 高维线性回归
- 从零开始实现
- 初始化模型参数
- 定义L2范数乘法
- 定义训练代码实现
- 忽略正则化直接训练
- 使用权重衰减
- 简洁实现
讨论(思维过一下,后面会总结)
前一节已经描述了过拟合的问题,本节将会介绍一些正则化模型的技术。
之前用了多项式回归的例子,我们可以通过调整拟合多项式的阶数来限制模型容量。而限制特征数量是缓解过拟合的一种常用技术。然而,我们还需要考虑高维输入可能发生的情况。多项式对多变量的自然扩展称为单项式,也可以说是变量幂的成绩。单项式的阶数是幂的和。例如,x12x2和x3x52都是3次单项式。
随着阶数d的增长,带有阶数d的项数迅速增加。给定k个变量,阶数为d的项的个数为:
C k − 1 + d k − 1 = ( k − 1 + d ) ! ( d ) ! ( k − 1 ) ! C_{k-1+d}^{k-1}=\frac{(k-1+d)!}{(d)!(k-1)!} Ck−1+dk−1=(d)!(k−1)!(k−1+d)!
因此即使是阶数上的微小变化,也会显著增加我们模型的复杂性。仅仅通过简单的限制特征数量,可能仍然使模型在过简单和过复杂中徘徊。我们需要一个更细粒度的工具来调整函数的复杂性,使其达到一个合适的平衡位置。
在之前已经描述了L2范数和L1范数。
在训练参数化机器学习模型时,权重衰减是最广泛使用的正则化的技术之一,它通常被称为L2正则化。这项技术通过函数与0的距离来衡量函数的复杂度,因为所有的函数f中,f=0在某种意义上是最简单的。但是衡量函数f与0的距离并不简单,这也没有一个正确的答案。
一种简单的方法是通过线性函数f(x)=wTx中的某个向量的范数来度量其复杂性,例如||w||2。要保证权重向量比较小,最常用方法是将其范数作为惩罚项加到最小化损失的问题中。将原来的训练目标最小化训练标签上的预测损失,调整为最小化预测损失和惩罚项之和。如果我们的权重向量增长的太大,我们的学习算法可能更集中于最小化权重范数||w||2。回归线性回归,我们的损失由下式给出:
L ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w T x ( i ) + b − y ( i ) ) 2 L(w,b)=\frac{1}{n}\sum_{i=1}^n\frac{1}{2}(w^Tx^{(i)}+b-y^{(i)})^2 L(w,b)=n1i=1∑n21(wTx(i)+b−y(i))2
其中,x(i)是样本i的特征,y(i)是样本i的标签,(w,b)是权重和偏置参数。
为了乘法权重向量的大小,我们现在在损失函数添加||w||2,模型如何平衡这个新的额外乘法的损失?我们通过正则化常数λ来描述这种权衡(这是一个非负超参数,我们使用验证数据拟合):
L ( w , b ) + λ 2 ∣ ∣ w ∣ ∣ 2 L(w,b)+\frac{\lambda}{2}||w||^2 L(w,b)+2λ∣∣w∣∣2
对于λ=0,我们恢复了原来的损失函数。对于λ>0,我们限制||w||的大小。这里我们仍然除以2(当我们取一个二次函数的导数时, 2和1/2会抵消)。
对于范数的选择,可以提出两个问题:
1、为什么不选择欧几里得距离?
2、为什么不用L1范数?
对于第1个问题:这样做就是为了通过平方去掉L2范数的平方根,留下权重向量每个分量的平方和,这样就很好进行求导了(此时导数的和就等于和的导数)
对于第2个问题:L2范数比起L1范数,对权重向量的大分量施加了巨大的惩罚,在这里还是L2更适合。
那么L2正则化回归的小批量随机梯度下降更新如下式:
w ← ( 1 − η λ ) w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( w T x ( i ) + b − y ( i ) ) w←(1-ηλ)w-\frac{η}{|B|}\sum_{i∈B}x^{(i)}(w^Tx^{(i)}+b-y^{(i)}) w←(1−ηλ)w−∣B∣ηi∈B∑x(i)(wTx(i)+b−y(i))
为啥是这个结果可以看后面的推导,这个结论说明:我们根据估计值和观测值之间的差距来更新w,同时也在试图缩小w的大小,这就叫权重衰减(或权重衰退)。
权重衰减为我们提供了一种连续的机制来调整函数复杂度,较小的λ值对应较少约束的w,较大的λ值对w的约束会更大。
权重衰减
使用均方范数作为硬性限制
1、通过限制参数值的选择范围来控制模型容量:
m i n l ( w , b ) 其中 ∣ ∣ w ∣ ∣ 2 ≤ θ min l(w,b)其中||w||^2≤θ minl(w,b)其中∣∣w∣∣2≤θ
2、通常不限制偏移b(其实限制不限制都差不多)
3、更小的θ意味着更强的正则项
使用均方范数作为柔性限制
1、对每个θ,都可以找到λ使得之前的目标函数等价于
m i n l ( w , b ) + λ 2 ∣ ∣ w ∣ ∣ 2 min l(w,b)+\frac{\lambda}{2}||w||^2 minl(w,b)+2λ∣∣w∣∣2
2、上式通过拉格朗日乘子就能证明
3、超参数λ控制了正则项的重要程度
λ = 0 :无作用 λ → ∞ : w ∗ → 0 \lambda=0:无作用\\ \lambda→∞:w^*→0 λ=0:无作用λ→∞:w∗→0
对最优解的影响
一张图片就能看出来:
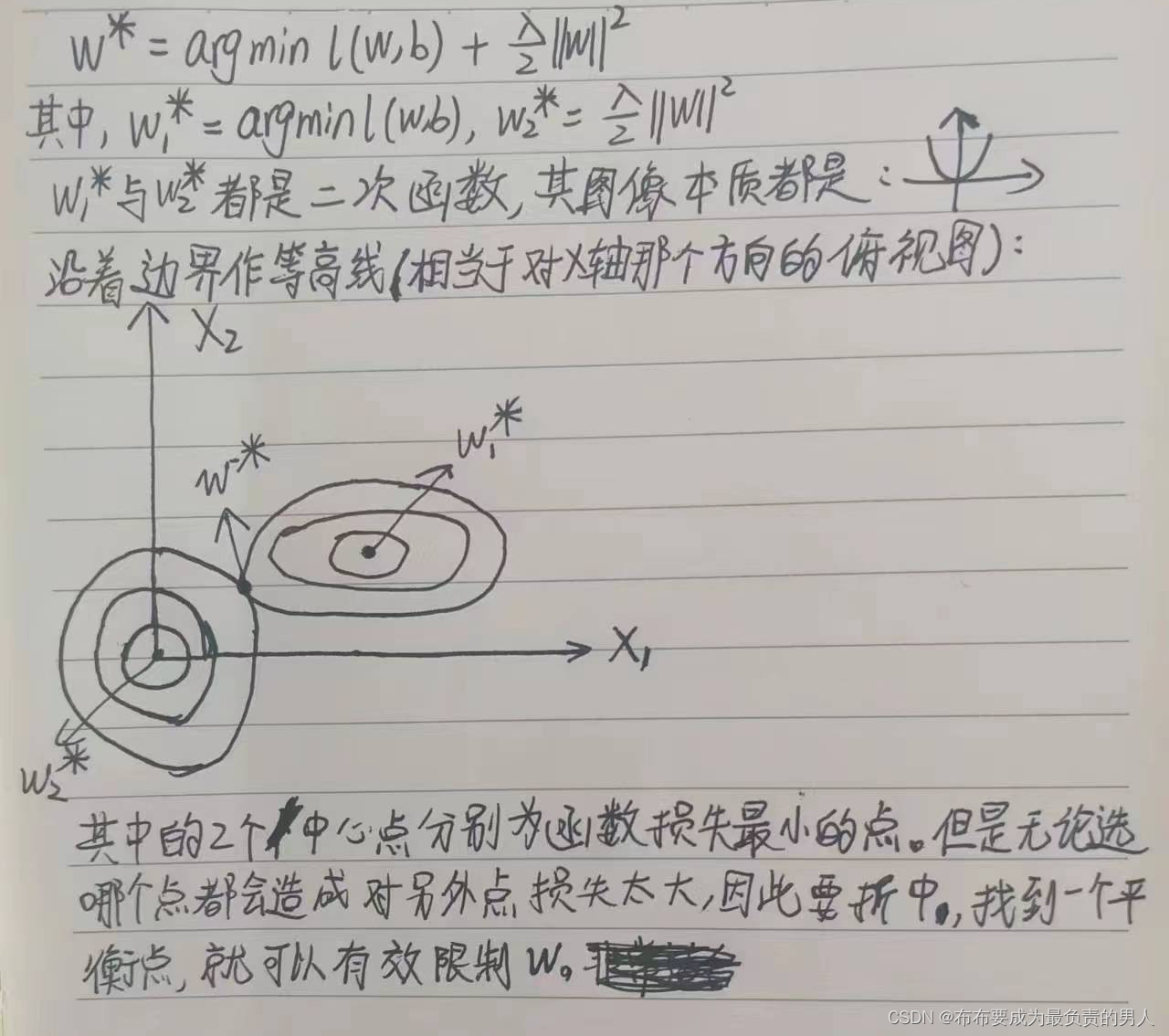
参数更新法则
计算梯度:
∂ ∂ w ( l ( w , b ) + λ 2 ∣ ∣ w ∣ ∣ 2 ) = ∂ l ( w , b ) ∂ w + λ w \frac{\partial}{\partial w}(l(w,b)+\frac{\lambda}{2}||w||^2)=\frac{\partial l(w,b)}{\partial w}+\lambda w ∂w∂(l(w,b)+2λ∣∣w∣∣2)=∂w∂l(w,b)+λw
时间t更新参数:
w t + 1 = w t − η ∂ ∂ w 把 ∂ ∂ w 用上式带入,得: w t + 1 = ( 1 − η λ ) w t − η ∂ l ( w t , b t ) ∂ w t w_{t+1}=w_t-η\frac{\partial}{\partial w}\\把\frac{\partial}{\partial w}用上式带入,得:\\w_{t+1}=(1-η\lambda)w_t-η\frac{\partial l(w_t,b_t)}{\partial w_t} wt+1=wt−η∂w∂把∂w∂用上式带入,得:wt+1=(1−ηλ)wt−η∂wt∂l(wt,bt)
通常ηλ<1,在深度学习中叫作权重衰退。
(可以和之前的梯度做比较,会发现也就是在w之前加了个(1-ηλ)的系数,这样就可以做到权重衰退)
总结
1、权重衰退通过L2正则项使得模型参数不会太大,从而控制模型复杂度。
2、正则项权重是控制模型复杂度的超参数。
高维线性回归
我们通过简单例子来演示权重衰减
import torch
from torch import nn
from d2l import torch as d2l
生成一些人工数据集,生成公式如下:
y = 0.05 + ∑ i = 1 d 0.01 x i + σ 其中 σ 符合正态分布 N ( 0 , 0.0 1 2 ) y=0.05+\sum_{i=1}^d0.01x_i+\sigma\\ 其中\sigma符合正态分布N(0,0.01^2) y=0.05+i=1∑d0.01xi+σ其中σ符合正态分布N(0,0.012)
为了把过拟合体现的更明显,我们的训练集就只有20个(数据越简单越容易过拟合)
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
从零开始实现
下面从头开始实现权重衰减,只需将L2的平方惩罚添加到原始目标函数值。
初始化模型参数
def init_params():w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)b = torch.zeros(1, requires_grad=True)return [w, b]
定义L2范数乘法
我们这边是在原来的L2基础上加上了平方,从而去除了他的根号。
def l2_penalty(w):return torch.sum(w.pow(2)) / 2
定义训练代码实现
下面将模型与训练数据集进行拟合,并在测试数据集上进行评估。其中线性网络与平方损失是没有变化的,唯一的变化只是现在增加了惩罚项。
def train(lambd):w, b = init_params()# lambda X相当于定义了一个net()函数,不好理解少用net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_lossnum_epochs, lr = 100, 0.003animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])for epoch in range(num_epochs):for X, y in train_iter:# 增加L2范数惩罚项# 广播机制使L2_penalty(w)成为一个长度为batch_size的向量l = loss(net(X), y) + lambd * l2_penalty(w)l.sum().backward()d2l.sgd([w, b], lr, batch_size)if (epoch + 1) % 5 == 0:animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数是:', torch.norm(w).item())
忽略正则化直接训练
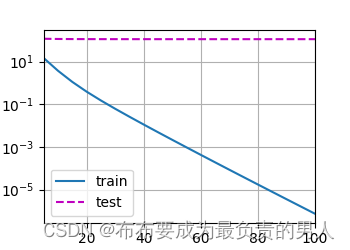
此时,我们使用lambd=0来禁止权重衰减,运行代码以后,训练误差会减少,但是测试误差却没有减少,说明出现了严重的过拟合。
train(lambd=0)
d2l.plt.show()
运行结果:
w的L2范数是: 13.375638008117676
运行图片:
使用权重衰减
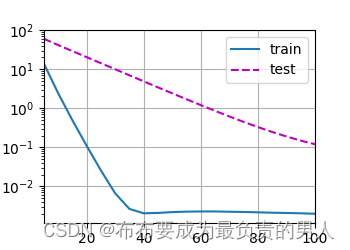
这里的训练误差增大,但测试误差减小,这正是期望从正则化中得到的效果。
train(lambd=3)
d2l.plt.show()
运行结果:
w的L2范数是: 0.35898885130882263
运行图片:
简洁实现
由于权重衰减在神经网络优化中很常用,深度学习框架就将权重衰减集成到优化算法中,以便与任何损失函数结合使用。此外,这种集成还有计算上的好处,允许在不增加任何额外的计算开销的情况下向算法中添加权重衰减。由于更新的权重衰减部分仅依赖于每个参数的当前值,因此优化器必须至少接触每个参数一次。
在下面的代码中,我们在实例化优化器时直接通过weight_decay指定weight decay超参数。 默认情况下,PyTorch同时衰减权重和偏移。 这里我们只为权重设置了weight_decay,所以偏置参数b不会衰减。
import torch
from torch import nn
from d2l import torch as d2ln_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)def train_concise(wd):net = nn.Sequential(nn.Linear(num_inputs, 1))for param in net.parameters():param.data.normal_()loss = nn.MSELoss(reduction='none')num_epochs, lr = 100, 0.003# 偏置参数没有衰减trainer = torch.optim.SGD([{"params": net[0].weight, 'weight_decay': wd},{"params": net[0].bias}], lr=lr)animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])for epoch in range(num_epochs):for X, y in train_iter:trainer.zero_grad()l = loss(net(X), y)l.mean().backward()trainer.step()if (epoch + 1) % 5 == 0:animator.add(epoch + 1,(d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数:', net[0].weight.norm().item())
测试运行:
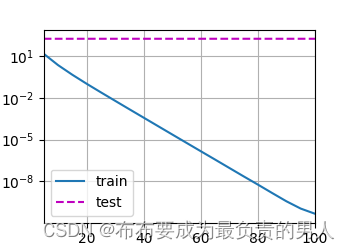
train_concise(0)
d2l.plt.show()
运行结果:
w的L2范数: 14.566418647766113
运行图片:
测试运行:
train_concise(3)
d2l.plt.show()
运行结果:
w的L2范数: 0.45850494503974915
运行图片:

运行后的图和之前的图相同,但是它们运行得更快,更容易实现。对于复杂问题,这一好处将变得更加明显。
后序的内容,在深层网络的所有层上,都会应用权重衰减。
相关文章:

机器学习深度学习——权重衰减
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——模型选择、欠拟合和过拟合 📚订阅专栏:机器学习&&深度学习 希望文章对你…...
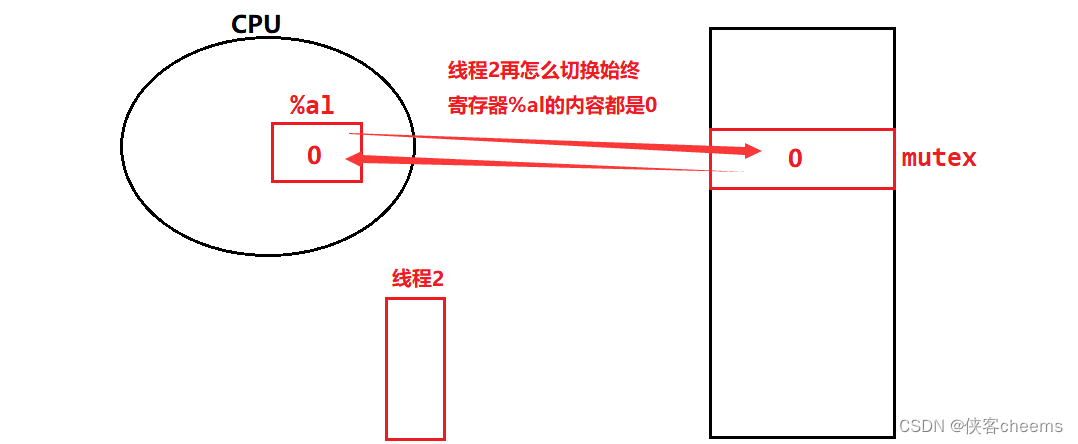
【Linux】线程互斥 -- 互斥锁 | 死锁 | 线程安全
引入互斥初识锁互斥量mutex锁原理解析 可重入VS线程安全STL中的容器是否是线程安全的? 死锁 引入 我们写一个多线程同时访问一个全局变量的情况(抢票系统),看看会出什么bug: // 共享资源, 火车票 int tickets 10000; //新线程执行方法 vo…...

【vue-pdf】PDF文件预览插件
1 插件安装 npm install vue-pdf vue-pdf GitHub:https://github.com/FranckFreiburger/vue-pdf#readme 参考文档:https://www.cnblogs.com/steamed-twisted-roll/p/9648255.html catch报错:vue-pdf组件报错vue-pdf Cannot read properti…...

Flink集群运行模式--Standalone运行模式
Flink集群运行模式--Standalone运行模式 一、实验目的二、实验内容三、实验原理四、实验环境五、实验步骤5.1 部署模式5.1.1 会话模式(Session Mode)5.1.2 单作业模式(Per-Job Mode)5.1.3 应用模式(Application Mode&a…...

Spring整合JUnit实现单元测试
Spring整合JUnit实现单元测试 一、引言 在软件开发过程中,单元测试是保证代码质量和稳定性的重要手段。JUnit是一个流行的Java单元测试框架,而Spring是一个广泛应用于Java企业级开发的框架。本文将介绍如何使用Spring整合JUnit实现单元测试,…...

Spring Boot学习路线1
Spring Boot是什么? Spring Boot是基于Spring Framework构建应用程序的框架,Spring Framework是一个广泛使用的用于构建基于Java的企业应用程序的开源框架。Spring Boot旨在使创建独立的、生产级别的Spring应用程序变得容易,您可以"只是…...

管理类联考——写作——论说文——实战篇——标题篇
角度3——4种材料类型、4个立意对象、5种写作态度 经过审题立意后,我们要根据我们的立意,确定一个主题,这个主题必须通过文章的标题直接表达出来。 标题的基本要求 主题清晰,态度明确 第一,阅卷人看到一篇论说文的标…...
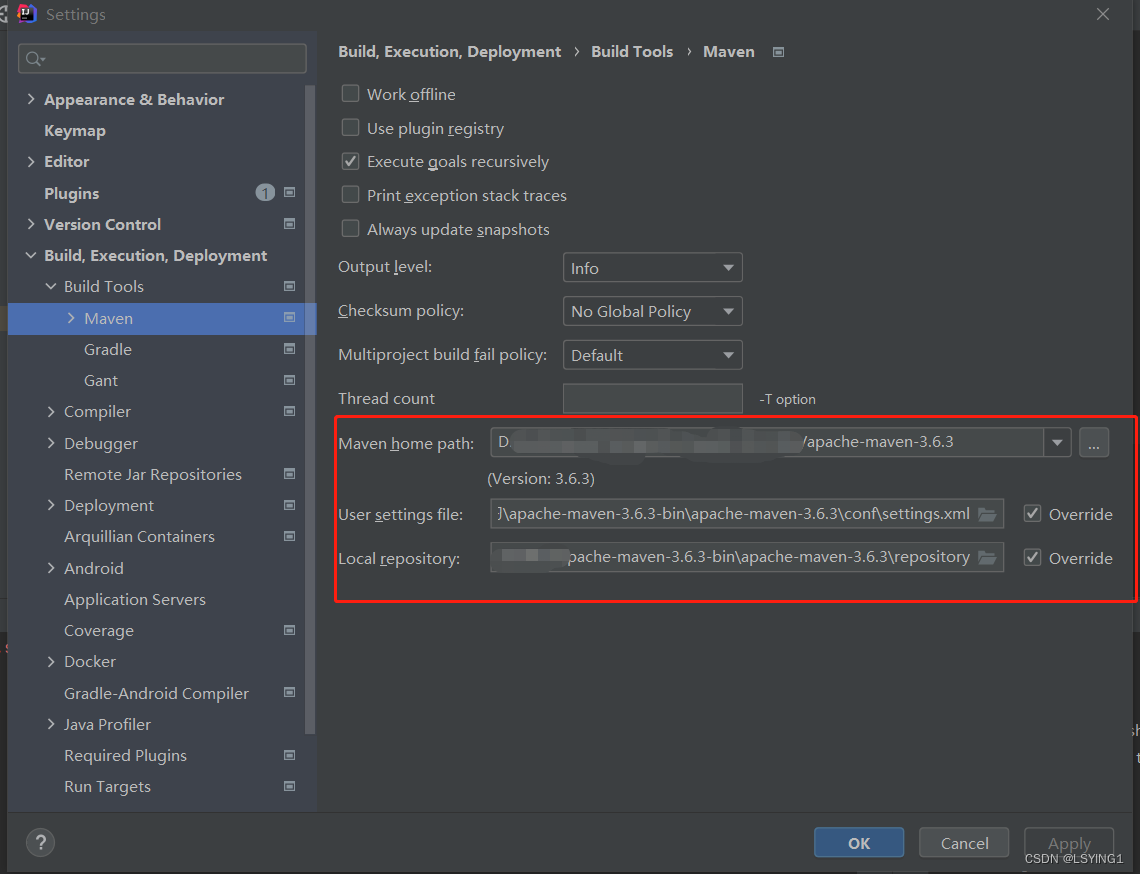
idea中设置maven本地仓库和自动下载依赖jar包
1.下载maven 地址:maven3.6.3 解压缩在D:\apache-maven-3.6.3-bin\apache-maven-3.6.3\目录下新建文件夹repository打开apache-maven-3.6.3-bin\apache-maven-3.6.3\conf文件中的settings.xml编辑:新增本地仓库路径 <localRepository>D:\apache-…...
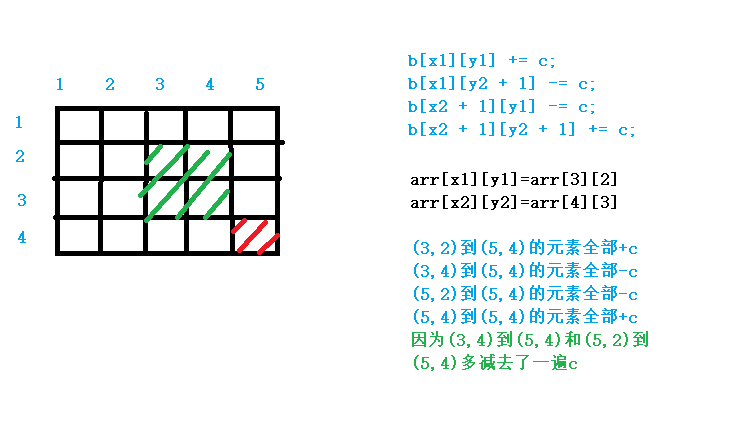
前缀和差分
前缀和 前缀和:一段序列里的前n项和 给出n个数,在给出q次问询,每次问询给出L、R,快速求出每组数组中一段L至R区间的和 给出一段数组,每次问询为求出l到r区间的和 普通方法:L到R进行遍历,那么…...
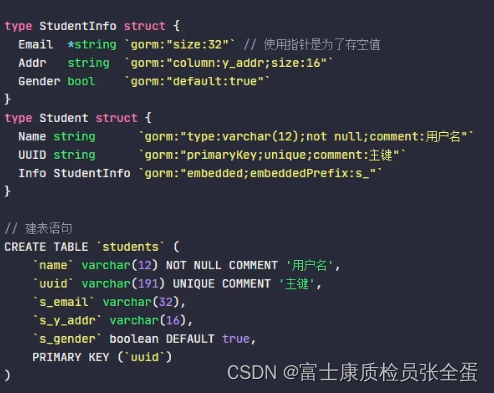
Golang GORM 模型定义
模型定义 参考文档:https://gorm.io/zh_CN/docs/models.html 模型一般都是普通的 Golang 的结构体,Go的基本数据类型,或者指针。 模型是标准的struct,由Go的基本数据类型、实现了Scanner和Valuer接口的自定义类型及其指针或别名组成&#x…...
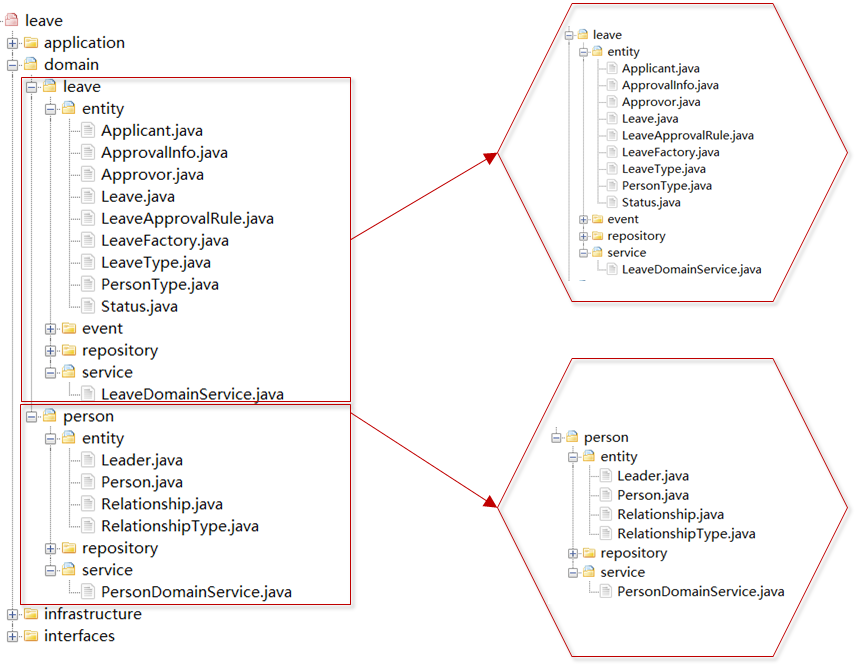
微服务的各种边界在架构演进中的作用
演进式架构 在微服务设计和实施的过程中,很多人认为:“将单体拆分成多少个微服务,是微服务的设计重点。”可事实真的是这样吗?其实并非如此! Martin Fowler 在提出微服务时,他提到了微服务的一个重要特征—…...

使用 docker-compose 一键部署多个 redis 实例
目录 1. 前期准备 2. 导入镜像 3. 部署redis master脚本 4. 部署redis slave脚本 5. 模板文件 6. 部署redis 7. 基本维护 1. 前期准备 新部署前可以从仓库(repository)下载 redis 镜像,或者从已有部署中的镜像生成文件: …...
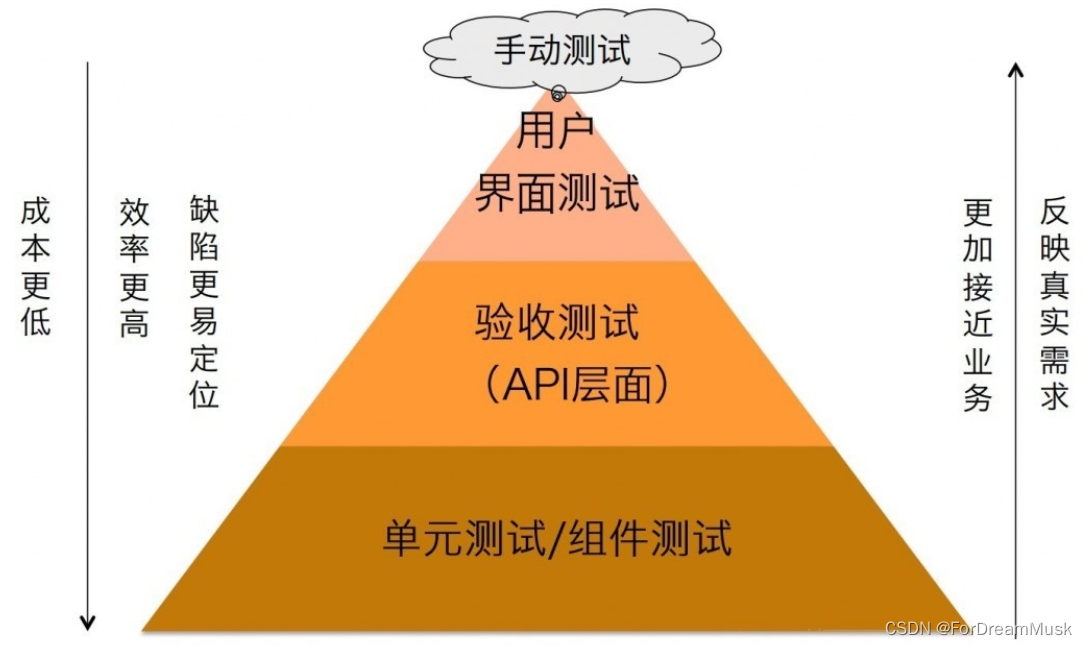
14-测试分类
1.按照测试对象划分 ①界面测试 软件只是一种工具,软件与人的信息交流是通过界面来进行的,界面是软件与用户交流的最直接的一层,界面的设计决定了用户对设计的软件的第一印象。界面如同人的面孔,具有吸引用户的直接优势…...

打开域名跳转其他网站,官网被黑解决方案(Linux)
某天打开网站,发现进入首页,马上挑战到其他赌博网站。 事不宜迟,不能让客户发现,得马上解决 我的网站跳转到这个域名了 例如网站跳转到 k77.cc 就在你们部署的代码的当前文件夹下面,执行下如下命令 find -type …...

redis总结
1.redis redis高性能的key-value数据库,支持持久化,不仅仅支持简单的key-value,还提供了list,set,zset,hash等数据结构的存储,支持数据的备份(master-slave模式) redis&…...
现代C++中的从头开始深度学习:激活函数
一、说明 让我们通过在C中实现激活函数来获得乐趣。人工神经网络是生物启发模型的一个例子。在人工神经网络中,称为神经元的处理单元被分组在计算层中,通常用于执行模式识别任务。 在这个模型中,我们通常更喜欢控制每一层的输出以服从一些约束…...

python怎么实现tcp和udp连接
目录 什么是tcp连接 什么是udp连接 python怎么实现tcp和udp连接 什么是tcp连接 TCP(Transmission Control Protocol)连接是一种网络连接,它提供了可靠的、面向连接的数据传输服务。 在TCP连接中,通信的两端(客户端和…...
)
java设计模式-观察者模式(jdk内置)
上一篇我们学习了 观察者模式。 观察者和被观察者接口都是我们自己定义的,整个设计模式我们从无到有都是自己设计的,其实,java已经内置了这个设计模式,我们只需要定义实现类即可。 下面我们不多说明,直接示例代码&am…...

秒级体验本地调试远程 k8s 中的服务
点击上方蓝色字体,选择“设为星标” 回复”云原生“获取基础架构实践 背景 在这个以k8s为云os的时代,程序员在日常的开发过程中,肯定会遇到各种问题,比如:本地开发完,需要部署到远程k8s集群,本地…...

CV前沿方向:Visual Prompting 视觉提示工程下的范式
prompt在视觉领域,也越来越重要,在图像生成,作为一种可控条件,增进交互和可控性,在多模态理解方面,指令prompt也使得任务灵活通用。视觉提示工程,已然成为CV一个前沿方向! 下面来看看…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
