Leetcode力扣秋招刷题路-0073
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结
73. 矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
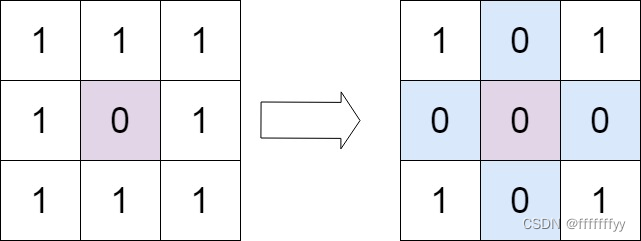
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
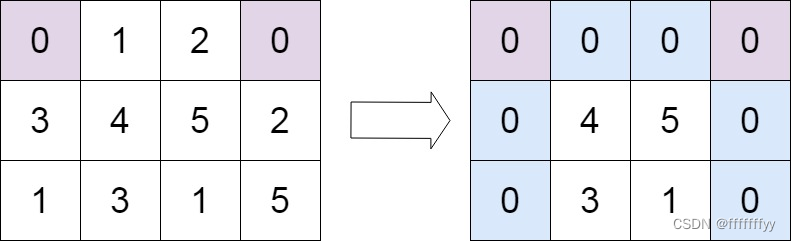
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
−231-2^31−231 <= matrix[i][j] <= 231−12^31 - 1231−1
进阶:
一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗?
方法一
思路:用两个set分别记录需要置0的行和需要置0的列。第一次遍历矩阵时,若发现一个元素为0,则将其行和列值分别加入到两个set中。第二次遍历矩阵时,将行set中的行全部置0,将列set中的列全部置0。
public void setZeroes(int[][] matrix) {if(matrix == null || matrix.length == 0)return;int m = matrix.length, n = matrix[0].length;Set<Integer> row = new HashSet<Integer>();Set<Integer> col = new HashSet<Integer>();for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(matrix[i][j] == 0){row.add(i);col.add(j);}}}for(int i : row){for(int j = 0; j < n; j++)matrix[i][j] = 0;}for(int j : col){for(int i = 0; i < m; i++)matrix[i][j] = 0;}
}
时间复杂度:O(m×n)
空间复杂度:O(m+n) 最坏情况是矩阵中全部元素为0的情况,这时两个set的大小分别为m和n。
方法二
思路:不用额外空间,让首行和首列记录某列和某行是否有0
算法步骤:
首先用两个布尔类型变量firstRow和firstCol分别记录矩阵的首行和首列中是否有0
遍历除首行和首列外的所有元素,若元素matrix[i][j]为0,则将它对应的首行和首列中的元素matrix[i][0]和matrix[0][j]置为0,意为此行和列后续需要被置0(由于修改后首行和首列是否有0的信息会被破坏掉,因此需要有之前的步骤一)
遍历首行和首列,若发现首行中有元素为0,则将此元素所处的列全部置0,若发现首列中有元素为0,则将此元素所处的行全部置0。
根据步骤一的布尔类型变量firstRow和firstCol来判断首行和首列是否需要被置0。
public void setZeroes(int[][] matrix) {if(matrix == null || matrix.length == 0)return;int m = matrix.length, n = matrix[0].length;boolean firstRow = false, firstCol = false;//步骤一for(int i = 0; i < m; i++){if(matrix[i][0] == 0)firstCol = true;}for(int j = 0; j < n; j++){if(matrix[0][j] == 0)firstRow = true;}//步骤二for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){if(matrix[i][j] == 0){matrix[i][0] = 0;matrix[0][j] = 0;}}}//步骤三for(int i = 1; i < m; i++){if(matrix[i][0] == 0){for(int j = 0; j < n; j++)matrix[i][j] = 0;}}for(int j = 1; j < n; j++){if(matrix[0][j] == 0){for(int i = 0; i < m; i++)matrix[i][j] = 0;}}//步骤四if(firstRow){for(int j = 0; j < n; j++)matrix[0][j] = 0;}if(firstCol){for(int i = 0; i < m; i++)matrix[i][0] = 0;}
}
时间复杂度:O(m×n)
空间复杂度:O(1)
相关文章:

Leetcode力扣秋招刷题路-0073
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结 73. 矩阵置零 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 输入:mat…...

遥感数字图像处理
遥感数字图像处理 来源:慕课北京师范大学朱文泉老师的课程 遥感应用:遥感制图、信息提取 短期内了解知识结构–>有选择的剖析经典算法原理–>系统化知识结构、并尝试实践应用 跳出算法(尤其是数学公式) 关注原理及解决问…...
深度学习常用的python函数(一)
由于我只简单的学过python和pytorch,其中有很多函数的操作都还是一知半解的,其中有些函数经常见到,所以就打算记录下来。 1.zip zip(*a):针对单个可迭代对象压缩成n个元组,元组数量n等于min(a中元素的最小长度) a [(1, 2), (3…...
2023年美国大学生数学建模A题:受干旱影响的植物群落建模详解+模型代码(一)
目录 前言 一、题目理解 背景 解析: 要求 二、建模 1.相关性分析 2.相关特征权重 只希望各位以后遇到建模比赛可以艾特认识一下我,我可以提供免费的思路和部分源码,以后的数模比赛只要我还有时间肯定会第一时间写出免费开源思路&…...
PPS文件如何转换成PPT?附两种方法
在工作中,PPS文件的使用还是很广泛的,因为作为幻灯片放映文件,点击后就能直接播放,十分方便。但如果想要修改PPS里的内容,PPS是无法编辑的,我们需要把文件转换成PPT,再进行修改。 那PPS文件如何…...
ParallelsDesktop安装【亲测可行】
我这边安装的是macos最新系统 (Ventura13.2) 本文参考这篇文章安装,但是你完全按照这篇文章会报错,具体可行操作记录如下 一、下载软件和补丁 1、点这里去下载补丁18.0.1 2、点这里去下载对应版本的ParallelsDesktop18.0.1,安装上到试用这里…...
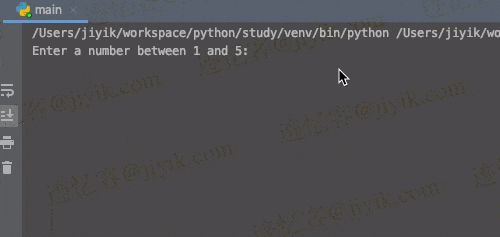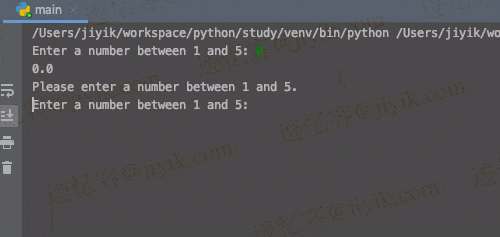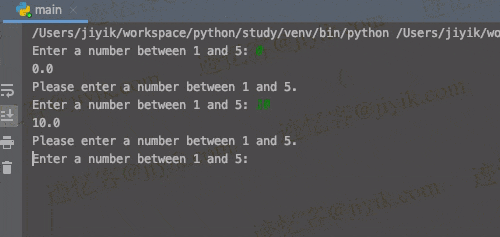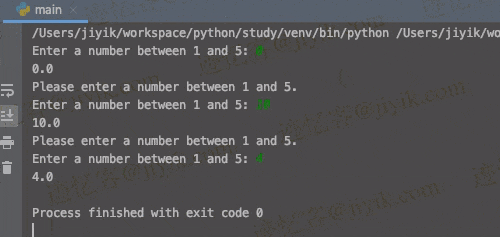
在 Python 中只接受数字作为用户输入
只接受数字作为用户输入: 使用 while True 循环进行循环,直到用户输入一个数字。使用 float() 类尝试将值转换为浮点数。如果用户输入了一个数字,请使用 break 语句跳出循环。 while True:try:# 👇️ use int() instead of floa…...
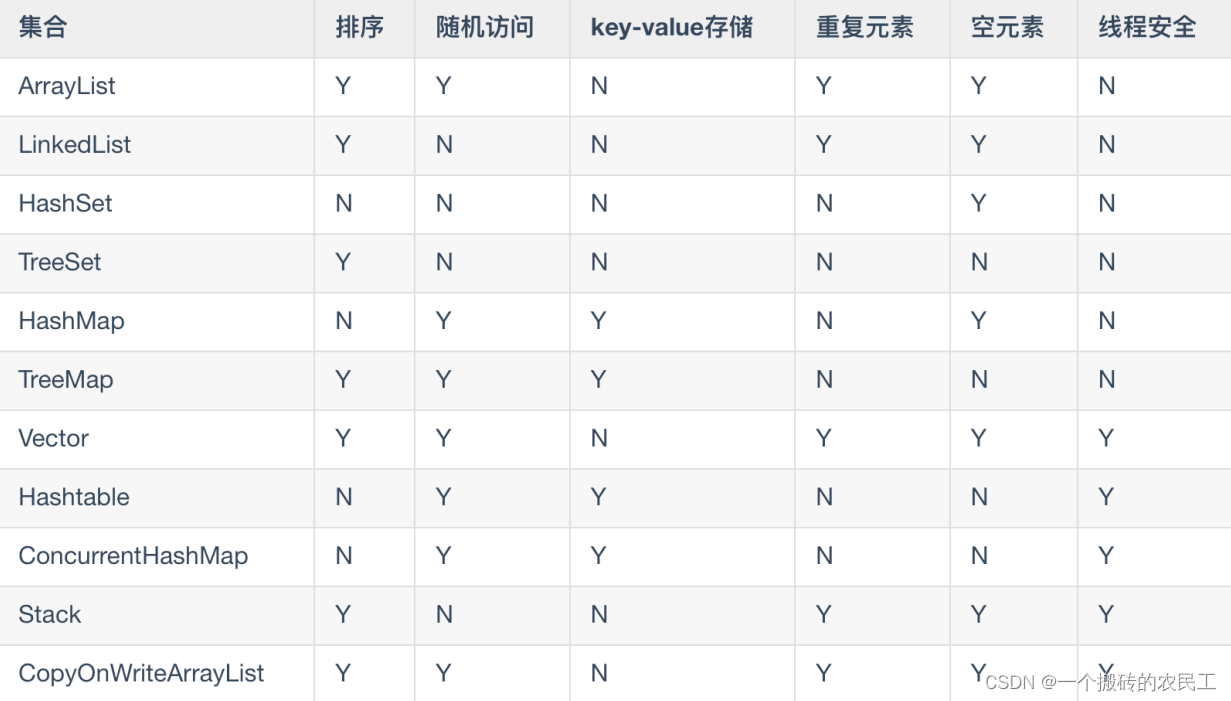
【集合】JAVA基础篇(二)
目录一、java常用集合1、Java集合接口的作用2、Java集合常用实现类的作用二、Collection 常用的方法三、List 集合接口1、ArrayList类的常用方法2、LinkList类中的方法3、Vector4、ArrayList 类和 LinkedList 类的区别四、Set 集合1、HashSet 类2、TreeSet 类3、HashSet 和 Tre…...

机房意外掉电导致Elasticsearch的部分index无数据的修复过程
环境 :华为大数据集群FusionInsight V100R002C800SPC200、Elasticsearch 6.1.3、Kibana问题产生原因:因机房意外掉电导致集群部分机器两次掉电导致Elasticsearch重启,Elasticsearch重启后看似正常但某些index无数据。经排查判断为Elasticsearch的部分ind…...
Spring入门案例三:注解进行引用类型的自动装配
本系列文章将会带领大家进行Spring的全面学习,持续关注我,不断更新中… 一.案例分级 简单解析:配置类替代以前的配置文件,实体类提供对象,业务类中有实体类的引用对象,在业务层中实现引用类的自动装配。 二.各层代码…...

kubernet + kubevirt + ceph 汇总文档
目的 1 创建 kubenetes 集群 2 kubenetes 集群上部署 kubevirt 3 kubernetes 支持 ceph 存储 4 VMI 可以存储在 ceph rbd 存储中并正常使用 参考部署文档 名称连接备注centos8 + kubernetes 1.24 master/node 节点部署文档kubernetes 集群部署kubectl top node 使用方法部署文档…...

软件测试项目实战(附全套实战项目教程+视频+源码)
开通博客以来,我更新了很多实战项目,但一部分小伙伴在搭建环境时遇到了问题。 于是,我收集了一波高频问题,汇成本篇,供大家参考,避免重复踩坑。 如果你还遇到过其他坑和未解决的问题,可在评论区…...

Python seek()和tell()函数详解
在讲解 seek() 函数和 tell() 函数之前,首先来了解一下什么是文件指针。我们知道,使用 open() 函数打开文件并读取文件中的内容时,总是会从文件的第一个字符(字节)开始读起。那么,有没有办法可以自定指定读…...
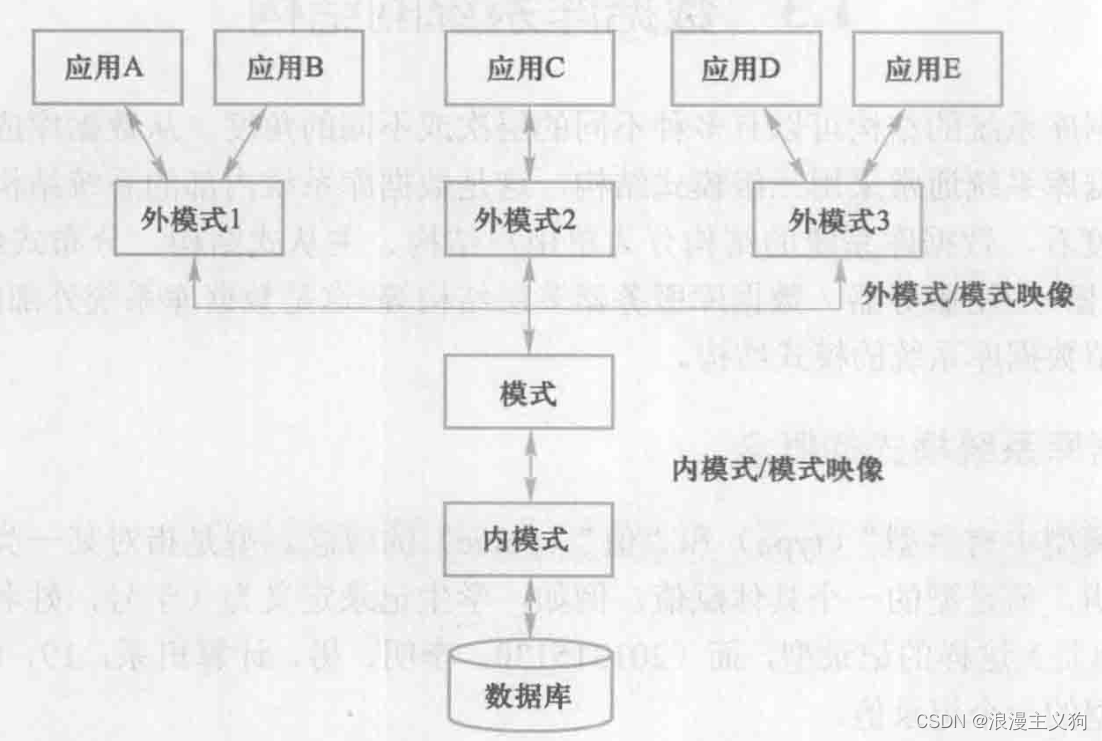
数据库系统:1. 绪论
更好的阅读体验\huge{\color{red}{更好的阅读体验}}更好的阅读体验 文章目录1.1 数据库系统概述1.1.1 基本概念数据(data)数据库(DataBase, DB)数据库管理系统(DataBase Management System, DBMS)数据库系统…...

Android App开发基础
文章目录一 App的开发特点1.1 App的运行环境1.2 App开发语言1.3 java语言开发1.4 Kotlin语言开发1.5 XML1.6 App连接的数据库二 App的工程结构2.1 App工程目录结构2.2 构建工具Grade2.3 编译配置文件build.gradle2.4 运行配置文件AndroidManifest.xml2.4.1 application2.4.2 ac…...

力扣-分数排名
大家好,我是空空star,本篇带你了解一道简单的力扣sql练习题。 文章目录前言一、题目:178. 分数排名二、解题1.错误示范①提交SQL运行结果2.错误示范②提交SQL运行结果3.正确示范①提交SQL运行结果4.正确示范②提交SQL运行结果5.正确示范③提交…...
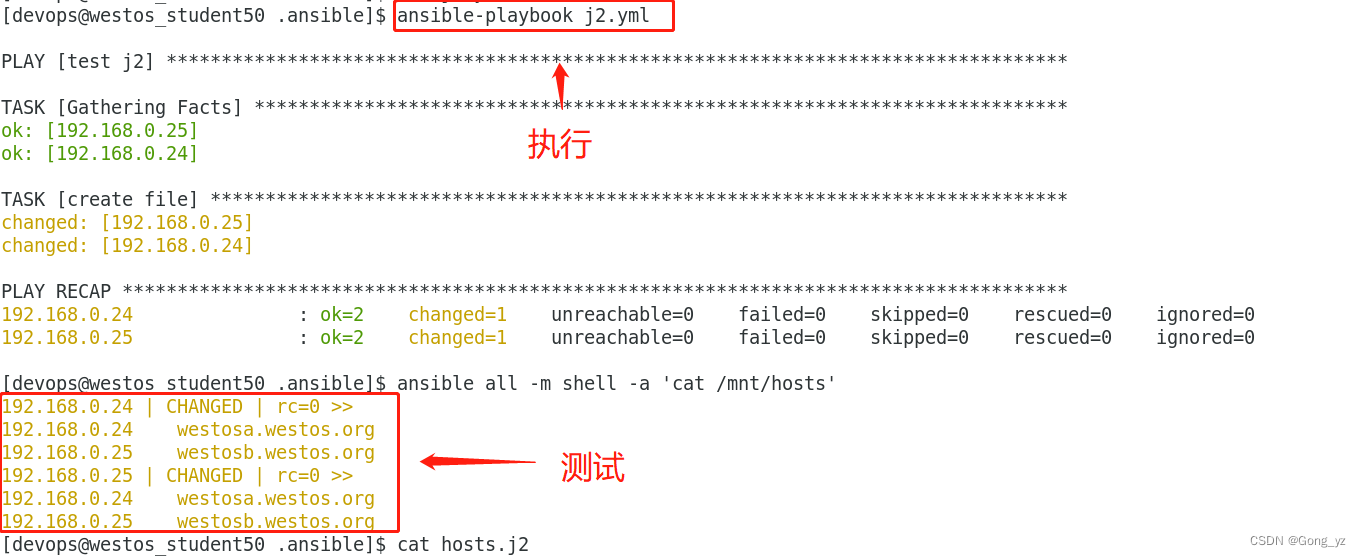
图文详解Ansible中的变量及加密
文章目录一、变量命名二、变量级别三、.变量设定和使用方式1.在playbook中直接定义变量2.在文件中定义变量3.使用变量4.设定主机变量和清单变量5.目录设定变量6.用命令覆盖变量7.使用数组设定变量8.注册变量9.事实变量10.魔法变量四、JINJA2模板五、 Ansible的加密控制练习1.用…...
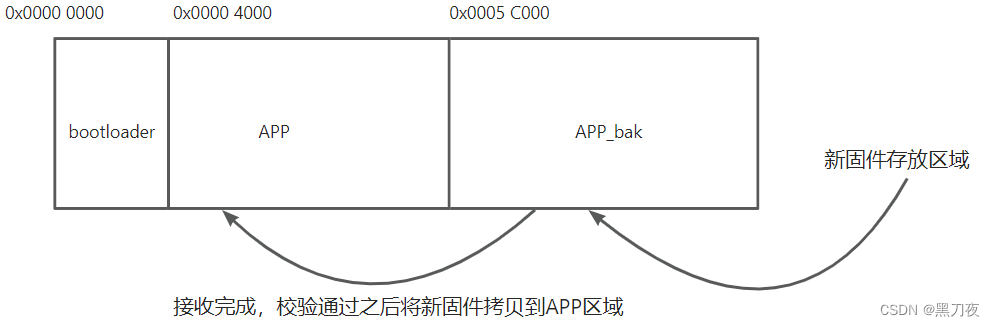
silicon labs平台通过串口升级固件方案
开发环境 windowssimplicity studio 5geck sdk 4.1 一 bootloader 新建BGAPI UART DFU工程 工程新建完成以后看一下linkerfile.ld文件的flash和ram的配置跟自己的application工程是否对应得上 配置串口波特率和引脚 默认使用PB0进入bootloader模式,这里改成Non…...
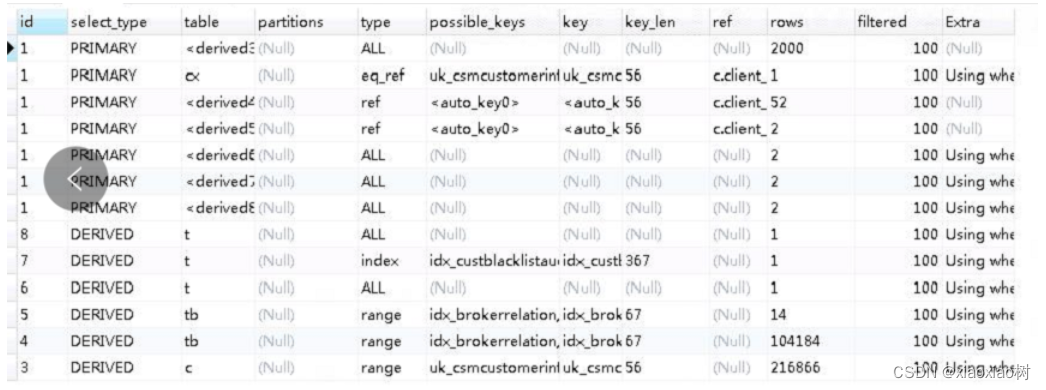
MySQL 派生表产生关联索引auto_key0导致SQL非常的慢
相同的SQL在maridb运行0.5秒,在MySQL8.0.26中运行要19秒 官方MySQL在处理子查时,优化器有个优化参数derived_merge,MySQL7开启添加,默认on.很多情况可以自动优化派生表,避免创建临时索引auto_key0和生成临时表数据做…...

计算机网络期末复习汇总(附某高校期末真题试卷)
文章目录一、选择题二、填空题三、名词解析四、简答题五、高校期末真题一、选择题 1、传输延迟时间最小的交换方法是( A ) A.电路交换 B.报文交换 C.分组交换 D.信元交换 2、在OSI七层结构模型中,处于数据链路层与运输层之间的是( B) A、物…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
