打卡力扣题目十二
#左耳听风 ARST 打卡活动重启#
目录
一、问题
二、解题方法一
三、解题方法二
关于 ARTS 的释义 —— 每周完成一个 ARTS:
● Algorithm: 每周至少做一个 LeetCode 的算法题
● Review: 阅读并点评至少一篇英文技术文章
● Tips: 学习至少一个技术技巧
● Share: 分享一篇有观点和思考的技术文章
希望通过此次活动能聚集一波热爱技术的人,延续好奇、探索、实践、分享的精神。
一、问题
给定一个非空且只包含非负数的整数数组 nums,数组的 度 的定义是指数组里任一元素出现频数的最大值。
你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。
示例 1:
输入:nums = [1,2,2,3,1]
输出:2
解释:
输入数组的度是 2 ,因为元素 1 和 2 的出现频数最大,均为 2 。
连续子数组里面拥有相同度的有如下所示:
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
最短连续子数组 [2, 2] 的长度为 2 ,所以返回 2 。
示例 2:
输入:nums = [1,2,2,3,1,4,2]
输出:6
解释:
数组的度是 3 ,因为元素 2 重复出现 3 次。
所以 [2,2,3,1,4,2] 是最短子数组,因此返回 6 。
提示:
nums.length 在 1 到 50,000 范围内。
nums[i] 是一个在 0 到 49,999 范围内的整数。
二、解题方法一
def findShortestSubArray(nums):# 统计每个数字出现的频数和第一次出现的位置count = {}first_occurrence = {}max_degree = 0for i, num in enumerate(nums):if num not in count:count[num] = 1first_occurrence[num] = ielse:count[num] += 1# 更新最大度if count[num] > max_degree:max_degree = count[num]# 找到与最大度相同的数字的最短连续子数组长度min_length = float('inf')for num in count:if count[num] == max_degree:length = i - first_occurrence[num] + 1if length < min_length:min_length = lengthreturn min_length这段代码实现了一个函数 `findShortestSubArray`,用于找到给定数组中,出现次数最多的数字所对应的最短连续子数组的长度。
具体实现过程如下:
1. 首先定义了三个字典变量:`count`、`first_occurrence` 和 `max_degree`,分别用于统计每个数字出现的频数、第一次出现的位置以及最大度(即出现次数最多的数字的出现次数)。
2. 然后遍历输入的数组 `nums`,对于每个数字 `num`,如果它不在 `count` 中,则将其添加到 `count` 中并记录其第一次出现的位置;否则,将其出现次数加一。同时,如果当前数字的出现次数大于之前的最大度,则更新最大度。
3. 接着遍历 `count` 中的每个数字,如果某个数字的出现次数等于最大度,则计算该数字所对应的最短连续子数组的长度。具体来说,首先计算该数字最后一次出现的位置与第一次出现的位置之差加一,即为该数字所对应的子数组的长度;然后将这个长度与之前计算得到的最短连续子数组长度进行比较,取较小值作为新的最短连续子数组长度。
4. 最后返回计算得到的最短连续子数组长度。
需要注意的是,在计算最短连续子数组长度时,需要使用变量 `i` 来记录当前遍历到的位置,因此在循环开始前需要先初始化 `i` 为 0。
三、解题方法二
def findShortestSubArray(nums):
# 使用哈希表记录每个数字出现的次数和位置
count = {}
for i, num in enumerate(nums):
if num not in count:
count[num] = [1, i]
else:
count[num][0] += 1# 按照出现次数从大到小排序
sorted_count = sorted(count.items(), key=lambda x: x[1][0], reverse=True)# 找到出现次数最多的数字所对应的最短连续子数组长度
max_degree = sorted_count[0][1][0]
min_length = float('inf')for num, (degree, _) in enumerate(sorted_count):if degree == max_degree:length = nums[_] + nums[_ + degree] + 1if length < min_length:min_length = lengthreturn min_length这个实现方式与之前的实现方式类似,但是使用了哈希表来记录每个数字出现的次数和位置,避免了在遍历数组时多次计算某个数字的出现次数。同时,将哈希表中的元素按照出现次数从大到小排序,可以减少后续查找的复杂度。最后,通过遍历排序后的哈希表,找到出现次数最多的数字所对应的最短连续子数组长度。
相关文章:

打卡力扣题目十二
#左耳听风 ARST 打卡活动重启# 目录 一、问题 二、解题方法一 三、解题方法二 关于 ARTS 的释义 —— 每周完成一个 ARTS: ● Algorithm: 每周至少做一个 LeetCode 的算法题 ● Review: 阅读并点评至少一篇英文技术文章 ● Tips: 学习至少一个技术技巧 ● Share: …...

QT服务器练习
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//给服务器指针实例化空间server new QTcpServer(this); }Widget::~Widget() {delete ui; }//启动服务器按钮对…...
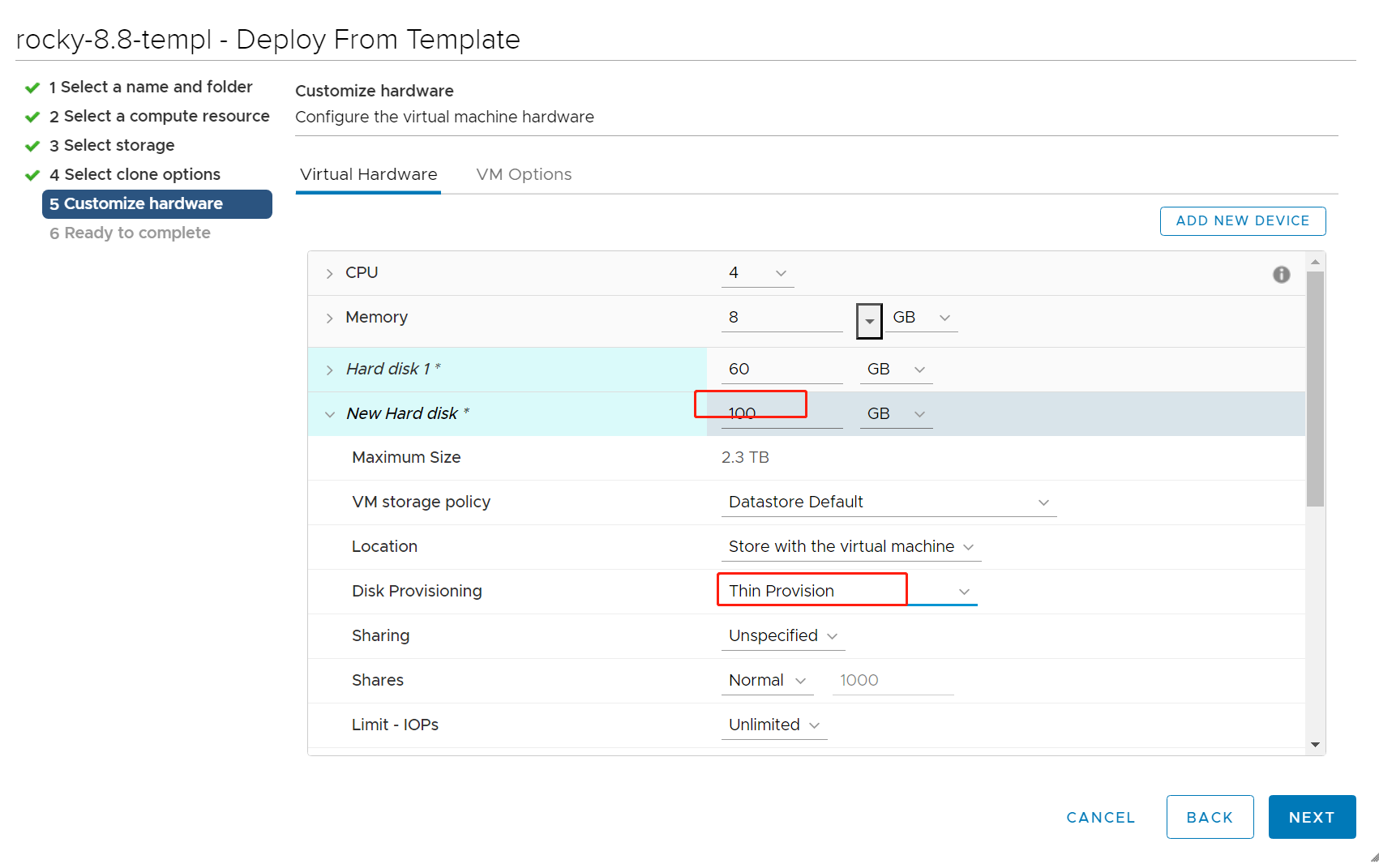
Vcenter 创建 虚拟机配置 Thin Provision 模式 disk
介绍 在vCenter中选择虚拟磁盘格式通常也取决于您的需求和使用情况。 vSphere支持多种虚拟磁盘格式,以下是一些常见的格式: Thick Provision Lazy Zeroed:这是vSphere中的默认格式。它会预分配虚拟磁盘所需的存储空间,但只有在虚…...
初识mysql数据库之事务的概念及操作
目录 一、数据库多客户端访问问题 1. 数据库的CURD无限制带来的问题 2. 如何解决CURD导致的问题 二、事务的概念 1. 什么是事务 2. 事务的四个属性 3. mysql对事务的管理 4. 为什么会有事务 5. 事务的版本支持 三、事务的操作 1. 事务提交方式 2. 事务操作的准备工…...
)
MPL-2.0(Mozilla Public License 2.0)
MPL-2.0(Mozilla Public License 2.0)是一种开源软件许可证,由 Mozilla 组织于2012年发布,用于授权开源项目。MPL-2.0 是 MPL-1.1 许可证的继任版本,旨在更好地适应现代开源软件的发展和使用。 MPL-2.0 许可证的主要特…...

Qt+OpenCV+VTK在VS2017中配置路径
QtOpenCVVTK在VS2017中配置路径 《Qt环境配置》《OpenCV环境配置》《VTK环境配置》 《Qt环境配置》 包含目录: D:\Qt\Qt5.12.11\5.12.11\msvc2017_64\include D:\Qt\Qt5.12.11\5.12.11\msvc2017_64\include\QtWidgets D:\Qt\Qt5.12.11\5.12.11\msvc2017_64\include…...

线性代数(应用篇):第五章:特征值与特征向量、第六章:二次型
文章目录 第5章 特征值与特征向量、相似矩阵(一) 特征值与特征向量1.定义2.性质3.求解(1)具体型矩阵试根法、多项式带余除法:三阶多项式分解因式 (2)抽象型矩阵 (二) 相似1.矩阵相似(1)定义(2)性质 2.相似对角化(1)定义(2)相似对角化的条件(n阶矩阵A可相…...

Java8实战-总结9
Java8实战-总结9 Lambda表达式把Lambda付诸实践:环绕执行模式第1步:记得行为参数化第2步:使用函数式接口来传递行为第3步:执行一个行为第4步:传递Lambda 使用函数式接口PredicateConsumerFunction原始类型特化 Lambda表…...

大数据开发面试必问:Hive调优技巧系列一
Hive必问调优 Hive 调优拆解:Hive SQL 几乎是每一位互联网分析师的必备技能,相信很多小伙伴都有被面试官问到 Hive 优化问题的经历。所以掌握扎实的 HQL 基础尤为重要,hive优化也是小伙伴应该掌握的一项技能,本篇文章具体从hive建表优化、HQ…...
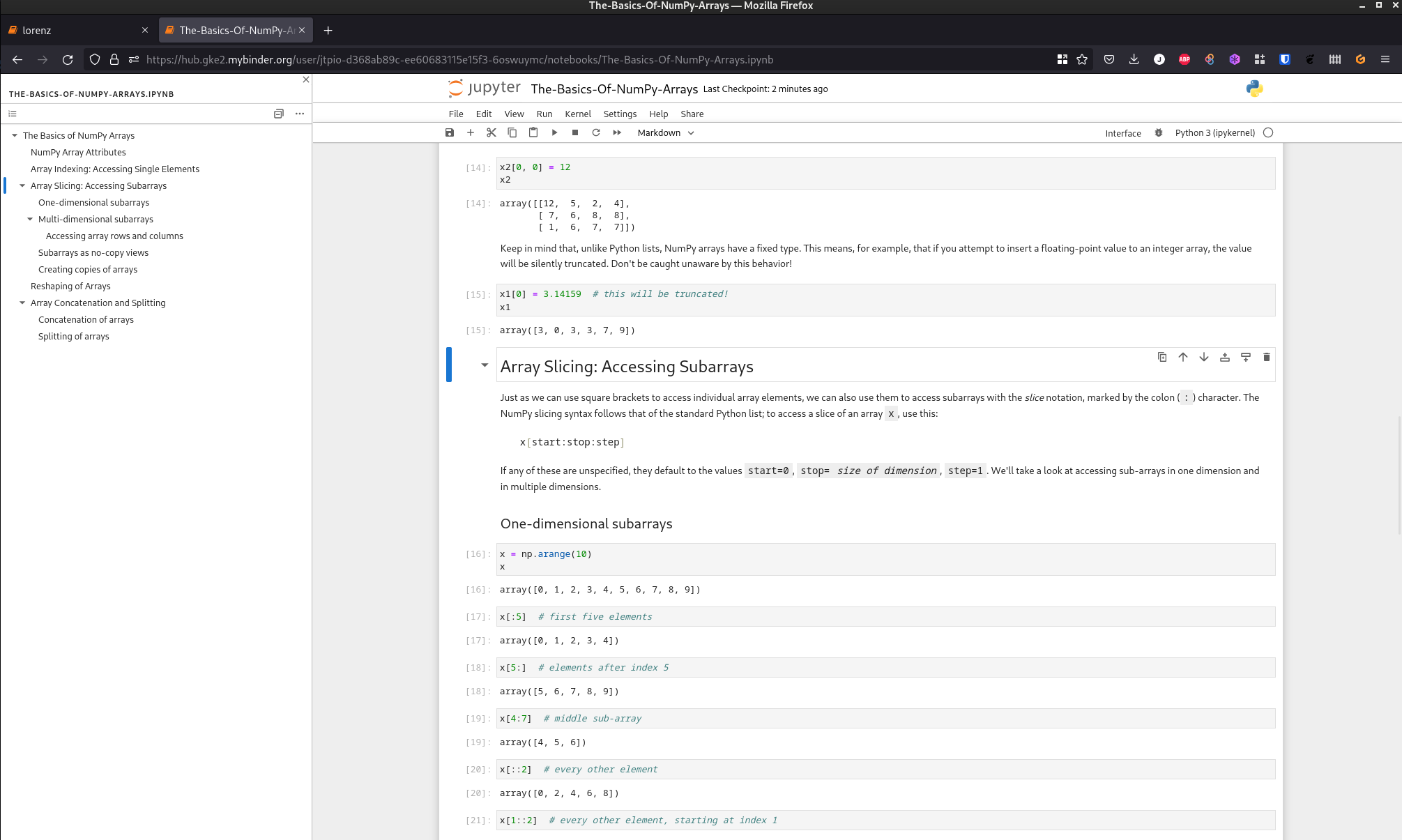
Jupyter Notebook 7重磅发布,新增多个特性!
本文分享Jupyter Notebook大版本v7.0.0更新亮点,及简单测试! 近日,Jupyter Notebook大版本v7.0.0更新,Jupyter Notebook 7基于JupyterLab,因此它包含了过去几年JupyterLab中添加的许多新功能和改进,部分亮…...

linux V4L2子系统——v4l2架构(1)之整体架构
概述 V4L(Video for Linux)是Linux内核中关于视频设备的API接口,涉及视频设备的音频和视频信息采集及处理、视频设备的控制。V4L出现于Linux内核2.1版本,经过修改bug和添加功能,Linux内核2.5版本推出了V4L2(…...
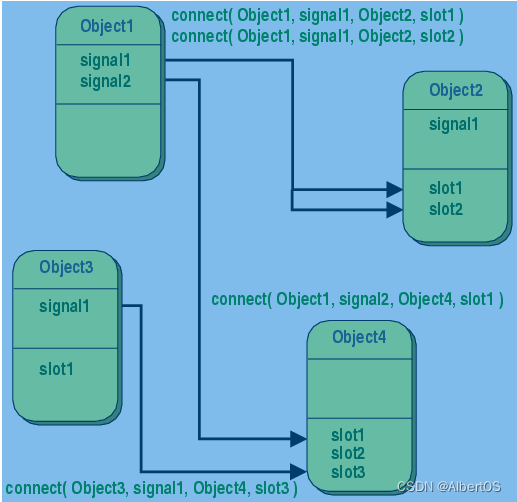
Qt信号与槽机制的本质
引入 对象与对象之间的通信有多个方式,如果我们要提供一种对象之间的通信机制。这种机制,要能够给两个不同对象中的函数建立映射关系,前者被调用时后者也能被自动调用。 再深入一些,两个对象如果都互相不知道对方的存在ÿ…...
Linux:入门学习知识及常见指令
文章目录 入门介绍操作系统的概念Linux机器的使用Linux上的指令 对文件知识的补充文件的定义和一些含义文件和目录的存储绝对路径和相对路径 ls指令pwd指令cd指令touch指令mkdir指令rmdir指令rm指令man指令cp指令mv指令cat指令more指令echo指令输出重定向 less指令find指令grep…...

K8s:Kubernetes 故障排除方法论
写在前面 博文内容为节译整理文中提到的工具大部分是商业软件,不是开源的,作为了解理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它…...
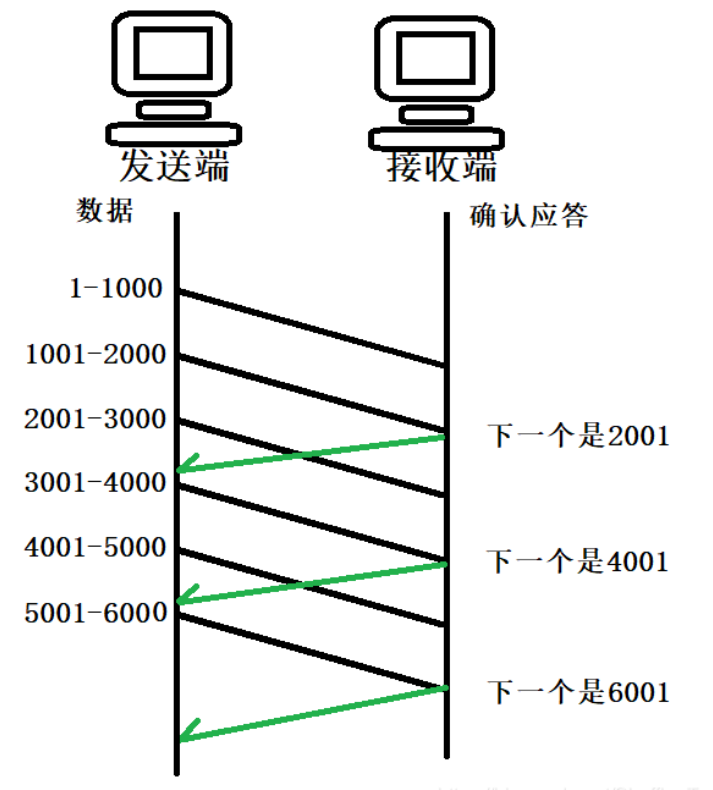
TCP 三次握手四次挥手浅析
大家都知道传输层中的TCP协议是面向连接的,提供可靠的连接服务,其中最出名的就是三次握手和四次挥手。 一、三次握手 三次握手的交互过程如下 喜欢钻牛角尖的我在学习三次握手的时候就想到了几个问题:为什么三次握手是三次?不是…...
【软件安装】MATLAB_R2021b for mac 安装
Mac matlab_r2021b 安装 下载链接:百度网盘 下载链接中所有文件备用。 我所使用的电脑配置: Macbook Pro M1 Pro 16512 系统 macOS 13.5 安装步骤 前置准备 无此选项者,自行百度 “mac 任何来源”。 1 下载好「MATLAB R2021b」安装文…...
电脑维护:10妙招,让你的电脑更加稳定!
你的电脑已经成为你工作、学习、娱乐的最佳工具之一,但是如果你不做好电脑维护工作,就可能面临着电脑变慢、蓝屏、崩溃等问题。在这篇文章中,我们将介绍10个电脑维护步骤,让你的电脑更加稳定! 为什么需要电脑维护&…...

大数据面试题:Kafka的单播和多播
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 参考答案: 1、单播 一条消息只能被某一个消费者消费的模式称为单播。要实现消息单播,只要让这些消费者属于同一个消费者组即…...

python与深度学习(八):CNN和fashion_mnist二
目录 1. 说明2. fashion_mnist的CNN模型测试2.1 导入相关库2.2 加载数据和模型2.3 设置保存图片的路径2.4 加载图片2.5 图片预处理2.6 对图片进行预测2.7 显示图片 3. 完整代码和显示结果4. 多张图片进行测试的完整代码以及结果 1. 说明 本篇文章是对上篇文章训练的模型进行测…...
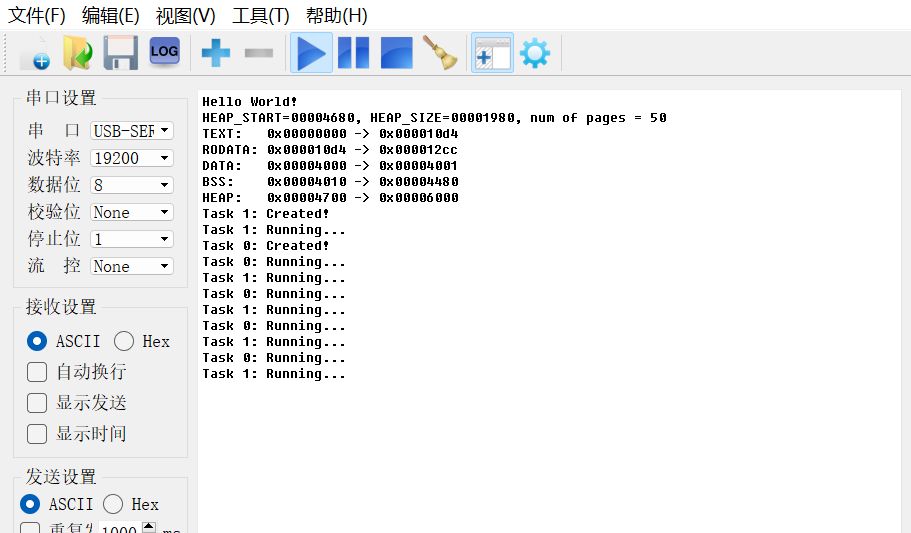
开发一个RISC-V上的操作系统(五)—— 协作式多任务
目录 往期文章传送门 一、什么是多任务 二、代码实现 三、测试 往期文章传送门 开发一个RISC-V上的操作系统(一)—— 环境搭建_riscv开发环境_Patarw_Li的博客-CSDN博客 开发一个RISC-V上的操作系统(二)—— 系统引导程序&a…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
