算法leetcode|64. 最小路径和(rust重拳出击)
文章目录
- 64. 最小路径和:
- 样例 1:
- 样例 2:
- 提示:
- 分析:
- 题解:
- rust:
- go:
- c++:
- python:
- java:
64. 最小路径和:
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
样例 1:
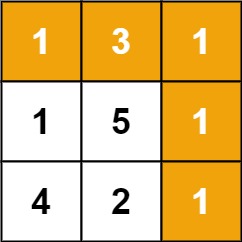
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]输出:7解释:因为路径 1→3→1→1→1 的总和最小。
样例 2:
输入:grid = [[1,2,3],[4,5,6]]输出:12
提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 200
- 0 <= grid[i][j] <= 200
分析:
- 面对这道算法题目,二当家的再次陷入了沉思。
- 这道题和62. 不同路径和63. 不同路径 II 有些类似,但是这次是寻找最优解,由于每个位置的数值不一定是多少,所以同样没法使用数学公式直接计算。
- 那么动态规划又成了此时的优选。
- 从左上角出发,网格的第一行的每个元素只能从左上角元素开始向右移动到达,网格的第一列的每个元素只能从左上角元素开始向下移动到达,此时的路径是唯一的,因此每个元素对应的最小路径和即为对应的路径上的数字总和。
- 其他的点只能从上或者从左到达,所以一个点的最优路径,一定经过上面或者左面。从上到下,从左到右开始动态规划,分解成了子问题。到达当前点的最短路径和,就是上面和左面点的最小路径和中的较小值加上当前点的值。
- 这里一样可以使用滚动数组优化空间。
题解:
rust:
impl Solution {pub fn min_path_sum(grid: Vec<Vec<i32>>) -> i32 {let (rows, cols) = (grid.len(), grid[0].len());let mut dp = vec![0; cols];dp[0] = grid[0][0];(1..cols).for_each(|c| {dp[c] = dp[c - 1] + grid[0][c];});(1..rows).for_each(|r| {dp[0] += grid[r][0];(1..cols).for_each(|c| {dp[c] = dp[c].min(dp[c - 1]) + grid[r][c];});});return dp[cols - 1];}
}
go:
func minPathSum(grid [][]int) int {rows, cols := len(grid), len(grid[0])dp := make([]int, cols)dp[0] = grid[0][0]for c := 1; c < cols; c++ {dp[c] = dp[c-1] + grid[0][c]}for r := 1; r < rows; r++ {dp[0] += grid[r][0]for c := 1; c < cols; c++ {if dp[c-1] < dp[c] {dp[c] = dp[c-1] + grid[r][c]} else {dp[c] += grid[r][c]}}}return dp[cols-1]
}
c++:
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {const int rows = grid.size(), cols = grid[0].size();int dp[cols];dp[0] = grid[0][0];for (int c = 1; c < cols; ++c) {dp[c] = dp[c - 1] + grid[0][c];}for (int r = 1; r < rows; ++r) {dp[0] += grid[r][0];for (int c = 1; c < cols; ++c) {dp[c] = min(dp[c], dp[c - 1]) + grid[r][c];}}return dp[cols - 1];}
};
python:
class Solution:def minPathSum(self, grid: List[List[int]]) -> int:rows, cols = len(grid), len(grid[0])dp = [0] * colsfor c in range(cols):dp[c] = dp[c - 1] + grid[0][c]for r in range(1, rows):dp[0] += grid[r][0]for c in range(1, cols):dp[c] = min(dp[c], dp[c - 1]) + grid[r][c]return dp[cols - 1]java:
class Solution {public int minPathSum(int[][] grid) {final int rows = grid.length, cols = grid[0].length;final int[] dp = new int[cols];dp[0] = grid[0][0];for (int c = 1; c < cols; ++c) {dp[c] = dp[c - 1] + grid[0][c];}for (int r = 1; r < rows; ++r) {dp[0] += grid[r][0];for (int c = 1; c < cols; ++c) {dp[c] = Math.min(dp[c], dp[c - 1]) + grid[r][c];}}return dp[cols - 1];}
}
非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~
相关文章:

算法leetcode|64. 最小路径和(rust重拳出击)
文章目录 64. 最小路径和:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 64. 最小路径和: 给定一个包含非负整数的 m x n 网…...
的效果)
css---实现文本超过两行时显示省略号(...)的效果
可以使用CSS中的text-overflow属性配合-webkit-line-clamp属性来实现。以下是一种常见的方式: .text-container {overflow: hidden;display: -webkit-box;-webkit-line-clamp: 2; /* 设置最大显示行数 */-webkit-box-orient: vertical;text-overflow: ellipsis; }在…...
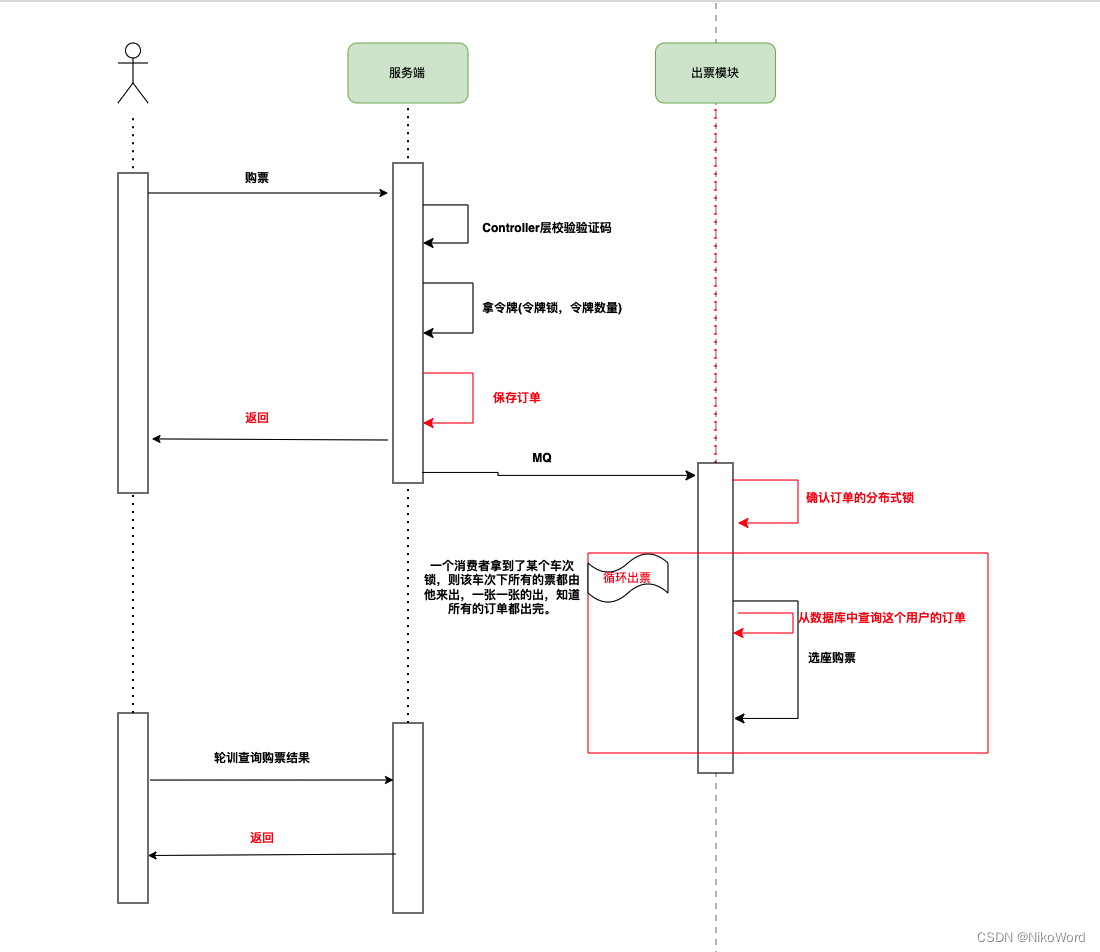
30-使用RocketMQ做削峰处理
1、增加排队功能的思路 在出票模块里,一个消费者拿到了某个车次锁,则该车次下所有的票都由他来出,一张一张的出,知道所有的订单都出完。 2、实现排队出票功能 2.1、 修改发送到MQ消息的内容 修改MQ消息内容,只需要通知出哪天和哪个车次的票(即:组成锁的内容),不需要…...

如何用非root账号安装k8s集群
在大多数情况下,为了安装 Kubernetes(K8s)集群,需要具有root权限或者以root身份执行某些操作,例如安装软件包和配置系统级别的设置。然而,你可以通过以下方法在非root账号下安装K8s集群: 使用Mi…...
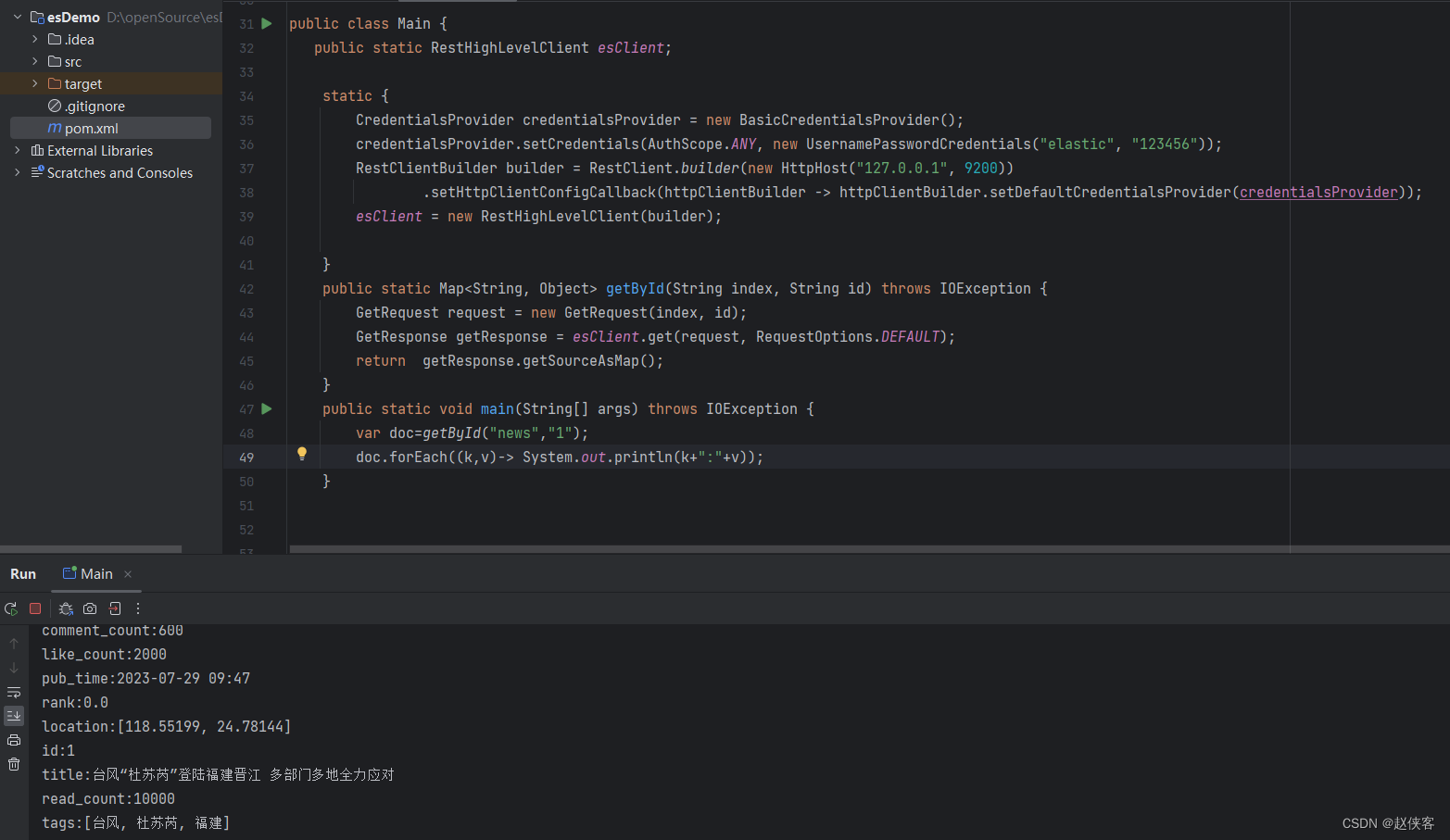
windows环境安装elasticsearch+kibana并完成JAVA客户端查询
下载elasticsearch和kibana安装包 原文连接:https://juejin.cn/post/7261262567304298554 elasticsearch官网下载比较慢,有时还打不开,可以通过https://elasticsearch.cn/download/下载,先找到对应的版本,最好使用迅…...

高精度算法
基础模板: (411条消息) 高精度加法_会笑的小熊的博客-CSDN博客 (411条消息) 高精度乘法_会笑的小熊的博客-CSDN博客 (411条消息) 高精度减法_会笑的小熊的博客-CSDN博客 目录 P1601 AB Problem(高精) P1303 A*B Problem P1009 [NOIP1998 普…...
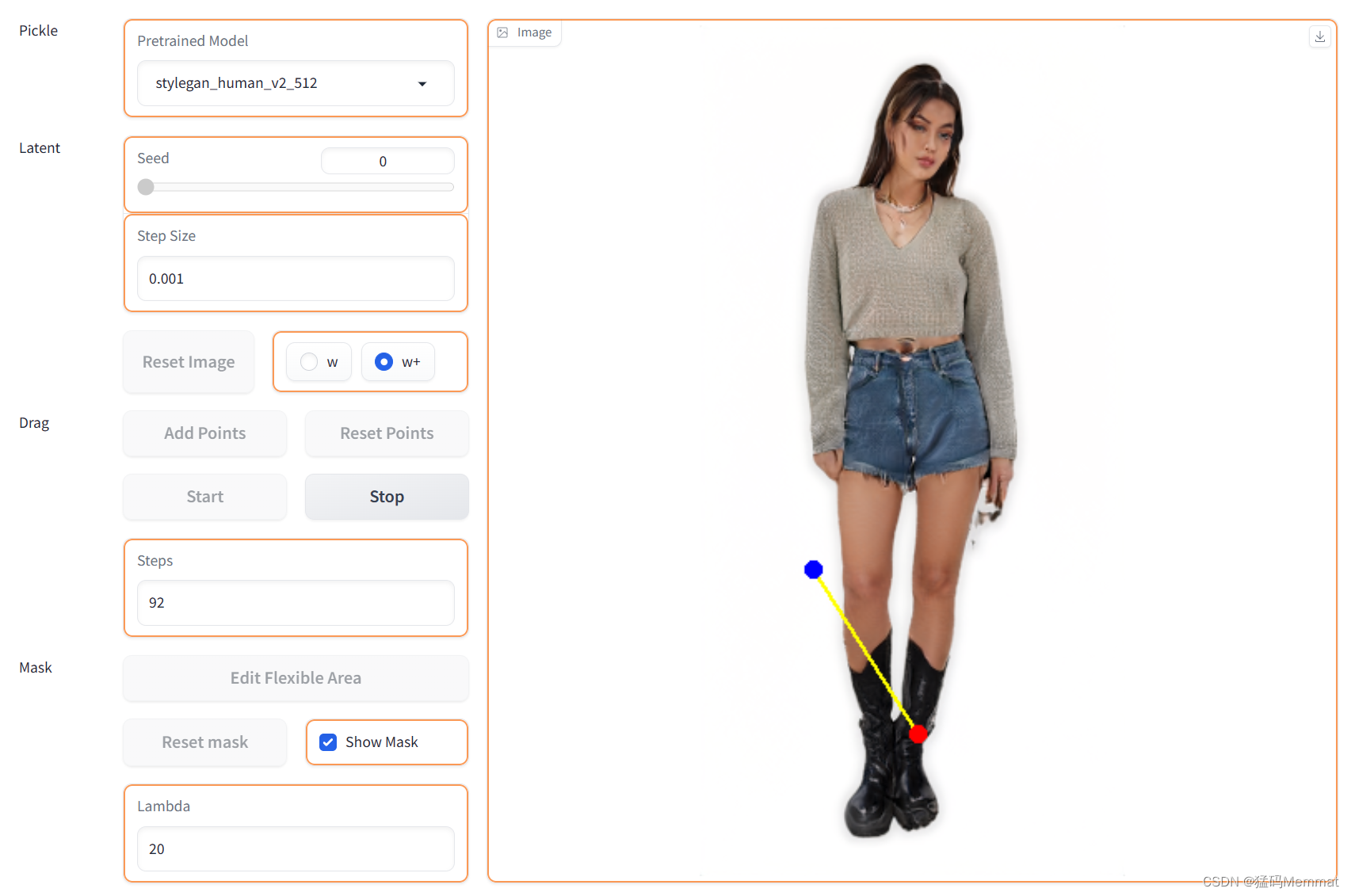
DragGAN:用崭新的方式进行图像处理
该项目的论文被SIGGRAPH 2023 收录,论文以 StyleGAN2 架构为基础,实现了 “Drag” 关键点就能轻松 P 图的效果。 https://github.com/XingangPan/DragGAN https://vcai.mpi-inf.mpg.de/projects/DragGAN/ 目录 原图1测试一测试二测试三 原图2测试一测试…...

语音播放 linux
调整语音音量大小 pactl list sinks pactl set-sink-volume 15 12345 # 15可以改成别的id安装pip install pyttsx3 sudo apt-get update sudo apt-get install espeak sudo ldconfig pip3 install pyttsx3代码 import pyttsx3 import threading def speak_work(text):engine…...

各大互联网公司面经分享:Java 全栈知识 +1500 道大厂面试真题
这篇文章给大家分享一下我遇到的一些质量较高的面试经历,具体经过就不多说了,就把面试题打出来供各位读者老哥参考如有不全的地方,各位海涵。 猿辅导 八皇后问题 求二叉树的最长距离(任意两个节点的路径 中最长的) lru 算法的实现 设计一…...
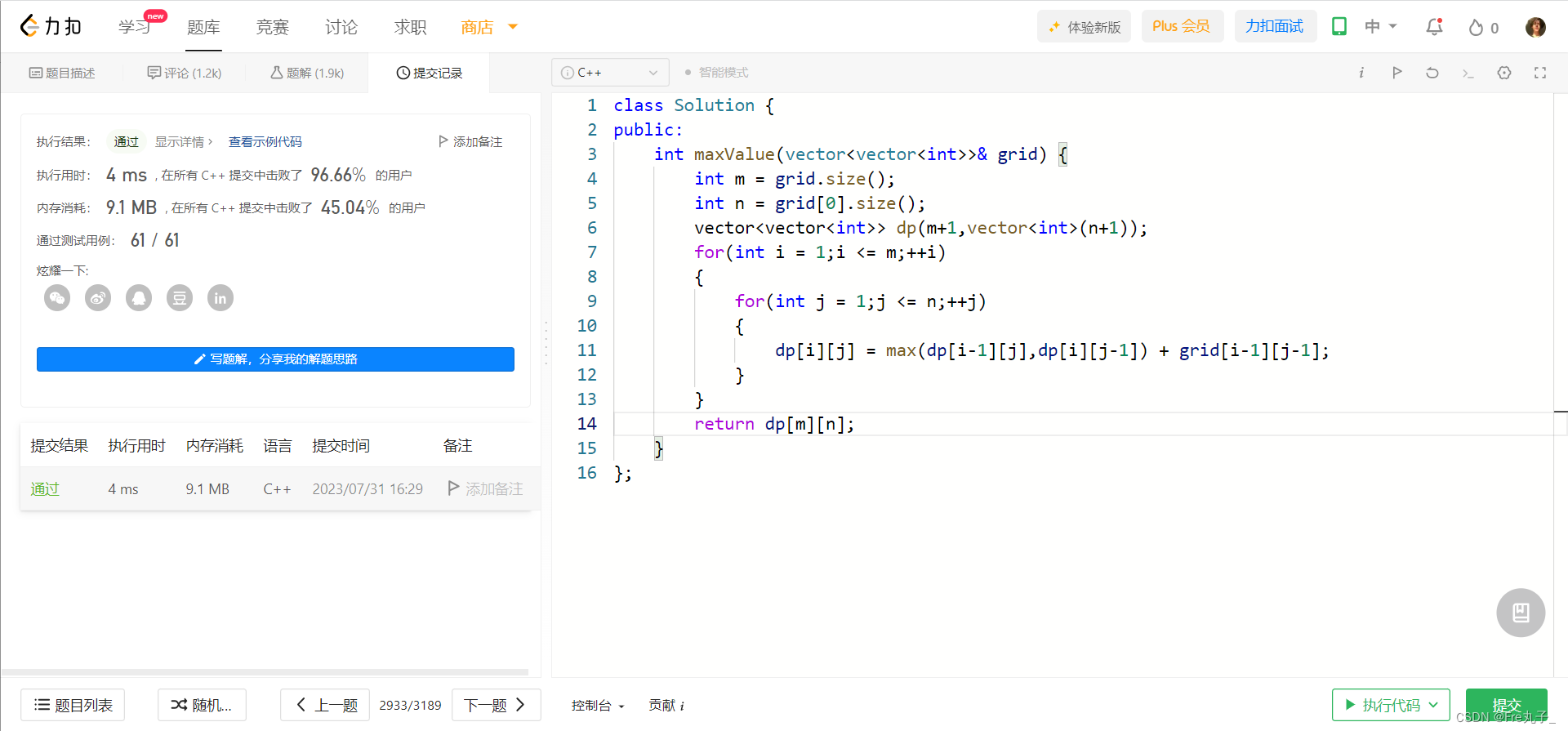
【LeetCode】剑指offer礼物的最大价值
礼物的最大价值 题目描述算法分析编程代码 链接: 礼物的最大价值 题目描述 算法分析 编程代码 class Solution { public:int maxValue(vector<vector<int>>& grid) {int m grid.size();int n grid[0].size();vector<vector<int>> dp(m1,vector…...

应用层协议——https
文章目录 1. HTTPS 是什么2. 什么是"加密"3. 常见的加密方式4. 数据摘要 && 数字签名5. HTTPS 的工作过程探究5.1 方案1 - 只使用对称加密5.2 方案2 - 只使用非对称加密5.3 方案3 - 双方都使用非对称加密5.4 方案4 - 非对称加密 对称加密5.5 中间人攻击5.6 …...

Emacs之实现鼠标/键盘选中即拷贝外界内容(一百二十)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

智慧城市环境污染数据采集远程监控方案4G工业路由器应用
随着科技水平的发展和人民生活水平的提高,城市环境污染问题日渐严峻,尤其是在发展迅速的国家,环境污染问题便更为突出。许多发达国家将重污染工厂搬到发展中国家,这导致发展中国家的环境污染日益严重。严重的环境污染也带来了一系…...

大数据技术之Clickhouse---入门篇---安装
星光下的赶路人star的个人主页 努力到无能为力,拼搏到感动自己 文章目录 1、ClickHouse的安装1.1 准备工作1.1.1 确定防火墙处于关闭状态1.1.2 CentOS取消打开文件数限制1.1.3 安装依赖(所有节点都进行依赖安装)1.1.4 CentOS取消SELINUX 1.2 …...
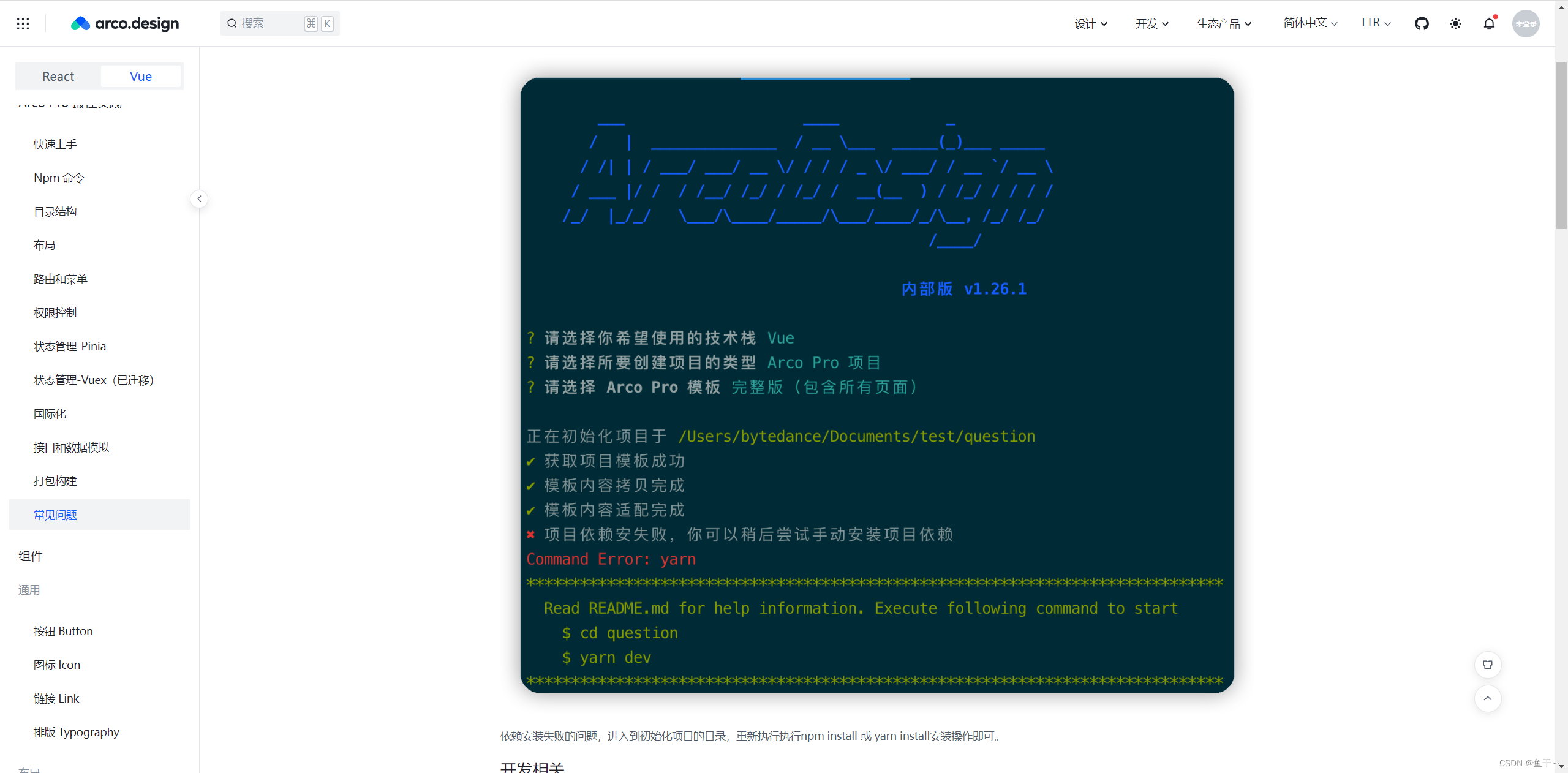
vue3搭建Arco design UI框架
技术:Vue3.2.40 UI框架:Arco design 2.44.7 需要安装:yarn 1.22.19 和npm 8.19.4 1.第一步安装本地全局arco脚手架 管理员运行CMD npm i -g arco-cli安装成功后如下: 2.第二步在需要存放项目的文件夹拉取项目 我这里把项目存放在 D:\W…...
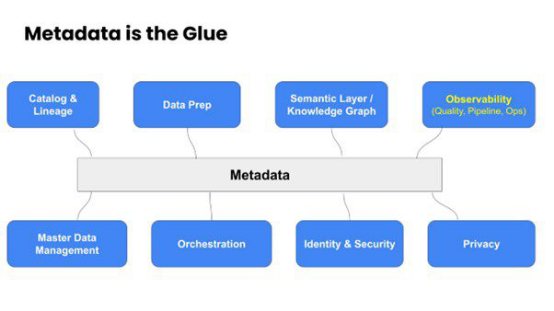
提升数据质量的四大有效方式
在数字时代的今天,企业对于高质量、值得信赖的数据的需求越来越高。 目前,已经有很多企业将数据质量视为技术问题而非业务问题,这也是获取高质量数据的最大限制因素。只有查找技术缺陷,例如重复数据、缺失值、乱序序列࿰…...
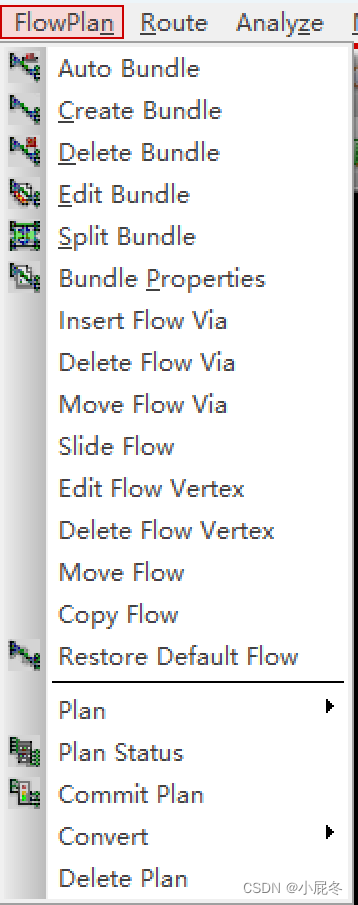
ALLEGRO之FlowPlan
本文主要讲述了ALLEGRO的FlowPlan菜单。 (1)Auto Bundle:暂不清楚; (2)Create Bundle:暂不清楚; (3)Delete Bundle:暂不清楚; &…...

Python - OpenCV实现摄像头人脸识别(亲测版)
要使用Python 3和OpenCV进行摄像头人脸识别,您可以按照以下步骤进行操作: 0.安装OpenCV软件 去官网直接下载安装即可,如果是C使用OpenCV,需要使用编译源码并配置环境变量。 1.安装OpenCV库 在命令行中输入以下命令: pip inst…...

date日期相关操作汇总
一、若表中date字段存储形式为:2021-05-16 在表中找到2021年8月份数据的方法 方法1. like 语法:where date like 2021-08%; 前面能匹配上的就是2021年8月份。 方法2. year,month函数(mysql中有,oracle中不确定) 语法&…...

生产者-消费者模式
文章目录 一、生产者-消费者模式的应用场景1、Excutor任务执行框架:2、消息中间件active MQ:3、任务的处理时间比较长的情况下:二、生产者-消费者模式的优点1、优点:2、缺点:二、C++实现生产者-消费者模型1、依赖2、实现细节3、问题4、核心代码生产者-消费者模式是一个十分…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...

【中间件】Web服务、消息队列、缓存与微服务治理:Nginx、Kafka、Redis、Nacos 详解
Nginx 是什么:高性能的HTTP和反向代理Web服务器。怎么用:通过配置文件定义代理规则、负载均衡、静态资源服务等。为什么用:提升Web服务性能、高并发处理、负载均衡和反向代理。优缺点:轻量高效,但动态处理能力较弱&am…...

Go 语言中的内置运算符
1. 算术运算符 注意: (自增)和--(自减)在 Go 语言中是单独的语句,并不是运算符。 package mainimport "fmt"func main() {fmt.Println("103", 103) // 13fmt.Println("10-3…...
