常微分方程建模R包ecode(二)——绘制相速矢量场
本节中我们考虑一个更为复杂的常微分方程模型,
d X C d t = ν ( X A + Y A ) − β ⋅ X C ⋅ ( Y C + Y A ) − ( μ + g ) ⋅ X C , ( 1 ) d Y C d t = β ⋅ X C ⋅ ( Y C + Y A ) − ( μ + g + ρ ) ⋅ Y C , ( 2 ) d X A d t = g ⋅ X C − β ⋅ X A ⋅ ( Y C + Y A ) , ( 3 ) d Y A d t = β ⋅ X A ∗ ( Y C + Y A ) + g ∗ Y C − ρ ∗ Y A ( 4 ) \frac{dX_C}{dt} = \nu (X_A + Y_A) - \beta · X_C · (Y_C + Y_A) - (\mu + g) · X_C, \quad(1) \\ \frac{dY_C}{dt} = \beta · X_C · (Y_C + Y_A) - (\mu + g + \rho) · Y_C, \quad(2)\\ \frac{dX_A}{dt} = g · X_C - \beta · X_A · (Y_C + Y_A), \quad (3) \\ \frac{dY_A}{dt} = \beta · X_A * (Y_C + Y_A) + g * Y_C - \rho * Y_A \quad(4) dtdXC=ν(XA+YA)−β⋅XC⋅(YC+YA)−(μ+g)⋅XC,(1)dtdYC=β⋅XC⋅(YC+YA)−(μ+g+ρ)⋅YC,(2)dtdXA=g⋅XC−β⋅XA⋅(YC+YA),(3)dtdYA=β⋅XA∗(YC+YA)+g∗YC−ρ∗YA(4)
该常微分方程系统用于模拟一种树木传染病动态,其中 X C X_C XC代表易感树苗(susceptible sapling)的个体数, Y C Y_C YC代表感病树苗(infected sapling)的个体数, X A X_A XA代表易感成年树木的个体数(susceptible adult), Y A Y_A YA代表感病成年树木(infected adult)的个体数。显然 X C , Y C , X A , Y A ≥ 0 X_C,Y_C,X_A,Y_A≥0 XC,YC,XA,YA≥0。
( 1 ) (1) (1)式中, ν ( X A + Y A ) \nu (X_A + Y_A) ν(XA+YA)代表繁殖产生新树苗的速率,其中 ν \nu ν是繁殖速率。 − β ⋅ X C ⋅ ( Y C + Y A ) -\beta · X_C · (Y_C + Y_A) −β⋅XC⋅(YC+YA)指的是由于疾病传染,导致易感树苗转化为感病树苗的速率,其中 β \beta β为传染率。 − ( μ + g ) ⋅ X C , - (\mu + g) · X_C, −(μ+g)⋅XC,是指由于自然死亡及树木成长,导致易感树苗被移除,或是进入到易感成年树木的速率,其中 μ \mu μ为自然死亡率, g g g为树木生长率。
( 2 ) (2) (2)式中, β ⋅ X C ⋅ ( Y C + Y A ) \beta · X_C · (Y_C + Y_A) β⋅XC⋅(YC+YA)代表由易感树苗被传染而转化为感病树苗的速率, − ( μ + g + ρ ) ⋅ Y C - (\mu + g + \rho) · Y_C −(μ+g+ρ)⋅YC则包含自然死亡、树木成长、因疾病感染而死亡这三个过程,其中 ρ \rho ρ代表由于传染病而导致的死亡率。
( 3 ) (3) (3)式中, g ⋅ X C g · X_C g⋅XC代表由于树木生长而使易感树苗转换为易感成年树木的速率, − β ⋅ X A ⋅ ( Y C + Y A ) - \beta · X_A · (Y_C + Y_A) −β⋅XA⋅(YC+YA)代表由于疾病传染,使易感成年大树转换为感病成年大树的速率。
( 4 ) (4) (4)式中, β ⋅ X A ∗ ( Y C + Y A ) \beta · X_A * (Y_C + Y_A) β⋅XA∗(YC+YA)对应于疾病传染过程, g ∗ Y C g * Y_C g∗YC对应于树木生长过程, − ρ ∗ Y A -\rho * Y_A −ρ∗YA对应于疾病导致的死亡过程。
研究一个常微分方程系统,最为直接的方法是研究其相速矢量场(phase velocity vector filed)。下面我们回顾一下与相速矢量场相关的几个重要概念,
常微分方程中的几个重要概念
相空间(phase space):是指所有模型变量的所有可能取值的组合构成的空间。在本节案例中,相空间为 { ( X C , Y C , X A , Y A ) ∣ X C , Y C , X A , Y A ≥ 0 } \{(X_C,Y_C,X_A,Y_A)| X_C,Y_C,X_A,Y_A≥0\} {(XC,YC,XA,YA)∣XC,YC,XA,YA≥0}。
相点(phase point):相空间中的任意一个点称为相点。相点用于描述系统的状态。在本节案例中,相点 ( X C , Y C , X A , Y A ) = ( 10 , 60 , 20 , 100 ) (X_C,Y_C,X_A,Y_A)=(10,60,20,100) (XC,YC,XA,YA)=(10,60,20,100)代表系统中有10棵易感树苗、60棵感病树苗、20棵易感成树、100棵感病成树。
相速矢量(phase velocity vector):系统位于某一相点时,其速度大小和方向构成的矢量,叫做该相点所对应的相速矢量。在本节案例中,针对相点 ( X C , Y C , X A , Y A ) = ( 10 , 60 , 20 , 100 ) (X_C,Y_C,X_A,Y_A)=(10,60,20,100) (XC,YC,XA,YA)=(10,60,20,100),将 X C , Y C , X A , Y A X_C,Y_C,X_A,Y_A XC,YC,XA,YA的值代入式 ( 1 − 4 ) (1-4) (1−4),求出 ( d X C d t , d Y C d t , d X A d t , d Y A d t ) (\frac{dX_C}{dt}, \frac{dY_C}{dt} , \frac{dX_A}{dt} , \frac{dY_A}{dt}) (dtdXC,dtdYC,dtdXA,dtdYA),其值便是该相点所对应的相速矢量。相速矢量描述了系统位于某一相点时的运动方向和快慢。
相速矢量场(phase velocity vector field):相空间中所有相速矢量组成的集合。
相位曲线(phase curve):相点沿相速矢量场移动所形成的运动轨迹。
在ecode包中,当函数plot作用于eode类的对象时,plot函数会自动绘制出某个常微分方程系统的相速矢量场,或相速矢量。在上一节中,我们介绍了当常微分方程系统中含有两个模型变量时,plot函数的用法。
本节所关注的模型含有四个模型变量 X C , Y C , X A , Y A X_C,Y_C,X_A,Y_A XC,YC,XA,YA,因而将介绍含有多个模型变量时,plot函数的行为。
一、绘制相速矢量场
首先我们在ecode包中构建上述模型(式 ( 1 − 4 ) (1-4) (1−4)):
library(ecode)dX_Cdt <- function(X_C, Y_C, X_A, Y_A, nu = 0.15, beta = 0.1, mu = 0.15, g = 0.04)nu * (X_A + Y_A) - beta * X_C * (Y_C + Y_A) - (mu + g) * X_CdY_Cdt <- function(X_C, Y_C, Y_A, beta = 0.1, mu = 0.15, g = 0.04, rho = 0.2)beta * X_C * (Y_C + Y_A) - (mu + g + rho) * Y_CdX_Adt <- function(X_C, Y_C, X_A, Y_A, beta = 0.1, g = 0.04)g * X_C - beta * X_A * (Y_C + Y_A)dY_Adt <- function(X_A, Y_C, Y_A, beta = 0.1, g = 0.04, rho = 0.2)beta * X_A * (Y_C + Y_A) + g * Y_C - rho * Y_Ax <- eode(dX_Cdt = dX_Cdt, dY_Cdt = dY_Cdt, dX_Adt = dX_Adt, dY_Adt = dY_Adt)
x
### An ODE system: 4 equations
### equations:
### dX_Cdt = nu * (X_A + Y_A) - beta * X_C * (Y_C + Y_A) - (mu + g) * X_C
### dY_Cdt = beta * X_C * (Y_C + Y_A) - (mu + g + rho) * Y_C
### dX_Adt = g * X_C - beta * X_A * (Y_C + Y_A)
### dY_Adt = beta * X_A * (Y_C + Y_A) + g * Y_C - rho * Y_A
### variables: X_C Y_C X_A Y_A
### parameters: nu = 0.15, beta = 0.1, mu = 0.15, g = 0.04, rho = 0.2
### constraints: X_A<1000 X_A>0 X_C<1000 X_C>0 Y_A<1000 Y_A>0 Y_C<1000 Y_C>0
由于我们没有在模型中指定模型变量的范围,ecode包自动将变量范围设置在 ( 0 , 1000 ) (0,1000) (0,1000)内。此时调用plot函数,
plot(x)
### Set X_A = 500, Y_A = 500 for mapping in two axis
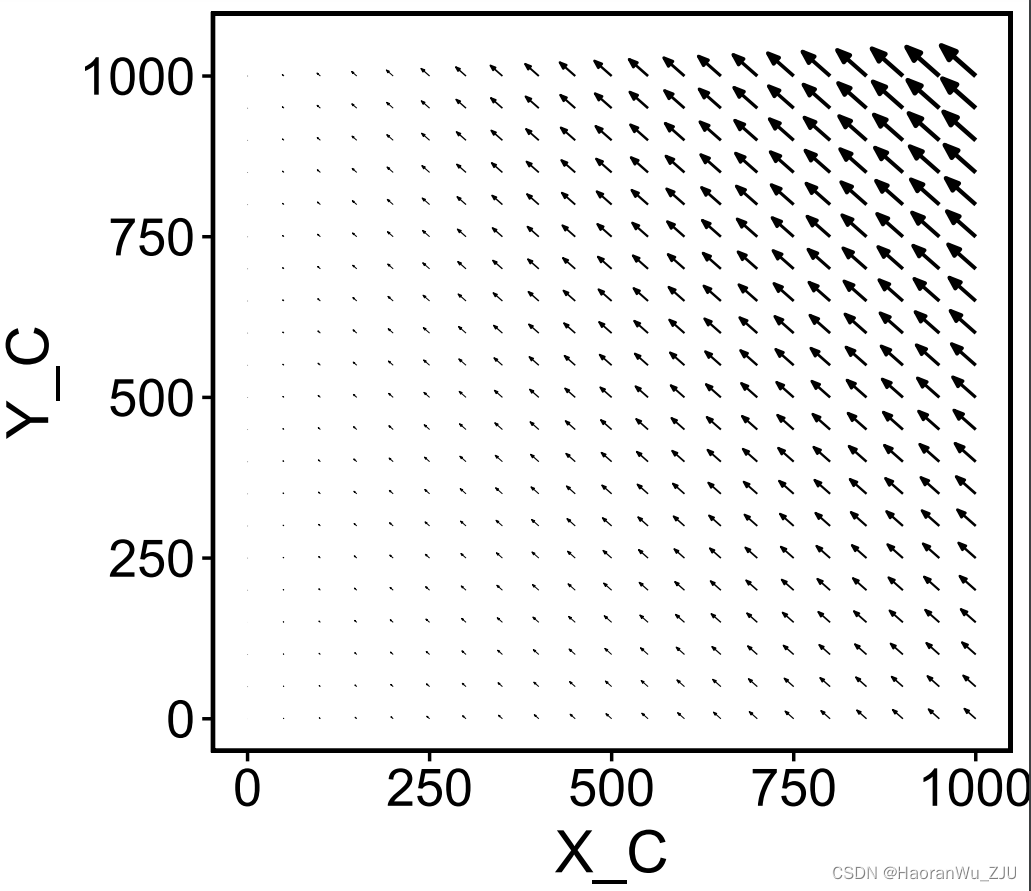
输出结果如图所示。plot函数自动限制了 X A = 500 , Y A = 500 X_A = 500, Y_A = 500 XA=500,YA=500,并以 X C , Y C X_C, Y_C XC,YC为横、纵坐标系绘制相速矢量场。需要注意的是,该相速矢量图仅仅表示 X A , Y A X_A,Y_A XA,YA为固定值时的相速矢量场,该矢量场位于相空间内部的一个平面。
当常微分方程组含有多个模型变量时,如果不给
plot任何参数,则plot函数默认会以常微分方程中前两个变量为坐标轴绘制相速矢量场,而其余变量将会被赋上一个固定值,其值等于该模型变量范围的中值。
二、自定义模型变量的值
如果不希望以 X A = 500 , Y A = 500 X_A = 500, Y_A = 500 XA=500,YA=500为限制条件,则可以在plot函数中添加set_covar参数,
plot(x, set_covar = list(X_A = 10, Y_A = 20))
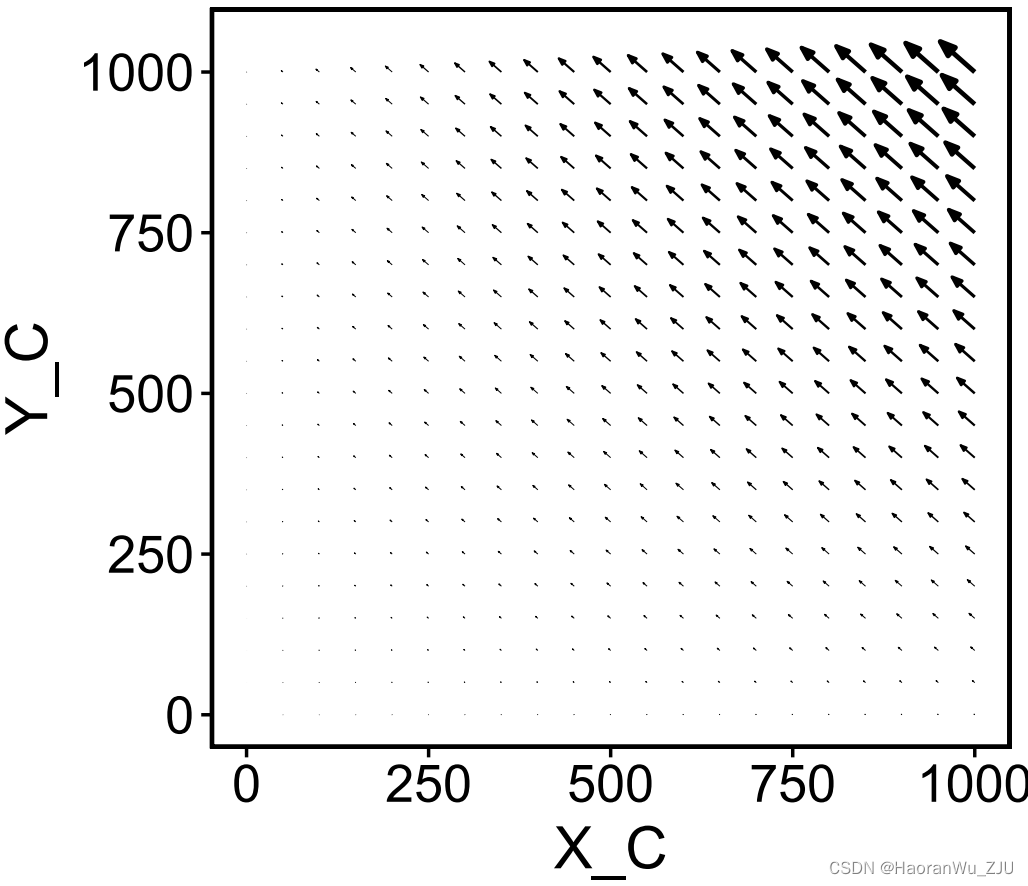 此时,
此时,plot函数给出的是 X A = 10 , Y A = 20 X_A=10, Y_A=20 XA=10,YA=20株时,以 X C , Y C X_C,Y_C XC,YC为坐标轴作出的相速矢量场。
如果想要固定 X C , Y C X_C, Y_C XC,YC,以 X A , Y A X_A, Y_A XA,YA为坐标轴作相速矢量场,则
plot(x, set_covar = list(X_C = 10, Y_C = 20))
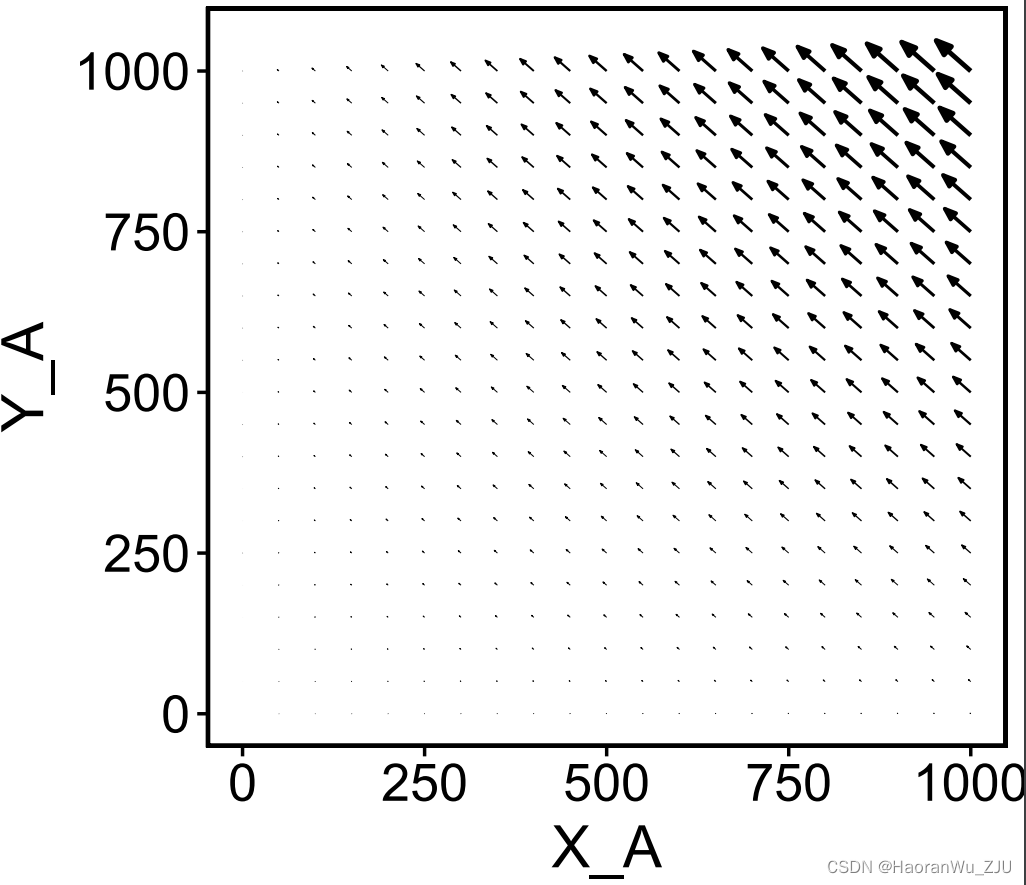
此为 X C = 10 , Y C = 20 X_C=10, Y_C=20 XC=10,YC=20时,以 X A , Y A X_A, Y_A XA,YA为坐标轴的相速矢量场。
三、自定义模型变量的范围
上一节中已经提到,可以采用eode_set_constraint重新设置模型变量的范围。例如,以下代码将 X C , Y C , X A , Y A X_C, Y_C, X_A, Y_A XC,YC,XA,YA的范围位置为 ( 0 , 5 ) (0,5) (0,5),
x <- eode_set_constraint(x, new_constraint = c("X_C<5","Y_C<5","X_A<5","Y_A<5"))
x
### An ODE system: 4 equations
### equations:
### dX_Cdt = nu * (X_A + Y_A) - beta * X_C * (Y_C + Y_A) - (mu + g) * X_C
### dY_Cdt = beta * X_C * (Y_C + Y_A) - (mu + g + rho) * Y_C
### dX_Adt = g * X_C - beta * X_A * (Y_C + Y_A)
### dY_Adt = beta * X_A * (Y_C + Y_A) + g * Y_C - rho * Y_A
### variables: X_C Y_C X_A Y_A
### parameters: nu = 0.15, beta = 0.1, mu = 0.15, g = 0.04, rho = 0.2
### constraints: X_A<5 X_A>0 X_C<5 X_C>0 Y_A<5 Y_A>0 Y_C<5 Y_C>0
接下来,我们尝试固定 X A = 2 , Y A = 2 X_A = 2, Y_A = 2 XA=2,YA=2,以 X C , Y C X_C, Y_C XC,YC为坐标轴,绘制相速矢量场,
plot(x, set_covar = list(X_A = 2, Y_A = 2))
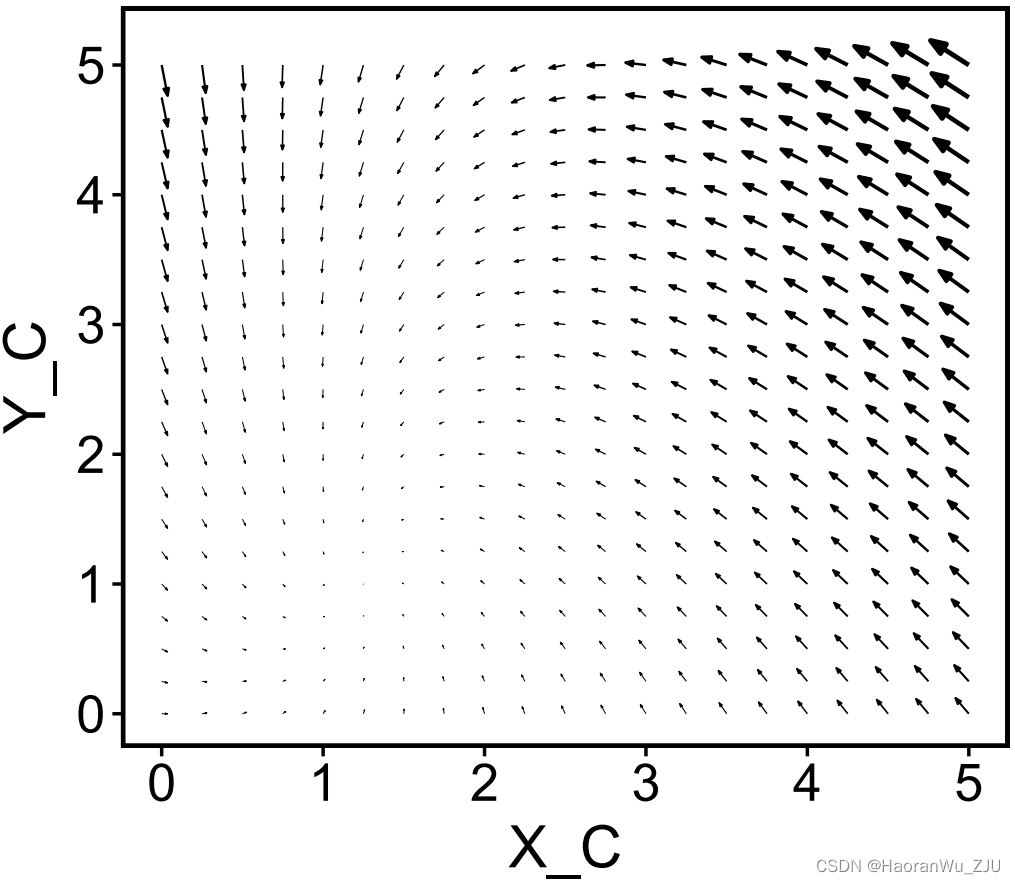
可以看到,该常微分方程组似乎在 X C , Y C X_C, Y_C XC,YC的值很小时存在使 d X C / d t , d Y C / d t = 0 dX_C/dt, dY_C/dt=0 dXC/dt,dYC/dt=0的点。
四、一维相速矢量场
如果一个常微分方程只有一个模型变量,或者在含有 n n n个模型变量的常微分方程组中,有 ( n − 1 ) (n-1) (n−1)个变量的值都被固定了,那么plot函数就会绘制一维的相速矢量场。
现在我们尝试固定 X A = 2 , Y A = 2 , X C = 2 X_A = 2, Y_A = 2, X_C = 2 XA=2,YA=2,XC=2。这样,只剩下模型变量 X A X_A XA的值没有被固定。plot函数将以 X A X_A XA为唯一的坐标轴,绘制一维的相速矢量场,
plot(x, set_covar = list(X_A = 2, Y_A = 2, X_C = 2))
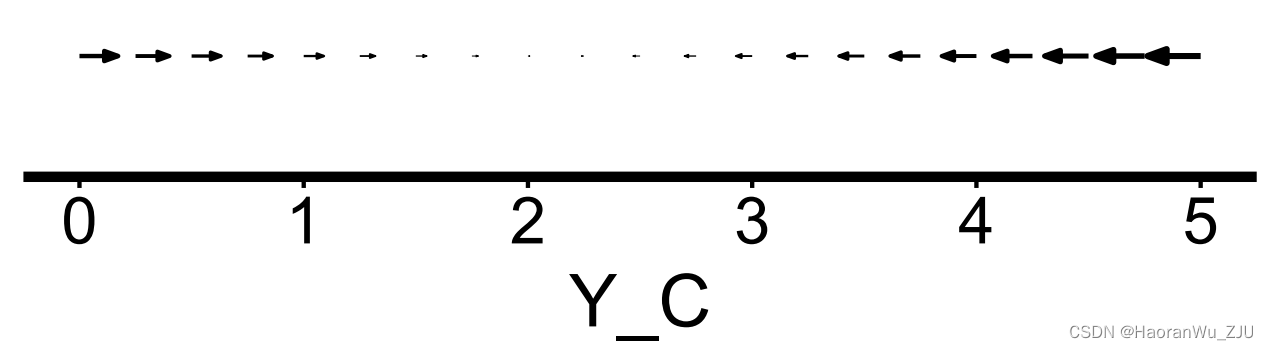
其中,每个相速矢量的值代表的是 d Y C / d t dY_C/dt dYC/dt在某一相点的对应值。
五、相速矢量
当所有模型变量都被赋值时,plot函数将会作出某一相点所对应的相速矢量。在相空间中,相速矢量的起点在其对应的相点,长度代表相点在相点在该处运动的速率。例如,在本节案例中,位于相点 ( X C 0 , Y C 0 , X A 0 , Y A 0 ) (X_{C0},Y_{C0},X_{A0},Y_{A0}) (XC0,YC0,XA0,YA0)的相速矢量的值为,
( d X C / d t , d Y A / d t , d X A / d t , d Y A / d t ) ∣ X C = X C 0 , Y C = Y C 0 , X A = X A 0 , Y A = Y A 0 (dX_C/dt,dY_A/dt,dX_A/dt,dY_A/dt)|_{X_{C}=X_{C0}, Y_{C}=Y_{C0}, X_{A}=X_{A0}, Y_{A}=Y_{A0}} (dXC/dt,dYA/dt,dXA/dt,dYA/dt)∣XC=XC0,YC=YC0,XA=XA0,YA=YA0
调用plot时,plot函数会画出相速矢量在各个维度上的值,
plot(x, set_covar = list(X_A = 2, Y_A = 2, X_C = 2, Y_C = 2))
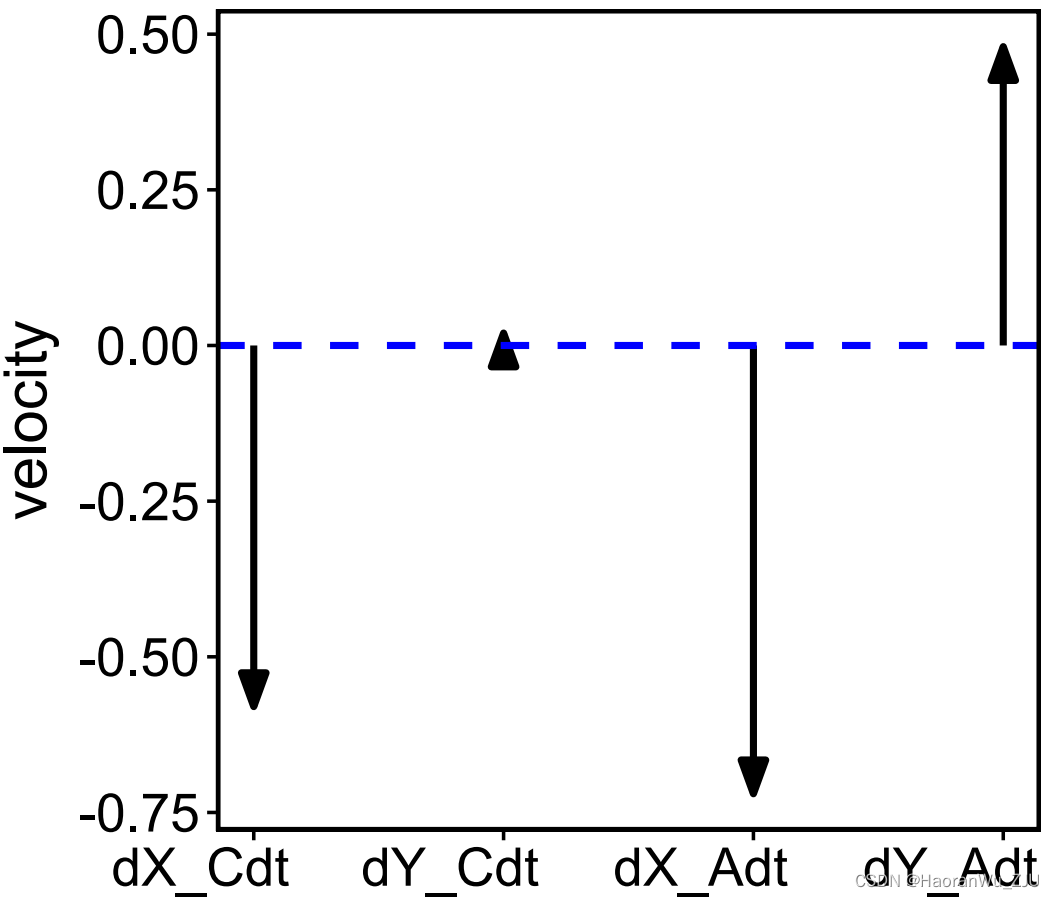
该图给出了相点 ( 2 , 2 , 2 , 2 ) (2,2,2,2) (2,2,2,2)所对应的相速矢量,其中横坐标的每一个标签代表相速矢量在某一维度上的分解值,即 d X C / d t ∣ X C = 2 , d Y C / d t ∣ Y C = 2 , d X A / d t ∣ X A = 2 , d Y A / d t ∣ Y A = 2 dX_C/dt|_{X_C=2}, dY_C/dt|_{Y_C=2}, dX_A/dt|_{X_A=2}, dY_A/dt|_{Y_A=2} dXC/dt∣XC=2,dYC/dt∣YC=2,dXA/dt∣XA=2,dYA/dt∣YA=2。
如何引用
Wu, H. (2023). ecode: An R package to investigate community dynamics in ordinary differential equation systems. bioRxiv, 2023-06.
原文见bioRxiv。
相关文章:

常微分方程建模R包ecode(二)——绘制相速矢量场
本节中我们考虑一个更为复杂的常微分方程模型, d X C d t ν ( X A Y A ) − β ⋅ X C ⋅ ( Y C Y A ) − ( μ g ) ⋅ X C , ( 1 ) d Y C d t β ⋅ X C ⋅ ( Y C Y A ) − ( μ g ρ ) ⋅ Y C , ( 2 ) d X A d t g ⋅ X C − β ⋅ X A ⋅ ( Y C Y A …...
学习C#编写上位机的基础知识和入门步骤:
00001. 掌握C#编程语言基础和.NET框架的使用。 00002. 学习WinForm窗体应用程序开发技术,包括控件的使用和事件驱动编程。 00003. 熟悉基本的数据结构和算法知识,如链表、栈、队列等。 00004. 理解串口通信协议和通信方法,用于与底层硬件设…...
简单高效!低代码搭建销售自动化程序的方法与实践
在当今数字化时代,销售自动化成为了提高销售效率和业绩的重要手段之一。而低代码平台的兴起,使得搭建销售自动化程序变得更加简单和高效。本文将介绍低代码平台及其优势,并探讨如何利用低代码平台搭建销售自动化程序。 1、低代码平台 1&…...

第九十三回 在Flutter中mock数据
文章目录 概念介绍使用方法示例代码 我们在上一章回中介绍了"在Flutter中解析JSON数据"相关的内容,本章回中将介绍 如何mock数据.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在本章回中介绍的mock数据主要是通过相关的代码模拟服务器…...

进程与线程的区别与联系
多进程已经可以很好的实现并发编程的效果了,但是仍然有一个明显的缺点:进程太重了,进程消耗的资源更多,速度更慢。如果进程创建销毁不频繁,那么还好,一旦需要大规模创建和销毁进程,开销就比较大…...

使用gadl对土地利用栅格重分类
要使用Python语言进行土地利用栅格的重分类,可以使用gadl库(GDAL的Python绑定)来实现。gadl库提供了一组功能强大的函数和类,可用于读取、处理和分析栅格数据。 首先,确保已经安装了gadl库。可以使用以下命令通过pip进…...
SQL-每日一题【1141. 查询近30天活跃用户数】
题目 活动记录表:Activity 请写SQL查询出截至 2019-07-27(包含2019-07-27),近 30 天的每日活跃用户数(当天只要有一条活动记录,即为活跃用户)。 以 任意顺序 返回结果表。 查询结果示例如下。…...
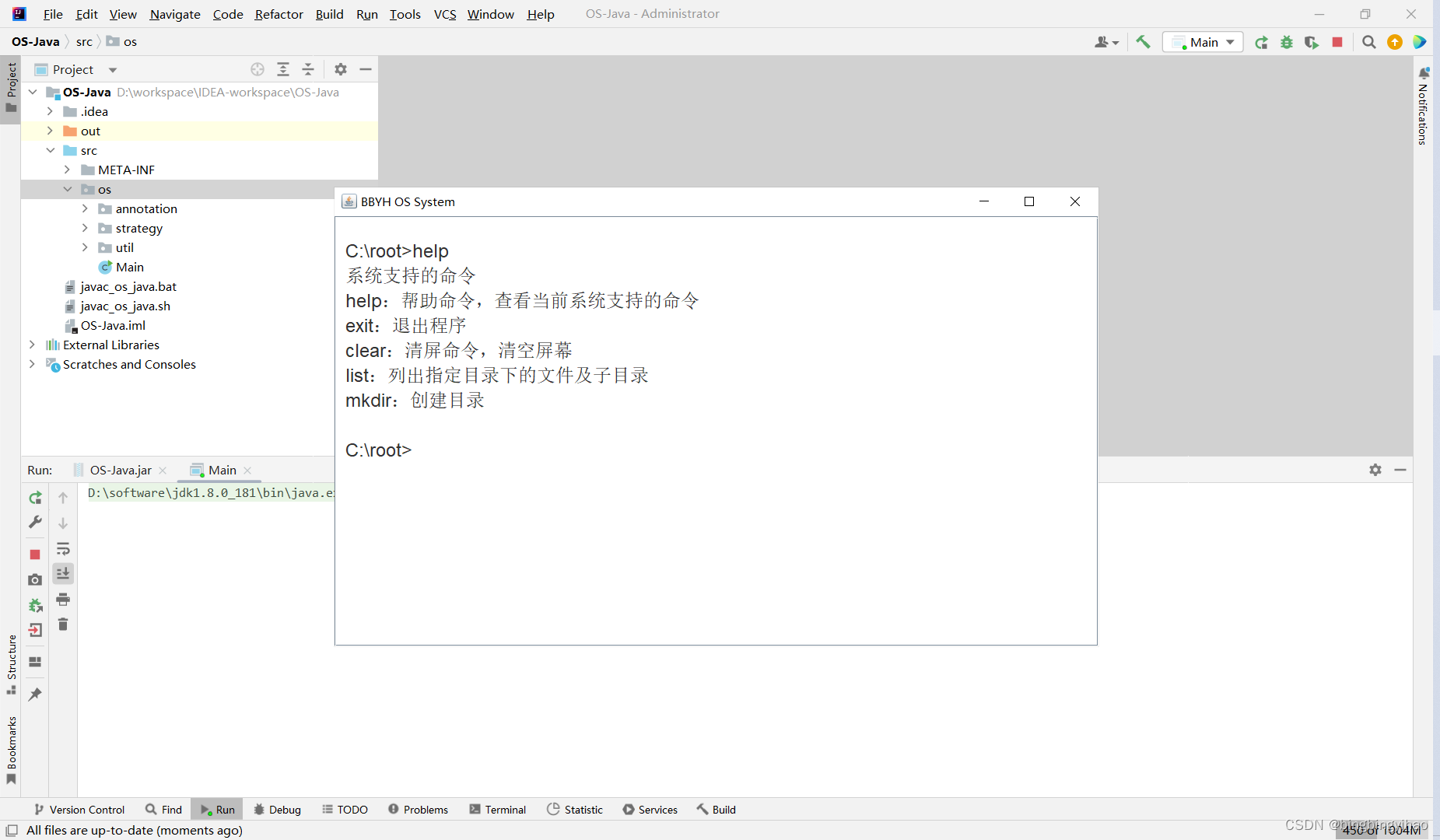
Java小型操作系统模拟(采用策略模式结合反射进行搭建,支持一些简单的命令)
Java小型操作系统模拟 项目说明第一阶段:反射结合策略模式搭建基本的命令结构第二阶段:注解结合反射与策略模式,将结构进一步规范第三阶段:开启新的窗口,将控制台输入切换到新窗口中,同时创建右键菜单&…...
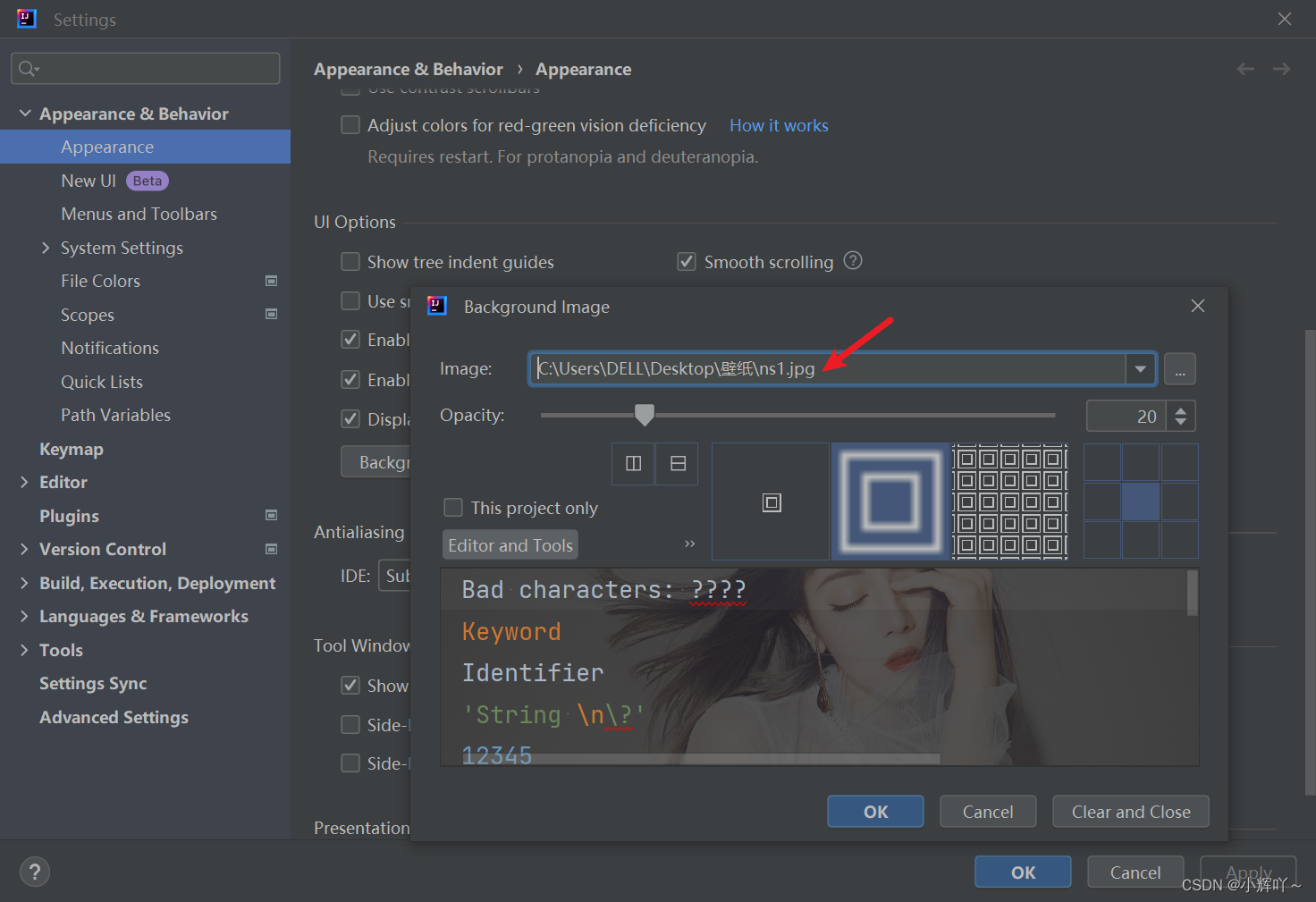
VsCode与Idea编辑器更换背景图
目录 VsCode Idea VsCode 需要安装background插件 安装完成后,打开设置,搜索background 然后就可以在json文件进行图片设置,透明度等等 Idea 打开File -> Settings 然后找到Appearance , 往下滑,找到BackGround …...

Visual Studio 快捷键
记录一下VS的快捷键,用Xcode几个星期后回到VS一下子有点乱,还好有条件反射在,过了会就都恢复了 目录 跳转快捷键查找快捷键编辑快捷键代码折叠书签操作记忆来源VS一定要装VAssistX插件,下面的快捷键部分是VX提供的。 跳转快捷键 快速打开文件 Alt + Shift + O 快速打开对…...

IT技术面试中常见的问题及解答技巧
在IT技术面试中,面试官常常会问到一些常见的问题,针对这些问题,我们可以充分准备和提前准备一些解答技巧。下面我将分享一些我个人的经验和观察,希望对大家有所帮助。 请介绍一下你的项目经验。 在回答这个问题时,我们…...

Java使用hive连接kyuubi
一、Maven依赖 <dependency><groupId>org.apache.hive</groupId><artifactId>hive-jdbc</artifactId><version>2.3.9</version> </dependency> 二、相关配置信息 驱动类:org.apache.hive.jdbc.HiveDriver连接UR…...

性能测试基础知识(三)性能指标
性能测试基础知识(三)性能指标 前言一、时间特性1、响应时间2、并发数3、吞吐量(TPS) 二、资源特性1、CPU利用率2、内存利用率3、I/O利用率4、网络带宽使用率5、网络传输速率(MB/s) 三、实例场景 前言 性能…...

【 Redis】的乱码问题
问题描述: 使用RedisTemplate存储的数据,在 redis-cli 客户端查看时,key 和 value 都会携带类似\xac\xad\这样的字符串。 原因: 由于默认使用了 jdk 的序列化方式。以下是支持的序列化方式 项目一般都会有缓存,常常…...
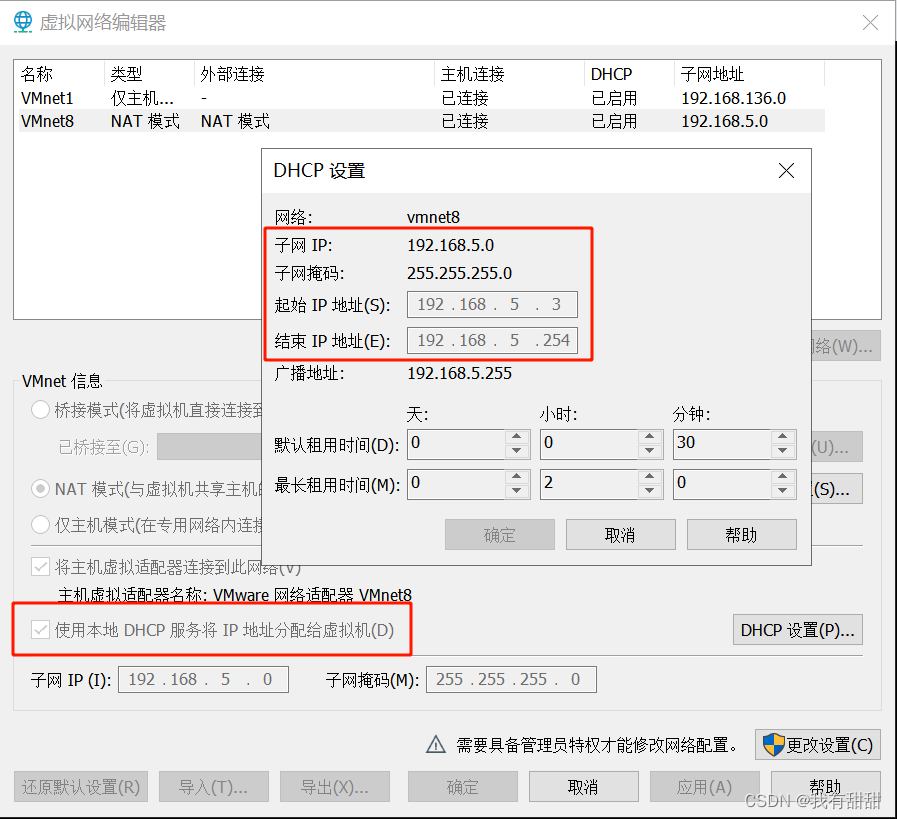
虚拟机安装的问题
CentOS7报错: Host SMBus Controller not enabled! 1.在上图界面中直接输入root用户的密码登录到系统 2.输入命令,lsmod | grep i2c 3.输入命令,vi /etc/modprobe.d/blacklist.conf 创建黑名单,添加以下内容: blacklist i2c_piix…...
seldom之数据驱动
seldom之数据驱动 如果自动化某个功能,测试数据不一样而操作步骤是一样的,那么就可以使用参数化来节省测试代码。 seldom是我在维护一个Web UI自动化测试框,这里跟大家分享seldom参数化的实现。 GitHub:GitHub - SeldomQA/seld…...
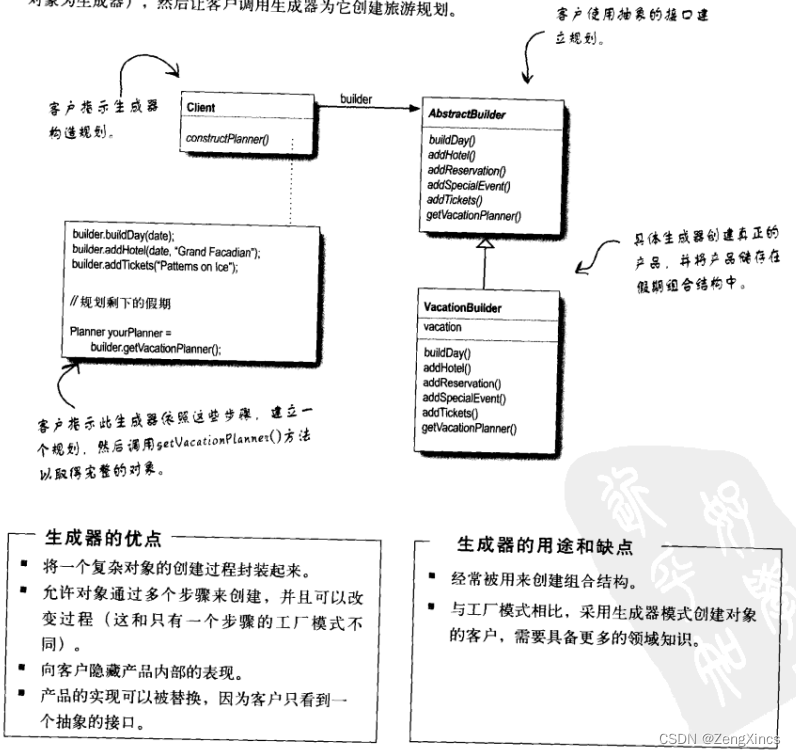
设计模式:生成器模式
这个模式书上讲的比较简单,但是感觉精华应该是讲到了。 引用下其它博客的总结:生成器模式的核心在于分离构建算法和具体的构造实现,从而使得构建算法可以重用。 【设计模式】建造者模式_鼠晓的博客-CSDN博客...
Gradle同步任务一直不动问题(非网络情况)
最近更新ComposeViews的Kotlin和Compose版本,升级到Kotlin1.9和Compose1.4.3时遇见一个问题,Gradle同步时始终会卡在一个位置,同步了一晚上也没用 然后又试了两次还是不行,猜测可能是Gradle的问题,于是使用命令行进行同步,并打印debug日志 ./gradlew -debug -refresh-dependen…...
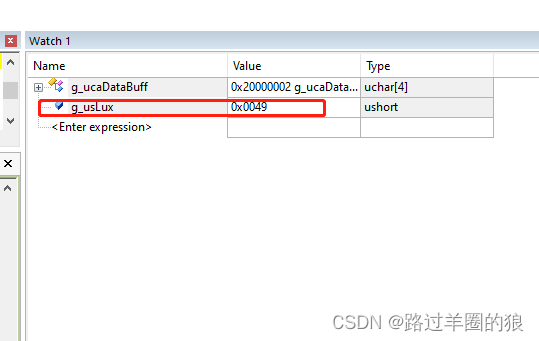
STM32使用HAL库BH1750光照度传感器
开发环境 单片机:STM32F103C8T6 光照度传感器:BH1750 IDE:KEILSTM32CUBEMX 单片机配置 1、STM32CUBEMX BH1750代码 1、头文件 /* ************************************************* BH1750光照数据计算(LUX) …...

qt代码练习
计时器练习 namespace Ui { class third; }class third : public QWidget {Q_OBJECTpublic:explicit third(QWidget *parent nullptr);~third();QLabel *labth1 new QLabel(this);QTextEdit *txtth1 new QTextEdit("闹钟",this);QLineEdit *leth1 new QLineEdit(t…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
