主成分分析
主成分分析
- 相关概念
- 方差
- 协方差
- 协方差矩阵
- 特征值和特征向量
- 主成分分析
- 数据降维
- 主成分分析原理
- 主成分分析过程
- sklearn库中的PCA
- 主成分分析实现案例
相关概念
方差
方差是一个用来衡量一组数据离散程度的统计量,它是各样本与样本均值的差的平方和的平均值。方差越大,表示数据的离散程度越大。
方差公式:
s 2 = ∑ i = 1 n ( x i − x ) 2 ) n − 1 s^2 = \frac{\sum_{i=1}^{n}(x_i - x)^2)}{n - 1} s2=n−1∑i=1n(xi−x)2)
协方差
协方差是一个用来衡量两个随机变量之间相关性或线性关系的统计量,它描述了两个随机变量的变化趋势是否一致。协方差的值可以为正、负或零,分别表示正相关、负相关或无相关。绝对值越大,表示两个随机变量的相关性越强。
然而,协方差的值无法直接比较,因为它受到随机变量尺度的影响。为了消除尺度影响,可以使用相关系数来衡量两个随机变量的相关性。
协方差公式:
c o v ( X , Y ) = ∑ i = 1 n ( X i − X ˉ ) ( Y i − Y ˉ ) n − 1 cov(X, Y) = \frac{\sum_{i=1}^{n}(X_i - \bar{X})(Y_i - \bar{Y})}{n - 1} cov(X,Y)=n−1∑i=1n(Xi−Xˉ)(Yi−Yˉ)
协方差矩阵
协方差矩阵是一个对称矩阵,用来衡量多个随机变量之间的相关性或线性关系。它描述了多个随机变量之间的变化趋势是否一致。
协方差矩阵可以用来衡量多个随机变量之间的相关性,可以通过观察矩阵中的元素值来判断变量之间的关系。对角线上的元素表示每个随机变量的方差,非对角线上的元素表示不同随机变量之间的协方差。
特征值和特征向量
在线性代数中,特征值和特征向量是矩阵的重要概念。
特征值(eigenvalue)是一个标量,表示线性变换中的一个重要性质。对于一个n×n的方阵A,如果存在一个非零向量v使得满足以下条件:
A v = λ v Av = λv Av=λv
其中,v是一个非零向量,λ是一个标量,则λ被称为矩阵A的特征值,v被称为对应于特征值λ的特征向量。
特征向量(eigenvector)是与特征值相关联的向量。特征向量是指在线性变换中,只发生伸缩而不改变方向的向量。特征向量可以通过特征值方程来求解。
特征值和特征向量的重要性在于它们提供了矩阵的重要性质和结构信息。通过求解特征值和特征向量,可以得到矩阵的主要特征、主要方向以及变换的性质。在数据分析和机器学习中,特征值和特征向量经常被用于数据降维、特征提取和数据压缩等任务。
主成分分析
数据降维
数据降维是指通过保留数据中最重要的信息,将高维数据转换为低维表示的过程。在实际应用中,高维数据可能存在冗余、噪声或者维度灾难等问题,这时候可以使用数据降维技术来减少数据的维度,从而简化数据分析和处理的复杂性。数据降维可以帮助我们在处理和分析大规模高维数据时更加高效和准确,同时可以减少存储空间和计算成本。
数据降维的主要目的是在尽量保留原始数据的关键特征的前提下,减少数据的维度。常见的数据降维方法包括主成分分析(PCA)、因子分析(FA)、独立成分分析(ICA)、线性判别分析(LDA)、奇异值分解(SVD)等。
主成分分析原理
主成分分析(Principal Component Analysis,PCA)是一种常用的无监督学习方法,主要用于数据降维和特征提取。其目的是通过线性变换将原始数据投影到一组新的正交特征上,使得投影后的数据具有最大的方差。这样可以保留最重要的信息,并且去除冗余的维度。换句话说,PCA试图找到最能够解释数据变异性的主要方向(主成分),这些主成分是数据中最重要的特征,通过按照方差大小递减的顺序选择,可以实现降维。
主成分分析可以把具有相关性的高维变量转换为线性无关的低维变量,称为主成分。主成分能够尽可能保留原始数据的信息。
矩阵的主成分就是其协方差矩阵对应的特征向量,按照对应的特征值大小进行排序,最大的特征值就是第一主成分,其次是第二主成分,依次类推。
主成分分析过程
主成分分析的步骤如下:
- 对数据进行标准化,使得每个特征的均值为0,方差为1。
- 计算协方差矩阵,反映不同特征之间的相关性。
- 对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。
- 将特征值按照大小排序,选择前k个特征值对应的特征向量作为主成分。
- 将原始数据与选取的主成分相乘,得到降维后的数据。
sklearn库中的PCA
sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)
- n_components – PCA算法中所要保留的主成分个数n,即保留下来的特征个数n;
int或string类型,缺省时默认为None,即所有成分被保留;
赋值为int,比如n_components=1,则将把原始数据降到一个维度;
赋值为string,比如n_components=‘mle’,则将自动选取特征个数n,使得满足所要求的方差百分比。 - copy – bool类型,True或者False,缺省时默认为True;
该参数表示是否在运行算法时,将原始训练数据复制一份。若为True,则运行PCA算法后,原始训练数据的值不会有任何改变,因为是在原始数据的副本上进行的运算;若为False,则运行PCA算法后,原始训练数据的值会发生改变,因为是在原始数据上进行的降维计算。 - whiten – bool类型,缺省时默认为False;
白化,使得每个特征具有相同的方差。如果为True,它会将分量向量标准化为单位方差,这在某些情况下可用于预测模型(默认为False)。
PCA对象的方法:
- fit(X, y=None)
fit()可以说是scikit-learn中通用的方法,每个需要训练的算法都会有fit()方法,它其实就是算法中的“训练”这一步骤。因为PCA是无监督学习算法,此处y自然等于None;
fit(X),表示用数据X来训练PCA模型;
pca.fit(X),表示用X对pca这个对象进行训练。 - fit_transform(X)
用X来训练PCA模型,同时返回降维后的数据;
newX=pca.fit_transform(X),newX就是降维后的数据。 - transform(X)
将数据X转换成降维后的数据。当模型训练好后,对于新输入的数据,都可以用transform()方法来降维。
主成分分析实现案例
已知鸢尾花数据是四维的,共三类样本。要求使用PCA算法对鸢尾花数据进行降维,并实现二维平面上的可视化。
代码实现:
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA # 导入PCA模块
from sklearn.datasets import load_iris # 导入鸢尾花数据集模块# 加载数据
data = load_iris() # 以字典形式加载鸢尾花数据集
X = data.data # 使用X表示数据集中的属性数据
y = data.target # 使用y表示数据集中的标签# 使用PCA算法进行数据降维
pca = PCA(n_components=2) # 创建PCA对象,设置降维后主成分个数为2
reduced_X = pca.fit_transform(X) # 对原始数据进行降维,降维后数据保存在reduced_X中# 按类别对降维后的数据进行保存
red_x, red_y = [], [] # 第一类数据点
green_x, green_y = [], [] # 第二类数据点
blue_x, blue_y = [], [] # 第三类数据点for i in range(len(reduced_X)): # 按照鸢尾花的类别将降维后的数据点保存在不同的列表中if y[i] == 0:red_x.append(reduced_X[i][0])red_y.append(reduced_X[i][1])elif y[i] == 1:green_x.append(reduced_X[i][0])green_y.append(reduced_X[i][1])else:blue_x.append(reduced_X[i][0])blue_y.append(reduced_X[i][1])# 降维后数据点的可视化
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(green_x, green_y, c='g', marker='D')
plt.scatter(blue_x, blue_y, c='b', marker='.')plt.show()
更详细的代码实现:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target# 数据标准化
# PCA算法对数据的尺度敏感,因此在应用PCA之前,需要对数据进行标准化处理,使得每个特征的均值为0,方差为1
X = (X - np.mean(X, axis=0)) / np.std(X, axis=0) # 标准化公式:(样本数据 - 样本均值) / 样本标准差# 计算协方差矩阵
cov_matrix = np.cov(X.T)# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)# 选择主成分
explained_variance_ratio = eigenvalues / np.sum(eigenvalues)# 降维
n_components = 2 # 选择降维后的维数
top_eigenvectors = eigenvectors[:, :n_components]
X_pca = X.dot(top_eigenvectors)# 按类别对降维后的数据进行保存
red_x, red_y = [], [] # 第一类数据点
green_x, green_y = [], [] # 第二类数据点
blue_x, blue_y = [], [] # 第三类数据点for i in range(len(X_pca)): # 按照鸢尾花的类别将降维后的数据点保存在不同的列表中if y[i] == 0:red_x.append(X_pca[i][0])red_y.append(X_pca[i][1])elif y[i] == 1:green_x.append(X_pca[i][0])green_y.append(X_pca[i][1])else:blue_x.append(X_pca[i][0])blue_y.append(X_pca[i][1])# 降维后数据点的可视化
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(green_x, green_y, c='g', marker='D')
plt.scatter(blue_x, blue_y, c='b', marker='.')plt.show()
相关文章:

主成分分析
主成分分析 相关概念方差协方差协方差矩阵特征值和特征向量 主成分分析数据降维主成分分析原理主成分分析过程sklearn库中的PCA主成分分析实现案例 相关概念 方差 方差是一个用来衡量一组数据离散程度的统计量,它是各样本与样本均值的差的平方和的平均值。方差越大…...
)
笙默考试管理系统-MyExamTest(26)
笙默考试管理系统-MyExamTest(26) 目录 一、 笙默考试管理系统-MyExamTest 二、 笙默考试管理系统-MyExamTest 三、 笙默考试管理系统-MyExamTest 四、 笙默考试管理系统-MyExamTest 五、 笙默考试管理系统-MyExamTest 笙默考试管理系统-MyEx…...
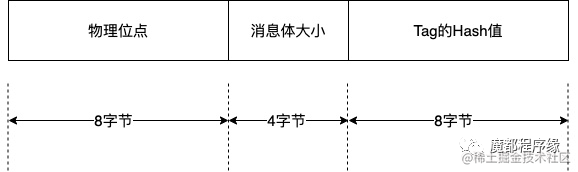
重新理解 RocketMQ Commit Log 存储协议
最近突然感觉:很多软件、硬件在设计上是有 root reason 的,不是 by desgin 如此,而是解决了那时、那个场景的那个需求。一旦了解后,就会感觉在和设计者对话,了解他们的思路,学习他们的方法,思维…...
ES6基础知识十:你是怎么理解ES6中 Decorator 的?使用场景?
一、介绍 Decorator,即装饰器,从名字上很容易让我们联想到装饰者模式 简单来讲,装饰者模式就是一种在不改变原类和使用继承的情况下,动态地扩展对象功能的设计理论。 ES6中Decorator功能亦如此,其本质也不是什么高大…...
接口/Web自动化测试如何做?框架如何搭建封装?
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 自动化测试怎么做…...

Linux怎么从网络上下载文件
wget命令用于从网络上下载文件 下载文件: wget [URL]使用wget命令加上要下载的文件的URL,可以将文件下载到当前目录。 指定保存的文件名: wget -O [保存的文件名] [URL]使用-O选项后跟保存的文件名,可以指定下载的文件保存的名称…...

Flutter携带JSON参数post请求
在Flutter中发送带有JSON参数的网络请求,你可以使用HTTP库(如http或dio)来实现。以下是使用http库发送网络请求并携带JSON参数的示例: import package:http/http.dart as http; import dart:convert;// 创建参数Map Map<Strin…...
【vue】vue-image-lazy图片懒加载使用与介绍【超详细+npm包源代码】
简介 当前插件是基于vue3,写的一个图片懒加载,文章最下方是npm包的源码,你可以自己拿去研究和修改,如有更好的想法可以留言,如果对你有帮助,可以点赞收藏和关注,谢谢。 后续会添加图片放大和切…...
MFC第二十四天 使用GDI对象画笔和画刷来开发控件(分页控件选择态的算法分析、使用CToolTipCtrl开发动静态提示)
文章目录 GDI对象画笔和画刷来开发控件梯形边框的按钮控件CMainDlg.hCMainDlg.cppCLadderCtrl.hCLadderCtrl.cpp 矩形边框的三态按钮控件 CToolTipCtrl开发动静态提示CMainDlg.hCMainDlg.cppCLadderCtrl.hCLadderCtrl.cpp: 实现文件 矩形边框的三态按钮控件 CToolTipCtrl开发动…...

【NLP-新工具】语音转文本与OpenAI的用途
一、说明 OpenAI最近2022发布了一个名为Whisper的新语音识别模型。与DALLE-2和GPT-3不同,Whisper是一个免费的开源模型。它的主要功能就是将语音翻译成文本。本文将介绍如何使用这个重要应用库。 二、 Whisper概念 2.1 Whisper是啥? Whisper 是一种自动…...

try-catch-finally的字节码原理
Java 中有一个非常重要的内容是 try-catch-finally 的执行顺序和返回值问题,其中 finally 一定会执行,但是为什么会这样? 下面看下 try-catch-finally 背后的实现原理 try-catch public class Test {public static void main(String[] args)…...
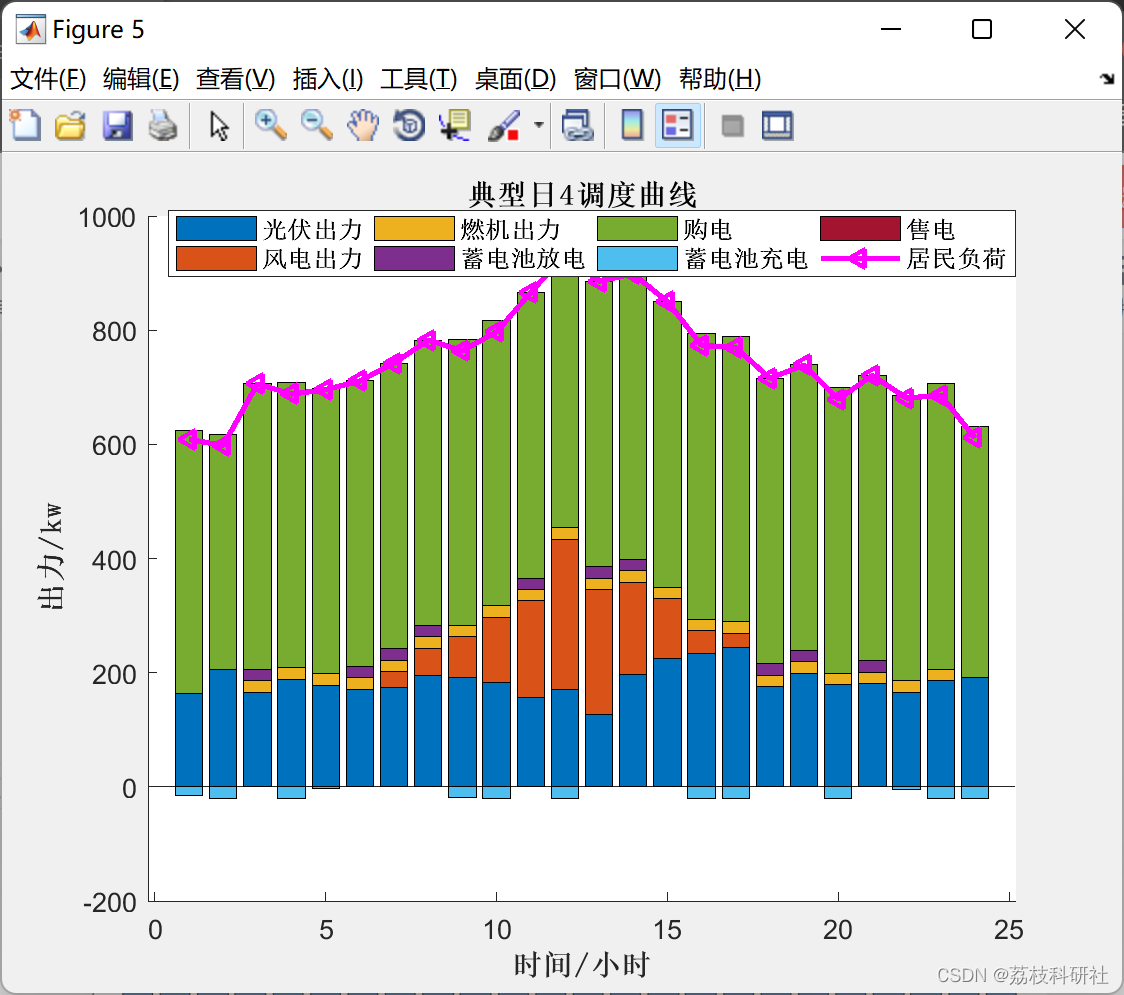
基于双层优化的微电网系统规划设计方法(Matlab代码实现)
目录 💥1 概述 1.1 微电网系统结构 1.2 微电网系统双层规划设计结构 1.3 双层优化模型 1.4 上层容量优化模型 1.5 下层调度优化模型 📚2 运行结果 🎉3 文献来源 🌈4 Matlab代码、数据、文章讲解 💥1 概述 文献来源&…...
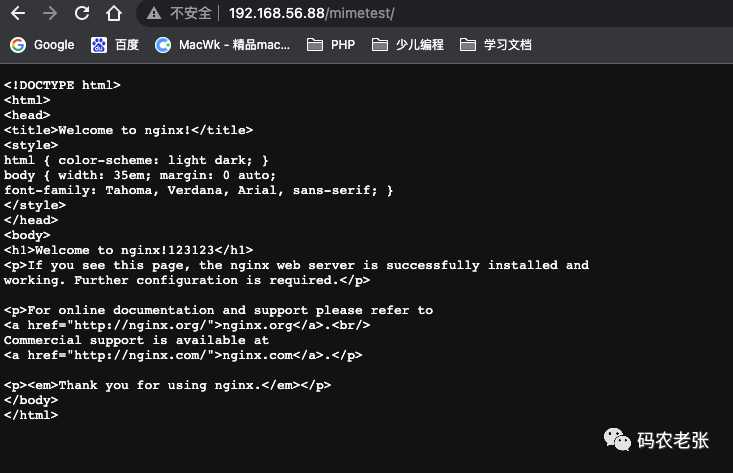
【Nginx13】Nginx学习:HTTP核心模块(十)Types、AIO及其它配置
Nginx学习:HTTP核心模块(十)Types、AIO及其它配置 今天学习的内容也比较简单,主要的是 Types 相关的配置,另外还会了解一下 AIO 以及部分没有特别大的分类归属的配置指令的使用。后面的内容都是 HTTP 核心模块中比较小…...

2023年华数杯数学建模C题思路分析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 组织机构4 建模常见问题类型4.1 分类问题4.2 优化问题4.3 预测问题4.4 评价问题 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor 1 竞赛信息 为了培养学生的创新意识及运用数…...
安卓手机变身Linux服务器
文章目录 前言一、准备工作1、安卓手机2、下载软件二、开始安装1、检查系统,确认版本并安装2、配置(安卓7.0 及以上的用户忽略此步)3、问题处理【没有异常的小伙伴忽略】总结前言 在实际开发中有很多地方都需要服务器资源,但是服务器资源不论在哪里都是比较紧缺的资源,今…...

【Ansible】Ansible自动化运维工具之playbook剧本
playbook 一、playbook 的概述1. playbook 的概念2. playbook 的构成 二、playbook 的应用1. 安装 httpd 并启动2. 定义、引用变量3. 指定远程主机 sudo 切换用户4. when条件判断5. 迭代6. Templates 模块6.1 添加模板文件6.2 修改主机清单文件6.3 编写 playbook 7. tags 模块 …...

Yolov8目标检测
Yolov8目标检测 目录 Yolov8目标检测一、准备数据集二、源码下载配置2.1 下载库2.2 修改配置2.3 训练2.4 验证2.5 测试2.6 模型导出2.7 本地测试 一、准备数据集 Yolov8只支持yolo格式的数据,所以,需要将数据集格式调整为 datasets|images|train|00000…...

Jmeter用于接口测试中,关联如何实现
Jmeter用于接口测试时,后一个接口经常需要用到前一次接口返回的结果,应该如何获取前一次请求的结果值,应用于后一个接口呢,拿一个登录的例子来说明如何获取。 1、打开jmeter, 使用的3.3的版本,新建一个测试计划&#x…...

线程状态
从卖包子的案例学习进程间的通信 public class Test {public static void main(String[] args) {Object objnew Object();Thread th1new Thread(){Overridepublic void run() {synchronized (obj){System.out.println("来三个包子!");try {obj.wait(); /…...
HTML一些基础知识
1、Web标准:主要包含结构、表现、行为。结构用于对网页元素进行整理和分类,主要指HTML。表现用于设置网页元素的板式、颜色、大小等外观样式,主要指的是CSS。行为主要指的是网页模型的定义以及交互的编写,主要是js文件。 Html相当…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
