7-16 验证“哥德巴赫猜想” (20 分)
7-16 验证“哥德巴赫猜想” (20 分)
数学领域著名的“哥德巴赫猜想”的大致意思是:任何一个大于2的偶数总能表示为两个素数之和。比如:24=5+19,其中5和19都是素数。本实验的任务是设计一个程序,验证20亿以内的偶数都可以分解成两个素数之和。
输入格式:
输入在一行中给出一个(2, 2 000 000 000]范围内的偶数N。
输出格式:
在一行中按照格式“N = p + q”输出N的素数分解,其中p ≤ q均为素数。又因为这样的分解不唯一(例如24还可以分解为7+17),要求必须输出所有解中p最小的解。
输入样例:
24
输出样例:
24 = 5 + 19
代码如下:
#include<stdio.h>
#include<math.h>
int prime(int n)
{int i,flag=1;if(n<2) return 0;else {for(i=2;i<=sqrt(n);i++){if(n%i= =0){flag=0;break;}}}if(flag==1) return 1;else return 0;
}
int main()
{int n,i,j,k=0;scanf("%d",&n);for(i=2;i<n;i++){if(prime(i)){if(prime(n-i)){printf("%d = %d + %d",n,i,n-i);goto loop;}}}loop:return 0;
}
相关文章:
)
7-16 验证“哥德巴赫猜想” (20 分)
7-16 验证“哥德巴赫猜想” (20 分) 数学领域著名的“哥德巴赫猜想”的大致意思是:任何一个大于2的偶数总能表示为两个素数之和。比如:24519,其中5和19都是素数。本实验的任务是设计一个程序,验证20亿以内的偶数都可以…...
GEE学习02 --设置Jupyter Notebook的打开路径
直接双击Jupyter Notebook 桌面图标运行时,打开的文件路径是默认的:C:\用户\用户名 如果使用python命令提示符打开jupyter notebook , 而我新建的GEE学习文件夹在另一个路径,可以直接修改默认的保存路径:…...
stm32与上位机电脑间最快的通信方式是什么?
对于小型多关节机械臂的控制电路设计,选择合适的通信方式可以提高MCU与上位机之间的实时性。以下是一些在STM32上常用的通信方式,你可以根据你的具体需求选择适合的: 串口通信(UART):串口通信是一种常见的…...

pytorch学习——卷积神经网络——以LeNet为例
目录 一.什么是卷积? 二.卷积神经网络的组成 三.卷积网络基本元素介绍 3.1卷积 3.2填充和步幅 3.2.1填充(Padding) 填充是指在输入数据周围添加额外的边界值(通常是零),以扩展输入的尺寸。填充可以在卷…...
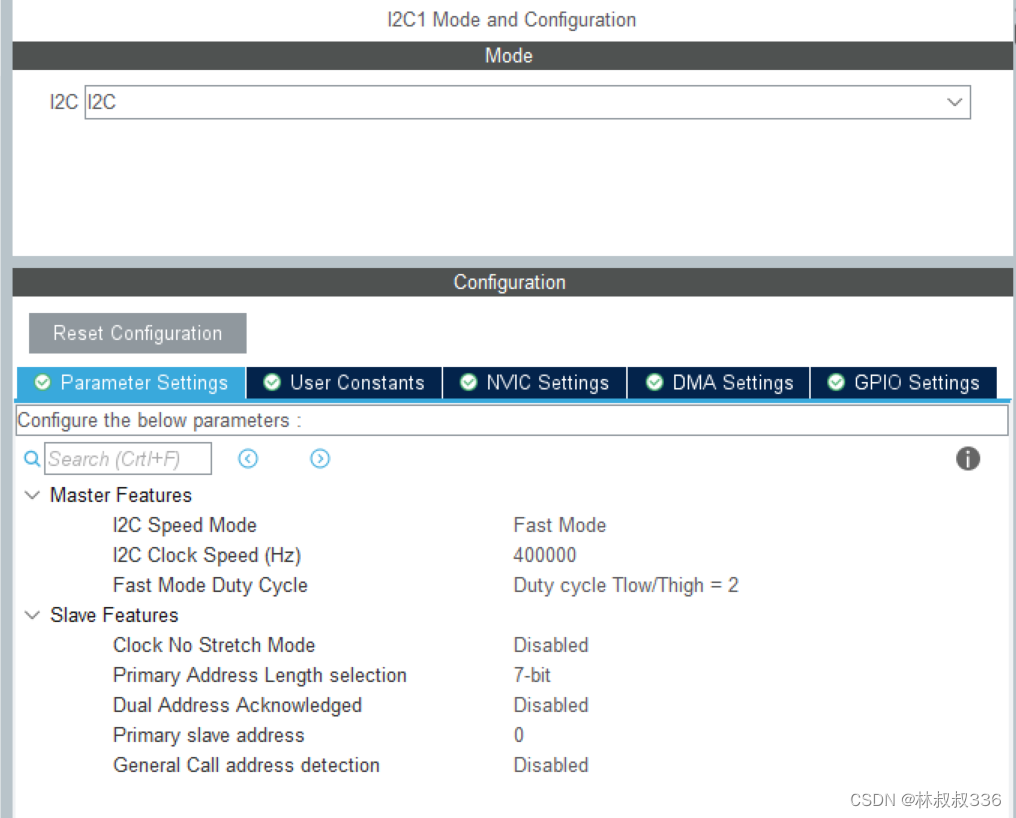
stm32 mpu6050 cubemx DMP法读取角度
文章目录 前言一、相关文件二、cubemx配置三、代码变量初始化主循环 总结 前言 文件 记录使用dmp库来读取mpu6050的角度。 这是参考文件 参考1–主要参考 github参考 参考2 参考三 一、相关文件 相关文件在这里下载(未填,不过可以在上面的git中下载&a…...

.Net6 Core Web API 配置 log4net + MySQL
目录 一、导入NuGet 包 二、添加配置文件 log4net.config 三、创建MySQL表格 四、Program全局配置 五、帮助类编写 六、效果展示 小编没有使用依赖注入的方式。 一、导入NuGet 包 ---- log4net 基础包 ---- Microsoft.Extensions.Logging.Log4Net…...

校园跑腿小程序运营攻略
作为一名校园跑腿小程序的运营者,你可能会面临诸如用户获取、平台推广、服务质量保证等挑战。在本篇推文中,我将为你提供一些关键的运营策略,帮助你成功运营校园跑腿小程序。 1. 用户获取和留存 用户是校园跑腿小程序成功的关键。以下是一些…...
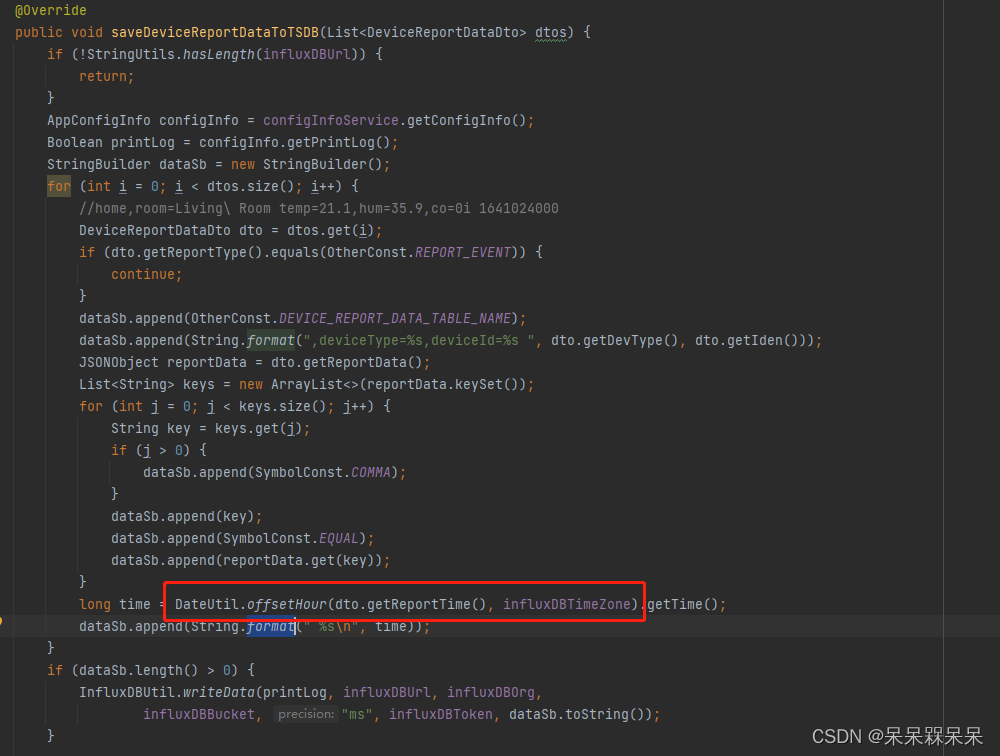
InfluxDB2如何求增量数据
需求 项目中需要接入电表设备,求用电量。 按天和设备统计用电量 按天统计用电量 统计总用电量 存在的问题 difference 函数可以求增量,但是以上计算均存在一个问题,比如xx设备有8.1号和8.2号的数据,我统计每天的用电量…...
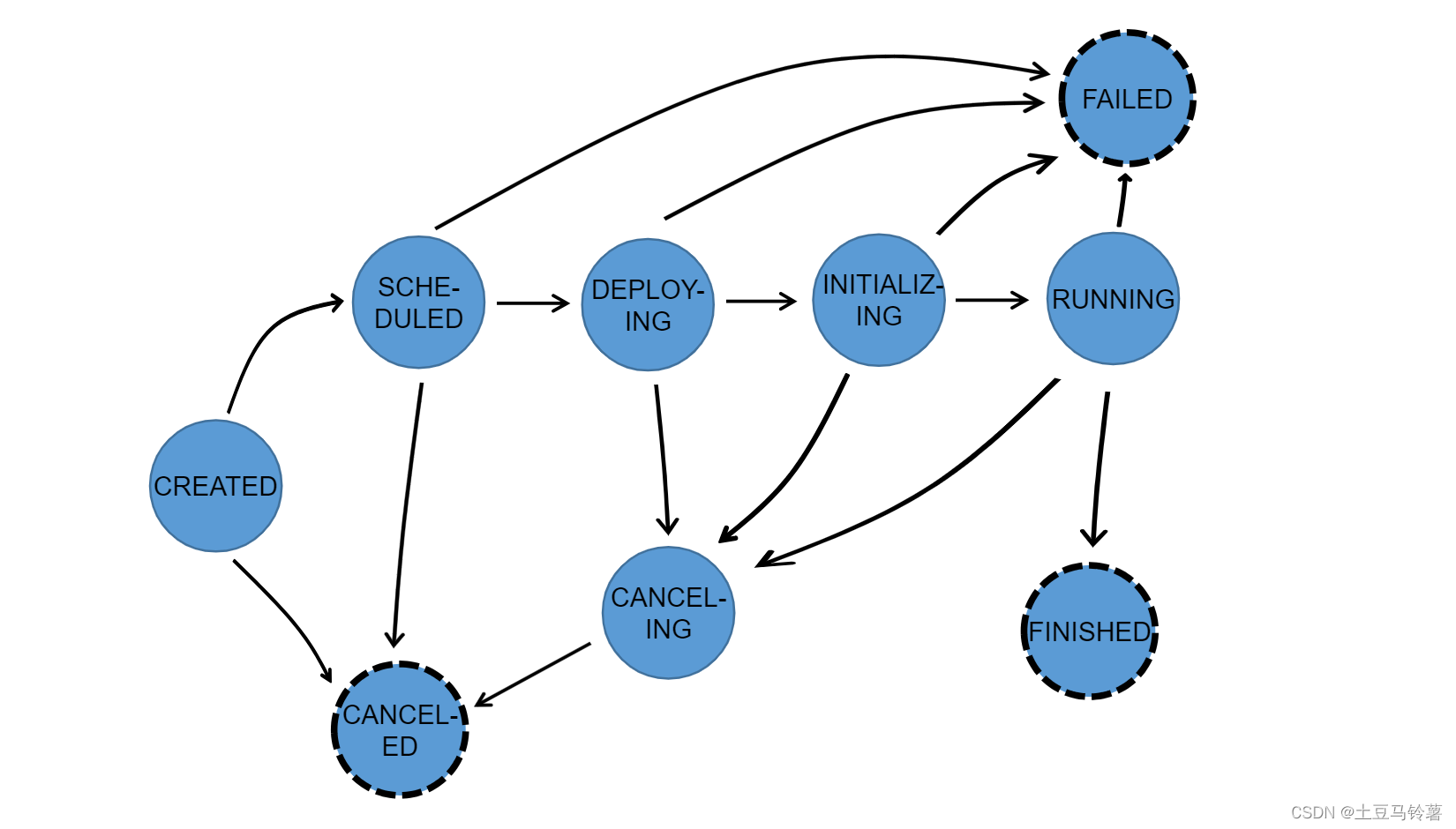
Flink作业调度的9种状态
1.什么是作业调度 Flink 通过 Task Slots 来定义执行资源。每个 TaskManager 有一到多个 task slot,每个 task slot 可以运行一条由多个并行 task 组成的流水线。 这样一条流水线由多个连续的 task 组成,比如并行度为 n 的 MapFunction 和 并行度为 n 的…...

8、Kubernetes核心技术 - ConfigMap
目录 一、ConfigMap概述 二、ConfigMap创建 2.1、命令行方式创建 2.2、yaml 文件方式创建 三、ConfigMap查询 四、ConfigMap更新 4.1、kubectl edit方式 4.2、kubectl apply方式 五、ConfigMap使用 5.1、spec.env 【环境变量】 5.2、spec.envFrom 【环境变量】 5.3…...
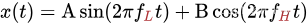
音视频--DTMF信号发送及检测
参考资料 https://zh.wikipedia.org/wiki/%E5%8F%8C%E9%9F%B3%E5%A4%9A%E9%A2%91https://www.cnblogs.com/lijingcheng/p/4454932.html 1. DTMF是什么 1.1 DTMF定义 双音多频信号(英语:Dual-Tone Multi-Frequency,简称:DTMF&a…...
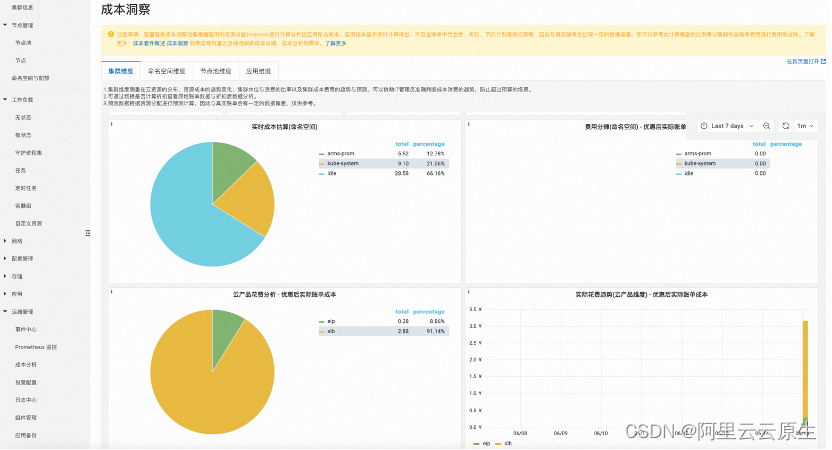
阿里云容器服务助力极氪荣获 FinOps 先锋实践者
作者:海迩 可信云评估是中国信息通信研究院下属的云计算服务和软件的专业评估体系,自 2013 年起历经十年发展,可信云服务评估体系已日臻成熟,成为政府支撑、行业规范、用户选型的重要参考。 2022 年 5 月国务院国资委制定印发《…...

C++ 通过time.windows.com获取时间
C++ 通过time.windows.com获取时间 在C++中,你可以使用 <ctime>头文件中的 time()函数来获取当前的系统时间。然后,你可以使用 <ctime>头文件中的 localtime()函数将时间转换为本地时间,并从中获取小时、分钟和秒。 以下是一个示例代码,演示如何通过time.windo…...
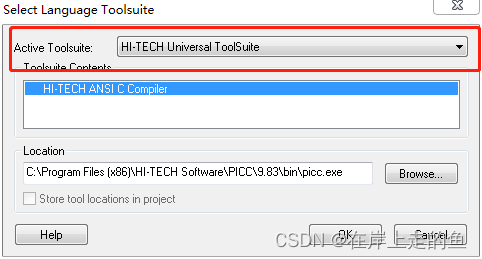
MPLAB加载c文件为什么不能添加到工程中的source files中
MPLAB加载c文件为什么不能添加到工程中的source files中 因为你安装好MAPLAB软件之后你的编译器是默认的编译器,所以当你添加C文件时,软件是不认识C文件的,只有手动的将编译器改成自安装的PICC编译器才能进行C文件的正确加载。 具体修改步骤…...

Tcp的粘包和半包问题及解决方案
目录 粘包: 半包: 应用进程如何解读字节流?如何解决粘包和半包问题? ①:固定长度 ②:分隔符 ③:固定长度字段存储内容的长度信息 粘包: 一次接收到多个消息,粘包 应…...

路由的hash和history模式的区别
目录 ✅ 路由模式概述 一. 路由的hash和history模式的区别 1. hash模式 2. history模式 3. 两种模式对比 二. 如何获取页面的hash变化 ✅ 路由模式概述 单页应用是在移动互联时代诞生的,它的目标是不刷新整体页面,通过地址栏中的变化来决定内容区…...
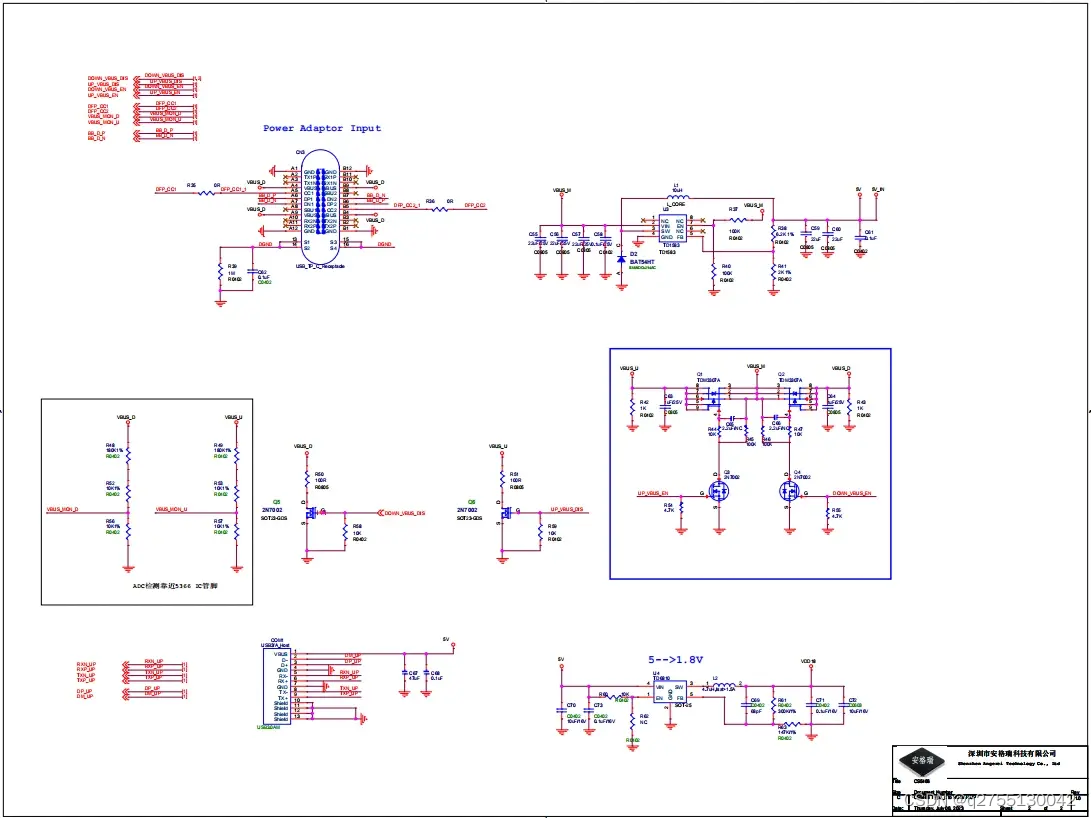
CS5366+VL171母座正反插HDMI(CS5466也可搭配)国产芯片TYPEC方案设计 ASL电路原理图 集睿致远+威锋设计
VL171是威锋芯片,可搭配ASL集睿致远CS5366设计TypeC母座正反插转HDMI高清投屏方案,CS5366是2lane 芯片,支持4K60HZ,是CS5266的升级版,CS5366设计拓展坞方案可以替代CS5266携带快充100W的PD和US,多口HUB也不在话下,而画面的刷新率和…...

mxgraph的核心元素详谈
前言: MxGraph是一个流行的开源图形库,它提供了一stop solution for creating graphical representations of data。下面是MxGraph的核心源码讲解: 正文: Graph Structure(图结构): MxGraph将一个图表示为一个层次结构,由节点和边组成。节点表示图中的顶点,而边表示它…...

再探C++——默认成员函数
目录 一、构造函数 二、析构函数 三、赋值运算符 四、拷贝构造 如果一个类中没有成员,我们称为空类。空类,也存在6个默认的类成员函数。 默认成员函数:用户不显示地写,编译器会默认生成的函数叫做默认成员函数。 6个默认成员…...
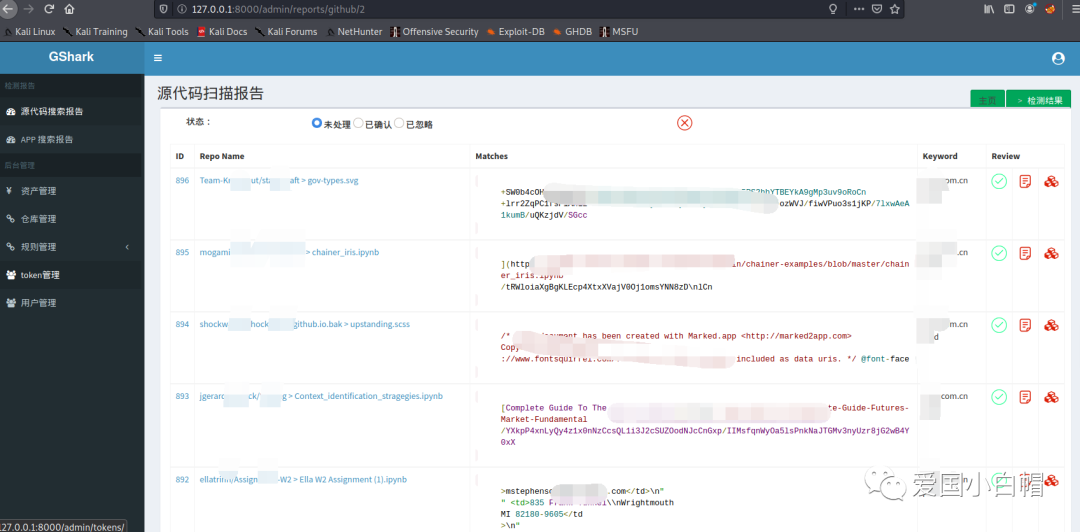
推荐两款github敏感信息搜集工具(gsil、gshark)
推荐两款github敏感信息搜集工具(gsil、gshark) - 云社区 - 腾讯云 (tencent.com) github敏感信息泄露是很多企业时常忽视的一个问题,国外有一份研究报告显示,在超过24,000份的GitHub公开数据中,发现有数千个文件中可能…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...

机器学习复习3--模型评估
误差与过拟合 我们将学习器对样本的实际预测结果与样本的真实值之间的差异称为:误差(error)。 误差定义: ①在训练集上的误差称为训练误差(training error)或经验误差(empirical error&#x…...
