刷题记录:牛客NC19429红球进黑洞 区间拆位异或+区间求和
传送门:牛客
题目描述:
区间求和+区间异或k
输入:
10 10
8 5 8 9 3 9 8 3 3 6
2 1 4 1
1 2 6
2 9 10 8
1 1 7
2 4 7 8
2 8 8 6
2 2 3 0
1 1 2
2 9 10 4
1 2 3
输出:
33
50
13
13
一道区间求和+区间异或的题目,可以称得上是线段树的一道好题
首先对于异或运算来说,并不满足区间分配率,也就是说对于(a+b)(a+b)(a+b)^c≠c\neqc= aaa^c + bbb^c,那么对于此时的区间异或来说,我们似乎没有了求出对和的贡献的方法.
我们需要换一种思路去思考这道题.对于异或来说,一般关于异或的题目总是在二进制数上面出题目的.我们想一下对于一个区间的每一个数字来说,我们将原本的十进制加法变成二进制加法是不是也是可以的.那么对于二进制加法来说,我们需要知道什么?显然我们需要知道每一位区间内所有数字在这一位是111的个数.只要我们知道每一位1的个数,那么我们进行加法也就不难了.
因此我们此时可以使用线段树来存储每一个区间中的每一位的1的个数和0的个数.(根据数据范围来看,我们此时存储32位即可).这样想的话这道题就变得很明了了,我们记录了一个区间中每一位的0和1的个数,那么对于我们的区间异或k来说,我们只要知道k的二进制位中哪一个数字是1哪一个数字是0即可.因为对于异或来说,0不改变,1会使原数取反,那么对于有1的位置,那么就意味着那一个位置的0与1的个数调换一下即可.并且对于异或操作来说,我们满足结合律的性质,意味着我们可以用懒标记来记录我们的区间异或
具体细节可以参考代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define int long long
#define maxn 100100
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{int l,r,lazy,bit0[34],sum,bit1[34];
}tree[maxn*4];
int n,m;int a[maxn];
void pushup(Segment_tree &u,Segment_tree &l,Segment_tree &r) {u.sum=l.sum+r.sum;for(int i=0;i<=32;i++) {u.bit0[i]=l.bit0[i]+r.bit0[i];u.bit1[i]=l.bit1[i]+r.bit1[i];}
}
void pushup(int rt) {pushup(tree[rt],tree[ls],tree[rs]);
}
void build(int l,int r,int rt) {tree[rt].l=l;tree[rt].r=r;if(l==r) {tree[rt].sum=a[l];int v=a[l];int cnt=0;while(v) {if(v&1) tree[rt].bit1[cnt]=1;else tree[rt].bit0[cnt]=1;cnt++;v>>=1;}if(v==0) {//注意这里,我们必须要求出所有的32位,因为对于0的位置我们依旧需要记录该位置有0//当时就是这一步忽略了,导致我调试了几个小时!!while(cnt<=32) {tree[rt].bit0[cnt]=1;cnt++;}}return ;}int mid=(l+r)>>1;build(lson);build(rson);pushup(rt);
}
int get_num(int rt) {int SUM[34]={0};int jw=0;for(int i=0;i<=32;i++) {SUM[i]=(tree[rt].bit1[i]+jw)%2;jw=(tree[rt].bit1[i]+jw)/2;}int ans=0;int k=1;for(int i=0;i<=32;i++) {ans+=k*SUM[i];k*=2;}return ans;
}
void change(int rt,int v) {tree[rt].lazy^=v;for(int i=0;i<=32;i++) {if(v&1) {swap(tree[rt].bit1[i],tree[rt].bit0[i]);}v>>=1;if(v==0) break;}tree[rt].sum=get_num(rt);
}
void pushdown(int rt) {change(ls,tree[rt].lazy);change(rs,tree[rt].lazy);tree[rt].lazy=0;
}
void update(int l,int r,int v,int rt) {if(tree[rt].l==l&&tree[rt].r==r) {change(rt,v);return ;}if(tree[rt].lazy) pushdown(rt);int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid) update(l,r,v,ls);else if(l>mid) update(l,r,v,rs);else update(l,mid,v,ls),update(mid+1,r,v,rs);pushup(rt);
}
Segment_tree query(int l,int r,int rt) {if(tree[rt].l==l&&tree[rt].r==r) {return tree[rt];}if(tree[rt].lazy) pushdown(rt);int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid) return query(l,r,ls);else if(l>mid) return query(l,r,rs);else {auto Left=query(l,mid,ls);auto Right=query(mid+1,r,rs);Segment_tree Ans;pushup(Ans,Left,Right);return Ans;}
}
signed main() {n=read();m=read();for(int i=1;i<=n;i++) a[i]=read();build(root);for(int i=1;i<=m;i++) {int opt=read();if(opt==1) {int l=read(),r=read();printf("%lld\n",query(l,r,1).sum);}else {int l=read(),r=read(),k=read();update(l,r,k,1);}}return 0;
}
相关文章:

刷题记录:牛客NC19429红球进黑洞 区间拆位异或+区间求和
传送门:牛客 题目描述: 区间求和区间异或k 输入: 10 10 8 5 8 9 3 9 8 3 3 6 2 1 4 1 1 2 6 2 9 10 8 1 1 7 2 4 7 8 2 8 8 6 2 2 3 0 1 1 2 2 9 10 4 1 2 3 输出: 33 50 13 13一道区间求和区间异或的题目,可以称得上是线段树的一道好题 首先对于异或运算来说,并不满足…...

信息数智化招采系统源码——信息数智化招采系统
信息数智化招采系统 服务框架:Spring Cloud、Spring Boot2、Mybatis、OAuth2、Security 前端架构:VUE、Uniapp、Layui、Bootstrap、H5、CSS3 涉及技术:Eureka、Config、Zuul、OAuth2、Security、OSS、Turbine、Zipkin、Feign、Monit…...
20230217使AIO-3399J开发板上跑通Android11系统
20230217使AIO-3399J开发板上跑通Android11系统 2023/2/17 15:45 1、解压缩SDK:rk3399-android-11-r20211216.tar.xzrootrootrootroot-X99-Turbo:~$ tar xvf rk3399-android-11-r20211216.tar.xz 2、编译U-boot: rootrootrootroot-X99-Turbo:~/rk3399-a…...
Java 基础面试题——面向对象
目录1.面向对象和面向过程有什么区别?2.面向对象的有哪些特征?3.静态变量和实例变量有什么区别?4.Java 对象实例化顺序是怎样的?5.浅拷贝和深拷贝的区别是什么?5.1.浅拷贝5.2.深拷贝5.3.总结6.Java 中创建对象的方式有哪几种&…...
,依赖免费pdfbox)
PDF文件替换内容(电子签章),依赖免费pdfbox
首先提前准备,压入如下依赖 <!-- https://mvnrepository.com/artifact/org.apache.pdfbox/pdfbox --> <dependency> <groupId>org.apache.pdfbox</groupId> <artifactId>pdfbox</artifactId>…...
nvm 控制 node版本
nvm 官网 https://nvm.uihtm.com/ 1、卸掉nodejs,根据官网操作 2、如果之前安装过的nodejs,且安装的目录改变了,需重新配置系统环境 第一步:打开此电脑 > 右键属性 > 高级系统设置 > 环境变量 第二步: 在系统变量中选中…...

javaEE 初阶 — 传输层 TCP 协议中的异常情况与面向字节流的粘包问题
文章目录1 粘包问题1.1 什么是粘包问题1.2 如何解决粘包问题2 异常情况TCP 的十个特性:确认应答机制 超时重传机制 连接管理机制 滑动窗口 流量控制与拥塞控制 延迟应答与捎带应答 1 粘包问题 1.1 什么是粘包问题 面向字节流引入了一个比较麻烦的粘包问题。 …...

IP路由基础
——IP路由基础(IA)—— HCIA全套笔记已经上线(arpAAAvlanTrunk链路聚合vlan间通信ACL广域网技术以太网交换...........)_孤城286的博客-CSDN博客 目录 ——IP路由基础(IA)—— (1&#…...
12.centos7部署sonarqube9.6
12.centos7部署sonarqube9.6环境:sonarqube9.6Postgresql13JDK11sonarqube9.6下载地址:Postgresql13 rpm下载地址:JDK11下载地址:准备工作:修改文件句柄数(最大文件数)和用户最大进程数限制修改…...

大学四年自学Java编程,现在拿到28万年薪的offer,还是觉得挺值的
最近刚拿到美团的Java后端工程师的offer,(底薪、奖金、补贴、年终奖、五险一金)总包加在大概有28万的年薪,实际到手不会有这么多,但是我对于这个待遇还是非常满意的。说来还是非常的感慨,我属于那种从大一到…...

MySQL的日志详解
目录 一.介绍 日志分类 二.错误日志 三.二进制日志—binlog 概述 日志格式 操作 四.查询日志 五.慢查询日志 一.介绍 在任何一种数据库中,都会有各种各样的日志,记录着数据库工作的方方面面,以帮助数据库管理员追踪数据库曾经发生过的…...

输出该股票所有收盘比开盘上涨3%以上的日期
1:输出该股票所有收盘比开盘上涨3%以上的日期 #codingutf-8 import tushare as ts import pandas as pd import numpy as np#获取某支股票的历史行情数据 dfts.get_hist_data(code600519,start2001-01-01) #将互联网上的数据获取并且存储到本地 df.to_csv(./maotai…...
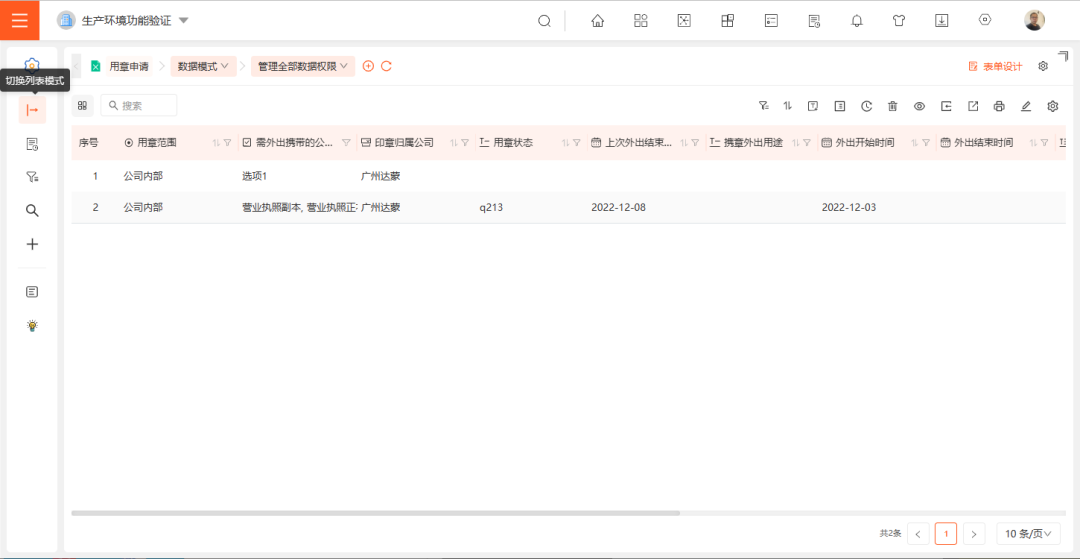
数值卡,让数据可视化玩出新花样丨三叠云
数值卡 路径 仪表盘 >> 仪表盘设计 功能简介 1. 数值卡增加「数值标题」、「图标」、「进度条」功能,使得应用场景更为广泛,实现数据可视化,让用户能够轻松地获取、处理信息。 2.「数据模型」支持0个维度1个指标、1个维度1个指标。…...

有这几个表现可能是认知障碍前兆
我国目前对于认知障碍的认知率、就诊率、诊断率很低,然而认知障碍如果能在早期发现,并及时治疗,生活质量会有效提高,缓解家属的精神和经济负担。所以,认知障碍的前兆一定要了解。1.记忆力减退,一周内的重要…...
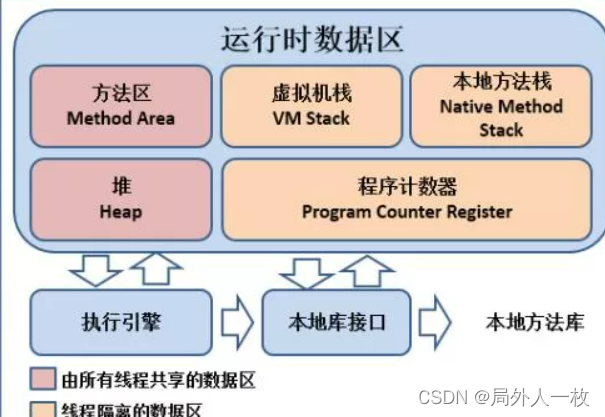
java面试题-阿里真题详解
前言 大家好,我是局外人一枚,最近有不少粉丝去阿里巴巴面试了,回来之后总结不少难题给我,以下是面试的真题,跟大家一起来讨论怎么回答。 阿里一面 1、说⼀下ArrayList和LinkedList区别 ⾸先,他们的底层数…...

JSON格式解析关键词搜索API
为了进行此平台API的调用,首先我们需要做下面几件事情。 1、 获取一个KEY。 2、 参考API文档里的接入方式和示例。 3、查看测试工具是否有需要的接口,响应实例的返回字段是否符合参数要求。 4、利用平台的文档中心和API测试工具,对接口进…...
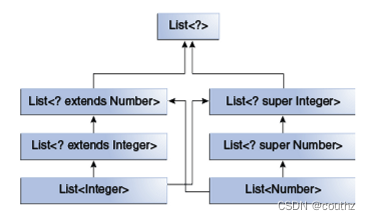
【Java基础】泛型(二)-泛型的难点:通配符
本文将尝试将通配符和泛型中的继承,多态一并讲解 关于泛型中继承的注意事项 因为Integer、Double继承了Number,根据多态性,以下语句是合法的 Number n new Integer(10); // OK, 父类引用变量可以指向子类对象 n 2.9 // OK,n实…...

黑马】后台管理-两个括号的坑
记录一下这两天的坑没想到后台管理系统上线这两天都没有搞明白1.首先第一个坑是使用node.js的express中间件框架创建一个微型服务器,然后将vue脚手架生成的dist文件夹的文件放入里面了 ,把项目加载到web服务器之后运行node .\app.js,页面显示…...

05:进阶篇 - 使用 CTKWidgets
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 CTKWidgets 包含了一组 Qt 部件,用于生物医学成像应用程序。当然,即使你的程序与医学无关,很多部件也是很有参考意义的。 在 CTK 源码中,有很多选项开关,可以控制你想要编译的内容(详见:04:进阶篇 …...
【YOLO V5】代码复现过程
接上篇,讲到如何从mask转成YOLOv5训练需要的txt数据集格式,这篇就在此基础上进行模型训练预测和部署转换吧! 目录 1.环境准备 2.YOLO训练 2.1 数据集准备 2.2 data.yaml准备 2.3 yolov5.yaml准备 2.4 训练命令 3.YOLO预测 3.1OLOv5 P…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
