概率和似然
在日常生活中,我们经常使用这些术语。但是在统计学和机器学习上下文中使用时,有一个本质的区别。本文将用理论和例子来解释概率和似然之间的关键区别。
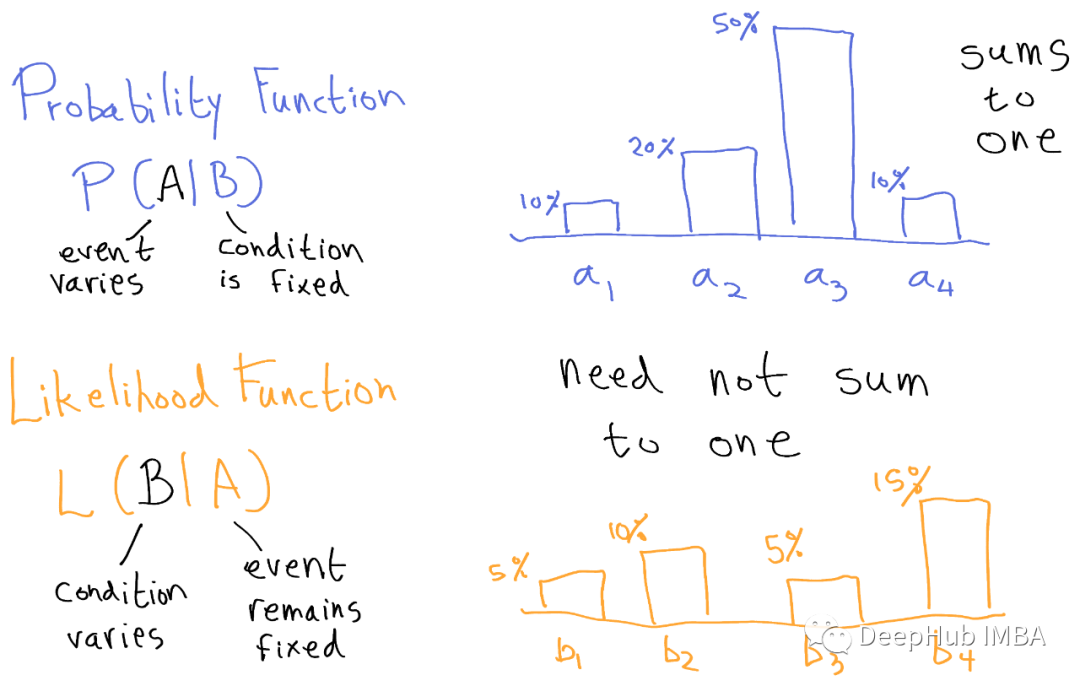
概率与似然
假设在一场棒球比赛中,两队的队长都被召集到场上掷硬币。获胜的队长将根据掷硬币的结果选择先击球还是先投球。
现在,获胜的队长选择先击球的概率是多少?我们现在知道只有两种可能的结果:获胜的队长决定先投球或开始击球。获胜的队有50%的几率会选择先击球。

评论员现在正在讨论获胜队长选择首先在击球的可能性。在实际中这个数字可能不到 50%,因为选择先击球会受球场类型、天气、对方球队等因素的影响。比如说如果比赛前下了大雨,决定先击球的可能性会低至 1%。如果天气条件恰到好处,那么获胜的队选择先击球的可能性可能高达 95%。
所以在计算概率值时,我们相信参数值θ=0.5是正确的。在考虑了所有参数之后,我们假设我们确定参数值 θ=0.5。但是在计算似然时,我们的目标是确定我们是否可以信任该参数。
所以我们可以说概率是基于纯数学的;然而似然是一个有许多参数和条件的函数。
为什么似然不是概率分布?
在抛硬币的情况下,我们可以阐述以下关于潜在结果 x 的情况。
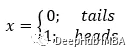
硬币正面朝上的概率是,
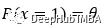
在此基础上,我们可以提出以下关于求硬币正面朝上和反面朝上的概率的问题。
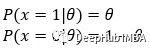
下面的方程可以推广前一组方程。
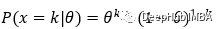
现在,我们可以看到上面的公式适用于k=1和k=0的值。

有了以上的基础,现在要考虑两种不同的情况。
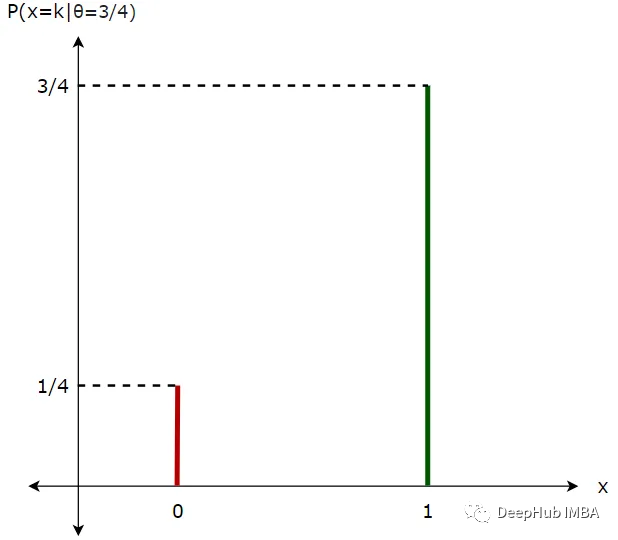
1、概率
假设在抛硬币之前,我们知道参数θ=3/4的值。在此基础上可以说得到正面的概率是P(正面)= θ = 3/4, P(反面)= 1-θ = 1/4。让我们把这些数据画在一个简单的图表上。我们保持参数(θ)不变,并改变数据(x=1或x=0)。
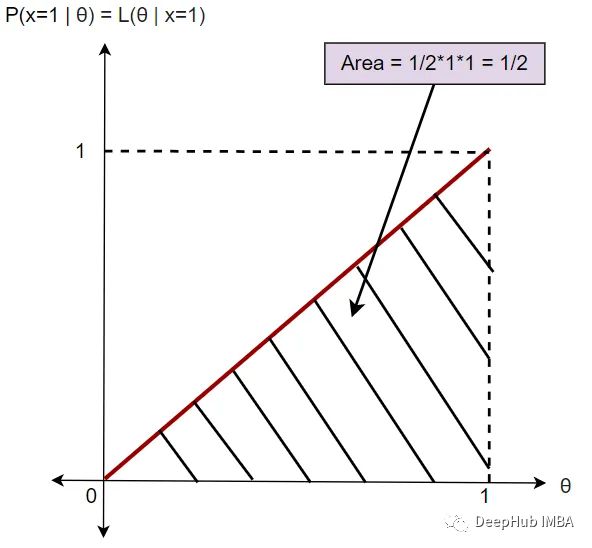
2、似然
现在,假设我们在抛硬币之前不知道正面或反面的概率,而我们有数据的结果, 也就是说我们已经掷过硬币。现在,给定 x=1,找到 θ 的概率是多少。在这种情况下,我们保持数据 (x=1) 不变并更改参数 (θ)。
我们目标是想找到定义这种结果的分布。简而言之,我们想要找到给定 x 的 θ 值。可以将其写成如下的数学格式。
P(x=1 | θ) = L(θ | x=1)
这里需要注意的关键是曲线下的面积是1/2。所以,我们可以说它不是一个有效的概率分布。它被称为似然分布。似然函数不服从概率定律。因此似然函数在[0,1]区间内是无界的。
概率和似然之间的关键区别
假设我们从参数化分布 F(X;θ) 中得到一个随机变量 X。在此参数化分布中,θ 是定义分布 F(X;θ) 的参数。随机变量 X=x 的概率为 P(X=x) = F(x;θ),这里的参数 θ 是已知的。
而我们一般情况下会拥有现实世界中的数据 (x),而定义分布 (θ) 的参数是未知的。给定模型 F(X;θ),似然度定义为观测数据 X 随 θ 变化的概率。我们可以将其写为 L(θ) = P(θ; X=x)。这里X 已知,但定义分布 (θ) 的参数未知。定义似然的动机是为了确定分布的参数。
在我们的日常生活中,经常将概率和似然称为同一事物。例如:明天下雨的概率是多少?或者明天下雨的可能性(似然)有多大?但是这些术语在机器学习和统计学中有很大不同。下面的一个例子可以解释概率和似然之间的关键区别。
当我们计算概率结果时,我们假设模型的参数是值得信赖的。但是当我们计算似然时,我们会根据我们观察到的样本数据来确定我们是否可以信任模型中的参数。
抛硬币
如果一枚硬币正面朝上和背面朝上的概率相等,就称其为均匀硬币。换句话说,P(正面)= P(反面)= 1/2。
假设有一枚均匀硬币。我们假设硬币参数值(θ = 0.5)。在寻找概率时,我们假设参数是可信的。也就是说如果我们抛这枚硬币一次,它正面朝上的概率是1/2。现在我们抛硬币100次,发现只有12次是正面朝上的。基于这些证据,我们会说硬币是均匀的可能性非常低。因为如果硬币是均匀的,我们预计它正面朝上的概率是一半,也就是50次。
在上面的例子中,我们可以说,100次硬币正面朝上的概率只有12次,这让我们高度怀疑,因为在给定的条件中,硬币正面朝下的实际概率实际上是p = 0.5。但如果这枚硬币55次正面,我们就可以说这枚硬币很可能是均匀的。
概率问题和统计问题的区别
假设我们还是抛硬币。考虑以下两个场景。
概率问题:
我们假设硬币是均匀的。连续得到两个正面的概率是多少?
它表示给定参数值(P = 0.5),观察数据(序列)的概率是多少。
统计问题:
我们不知道硬币是否公平(我们正在试图确定硬币的公平性)。假设我们抛硬币两次,连续得到两次正面。
问:根据观察到的数据,这枚硬币是均匀的可能性有多大?(p = 0.5)?
这意味着我们在给定数据(sequence = HH)的情况下确定参数的值(P = 0.5)。也就是说“我们的样本在多大程度上支持我们的假设 P = 0.5?”
我们可以将似然定义为参数模型中样本对给定参数值的支持程度的度量。
二项分布的概率和似然
继续抛硬币,让我们考虑一个简单的二项分布的例子。假设我们抛硬币十次,并记录结果。结果是9次正面1次反面。
我们知道硬币是均匀的,即p = 0.5。根据这个信息,我们要算出投掷10次得到9次正面的概率。我们可以用公式

这里0.009765是在p = 0.5的情况下得到x = 9个正面的概率。
一般情况下我们可以这样写:
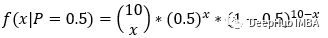
下面,如果我们不确定硬币是否均匀。这意味着我们不知道参数p的值。而我们已经投掷了十次硬币,并得到了投掷结果。结果是9次正面1次反面。基于此,我们可以得出以下结论。
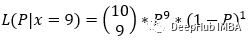
在这里,我们试图根据给定的数据样本(10次抛掷中有9次正面)找到参数P的值。
总结
在机器学习的背景下:
- 概率是指基于模型中参数指定的值,特定结果发生的概率,我们相信参数值是准确的。
- 似然指的是样本对参数模型中给定参数值的支持程度,我们试图根据提供的样本数据确定模型的参数值。
https://avoid.overfit.cn/post/02f9cd888b274752b17a9fc3f1120fbc
作者:Pratik Shukla
相关文章:
概率和似然
在日常生活中,我们经常使用这些术语。但是在统计学和机器学习上下文中使用时,有一个本质的区别。本文将用理论和例子来解释概率和似然之间的关键区别。 概率与似然 假设在一场棒球比赛中,两队的队长都被召集到场上掷硬币。获胜的队长将根据掷…...
前期软件项目评估偏差,如何有效处理?
1、重新评估制定延期计划 需要对项目进行重新评估,将新的评估方案提交项目干系人会议,开会协商一致后按照新的讨论结果制定计划,并实施执行。 软件项目评估偏差 怎么办:重新评估制定延期计划2、申请加资源 如果项目客户要求严格&a…...

Xline v0.2.0: 一个用于元数据管理的分布式KV存储
Xline是什么?我们为什么要做Xline? Xline是一个基于Curp协议的,用于管理元数据的分布式KV存储。现有的分布式KV存储大多采用Raft共识协议,需要两次RTT才能完成一次请求。当部署在单个数据中心时,节点之间的延迟较低&a…...

CompletableFuture
一、一个示例回顾Future 一些业务场景我们需要使用多线程异步执行任务,加快任务执行速度。JDK5新增了Future接口,用于描述一个异步计算的结果。虽然Future以及相关使用方法提供了异步执行任务的能力,但是对于结果的获取却是很不方便,我们必须使用Future.get()的方式阻塞调…...

面试不到10分钟就被赶出来了,问的实在是太变态了...
干了两年外包,本来想出来正儿八经找个互联网公司上班,没想到算法死在另一家厂子。 自从加入这家外包公司,每天都在加班,钱倒是给的不少,所以也就忍了。没想到11月一纸通知,所有人不许加班,薪资…...
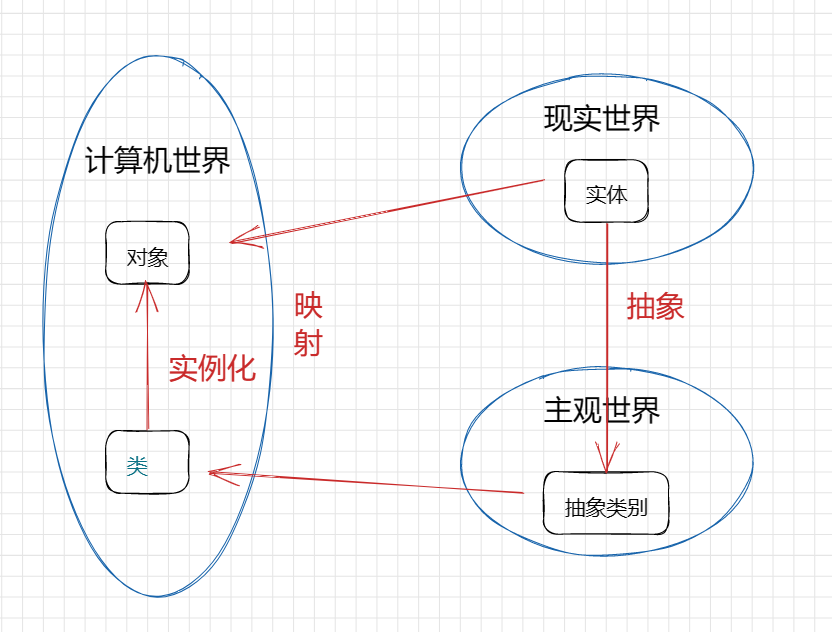
【C++】类与对象 (四)初始化列表 static成员 友元 内部类 匿名对象 拷贝对象时的一些编译器优化
前言 本章就是我们C中类与对象的终章了,不过本章的难度不大,都是类中一些边边角角的知识,记忆理解就行了,相信经过这么长时间的学习类与对象,你对面向对象也有了更加深的理解,最后我们学习完边边角角的一些…...

04:进阶篇 - 编译 CTK
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 在使用 CTK 之前,首先要进行编译。但要成功编译它,并不是一件很容易的事,这不仅取决于平台、Qt 的版本,也取决于编译器,以及所使用的 IDE。 平台(Linux、Windows)Qt 版本(4.x、5.x、6.x)编译器(MS…...

SQL73 返回所有价格在 3美元到 6美元之间的产品的名称和价格
描述有表Productsprod_idprod_nameprod_pricea0011egg3a0019sockets4b0019coffee15【问题】编写 SQL 语句,返回所有价格在 3美元到 6美元之间的产品的名称(prod_name)和价格(prod_price),使用 AND操作符&am…...

【Linux 多线程互斥】如何保证锁的原子性(互斥的原理)
临界资源:可以被多个执行流(线程或者叫轻量级进程)同是访问的(多个执行流共享的,比如:全局、堆等等);临界区:访问这些临界资源的代码;原子性:没有中间态&…...

Android 实现沉浸式全屏
前言 本文总结 Android 实现沉浸式全屏的实现方式。 实现沉浸式全屏 在一些需要全屏显示的场景下,比如玩游戏、看横屏视频的时候,内容全屏,占满窗口的体验会让用户更加沉浸到对内容的消费中,带来好的用户体验。 沉浸式显示具体来说就是如状态栏和导航栏部分的显示效果调…...

数据分析与SAS学习笔记6
数据集整理: 目的:对数据集中的数据进行预处理,使数据更适合统计分析过程对数据格式的要求; 常见整理要求: 1)建立新的变量,衍生变量,删除某些原变量; 2)…...
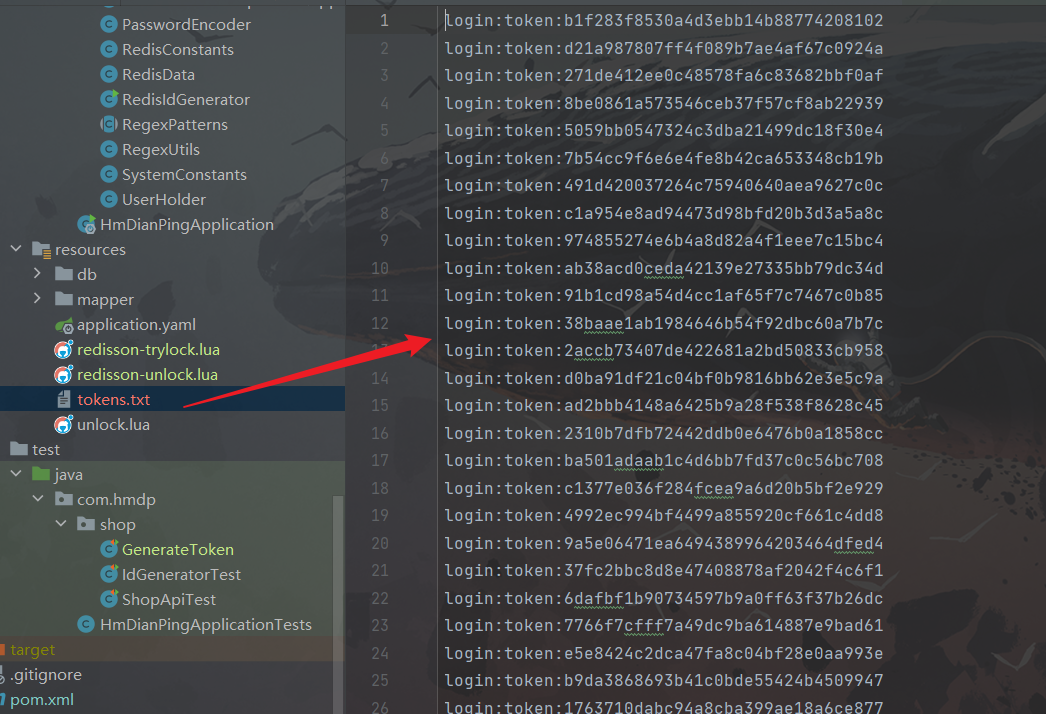
自动化完成1000个用户的登录并获取token并生成tokens.txt文件
自动化完成1000个用户的登录并获取token并生成tokens.txt文件 写作背景 在我学习使用redis实现秒杀功能的过程中,在编写完秒杀代码后,需要使用Jmeter实际测试1000个用户进行秒杀,由于秒杀功能需要在用户登录完成后才能实现,用户是…...

2023年全国最新安全员精选真题及答案1
百分百题库提供安全员考试试题、建筑安全员考试预测题、建筑安全员ABC考试真题、安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.(单选题)在起重作业中,()…...
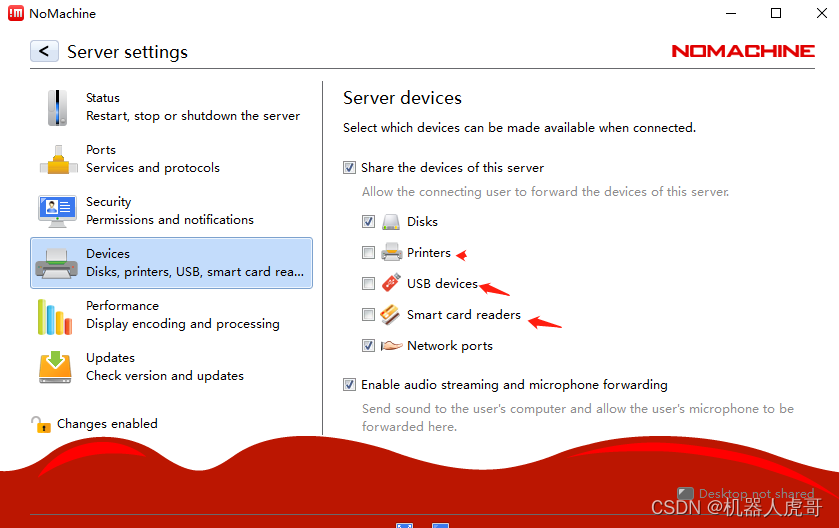
NoMachine 输入用户名密码后 闪断 解决办法
大家好,我是虎哥,最近工作忙,好长时间没有继续套件的深度学习,今天周六,难得有空,泡好茶,打开电脑,链接套件桌面,得,出问题了,一个很奇怪的问题&a…...

WebADI - 参数的使用
* 本文仅供交流分享,不作为专业指导 最近研究了一下WEBADI文档下载的参数,由于网上这块资料较少,所以专意分享下我的笔记。 准备 集成器:BHSC_EMP_ADI 表值集:BHSC_DEPT_LOV(值:dname&#x…...

【OJ】两个圆
📚Description: 直角坐标系内现有两个半径相等的圆,问两圆的位置关系。 位置关系有:重合,相切,相离,相交; 若两圆相交,需要求出两圆的重叠面积。 ⏳Input: 输入包含多组数据&a…...

一文读懂澳洲医疗:白菜价的药物怎么领?
众所周知,福利优厚的澳洲,在医疗系统上有着令全世界人民都羡慕的超高福利。 几十万的天价药,在澳洲,白菜价就能轻松到手。 国内70万元一针的“诺西那生钠注射液”(目前中国国内唯一治疗脊髓性肌萎缩症的进口精准靶向药…...

scrum看板视图切换时间线视图做项目管理
企业需要开发一个项目,可以制作时间线进行管理,以便参与者和管理者了解项目的时间进度。项目进行到哪一步,参与者有哪些,责任人是谁,这些都可以通过时间线进行展示。「时间线视图」是一种比甘特图更轻量、更实用的工具…...

10、MySQL查询优化
MySQL查询优化 1.MySQL查询优化技术2.子查询优化2.1 优化器自动优化2.2 优化措施:子查询合并2.2 优化措施:子查询上拉技术3.外连接消除4.生产环境不使用join联表查询5.group by分组优化5.1 group by执行流程5.2 为什么group by要创建临时表6.order by排序优化7.MySQL性能抖动…...
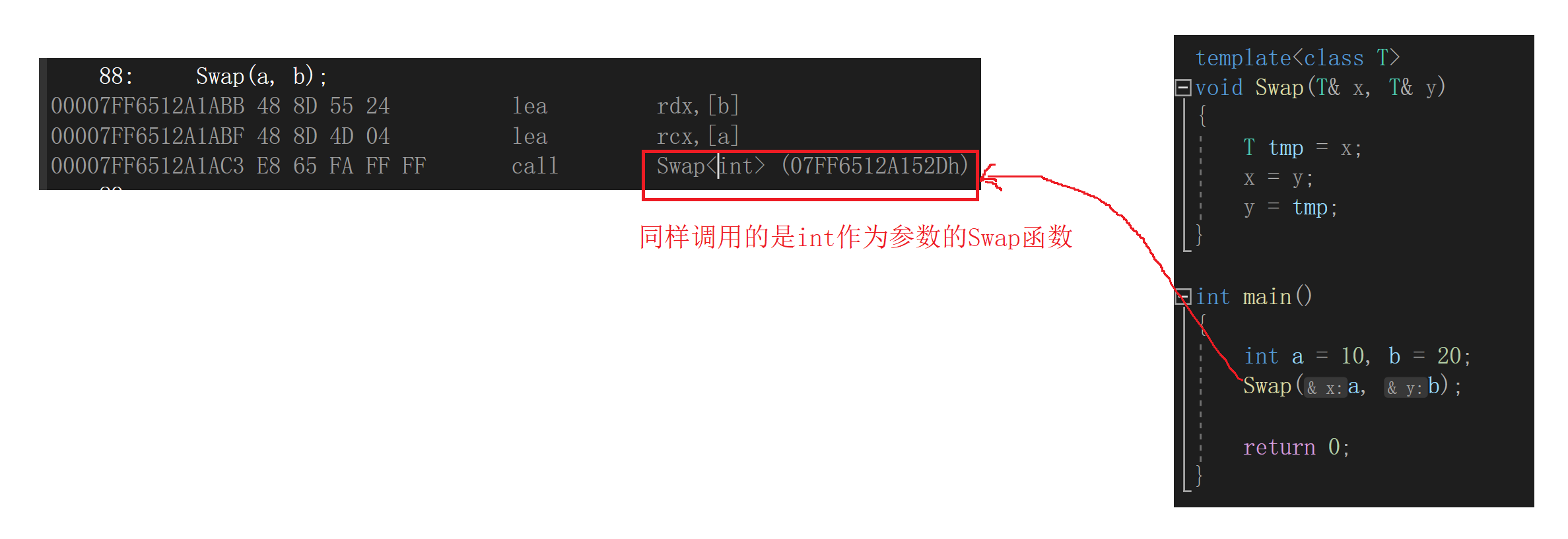
C++模板(一)
文章目录C模板(一)1. 泛型编程2. 函数模板2.1 函数模板格式2.2 模板原理2.3 模板实例化2.4 模板参数匹配原则3. 类模板3.1 类模板格式3.2 背景3.3 类模板的实例化C模板(一) 1. 泛型编程 前面我们学到了函数重载这个特性…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
