(树) 剑指 Offer 34. 二叉树中和为某一值的路径 ——【Leetcode每日一题】
❓ 剑指 Offer 34. 二叉树中和为某一值的路径
难度:中等
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
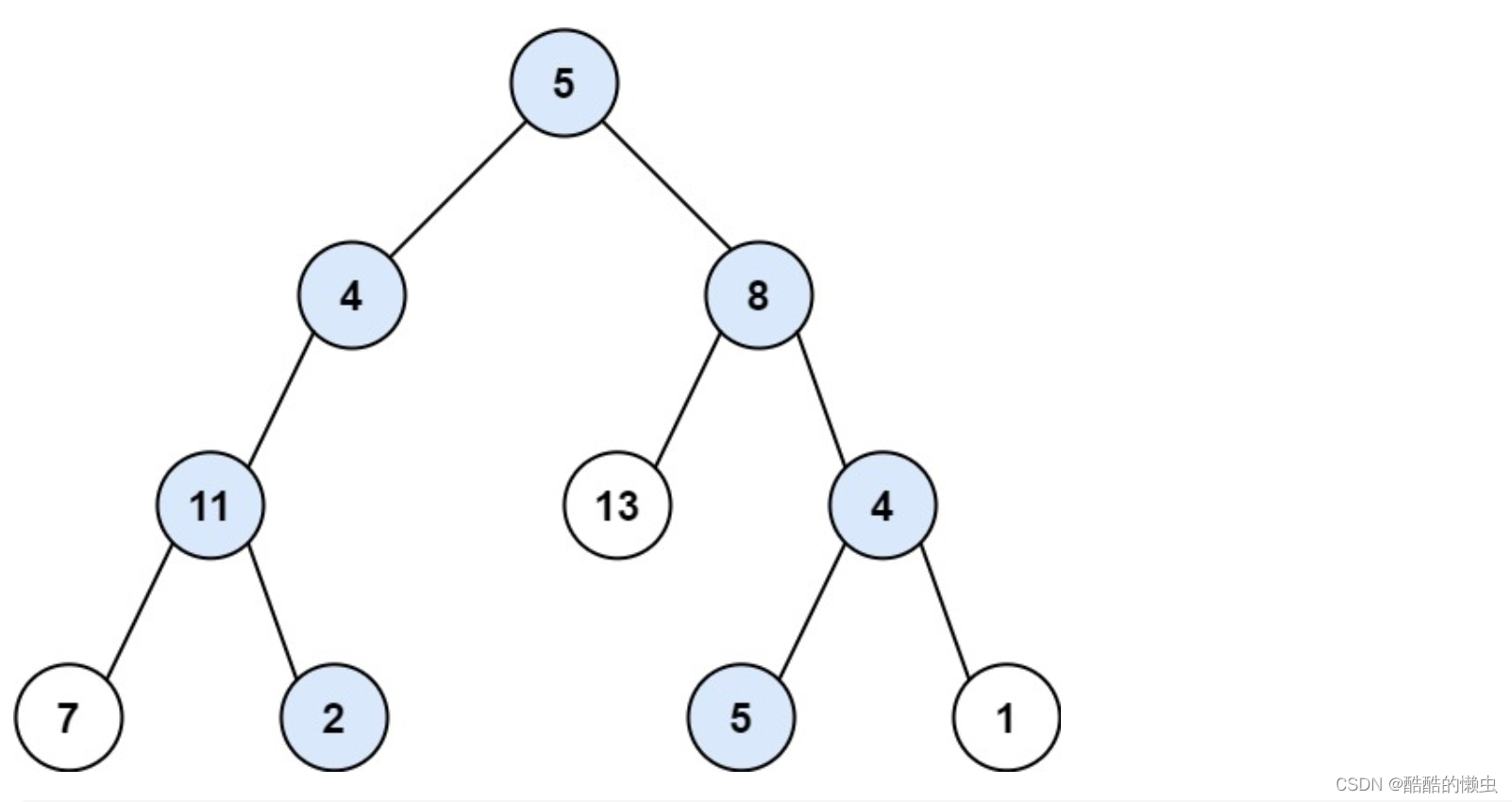
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:

输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
注意:本题与 113. 路径总和 II 相同。
💡思路:dfs
深度优先搜索的方式,枚举每一条从根节点到叶子节点的路径。
- 当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径,将 数组
tmp加入ans。 - 返回时,要删除当前数组
tmp最后一个元素。
🍁代码:(C++、Java)
C++
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:vector<vector<int>> ans;void path(TreeNode* root, vector<int>& tmp, int sum){if(root == nullptr) return;sum -= root->val;tmp.push_back(root->val);if(sum == 0 && root->left == nullptr && root->right == nullptr) {ans.push_back(tmp);}else{path(root->left, tmp, sum);path(root->right, tmp, sum);}tmp.pop_back();return;}
public:vector<vector<int>> pathSum(TreeNode* root, int target) {vector<int> tmp;path(root, tmp, target);return ans;}
};
Java
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {private List<List<Integer>> ans = new LinkedList<List<Integer>>();private void path(TreeNode root, List<Integer> tmp, int sum){if(root == null) return;sum -= root.val;tmp.add(root.val);if(sum == 0 && root.left == null && root.right == null) {ans.add(new LinkedList(tmp));}else{path(root.left, tmp, sum);path(root.right, tmp, sum);}tmp.remove(tmp.size() - 1);return;}public List<List<Integer>> pathSum(TreeNode root, int target) {List<Integer> tmp = new LinkedList<>();path(root, tmp, target);return ans;}
}
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2),其中
n为树的节点数。在最坏情况下,树的上半部分为链状,下半部分为完全二叉树,并且从根节点到每一个叶子节点的路径都符合题目要求。此时,路径的数目为 O ( n ) O(n) O(n),并且每一条路径的节点个数也为 O ( n ) O(n) O(n),因此要将这些路径全部添加进答案中,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。 - 空间复杂度: O ( n ) O(n) O(n),空间复杂度主要取决于栈空间的开销,栈中的元素个数不会超过树的节点数。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

(树) 剑指 Offer 34. 二叉树中和为某一值的路径 ——【Leetcode每日一题】
❓ 剑指 Offer 34. 二叉树中和为某一值的路径 难度:中等 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:…...

HDFS集群滚动升级以及回滚相关
HDFS集群滚动升级以及回滚相关 介绍不停机滚动升级非联邦HA集群联邦HA集群 停机升级--非HA集群HDFS集群降级和回滚异同点共同点不同点 HA集群降级(downgrade)注意事项 集群回滚操作 介绍 在hadoop v2中,HDFS支持namenode高可用(H…...
【LeetCode】094. 分割回文串II
文章目录 1. 解题思路1.1 创建dp表1.2 状态转移方程1.3 提前求出所有子串是否是回文串 2. 整体代码 1. 解题思路 1.1 创建dp表 这道题我们使用动态规划的方法来解,首先创建一个大小为字符串长度的dp表。dp[i] 表示 s[0, i] 的字符串最小划分多少次可以全划分为回文…...
CBCGPRibbon 添加背景图片
resource.h中声明资源的ID:ID_RIBBON_BACKIMAGE rc文件中添加png图片路径: ID_RIBBON_BACKIMAGE PNG DISCARDABLE "res\\bkribbon.png" 代码中添加下测: //添加背景图片 m_wndRibbonBar.SetBackgroundImage(ID_RIB…...

无涯教程-Perl - last 语句函数
当在循环内遇到 last 语句时,循环立即终止,程序控制在循环后的下一条语句处恢复。您可以为LABEL提供最后一个语句,其中LABEL是循环的标签。 last 语句可以在嵌套循环内使用,如果未指定LABEL,则该语句将适用于最近的循环…...

网络安全 Day13-Linux三剑客awk知识
Linux三剑客awk知识 1. awk 介绍2. awk 语法3. 练习 1. awk 介绍 awk 是一门语言, 也是一个命令,Linux 有三剑客命令: grep/sed/awk三剑客的特长 grep 过滤内容sed 取行awk 取列 2. awk 语法 取列 取第一列文件($1): awk {print $1} 文件指定分隔符为文件: awk -F "指…...
java讲解Spring Boot配置文件级别 相互覆盖关系 解决一方不愿意给数据库密码 一方不愿意给源码时 数据库配置问题
前面 我们讲过Spring Boot 修改临时变量的方式 但另一个场景 就是 我们 在本地开发环境 用的是一个配置 但如果项目经理上线 他想改这些配置 怎么弄呢 特别是数据库之类的配置 很多线上是不太一样的 那么 我们先看一个比较基本的方法 在配置文件的同目录下创建一个目录 叫 con…...

点击表格行高亮
css中三元表达式 :class"[activeIndex index ? color : , item]"点击行高亮 <div click"actvied(index)" :class"[activeIndex index ? color : , item]"v-for"(item, index) in tableData" :key"index">{{ item…...
基于粒子群优化算法的配电网光伏储能双层优化配置模型[IEEE33节点](选址定容)(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码、数据、讲解 💥1 概述 由于能源的日益匮乏,电力需求的不断增长等,配电网中分布式能源渗透率不断提高,且逐渐向主动配电网方…...
零代码爬虫平台SpiderFlow的安装
什么是 Spider Flow ? Spider Flow 是一个高度灵活可配置的爬虫平台,用户无需编写代码,以流程图的方式,即可实现爬虫。该工具支持多数据源、自动保存至数据库、任务监控、抓取 JS 动态渲染页面、插件扩展(OCR 识别、邮…...

Java 与其他编程语言:比较分析
Java 擅长可移植性和可靠性,Python 擅长通用性和简单性,JavaScript 擅长 Web 开发,C 擅长性能,Go 擅长效率。 在广阔的软件开发世界中,选择正确的编程语言对于任何项目的成功都至关重要。Java 是一种以其多功能性和可移…...
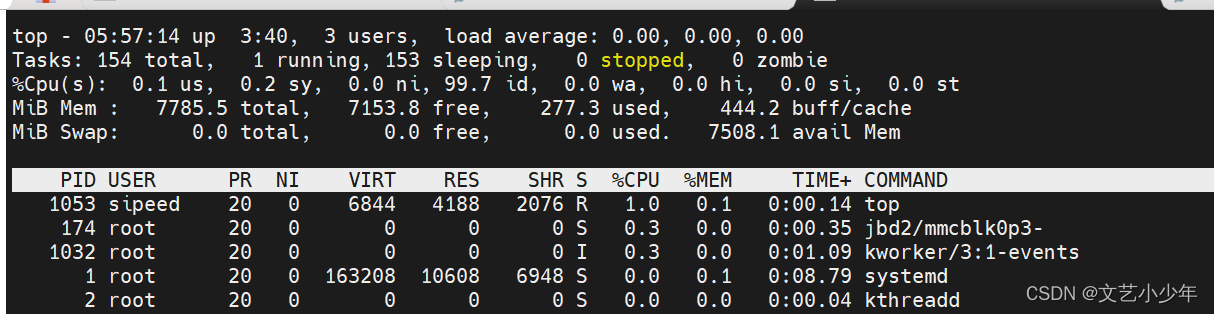
Linux性能分析工具介绍(二)--内存、进程、磁盘、IO分析
目录 一、引言 二、Linux性能分析工具介绍 ------>2.1、进程 ------>2.2、内存 ------>2.3、磁盘 ------>2.4、IO 一、引言 本章从内存、IO、进程的角度,分析linux系统的性能 二、Linux性能分析工具介绍 2.1、进程 2.1.1、top top命令可以动态查看进程…...

海外热门地区/国家常见主体证件示例
海外热门地区/国家常见主体证件示例(本页面内容较多,你可以通过CtrlF搜索) Overseas Popular Areas / Countries Examples of Common certificates (This page has more content, you can search by CtrlF) 中国香港…...
【阵列信号处理】空间匹配滤波器、锥形/非锥形最佳波束成形器、样本矩阵反演 (SMI) 研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
使用MPU6050计算方向盘角度
我给你们作了榜样、叫你们照着我向你们所作的去作。 ——【约翰福音13:15】 1.前言 前段时间接到一个项目需求:使用现有的陀螺仪MPU6050实现计算当前车辆的方向盘角度。 2.需求分析 MPU6050可获取三轴角速度和三轴加速度,并通过算法可以获得横滚角、…...

区块链实验室(13) - 在PBFT中节点的度与其流量的特征
前面若干实验说明了PBFT的耗时、流量与度的特征,见 区块链实验室(10) - 实例说明PBFT的共识过程, 区块链实验室(11) - PBFT耗时与流量特征, 区块链实验室(12) - 网络拓扑对PBFT共识流量的影响 同样的实验方案,在100个节点构成的无标度网络中完成100次交…...

C++——文件操作
一、文本文件 C中输入输出是通过流对象进行操作,对于文件来说写文件就是将内容从程序输出到文件,需要用到写文件流ofstream;而读文件就是将内容从文件输入到程序,需要用到读文件流ifstream;这两个文件流类都包含在头文…...

channel通道笔记
channel通道笔记 介绍 语法 1.一般使用make创建channel(常用) c : make(chan datatype),datatype是数据类型 2.直接显示声明,创建的值为空,一般没有太大意义 var c chan datatype 三种定义写法: 既可以收数据又可以发数据:chan datatype只可以收数据:chan <- datatype只可…...

无涯教程-Lua - 面向对象
面向对象编程(OOP)是现代编程时代中使用最广泛的编程技术之一。 OOP的特征 类(Class) - 类是用于创建对象的可扩展模板。 对象(Objects) - 它是类的实例,并为其分配了单独的内存空间。 继承(Inheritance) - 这是一个概…...

Java中的IOUtils是什么?
Java中的IOUtils是一个工具类,用于简化文件和流的操作。它提供了一些常用的方法,如复制文件、读取文件、写入文件等。 下面是一个简单的示例,演示如何使用IOUtils来复制文件: import org.apache.commons.io.FileUtils; import j…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
