搜索与图论(三)
一、最小生成树
1.1Prim算法
朴素版Prim
一般用于稠密图
算法流程:
集合表示当前已经在连通块的点
1.初始化距离,把所有距离都初始化为正无穷
2.n次迭代,找到集合外距离最小的点 ->t
3.用t来更新其它点到集合的距离
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 510,INF = 0x3f3f3f3f;int n,m;
int g[N][N];
int dist[N];
bool st[N];int prim()
{memset(dsit,0x3f,sizeof dsit);int res = 0;for(int i = 0;i < n;i ++){int t = -1;for(int j = 1;j <= n;j ++){if(! st[j] && (t == -1 || dist[t] > dist[j]))t = j;}if(i && dist[t] == INF) return INF;for(int j = 1;j <=n;j ++) dist[j] = min(dist[j],g[t][j]);st[t] = true;}return res;
}
int main()
{scanf("%d%d",&n,&m);memset(g,0x3f,sizeof g);while(m --){int a,b,c;scanf("%d%d%d",&a,&b,&c);g[a][b] = g[b][a] = min(g[a][b],c);}int t = prim();if(t == INF) puts("impossible");else printf("%d\n",t);return 0;
}1.2Kruskal算法
一般用于稀疏图
算法流程:
1.将所有边按照权重从小到大排序
2.枚举每一条边(a,b),权重为c
如果(a,b)不连通,则将这条边加入集合中
#include<iostream>
#include<algorithm>using namespace std;const int N = 100010;int n,m;
//并查集的集合
int p[N];struct Edge
{int a,b,w;bool operator < (const Edge &W)const{return w < W.w;}
}edges[N];int find(int x)
{if(p[x] != x) p[x] = find(p[x]);return p[x];
}
int main()
{scanf("%d%d",&n,&m);for(int i = 0;i < m;i ++){int a,b,w;scanf("%d%d%d",&a,&b,&w);edges[i] = {a,b,w};}sort(edges,edges + m);for(int i = 1;i <= n;i ++) p[i] = i;int res = 0,cnt = 0;for(int i = 0; i < m; i ++){//从小到大枚举所有边int a = edges[i].a,b = edges[i].b,w = edges[i].w;//知道a与b的祖宗节点a = find(a),b = find(b);//判断a与b是否连通if(a != b){//集合合并p[a] = b;res += w;cnt ++;}}if (cnt < n - 1) puts("impossible");else printf("%d\n",res);return 0;
}
二、二分图
二分图当且仅当图中不含奇数环
2.1染色法
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 100010,M = 200010;int n,m;
int h[N],e[M],ne[M],idx;
int color[N];void add(int a,int b)
{e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}bool dfs(int u,int c)
{//当前点的颜色是ccolor[u] = c;for(int i = h[u];i != -1;i = ne[i]){int j = e[i];if(!color[j]){if(!dfs(j,3 - c)) return false;}else if (color[j] == c) return false;}return true;
}int main()
{scanf("%d%d",&n,&m);memset(h,-1,sizeof h);while(m --){int a,b;scanf("%d%d",&a,&b);add(a,b),add(b,a);}bool flag = true;for(int i = 1;i <=n;i ++){if(!color[i]){if(!dfs(i,1)){flag = false;break;}}}if(flag) puts("Yes");else puts("No");return 0;
}
2.2匈牙利算法
#include<iostream>
#include<algorithm>
#include<cstring>using namespace std;const int N = 510,M = 100010;int n1,n2,m;
int h[N],e[M],ne[M],idx;
int match[N];
bool st[N];void add(int a,int b)
{e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}
bool find(int x)
{for(int i = h[x];i != -1;i = ne[i]){int j = e[i];if(!st[j]){st[j] = true;if(match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}
int main()
{scanf("%d%d%d",&n1,&n2,&m);memset(h,-1,sizeof h);while(m --){int a,b;scanf("%d%d",&a,&b);add(a,b);}int res = 0;for(int i = 0;i <= n1;i ++){memset(st,false,sizeof st);if(find(i)) res ++;}printf("%d\n",res);return 0;
}
相关文章:
)
搜索与图论(三)
一、最小生成树 1.1Prim算法 朴素版Prim 一般用于稠密图 算法流程: 集合表示当前已经在连通块的点 1.初始化距离,把所有距离都初始化为正无穷 2.n次迭代,找到集合外距离最小的点 ->t 3.用t来更新其它点到集合的距离 #include<iostream> #include&…...

阿里云“通义千问”开源,可免费商用
我是卢松松,点点上面的头像,欢迎关注我哦! 阿里云成为国内首个加入大模型开源行列的大型科技企业。就在昨天,阿里云公开表态,把自家的通义千问大模型开源。 阿里云把通用70亿参数模型,包括Qwen-7B和对话模…...

23.7.31 牛客暑期多校5部分题解
E - Red and Blue and Green 题目大意 构造一个长度为 n n n 的序列,满足 m m m 个条件,每个条件包含三个数 l , r , w l,\space r,\space w l, r, w,表示区间左端点,区间右端点,这个区间的逆序对数的奇偶性&…...
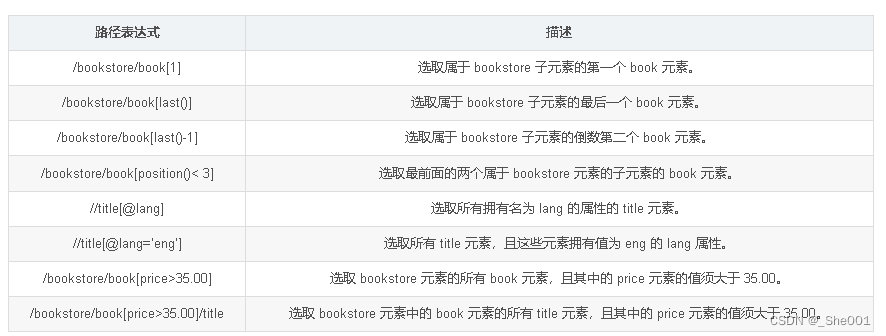
Python爬虫的学习day02 requests 模块post 函数, lmxl 模块的 etree 模块
1. requests 模块post 函数 1.1 post 函数的参数 (简单版) 参数1: url 网络地址 参数2: data 请求数据 (一般数据是 账号,密码) 参数3: headers 头请求 (…...

客户流失分析预测案例 -- 机器学习项目基础篇(7)
客户流失 它是指现有的客户、用户、订阅者或任何类型的回头客停止与公司开展业务或结束与公司的关系。 客户流失的类型 合同客户流失:当客户签订了服务合同并决定取消服务时,例如有线电视,SaaS。自愿流失:当用户自愿取消服务时…...

uniapp中我使用uni.navigateTo跳转webview页面传参,但是接收的参数只有一半。
在uniapp中使用uni.navigateTo跳转webview页面传参时,可能会遇到接收的参数只有一半的情况。这可能是因为在跳转时,url的长度超过了限制。为了解决这个问题,可以使用encodeURIComponent和decodeURIComponent进行编码和解码。 具体的解决办法…...

使用kaminari,在列表页实现分页功能
安装 1. bundller 大于1的话,可以使用这个版本 gem install kaminari -v 0.16.3 或者 gem kaminari 2. 使用命令: $ bundle install 3. 然后使用这个命令可以创建一个config文件 $ rails g kaminari:config 4. 重新启动服务器 bundle exec rail…...

Android 性能调优之bitmap的优化
背景 Android开发中,加载图片过多、过大很容易引起OutOfMemoryError异常,即我们常见的内存溢出。因为Android对单个应用施加内存限制,默认分配的内存只有几M(具体视不同系统而定)。而载入的图片如果是JPG之类的压缩格…...

HOT74-数组中的第K个最大元素
leetcode原题链接:数组中的第K个最大元素 题目描述 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O…...
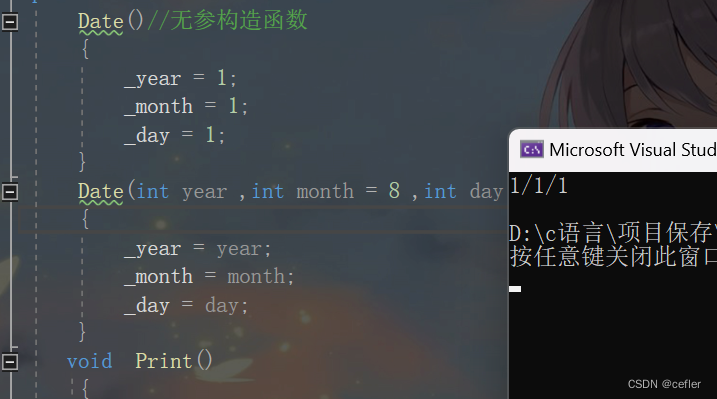
类与对象【中】
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析2 目录 👉🏻类的默认6个成员函数👉🏻构造…...
uni-app:实现列表单选功能
效果图: 核心解析: 一、 <view class"item_all" v-for"(item, index) in info" :key"index"><view classposition parameter-info text-over :classitem.checked?"checked_parameter":""…...
vue中axios二次封装并发起网络请求配置
1.安装axios npm i axios 2.导入 //对axios进行二次封装 import axios from "axios"// 创建axios实例,其实request就是axiosconst requests axios.create({// 发请求的时候自动出现api// baseURL:"api",// 请求超时的时间timeout:5000, })…...

开源全文搜索引擎汇总
1、Apache Lucene Java 全文搜索框架 许可证:Apache-2.0 开发语言:Java 官网:https://lucene.apache.org/。Apache Lucene 是完全用 Java 编写的高性能、功能齐全的全文检索引擎架构,提供了完整的查询引擎和索引引擎、部分文本分析引擎。目的是为软件开发人员提供一个简单…...
gitlab CI/CD 安装 gitlab runner
一、为什么需要安装gitlab runner ? 极狐GitLab Runner 极狐GitLab Runner 是在流水线中运行作业的应用,与极狐GitLab CI/CD 配合运作。 说白了就是你部署的一个agent。 二、如何安装? 1.介绍通过helm部署github runner 2.helm添加仓库 h…...

服务器中了malox勒索病毒后怎么办怎么解决,malox勒索病毒解密数据恢复
服务器遭受Malox勒索病毒攻击后,快速解密并恢复数据至关重要,以便减少更大的经济损失。近期,新的一波malox勒索病毒正在肆虐,我们收到很多企业的求助,企业的服务器数据库遭到了malox勒索病毒攻击,导致系统内…...
Python小白学习:超级详细的字典介绍(字典的定义、存储、修改、遍历元素和嵌套)
目录 一、字典简介1.1 创建字典1.2 访问字典中的值1.3 添加键值对1.4 修改字典中的值实例 1.5 删除键值对1.6 由多个类似对象组成的字典1.7 使用get()访问值1.8 练习题 二、遍历字典2.1 遍历所有键值对实例 2.2 遍历字典中的所有键2.3 按照特定顺序遍历字典中的所有键2.4 遍历字…...
word转pdf两种方式(免费+收费)
一、免费方式 优点:1、免费;2、在众多免费中挑选出的转换效果相对较好,并且不用像openOffice那样安装服务 缺点:1、对字体支持没有很好,需要安装字体库或者使用宋体(对宋体支持很好)2、对于使…...
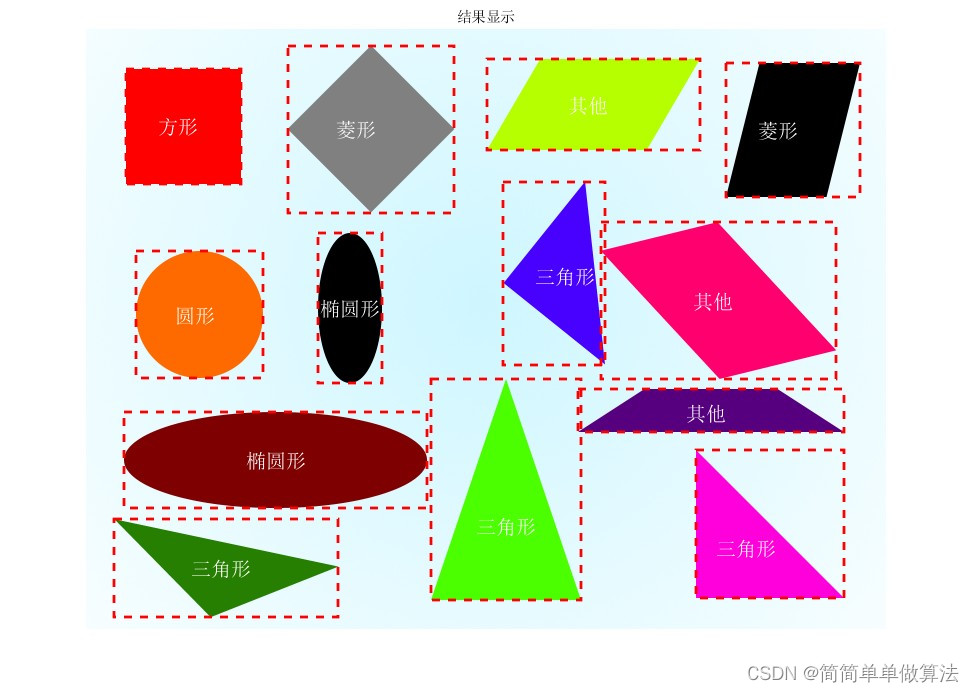
基于图像形态学处理的目标几何形状检测算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 .................................................... %二进制化图像 Images_bin imbinari…...

python系列教程211——map
朋友们,如需转载请标明出处:https://blog.csdn.net/jiangjunshow 声明:在人工智能技术教学期间,不少学生向我提一些python相关的问题,所以为了让同学们掌握更多扩展知识更好地理解AI技术,我让助理负责分享…...
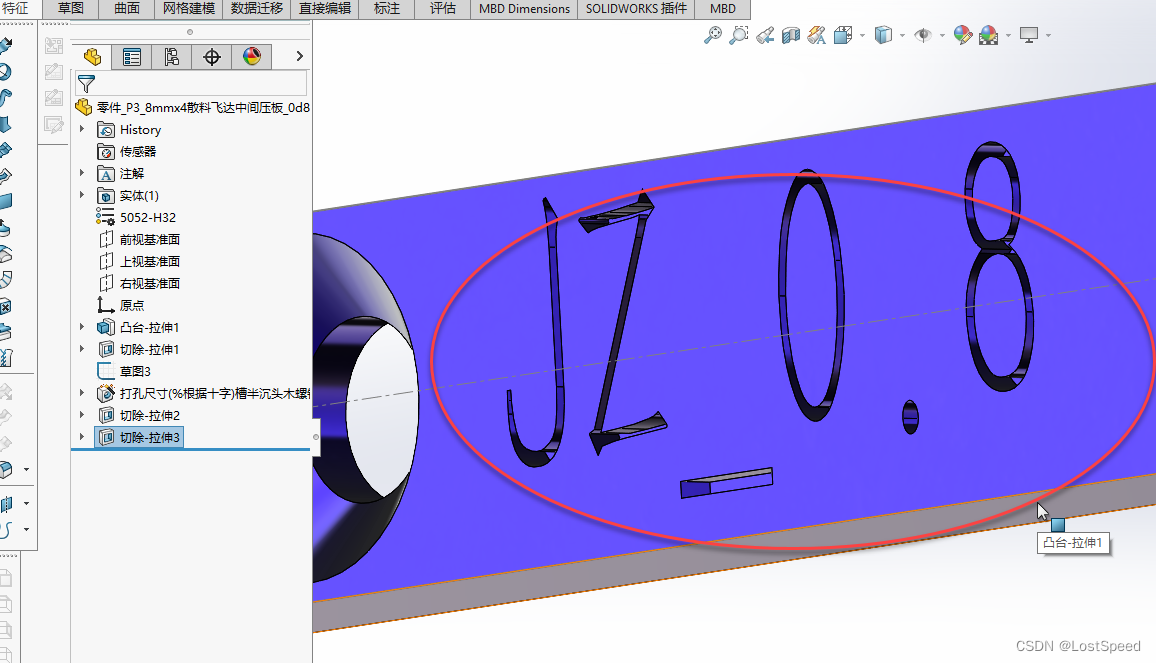
SW - 3D打印件最好带上浮雕文字标记
文章目录 SW - 3D打印件最好带上浮雕文字标记概述笔记END SW - 3D打印件最好带上浮雕文字标记 概述 做了一些散料飞达的压板, 下了3D打印的单. 一共有10种压板, 每种压板做的数量不等.压板分为2个大的类(中间压板, 边上的压板), 每个类中分了5个子类, 子类之间只是一个高度方…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
