Python实现决策树算法:完整源码逐行解析
决策树是一种常用的机器学习算法,它可以用来解决分类和回归问题。决策树的优点是易于理解和解释,可以处理数值和类别数据,可以处理缺失值和异常值,可以进行特征选择和剪枝等操作。决策树的缺点是容易过拟合,对噪声和不平衡数据敏感,可能不稳定等。
在这篇文章中,将介绍如何用 Python 实现决策树算法,包括以下几个步骤:
目录
一、导入所需的库和数据集
二、定义决策树的节点类和树类
三、定义计算信息增益的函数
四、定义生成决策树的函数
五、定义预测新数据的函数
六、测试和评估决策树的性能
一、导入所需的库和数据集
首先,我们需要导入一些常用的库,如 numpy, pandas, matplotlib 等,以及 sklearn 中的一些工具,如 train_test_split, accuracy_score 等。我们也需要导入一个用于测试的数据集,这里我们使用 sklearn 中自带的鸢尾花数据集(iris),它包含了 150 个样本,每个样本有 4 个特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度)和 1 个类别(setosa, versicolor, virginica)。我们可以用以下代码来实现:
# 导入所需的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 导入 sklearn 中的工具
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 导入鸢尾花数据集
iris = load_iris()
X = iris.data # 特征矩阵
y = iris.target # 类别向量
feature_names = iris.feature_names # 特征名称
class_names = iris.target_names # 类别名称# 查看数据集的基本信息
print("特征矩阵的形状:", X.shape)
print("类别向量的形状:", y.shape)
print("特征名称:", feature_names)
print("类别名称:", class_names)# 将数据集划分为训练集和测试集,比例为 7:3
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 查看训练集和测试集的大小
print("训练集的大小:", X_train.shape[0])
print("测试集的大小:", X_test.shape[0])
运行上述代码,我们可以得到以下输出:
特征矩阵的形状: (150, 4)
类别向量的形状: (150,)
特征名称: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
类别名称: ['setosa' 'versicolor' 'virginica']
训练集的大小: 105
测试集的大小: 45
二、定义决策树的节点类和树类
接下来,我们需要定义一个表示决策树节点的类 Node 和一个表示决策树本身的类 Tree。节点类的属性包括:
- feature:节点的划分特征的索引,如果是叶子节点,则为 None
- value:节点的划分特征的值,如果是叶子节点,则为 None
- label:节点的类别标签,如果是叶子节点,则为该节点所属的类别,如果是非叶子节点,则为该节点所包含的样本中最多的类别
- left:节点的左子树,如果没有,则为 None
- right:节点的右子树,如果没有,则为 None
树类的属性包括:
- root:树的根节点,初始为 None
- max_depth:树的最大深度,用于控制过拟合,初始为 None
- min_samples_split:树的最小分裂样本数,用于控制过拟合,初始为 2
我们可以用以下代码来实现:
# 定义决策树节点类
class Node:def __init__(self, feature=None, value=None, label=None, left=None, right=None):self.feature = feature # 节点的划分特征的索引self.value = value # 节点的划分特征的值self.label = label # 节点的类别标签self.left = left # 节点的左子树self.right = right # 节点的右子树# 定义决策树类
class Tree:def __init__(self, max_depth=None, min_samples_split=2):self.root = None # 树的根节点self.max_depth = max_depth # 树的最大深度self.min_samples_split = min_samples_split # 树的最小分裂样本数
三、定义计算信息增益的函数
为了生成决策树,我们需要选择一个合适的划分特征和划分值,使得划分后的子集尽可能地纯净。为了衡量纯净度,我们可以使用信息增益(information gain)作为评价指标。信息增益表示划分前后信息熵(information entropy)的减少量,信息熵表示数据集中不确定性或混乱程度的度量。信息增益越大,说明划分后数据集越纯净。
我们可以用以下公式来计算信息熵和信息增益:
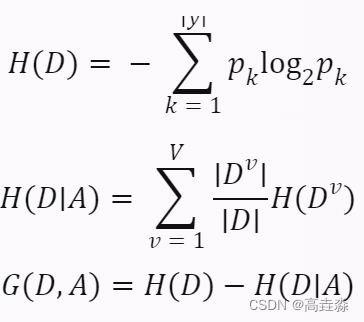
其中,
- D 表示数据集
- y 表示类别集合
- pk 表示第 k 个类别在数据集中出现的概率
- A 表示划分特征
- V 表示划分特征取值的个数
- Dv 表示划分特征取第 v 个值时对应的数据子集
我们可以用以下代码来实现:
# 定义计算信息熵的函数
def entropy(y):n = len(y) # 数据集大小labels_count = {} # 统计不同类别出现的次数for label in y:if label not in labels_count:labels_count[label] = 0labels_count[label] += 1ent = 0.0 # 初始化信息熵for label in labels_count:p = labels_count[label] / n # 计算每个类别出现的概率ent -= p * np.log2(p) # 累加信息熵return ent# 定义计算信息增益的函数
def info_gain(X, y, feature, value):n = len(y) # 数据集大小# 根据特征和值划分数据X_left = X[X[:, feature] <= value] # 左子集,特征值小于等于划分值的样本y_left = y[X[:, feature] <= value] # 左子集对应的类别X_right = X[X[:, feature] > value] # 右子集,特征值大于划分值的样本y_right = y[X[:, feature] > value] # 右子集对应的类别# 计算划分前后的信息熵和信息增益ent_before = entropy(y) # 划分前的信息熵ent_left = entropy(y_left) # 左子集的信息熵ent_right = entropy(y_right) # 右子集的信息熵ent_after = len(y_left) / n * ent_left + len(y_right) / n * ent_right # 划分后的信息熵,加权平均gain = ent_before - ent_after # 信息增益return gain
四、定义生成决策树的函数
接下来,我们需要定义一个生成决策树的函数,它的输入是训练数据和当前深度,它的输出是一个决策树节点。这个函数的主要步骤如下:
- 如果当前数据集为空,或者当前深度达到最大深度,或者当前数据集中所有样本属于同一类别,或者当前数据集中所有样本在所有特征上取值相同,或者当前数据集大小小于最小分裂样本数,则返回一个叶子节点,其类别标签为当前数据集中最多的类别。
- 否则,遍历所有特征和所有可能的划分值,计算每种划分方式的信息增益,并选择信息增益最大的特征和值作为划分依据。
- 根据选择的特征和值,将当前数据集划分为左右两个子集,并递归地生成左右两个子树。
- 返回一个非叶子节点,其划分特征和值为选择的特征和值,其左右子树为生成的左右子树。
我们可以用以下代码来实现:
# 定义生成决策树的函数
def build_tree(X, y, depth=0):# 如果满足终止条件,则返回一个叶子节点if len(X) == 0 or depth == max_depth or len(np.unique(y)) == 1 or np.all(X == X[0]) or len(X) < min_samples_split:label = np.argmax(np.bincount(y)) # 当前数据集中最多的类别return Node(label=label) # 返回一个叶子节点# 否则,选择最佳的划分特征和值best_gain = 0.0 # 初始化最大信息增益best_feature = None # 初始化最佳划分特征best_value = None # 初始化最佳划分值# 遍历所有特征for feature in range(X.shape[1]):# 遍历所有可能的划分值,这里我们使用特征的中位数作为候选值value = np.median(X[:, feature])# 计算当前特征和值的信息增益gain = info_gain(X, y, feature, value)# 如果当前信息增益大于最大信息增益,则更新最佳划分特征和值if gain > best_gain:best_gain = gainbest_feature = featurebest_value = value# 根据最佳划分特征和值,划分数据集为左右两个子集X_left = X[X[:, best_feature] <= best_value] # 左子集,特征值小于等于划分值的样本y_left = y[X[:, best_feature] <= best_value] # 左子集对应的类别X_right = X[X[:, best_feature] > best_value] # 右子集,特征值大于划分值的样本y_right = y[X[:, best_feature] > best_value] # 右子集对应的类别# 递归地生成左右两个子树left = build_tree(X_left, y_left, depth + 1) # 左子树,深度加一right = build_tree(X_right, y_right, depth + 1) # 右子树,深度加一# 返回一个非叶子节点,其划分特征和值为最佳划分特征和值,其左右子树为生成的左右子树return Node(feature=best_feature, value=best_value, left=left, right=right)
这样,我们就完成了决策树的生成过程。我们可以用以下代码来调用这个函数,并将生成的决策树赋给树类的根节点属性:
# 创建一个决策树对象
tree = Tree(max_depth=3) # 设置最大深度为 3# 用训练数据生成决策树,并将其赋给根节点属性
tree.root = build_tree(X_train, y_train)
五、定义预测新数据的函数
接下来,我们需要定义一个预测新数据的函数,它的输入是一个新的样本和一个决策树节点,它的输出是一个预测的类别标签。这个函数的主要步骤如下:
- 如果当前节点是叶子节点,则返回其类别标签。
- 否则,根据当前节点的划分特征和值,将新样本划分到左右两个子树中的一个,并递归地在该子树上进行预测。
- 返回预测结果。
我们可以用以下代码来实现:
# 定义预测新数据的函数
def predict(x, node):# 如果当前节点是叶子节点,则返回其类别标签if node.feature is None:return node.label# 否则,根据当前节点的划分特征和值,将新样本划分到左右两个子树中的一个,并递归地在该子树上进行预测if x[node.feature] <= node.value: # 如果新样本在当前节点划分特征上的取值小于等于划分值,则进入左子树return predict(x, node.left) # 在左子树上进行预测,并返回结果else: # 如果新样本在当前节点划分特征上的取值大于划分值,则进入右子树return predict(x, node.right) # 在右子树上进行预测,并返回结果
六、测试和评估决策树的性能
这样,我们就完成了决策树的预测过程。我们可以用以下代码来调用这个函数,并对测试数据进行预测,并计算预测的准确率:
# 创建一个空的列表,用于存储预测结果
y_pred = []# 遍历测试数据,对每个样本进行预测,并将结果添加到列表中
for x in X_test:y_pred.append(predict(x, tree.root))# 将列表转换为 numpy 数组,方便计算
y_pred = np.array(y_pred)# 计算并打印预测的准确率
acc = accuracy_score(y_test, y_pred)
print("预测的准确率为:", acc)
运行上述代码,我们可以得到以下输出:
预测的准确率为: 0.9777777777777777
可以看到,用 Python 实现的决策树算法在鸢尾花数据集上达到了接近 98% 的准确率,这说明我们的算法是有效和可靠的。当然,决策树算法还有很多其他的细节和优化,比如如何选择最佳的划分值,如何处理数值和类别特征,如何进行剪枝和正则化等。
相关文章:
Python实现决策树算法:完整源码逐行解析
决策树是一种常用的机器学习算法,它可以用来解决分类和回归问题。决策树的优点是易于理解和解释,可以处理数值和类别数据,可以处理缺失值和异常值,可以进行特征选择和剪枝等操作。决策树的缺点是容易过拟合,对噪声和不…...

Linux文本三剑客---grep、sed、awk
目录标题 1、grep1.1 命令格式1.2命令功能1.3命令参数1.4grep实战演练 2、sed2.1 认识sed2.2命令格式2.3常用选项options2.4地址定界2.5 编辑命令command2.6用法演示2.6.1常用选项options演示2.6.2地址界定演示2.6.3编辑命令command演示 3、awk3.1认识awk3.2常用命令选项3.3awk…...
局域网VoIP网络电话测试
0. 环境 ubuntu18或者ubuntu22 - SIP服务器 win10 - SIP客户端1 ubuntu18 - SIP客户端2 1. SIP服务器搭建asterisk 1.0 环境 虚拟机ubuntu18 或者ubuntu22 1.1 直接安装 sudo apt-get install asterisk 1.2 配置用户信息 分为两个部分,第一部分是修改genera…...
el-table 去掉边框(修改颜色)
原始: 去掉表格的border属性,每一行下面还会有一条线,并且不能再拖拽表头 为了满足在隐藏表格边框的情况下还能拖动表头,修改相关css即可,如下代码 <style lang"less"> .table {//避免单元格之间出现白…...

redis与MongoDB的区别
1.Redis与MongoDB的概念 1.1 MongoDB MongoDB 是由C语言编写的,是一个基于分布式文件存储的开源数据库系统。 在高负载的情况下,添加更多的节点,可以保证服务器性能。 MongoDB 旨在为WEB应用提供可扩展的高性能数据存储解决方案。 MongoDB …...

CSS设置高度
要设置 article.content 的恰当高度,您可以使用 CSS 来控制元素的外观。有几种方法可以设置元素的高度,具体取决于你的需求和布局。 以下是几种常见的方法: 1. 固定高度:你可以直接为 article.content 设置一个固定的高度值&…...

开源免费用|Apache Doris 2.0 推出跨集群数据复制功能
随着企业业务的发展,系统架构趋于复杂、数据规模不断增大,数据分布存储在不同的地域、数据中心或云平台上的现象越发普遍,如何保证数据的可靠性和在线服务的连续性成为人们关注的重点。在此基础上,跨集群复制(Cross-Cl…...

【docker】docker-compose服务编排
目录 一、服务编排概念二、docker compose2.1 定义2.2 使用步骤2.3 docker-compose安装2.4 docker-compose卸载 三、编排示例 一、服务编排概念 1.微服务架构的应用系统中一般包含若干个微服务,每个微服务一般都会部署多个实例,如果每个微服务都要手动启…...
EdgeBox_tx1_A200 PyTorch v1.9.0 环境部署
大家好,我是虎哥,今天远程帮助几个小伙伴在A200 控制器上安装PyTorch v1.9.0 torchvision v0.10.0,中间也是经历了很多波折,当然,大部分是网络问题和版本适配问题,所以完事后,将自己完整可用的过…...

【雕爷学编程】MicroPython动手做(33)——物联网之天气预报
天气(自然现象) 是指某一个地区距离地表较近的大气层在短时间内的具体状态。而天气现象则是指发生在大气中的各种自然现象,即某瞬时内大气中各种气象要素(如气温、气压、湿度、风、云、雾、雨、闪、雪、霜、雷、雹、霾等ÿ…...
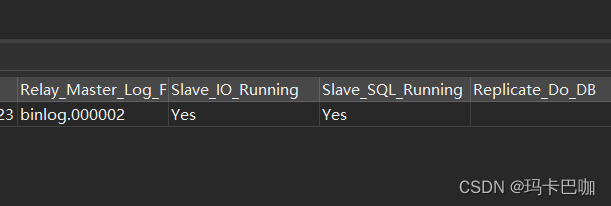
分库分表之基于Shardingjdbc+docker+mysql主从架构实现读写分离 (三)
本篇主要说明: 1. 因为这个mysql版本是8.0,所以当其中一台mysql节点挂掉之后,主从同步,甚至双向数据同步都失效了,所以本篇主要记录下当其中的节点挂掉之后如何再次生效。另外推荐大家使用mysql5.7的版本,这…...
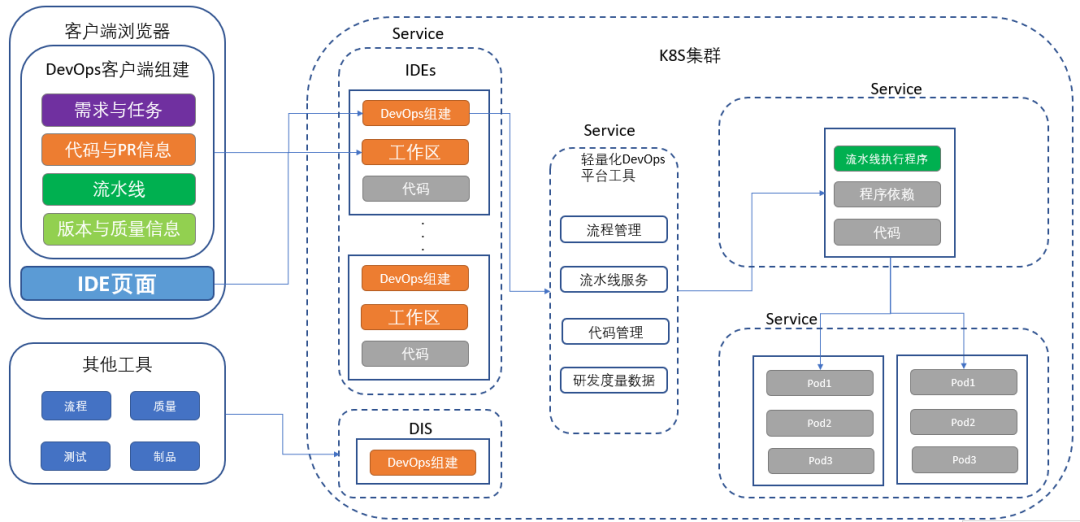
探秘企业DevOps一体化平台建设终极形态丨IDCF
笔者从事为企业提供研发效能改进解决方案相关工作十几年,为国内上百家企业提供过DevOps咨询及解决方案落地解决方案,涉及行业包括:金融、通信、制造、互联网、快销等多种行业。 DevOps的核心是研发效能改进,效能的提升离不开强大…...

百度智能创做AI平台
家人们好,在数字化时代,人工智能正引领着一场前所未有的创新浪潮。今天,我们将为大家介绍百度智能创做AI平台,这个为创意赋能、助力创作者的强大工具。无论你是创意工作者、内容创作者,还是想要释放内心创造力的个人&a…...

Python 开发工具 Pycharm —— 使用技巧Lv.1
Basic code completion Ctrl空格 is available in the search field when you search for text in the current file CtrlF, so there is no need to type the entire string 基本代码完成Ctrl 空格可在搜索领域当你搜索文本在当前文件Ctrl F,所以没有必要整个字符串类型 To m…...

zookeeper --- 高级篇
一、zookeeper 事件监听机制 1.1、watcher概念 zookeeper提供了数据的发布/订阅功能,多个订阅者可同时监听某一特定主题对象,当该主题对象的自身状态发生变化时(例如节点内容改变、节点下的子节点列表改变等),会实时、主动通知所有订阅者 …...

TypeScript【enum 枚举】
导语 在 TypeScript 中,新增了很多具有特性的一些数据类型处理方法,enum 【枚举】就是其中,很具有代表性的一种,所以本章节就来聊聊 在 TypeScript 中如何去运用 enum 【枚举】。 枚举的概念: 枚举(Enum&am…...
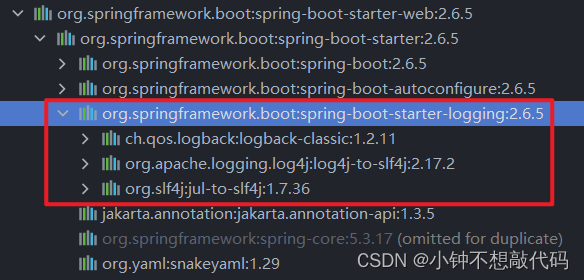
SpringBoot项目增加logback日志文件
一、简介 在开发和调试过程中,日志是一项非常重要的工具。它不仅可以帮助我们快速定位和解决问题,还可以记录和监控系统的运行状态。Spring Boot默认提供了一套简单易用且功能强大的日志框架logback,本文将介绍如何在Spring Boot项目中配置和…...
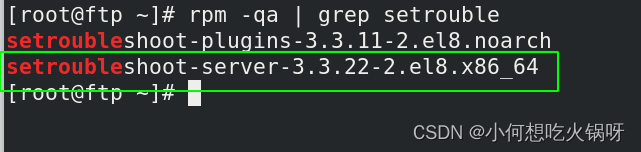
复习之selinux的管理
一、什么是selinux? SELinux,Security Enhanced Linux 的缩写,也就是安全强化的 Linux,是由美国国家安全局(NSA)联合其他安全机构(比如 SCC 公司)共同开发的,旨在增强传统 Linux 操…...

无涯教程-Lua - 文件I/O
I/O库用于在Lua中读取和处理文件。 Lua中有两种文件操作,即隐式(Implicit)和显式(Explicit)操作。 对于以下示例,无涯教程将使用例文件test.lua,如下所示。 -- sample test.lua -- sample2 test.lua 一个简单的文件打开操作使用以下语句。…...

java+ssm民宿酒店客房推荐预订系统_2k78b--论文
摘 要 互联网日益成熟,走进千家万户,改变多个行业传统的工作方式。民宿推荐管理以用户需求为基础,借由发展迅猛的互联网平台实现民宿推荐管理的信息化,简化旧时民宿推荐管理所需的纸质记录这一繁杂过程,从而大幅提高民…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
