Acwing.877 扩展欧几里得算法
题目
给定n对正整数ai , bi,对于每对数,求出一组ai ,g,使其满足ai* xi+ bi * yi = gcd(ai ,bi)。
输入格式
第一行包含整数n。
接下来n行,每行包含两个整数ai , bi。
输出格式
输出共n行,对于每组ai, bi,求出一组满足条件的axi, Ji,每组结果占一行。本题答案不唯一,输出任意满足条件的xi,yi均可。
数据范围
1 ≤n≤105,
1≤ai,bi≤ 2* 109
- 输入样例:
2
4 6
8 18
- 输出样例
-1 1
-2 1
题解
#include <iostream>
using namespace std;
int exgcd(int a,int b,int &x, int &y)
{if (!b){ x = 1, y = 0;return a; }int d = exgcd(b,a % b, y, x);y -= a / b * x;return d;
}
int main( )
{int n;scanf("%d",&n);while (n -- ){int a, b, x,y;scanf("%d%d", &a,&b);exgcd(a,b,x,y);printf("%d %d\n", x, y);} return 0;思路
在欧几里得算法的基础上进行公式推导
具体推导如下图

相关文章:

Acwing.877 扩展欧几里得算法
题目 给定n对正整数ai , bi,对于每对数,求出一组ai ,g,使其满足ai* xi bi * yi gcd(ai ,bi)。 输入格式 第一行包含整数n。 接下来n行,每行包含两个整数ai , bi。 输出格式 输出共n行,对于每组ai, bi,…...
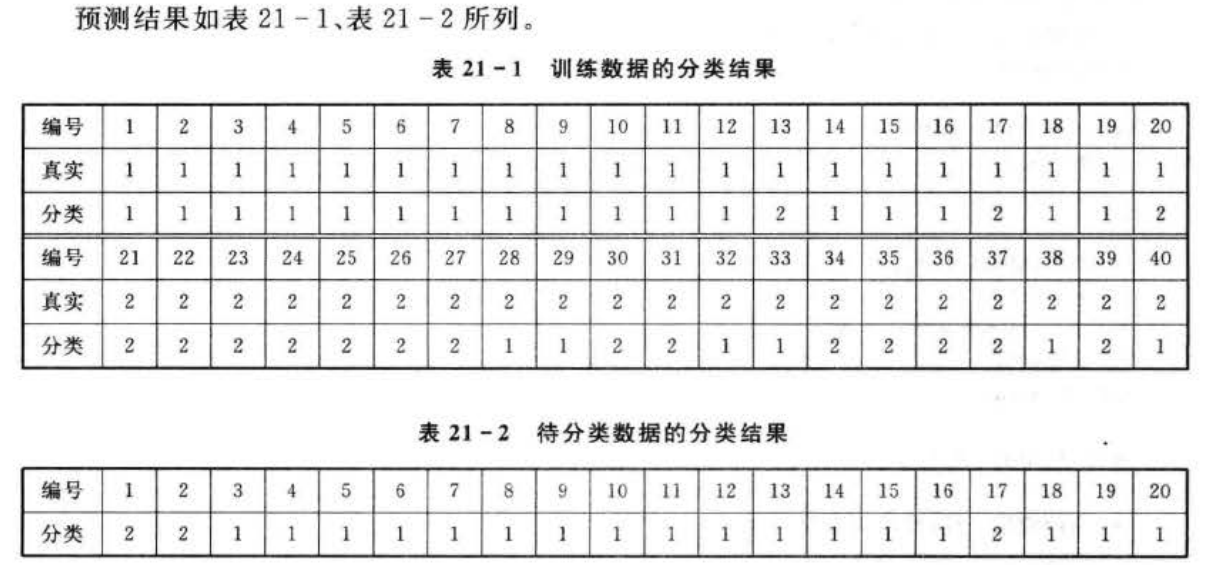
基于自组织竞争网络的患者癌症发病预测(matlab代码)
1.案例背景 1.1自组织竞争网络概述 前面案例中讲述的都是在训练过程中采用有导师监督学习方式的神经网络模型。这种学习方式在训练过程中,需要预先给网络提供期望输出,根据期望输出来调整网络的权重,使得实际输出和期望输出尽可能地接近。但是在很多情况下,在人们认知的过程中…...

golang mongodb
看代码吧 package main// 链接案例 https://www.mongodb.com/docs/drivers/go/current/fundamentals/connection/#connection-example // 快速入门 https://www.mongodb.com/docs/drivers/go/current/quick-start/ import ("context""fmt""log"…...
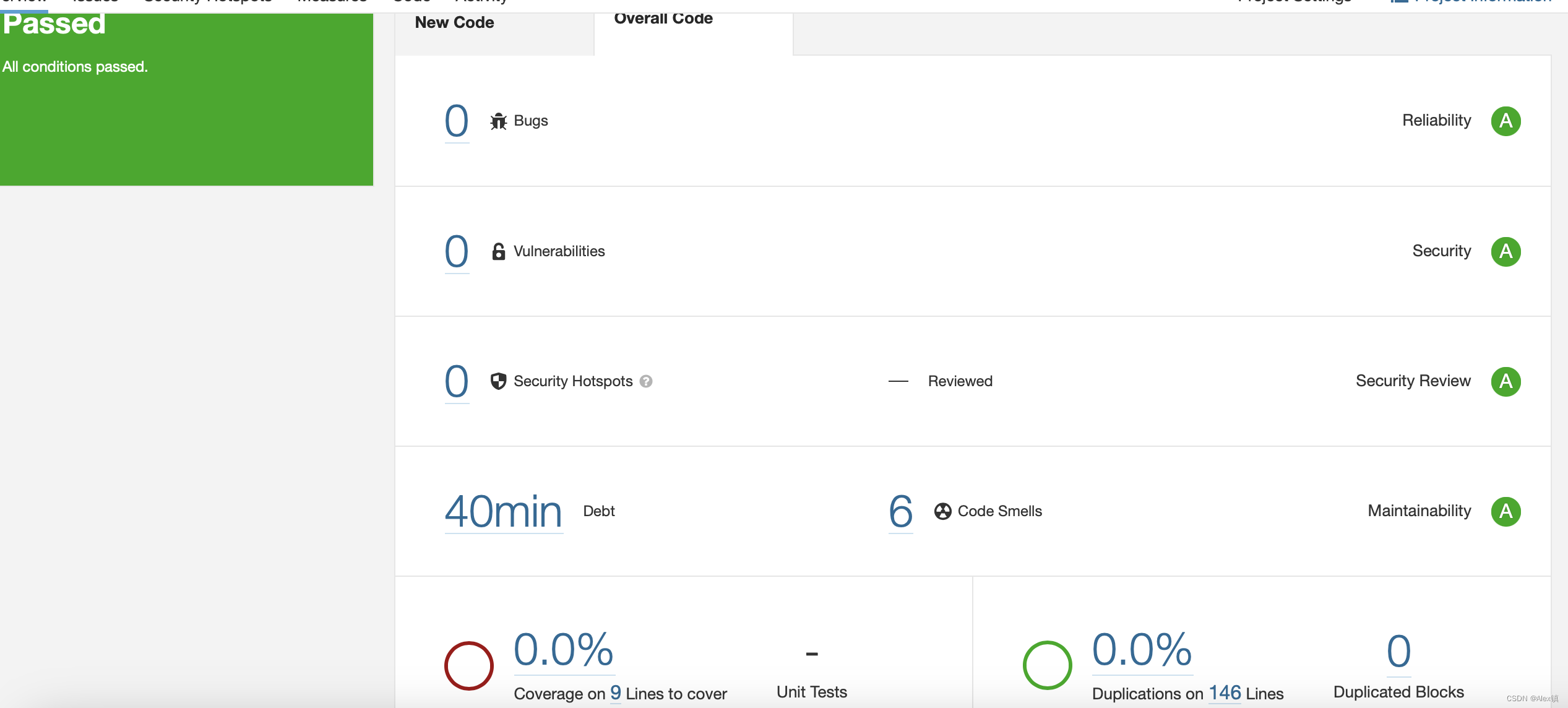
docker中的jenkins去配置sonarQube
docker中的jenkins去配置sonarQube 1、拉取sonarQube macdeMacBook-Pro:~ mac$ docker pull sonarqube:8.9.6-community 8.9.6-community: Pulling from library/sonarqube 8572bc8fb8a3: Pull complete 702f1610d53e: Pull complete 8c951e69c28d: Pull complete f95e4f8…...

企业如何实现自己的AI垂直大模型
文章目录 为什么要训练垂直大模型训练垂直大模型有许多潜在的好处训练垂直大模型也存在一些挑战 企业如何实现自己的AI垂直大模型1.确定需求2.收集数据3.准备数据4.训练模型5.评估模型6.部署模型 如何高效实现垂直大模型 ✍创作者:全栈弄潮儿 🏡 个人主页…...

Maven可选依赖和排除依赖简单使用
可选依赖 可选依赖指对外隐藏当前所依赖的资源 在maven_04_dao的pom.xml,在引入maven_03_pojo的时候,添加optional <dependency><groupId>com.rqz</groupId><artifactId>maven_03_pojo</artifactId><version>1.0-SNAPSHOT&…...

“深入探索JVM:Java虚拟机的工作原理解析“
标题:深入探索JVM:Java虚拟机的工作原理解析 摘要:本文将深入探索Java虚拟机(JVM)的工作原理,从类加载、内存管理、垃圾回收、即时编译器等方面进行详细解析,帮助读者更好地理解JVM的内部机制。…...

Prometheus-各种exporter
文章目录 一、 nginx-prometheus-exporter1 nginx 配置1.1 Nginx 模块支持1.2 Nginx 配置文件配置2 部署 nginx-prometheus-exporter2.1 二进制方式部署2.1.1 解压部署2.1.2 配置 systemd2.1.3 添加 prometheus 的配置2.1.4 Dashborad2.2 docker-compose 方式部署3 可配置的指标…...
小程序的 weiui的使用以及引入
https://wechat-miniprogram.github.io/weui/docs/quickstart.html 网址 1.点进去,在app.json里面配置 在你需要的 页面的 json里面配置,按需引入 然后看文档,再在你的 wxml里面使用就好了...
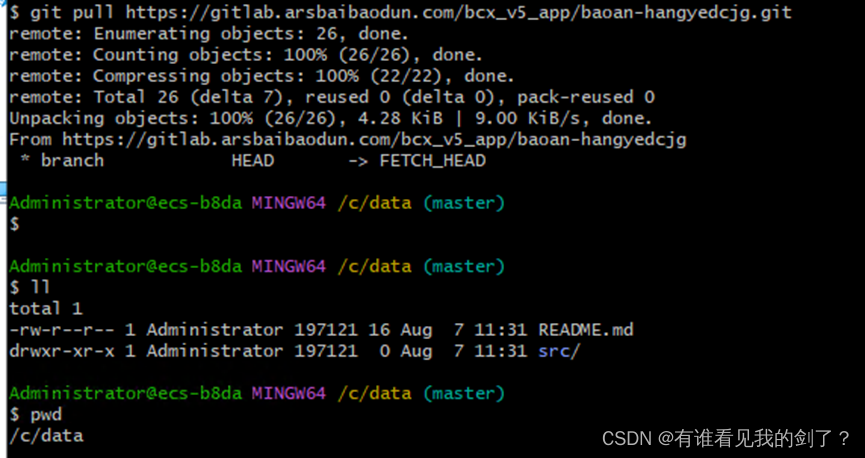
git目录初始化,并拉取最新代码
现有C:\data目录,将目录初始化,并拉取代码在这里插入代码片 https://gitlab.arsbaibaodun.com/bcx_v5_app/baoan-hangyedcjg.git 1、 git init生成 .git 目录即目录初始化完成,可以进行拉取代码 代码成功拉取到了data目录,默认…...
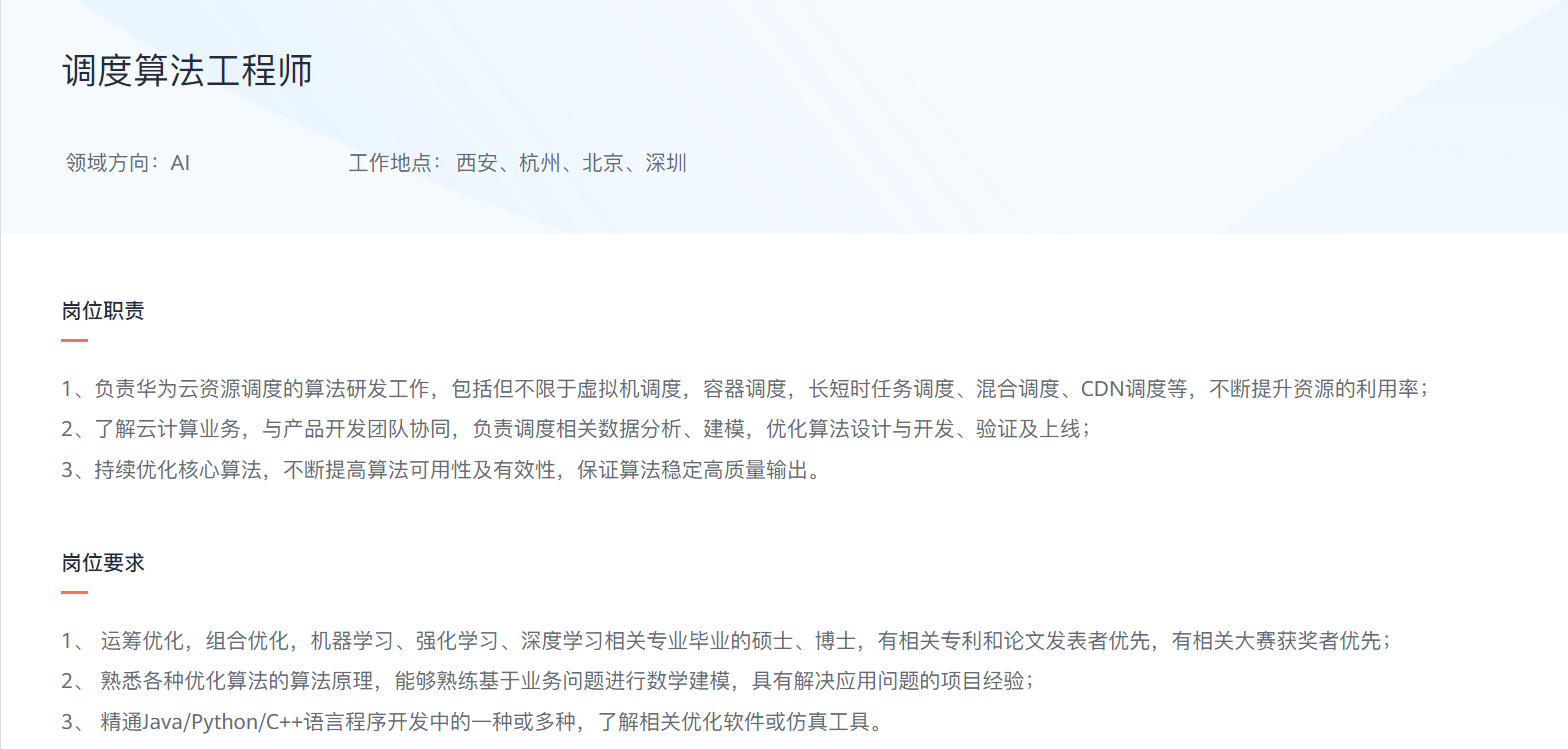
运筹调度算法工程式招聘情况:技能要求、薪资、工作地
目录 一、前言二、岗位信息三、总结 一、前言 前一段时间,常看到运筹学的老师们在朋友圈转发下面的图片。今天忽然想起这件事,顺势查了一下“调度算法工程师”在Boss直聘上的岗位信息,也整理一下招聘企业所需的“调度”技能。 二、岗位信息…...

css2-BFC是什么?
1、BFC是什么? 在页面布局时,经常会出现以下几种情况: 这个元素高度怎末没了? 这两栏布局怎末没法自适应? 这两个元素的间距怎末有点奇怪的样子? … 原因就是元素之间互相影响,导致了意料之外的…...
库操作)
Flutter Dart语言(04)库操作
0 说明 该系列教程主要是为有一定语言基础 C/C的程序员,快速学习一门新语言所采用的方法,属于在C/C基础上扩展新语言的模式。 1 自定义库 & 系统自定义库 引入代码如下所示: import xxx.dart; //自定义库引入,xxx为本…...

通向架构师的道路之漫谈使用ThreadLocal改进你的层次的划分
一、什么是ThreadLocal 早在JDK 1.2的版本中就提供java.lang.ThreadLocal,ThreadLocal为解决多线程程序的并发问题提供了一种新的思路。使用这个工具类可以很简洁地编写出优美的多线程程序。 ThreadLocal很容易让人望文生义,想当然地认为是一个“本地线…...

springboot全局统一返回处理
文章目录 前言一、统一的返回格式二、全局异常处理三、全局返回处理(装逼用的)总结 前言 项目中一般都会有规定好的接口返回格式,无论成功与失败,一般格式都是不变的,这样是为了方便前后端统一处理,今天就来说下前后端统一处理的较为优雅的方式; 一、统一的返回格式 一般而言…...
)
C/C++面试经历(一)
目录 1. 说说你对C与C的认识? 2. 说说C的三大特性? 3. 说说C的重载? 4. C语言为什么不支持重载? 5. 说说类的默认成员函数? 6. 类的构造函数为什么不支持虚函数? 7. 说说你对指针和引用的理解&…...

【PostgreSQL】系列之 一 用户创建和授权(三)
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,Java基础学习,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的…...

Python连接Hive实例教程
一 Python连接hive环境实例 经在网络查询相关的教程,发现有好多的例子,发现连接底层用的的驱动基本都是pyhive和pyhs2两种第三方库的来连接的 hive,下面将简介windows 10 python 3.10 连接hive的驱动程序方式,开发工具:pycharm …...

Jest和Mocha对比:两者之间有哪些区别?
目录 什么是单元测试? Jest和Mocha介绍 Jest Jest的特点: Jest的使用限制 Mocha Mocha的特点 使用Mocha的限制 Jest和Mocha的全面比较 我们应该使用哪个测试框架? 结论 什么是单元测试? 所谓单元测试,是对软…...

Oracle:merge into用法
文章目录 merge into使用场景merge into语法测试表普通模式 merge使用注意点 merge into MERGE 是 Oracle9i 新增的语法,根据源表对目标表进行匹配查询,匹配成功时更新,不成功时插入 比单独的 update insert 的方式效率要更高,尤…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
