二叉排序树(二叉查找树)
二叉排序树(二叉查找树)的性质:
- 若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值。
- 若它的右子树不为空,则右子树上所有结点的值均大于它的根将诶点的值。
- 它的左、右子树也分别为二叉排序树。
对二叉排序树进行中序遍历时,变可得到一个有序的序列。
构建二叉排序树不是为了排序,而是为了查找,也有利于插入和删除的实现。
代码
#include <stdio.h>
#include <string.h>
#include <stdbool.h>
#include <stdlib.h>typedef struct Node
{int data;struct Node *left, *right;
} Node;// returns true on success with ret set to found node.
// returns false on failure with ret set to last accessed node.
// parent passed is NULL at the first call.
bool
search_v2 (Node *tree, int key, Node *parent, Node **ret)
{if (tree == NULL){*ret = parent;return false;}if (key == tree->data){*ret = tree;return true;}else if (key < tree->data)return search_v2 (tree->left, key, tree, ret);elsereturn search_v2 (tree->right, key, tree, ret);}// Returns pointer to the searched node on success, or 0 on failure.
Node *
search (Node *tree, int key)
{if (tree == NULL)return NULL;if (key == tree->data)return tree;else if (key < tree->data)return search (tree->left, key);//search at left childelsereturn search (tree->right, key);//search at right child
}bool
insert_node (Node **ptree, int key)
{Node *result, *new_node;if (search_v2 (*ptree, key, NULL, &result) == false) //not found{new_node = malloc (sizeof (Node));*new_node = (Node){.data = key,.left = NULL,.right = NULL};if (result == NULL)*ptree = new_node; // insert as new rootelse if (key < result->data)result->left = new_node; //insert as lchildelseresult->right = new_node; //insert as rchildreturn true;}elsereturn false;//there is already such value, refuses to insert.
}bool
delete_node_impl (Node **ptree)
{Node *prev;if ( (*ptree)->right == NULL) //if right is NULL, reset it to its left child{prev = *ptree;*ptree = (*ptree)->left;free (prev);}else if ( (*ptree)->left == NULL) //if left is NULL, reset it to its right{prev = *ptree;*ptree = (*ptree)->right;free (prev);}else//both left and right are not NULL{prev = *ptree;Node *s = (*ptree)->left;while (s->right != NULL) //turn left, then turn to right for ever{prev = s;s = s->right;}//找到了左子树中的最大结点(直接前驱),这意味者它的right为NULL。(*ptree)->data = s->data;//s points to the direct predecessor of deleted nodeif (prev != *ptree) //如果直接前驱的父结点 != 被删除的treeprev->right = s->left; //reset right tree of prevelse //否则,说明tree的左子树没有右子树,直接替换左子树即可。prev->left = s->left; //reset left tree of prevfree (s);//释放被删除的结点——直接前驱。}return true;
}bool
delete_node (Node **ptree, int key)
{if (ptree == NULL)return false;else{if (key == (*ptree)->data)return delete_node_impl (ptree);else if (key < (*ptree)->data)return delete_node (& (*ptree)->left, key);elsereturn delete_node (& (*ptree)->right, key);}
}void
traverse_LDR (Node *tree)
{if (tree == NULL)return;traverse_LDR (tree->left);printf ("%d\n", tree->data);traverse_LDR (tree->right);
}int main (void)
{Node *tree = NULL;insert_node (&tree, 100);insert_node (&tree, 101);insert_node (&tree, 102);insert_node (&tree, 103);insert_node (&tree, 104);traverse_LDR (tree);}#include <stddef.h>
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
#include <stdbool.h>typedef struct Node
{int data;struct Node *left;struct Node *right;
} Node;Node *
create_tree()
{return NULL;
}enum search_result
{NOT_FOUND,};// 成功返回true,同时ret保留找到的结点。
// 失败返回false,同时ret保留最后一个结点(用于插入)。
// parent是辅助参数,第一次传入时应为NULL
bool
search_v2 (Node *tree, int key, Node *parent, Node **result)
{if (tree == NULL){*result = parent;return false;}if (tree->data == key){*result = tree;return true;}if (key < tree->data)return search_v2 (tree->left, key, tree, result);elsereturn search_v2 (tree->right, key, tree, result);
}Node *
search (Node *tree, int key)
{Node *result;if (search_v2 (tree, key, NULL, &result))return result;return NULL;
}bool
insert_node (Node **ptree, int key)
{Node *result;if (search_v2 (*ptree, key, NULL, &result) == false){Node *new_node = malloc (sizeof (Node));*new_node = (Node){.data = key,.left = NULL,.right = NULL};if (result == NULL) //说明树为空,插入为根结点*ptree = new_node;else if (key < result->data)result->left = new_node;elseresult->right = new_node;return true;}elsereturn false;// 已经存在相同值,插入失败
}bool
delete_node_impl (Node **ptree)
{Node *prev;if ( (*ptree)->right == NULL) // 只有左子树,重设左子树即可{prev = *ptree;*ptree = (*ptree)->left;free (prev);}else if ( (*ptree)->left == NULL) //只 有右子树,重设右子树即可{prev = *ptree;*ptree = (*ptree)->right;free (prev);}else// 都不为空{prev = *ptree;Node *predecessor = (*ptree)->left;while (predecessor->right != NULL){prev = predecessor;predecessor = predecessor->right;}(*ptree)->data = predecessor->data;if (*ptree != prev)prev->right = predecessor->left;else(*ptree)->left = predecessor->left;}return true;
}bool
delete_node (Node **ptree, int key)
{if (*ptree == NULL)return false;else{if ( (*ptree)->data == key)return delete_node_impl (ptree);else if (key < (*ptree)->data)return delete_node (& (*ptree)->left, key);elsereturn delete_node (& (*ptree)->right, key);}
}void
traverse_LDR (Node *tree)
{if (tree == NULL)return;traverse_LDR (tree->left);printf ("%d\n", tree->data);traverse_LDR (tree->right);
}int main (void)
{Node *tree = NULL;insert_node (&tree, 100);insert_node (&tree, 101);insert_node (&tree, 102);insert_node (&tree, 103);insert_node (&tree, 104);delete_node (&tree, 100);delete_node (&tree, 101);delete_node (&tree, 102);delete_node (&tree, 103);delete_node (&tree, 104);traverse_LDR (tree);}
经测试没有内存泄露。
参考书籍:大话数据结构
相关文章:
)
二叉排序树(二叉查找树)
二叉排序树(二叉查找树)的性质: 若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值。若它的右子树不为空,则右子树上所有结点的值均大于它的根将诶点的值。它的左、右子树也分别为二叉排序树。 对二叉…...

Python简单应用VII
题目 编程实现下述各题。 1.使用异常处理结构捕获多种可能的异常,如列表下标索引越界异常(IndexError)、试 图访问一个系统对象没有的属性所发生的异常(AttributeError)、读一个文件但该文件不存在。 2. 新建并打开文件stud1.txt,如果文件已存在就提示“…...
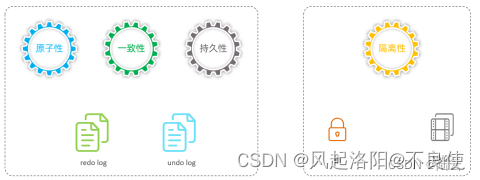
mysql--InnoDB存储引擎--架构和事务
MySQL进阶篇 文章目录 架构1、逻辑结构InnoDB 逻辑存储单元主层级关系图:1、表空间2、段3、区4、页5、行总结: 2、架构2、1 内存架构2、2 磁盘架构 3、事务3、1事务基础(1)事务(2)特性 架构 1、逻辑结构 I…...
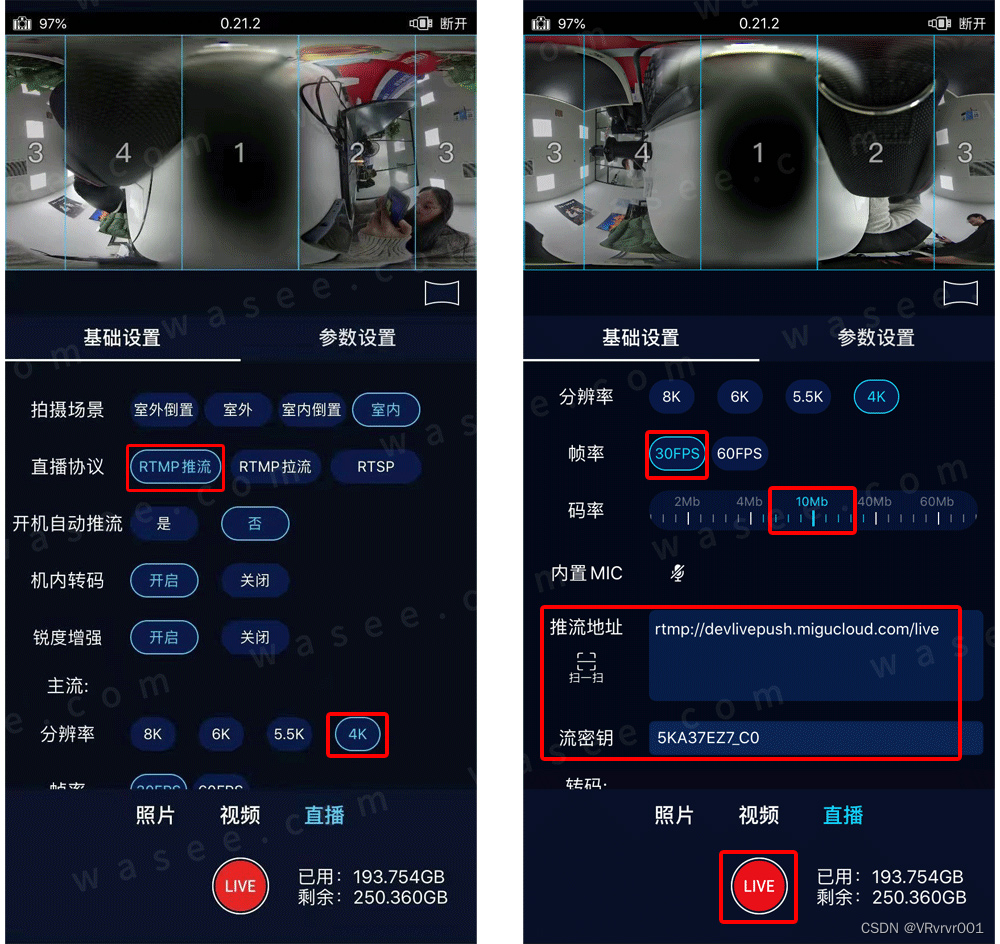
0基础学习VR全景平台篇 第79篇:全景相机-泰科易如何直播推流
泰科易科技是中国的一家研发全景相机的高科技公司,前不久,在2020世界VR产业大会上发布了新一代5G VR直播影像采集终端--360starlight。以其出色的夜景成像效果和一“部”到位的直播方案重新定义了VR慢直播相机,对行业具有高度借鉴意义。 本文…...

代码调试4:实现退化模型的训练
代码调试:实现退化模型的训练 作者:安静到无声 个人主页 目录 代码调试:实现退化模型的训练问题1:如何在coco原始编码的基础上修改原始的文件?**方法1**:修改生成的文件**方法2**:直接修改源文件`instances_train2014.json`和`instances_val2014.json`问题2:构建退化后…...
8.7工作总结
一、我们想自定义一个titileBar出现如下这种情况,发现他原来的titileBar还未隐藏。 后来我尝试修改主题使得他没有主题noActionBar发现也不行,后来我参考原先我看过的项目使用了如下代码 this.getActionBar().hide();发现会报这个错误java.lang.NullPoi…...

数据库的约束 详解
一、约束的概述 1.概念:约束是作用于表中字段上的规则,用于限制存储在表中的数据。 2.目的:保证数据库中数据的正确、有效性和完整性。 3.分类: 约束描述关键字非空约束限制该字段的数据不能为nullNOT NULL唯一约束保证该字段的所有数据都是唯一、不…...

Tomcat 编程式启动 JMX 监控
通过这篇文章,我们可以了解到,利用 JMX 技术可以方便获取 Tomcat 监控情况。但是我们采用自研的框架而非大家常见的 SpringBoot,于是就不能方便地通过设置配置开启 Tomcat 的 JMX,——尽管我们也是基于 Tomcat 的 Web 容器&#x…...
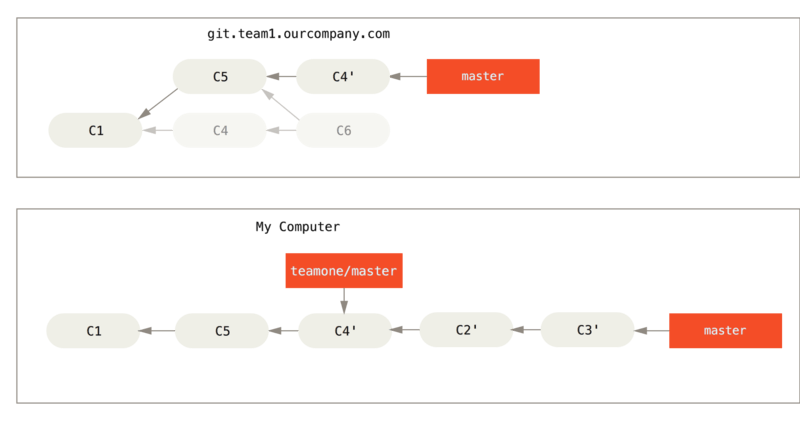
Git rebase和merge区别详解
文章目录 变基的基础用法变基过程中的冲突解决冲突后无法push问题更新变基后的代码更有趣的变基用法变基的风险用变基解决变基变基 vs 合并 此文在阅读前需要有一定的git命令基础,若基础尚未掌握,建议先阅读这篇文章Git命令播报详版 在 Git 中整合来自不…...

JDK动态代理的原理解析、代码实现
代理就像是:买家(客户端)——销售(代理对象)——工厂(目标) 买家不用直接去工厂买,而是直接通过销售就可以购买到,假设工厂生产的是杯子,那么工厂只需要提供杯子,而销售在不改变杯子的生产过程的情况下对杯子进行包装设…...

理解和使用Ansible模块,简化自动化任务
Ansible是一款强大的自动化工具,用于管理和配置IT基础设施。在Ansible的世界中,模块(Module)是至关重要的组成部分。本文将深入探讨Ansible模块,了解它们如何简化自动化任务的执行过程。 Ansible模块是Ansible的核心组…...
Docker 快速安装 MinIO
概述 MinIO 是一款基于Go语言的高性能对象存储服务,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等。 拉取docker镜像 docker pull minio/minio创建宿主机数据目录(共享数据卷) 此…...
【源码分析】Nacos如何使用AP协议完成服务端之间的数据同步?
AP节点的同步使用的是异步任务消息队列的方式来实现的。 取出任务之后将会放入到一个List集合中。 然后会发现任务的执行是由条件的。 首先是当前集群的节点数量等于1000,那么此时会直接开始同步,当然这个条件在小项目中不会成立,所以还有…...

黑客删除服务器数据后,间谍软件制造商 LetMeSpy 关闭
总部位于波兰的间谍软件 LetMeSpy 已不再运行,并表示将在 6 月份的一次数据泄露事件中关闭其服务器,其中包括从数千名受害者手机中窃取的大量数据。 LetMeSpy 在其网站上以英语和波兰语发布的通知中确认该间谍软件服务已“永久关闭”,并将于 …...

ebay儿童书包产品CPC认证
儿童书包是一种能够盛放书本或者文具的包。现在的书包五花八门,以普通的布料或者是帆布等制成,有背带,包内一般分栏。一般分三种,背在身后的,挎在肩上的,轮式(可以拖行)的。 一、美国…...

Debezium系列之:增量快照初始化历史数据实际应用案例
Debezium系列之:增量快照初始化历史数据实际应用案例 一、需求背景二、查看数据库表数据三、使用增量快照采集历史数据四、初始化历史数据一、需求背景 采集数据库数据发送到Kafka Topic,供下游实时开发消费,在采集最新数据的同时,希望把历史数据也发送到Kafka Topic同时采…...

Transformer1.0-预热
一.Encoder encoder:译为编码器,负责将输入序列压缩成指定长度的向量,这个向量就可以堪称是这个序列的语义。然后可进行编码或特征提取等操作 在transformer中encoder由6个相同的层组成,每个层包含 Multi-Head Self-AttentionPosition-Wise …...

【探索Linux】—— 强大的命令行工具 P.2(Linux下基本指令)
前言 前面我们讲了C语言的基础知识,也了解了一些数据结构,并且讲了有关C的一些知识,也相信大家都掌握的不错,今天博主将会新开一个Linux专题,带领大家继续学习有关Linux的内容。今天第一篇文章博主首先带领大家了解一下…...

供应链售后服务自动化,利用软件机器人将数据整合提升效率
随着供应链管理的不断发展,售后服务的重要性也日益凸显。良好的售后服务不仅可以提高客户满意度,还能增强品牌形象和忠诚度。然而,传统的供应链售后服务往往存在繁琐的操作、低效率和易出错的问题。为了解决这一挑战,越来越多的企…...

VIM浅谈
VIM 1. 文件1.1 管理多个文件 仅以此篇纪念VIM作者Bram Moolenaar。 1. 文件 刚刚使用VIM,很多小伙伴疑惑的就是如何退出VIM,一顿乱按结果修改了文件,q又退不出去,还需要保存。这是因为文件是保存在磁盘里的,使用Vim…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...

JS的传统写法 vs 简写形式
一、条件判断与逻辑操作 三元运算符简化条件判断 // 传统写法 let result; if (someCondition) {result yes; } else {result no; }// 简写方式 const result someCondition ? yes : no;短路求值 // 传统写法 if (condition) {doSomething(); }// 简写方式 condition &…...
