因果推断(三)双重差分法(DID)
因果推断(三)双重差分法(DID)
双重差分法是很简单的群体效应估计方法,只需要将样本数据随机分成两组,对其中一组进行干预。在一定程度上减轻了选择偏差带来的影响。
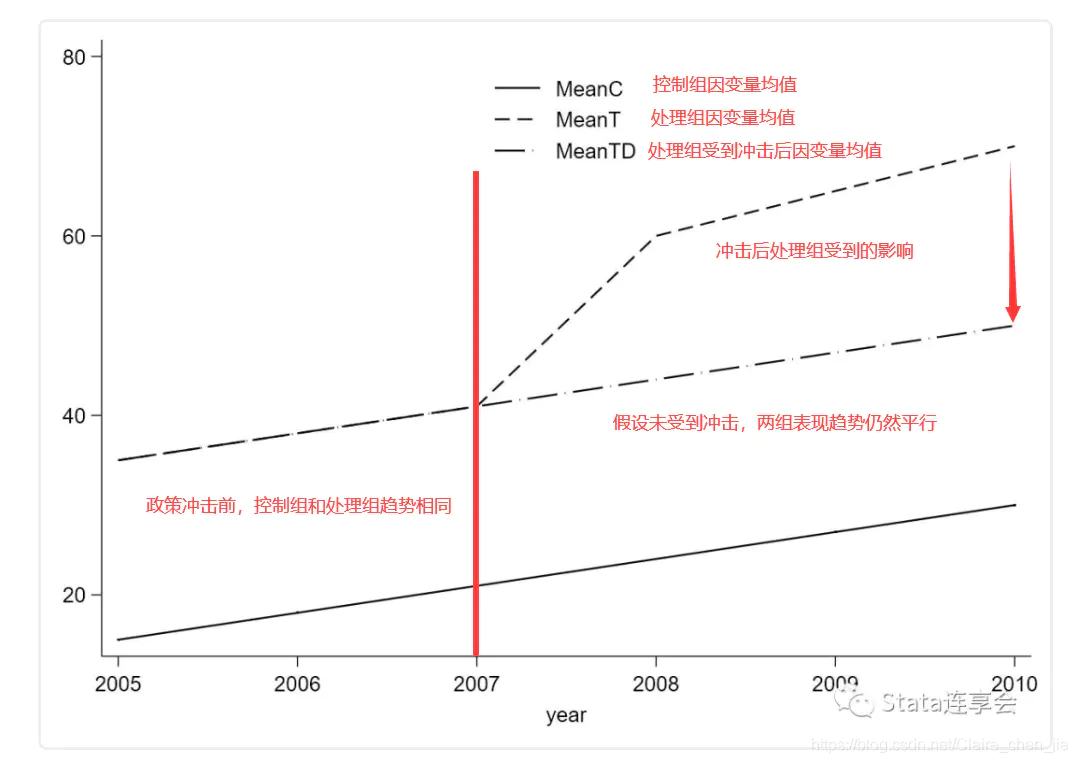
因果效应计算:对照组y在干预前后的均值差( A ˉ 2 − A ˉ 1 \bar A_2 - \bar A_1 Aˉ2−Aˉ1),实验组y在干预前后的均值差( B ˉ 2 − B ˉ 1 \bar B_2 - \bar B_1 Bˉ2−Bˉ1),则因果效应: ( B ˉ 2 − B ˉ 1 ) − ( A ˉ 2 − A ˉ 1 ) (\bar B_2 - \bar B_1)-(\bar A_2 - \bar A_1) (Bˉ2−Bˉ1)−(Aˉ2−Aˉ1)
假设前提:DID有一个很重要且很严格的平行趋势假设,即实验组和对照组在没有干预的情况下,结果的趋势是一样的。
准备数据
from faker import Faker
from faker.providers import BaseProvider, internet
from random import randint
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import statsmodels.formula.api as smf
import warningswarnings.filterwarnings('ignore')# 绘图初始化
%matplotlib inline
sns.set(style="ticks")
# 自定义数据
fake = Faker('zh_CN')
class MyProvider(BaseProvider):def myCityLevel(self):cl = ["一线", "二线", "三线", "四线+"]return cl[randint(0, len(cl) - 1)]def myGender(self):g = ['F', 'M']return g[randint(0, len(g) - 1)]
fake.add_provider(MyProvider)# 构造假数据,模拟用户特征
uid=[]
cityLevel=[]
gender=[]
for i in range(10000):uid.append(i+1)cityLevel.append(fake.myCityLevel())gender.append(fake.myGender())raw_data= pd.DataFrame({'uid':uid,'cityLevel':cityLevel,'gender':gender,})raw_data['class'] = raw_data['uid'].map(lambda x: 'A' if x % 2 == 1 else 'B') # 按奇偶随机分组# 构造did数据
df = pd.DataFrame(columns=['uid','cityLevel','gender', 'class', 'sales', 'dt'])
for i,j in enumerate(range(2005,2011)):lift = 1+i*0.05df_temp = raw_data.copy()df_temp['sales'] = [int(x) for x in np.random.normal(300*lift, 60*lift, df_temp.shape[0])]df_temp['sales'] = df_temp.apply(lambda x: x.sales*0.88 if x['class']=='A' else x.sales, axis=1)if j>2007:df_temp['sales'] = df_temp.apply(lambda x: x.sales*(1+i*0.02) if x['class']=='B' else x.sales, axis=1)df_temp['dt'] = jdf=pd.concat([df,df_temp])df_did = df.groupby(['class', 'dt'])['sales'].sum().reset_index()
验证平行趋势假设
# 计算文字的y坐标
y_text = df_did.query('dt == 2007 and `class`=="B"')['sales'].values[0]
# 绘图查看干预前趋势
fig, ax = plt.subplots(figsize=(12,8))
sns.lineplot(x="dt", y="sales", hue="class", data=df_did)
ax.axvline(2007, color='r', linestyle="--", alpha=0.8)
plt.text(2007, y_text, 'treatment')
plt.show()
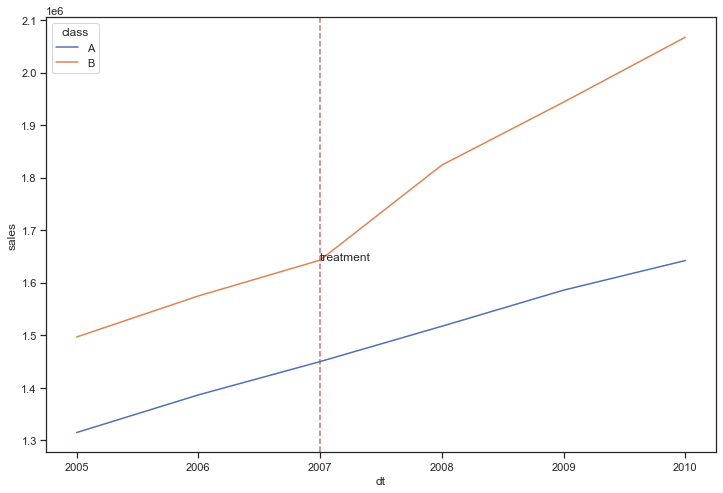
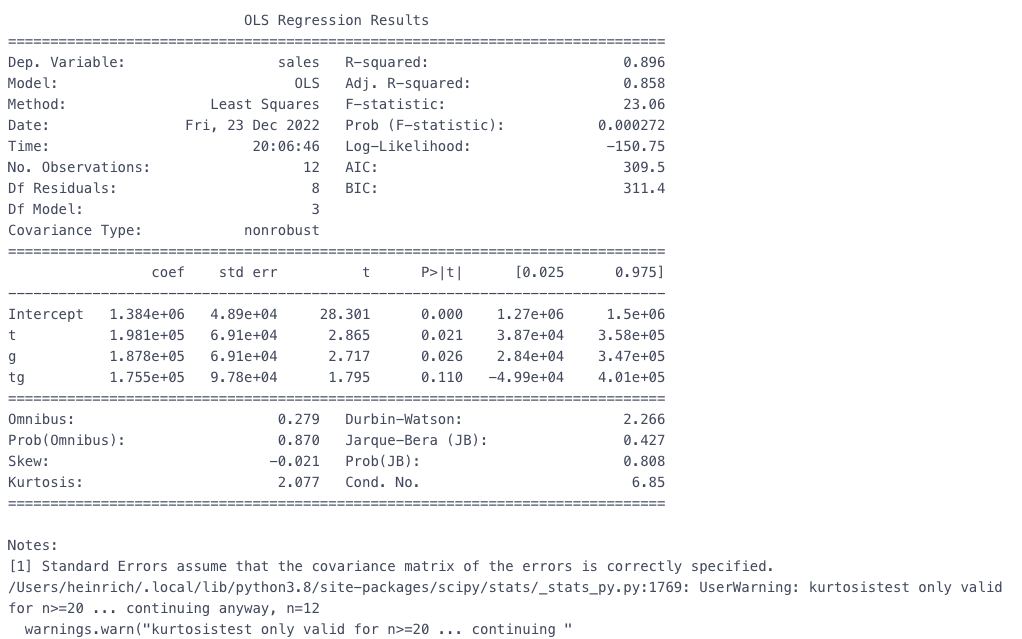
除了画图观察平行趋势,也可以通过回归拟合,参考自如何使用Python计算双重差分模型
# 方法2 回归计算 df_did['t'] = df_did['treatment'].map(lambda x: 1 if x=='干预后' else 0) # 是否干预后 df_did['g'] = df_did['class'].map(lambda x: 1 if x=='B' else 0) # 是否试验组 df_did['tg'] = df_did['t']*df_did['g'] # 交互项# 回归 est = smf.ols(formula='sales ~ t + g + tg', data=df_did).fit() print(est.summary())
可以看到交互项tg并不显著,因此可以认为具备平行趋势
计算因果效应
# 计算因果效应
df_did['treatment'] = df_did['dt'].map(lambda x: '干预后' if x>2007 else '干预前')
df_did_cal = df_did.groupby(['class', 'treatment'])['sales'].mean()
did = (df_did_cal.loc['B', '干预后'] - df_did_cal.loc['B', '干预前']) - \(df_did_cal.loc['A', '干预后'] - df_did_cal.loc['A', '干预前'])
print(did)
175541.82000000007
总结
在实际业务中,平行趋势假设是很难满足的,因此常常会先进性PSM构造相似的样本,这样两组群体基本上就会符合平行趋势假设了,所以常见以PSM+DID进行因果推断,有兴趣的同学可以结合这两期的内容自行尝试。
共勉~
相关文章:
因果推断(三)双重差分法(DID)
因果推断(三)双重差分法(DID) 双重差分法是很简单的群体效应估计方法,只需要将样本数据随机分成两组,对其中一组进行干预。在一定程度上减轻了选择偏差带来的影响。 因果效应计算:对照组y在干预…...
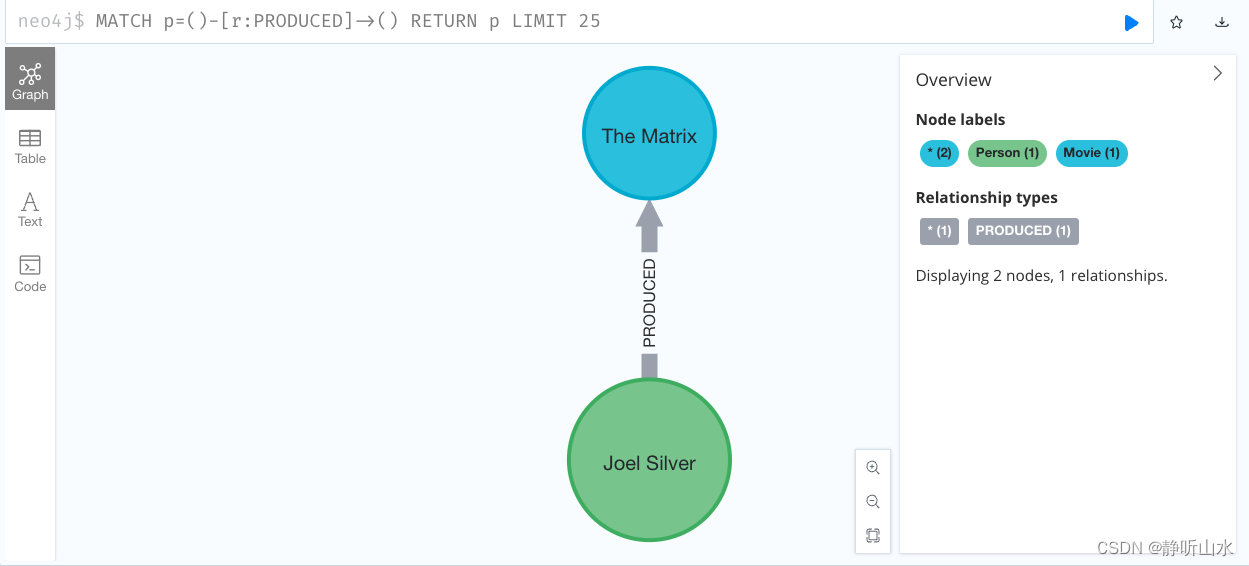
neo4j入门实例介绍
使用Cypher查询语言创建了一个图数据库,其中包含了电影《The Matrix》和演员Keanu Reeves、Carrie-Anne Moss、Laurence Fishburne、Hugo Weaving以及导演Lilly Wachowski和Lana Wachowski之间的关系。 CREATE (TheMatrix:Movie {title:The Matrix, released:1999,…...

CGAL-2D和3D线性几何内核-点和向量-内核扩展
文章目录 1.介绍1.1.鲁棒性 2.内核表示2.1.通过参数化实现泛型2.2.笛卡尔核2.3.同质核2.4.命名约定2.5.内核作为trait类2.6.选择内核和预定义内核 3.几何内核3.1.点与向量3.2.内核对象3.3.方位和相对位置 4.谓语和结构4.1.谓词4.2.结构4.3.交集和变量返回类型4.4.例子4.5.构造性…...

Ubuntu 22.04 安装docker
参考: https://docs.docker.com/engine/install/ubuntu/ 支持的Ubuntu版本: Ubuntu Lunar 23.04Ubuntu Kinetic 22.10Ubuntu Jammy 22.04 (LTS)Ubuntu Focal 20.04 (LTS) 1 卸载旧版本 非官方的安装包,需要先卸载: docker.io…...

电脑维护进阶:让你的“战友”更强大、更持久!
前言 无论是学习还是工作,电脑已经成为了IT人必不可少的得力助手。然而,电脑的性能和寿命需要经过细心的维护来保证。本文将详细探讨如何维护你的电脑,延长它的寿命,以及一些实用建议。 硬件保养篇 内部清洁 灰尘会导致电脑散热…...

【Leetcode】75.颜色分类
一、题目 1、题目描述 给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。 我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。 必须在不使用库内置的 sort 函数的情况下解决这个问…...

Pytesseract学习笔记
函数 pytesseract.image_to_string(image: Any, lang: Any None, …) 识别图像中的文本。 Parameters image(Any):输入图像,不接受bytes类型。...
cnvd通用型证书获取姿势
因为技术有限,只能挖挖不用脑子的漏洞,平时工作摸鱼的时候通过谷歌引擎引擎搜索找找有没有大点的公司有sql注入漏洞,找的方法就很简单,网站结尾加上’,有异常就测试看看,没有马上下一家,效率至上…...

elasticsearch的副本和分片的区别
es/elasticsearch的副本和分片的区别 一:概念 (1)集群(Cluster): ES可以作为一个独立的单个搜索服务器。不过,为了处理大型数据集,实现容错和高可用性,ES可以运行在许多互…...

Docker部署Gitlab
Docker部署Gitlab 文章目录 Docker部署Gitlab前置环境部署步骤初始化配置文件80端口部署方式(二选一)非80端口需要的部署方式(二选一)修改 gitlab.rb修改 gitlab.yml刷新配置 前置环境 docker 19.03.13 es 7.2.0 部署步骤 初始…...

ABeam News | ABeam大中华区新人入社式,开启崭新的职场探索之旅吧!
ABeam News | ABeam大中华区新人入社式,开启崭新的职场探索之旅吧! 隔空投送 很高兴认识你 7月3日,FY24 ABeam大中华区新人入社式在西安隆重举办,ABeam大中华区董事长兼总经理中野洋辅先生专程莅临入社式现场,与89名…...

【C++】开源:sqlite3数据库配置使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍sqlite3数据库配置使用。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下…...
[Docker实现测试部署CI/CD----Jenkins集成相关服务器(3)]
目录 7、 Jenkins 集成 SonarQubeJenkins 中安装 SonarScanner下载移动修改配置文件 8、Jenkins配置SonarQube安装插件添加SonarQube添加 SonarScanner 9、Jenkins集成目标服务器 7、 Jenkins 集成 SonarQube Jenkins 中安装 SonarScanner SonarScanner 是一种代码扫描工具&am…...
【Shell】基础语法(二)
文章目录 一、Shell基本语法文件名代换命令代换算术代换转义字符引号 二、Shell脚本语法条件测试分支结构循环 三、总结 一、Shell基本语法 文件名代换 用于匹配的字符称为通配符(Wildcard),如:* ? [ ] 具体如下: *…...
Unity之webgl端通过vue3接入腾讯云联络中心SDK
腾讯云联络中心SDK:云联络中心 Web-SDK 开发指南-文档中心-腾讯云 (tencent.com) 1 首先下载Demo 1.1 对其进行解压 1.2根据文档操作 查看README.md,根据说明设置server下的dev.js里的相关参数。 然后打开电脑终端,cd到项目的路径: 安装…...

《算法竞赛·快冲300题》每日一题:“连接草坪(II)”
《算法竞赛快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。 所有题目放在自建的OJ New Online Judge。 用C/C、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。 文章目录 题目描述题解C代码Java代码Python代码 “ 连…...
LNMP及论坛搭建(第一个访问,单节点)
LNMP:目前成熟的一个企业网站的应用模式之一,指的是一套协同工作的系统和相关软件 能够提供静态页面服务,也可以提供动态web服务,LNMP是缩写 L:指的是Linux操作系统。 N:指的是nginx,nginx提…...
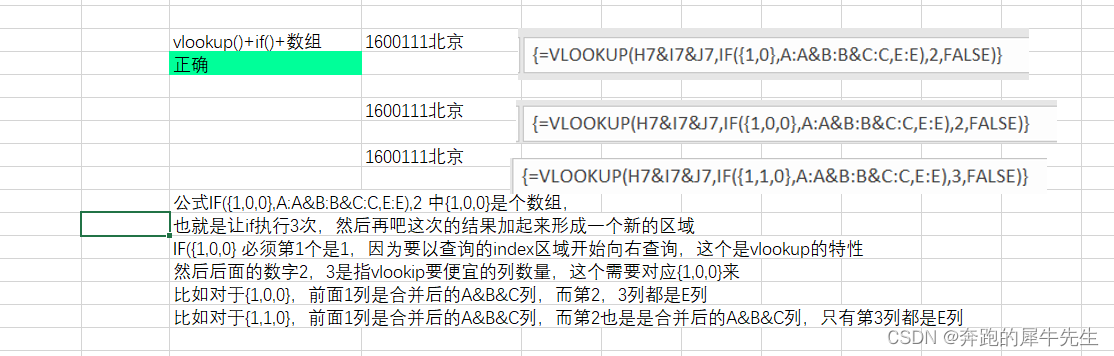
EXCEL,多条件查询数字/文本内容的4种方法
目录 1 问题:如何根据多条件查询到想要的内容 2 方法总结 2.1 方法1: sumif() 和sumifs() 适合查找符合条件的多个数值之和 2.2 方法2:使用lookup(1,0/((区域1条件1)*(区域2条件2)*....),结果查询区域) 2.3 方法3:使用 ind…...

全志D1-H (MQ-Pro)驱动 OV5640 摄像头
内核配置 运行 m kernel_menuconfig 勾选下列驱动 Device Drivers ---><*> Multimedia support --->[*] V4L platform devices ---><*> Video Multiplexer[*] SUNXI platform devices ---><*> sunxi video input (camera csi/mipi…...

2023下半年软考初级网络管理员报名入口-报名流程-备考方法
软考初级网络管理员2023下半年考试时间: 2023年下半年软考初级网络管理员的考试时间为11月4日、5日。考试时间在全国各地一致,建议考生提前备考。共分两科,第一科基础知识考试具体时间为9:00到11:30;第二科应用技术考试具体时间为…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
