Pytorch Tutorial【Chapter 2. Autograd】
Pytorch Tutorial
文章目录
- Pytorch Tutorial
- Chapter 2. Autograd
- 1. Review Matrix Calculus
- 1.1 Definition向量对向量求导
- 1.2 Definition标量对向量求导
- 1.3 Definition标量对矩阵求导
- 2.关于autograd的说明
- 3. grad的计算
- 3.1 Manual手动计算
- 3.2 backward()自动计算
- Reference
Chapter 2. Autograd
1. Review Matrix Calculus
1.1 Definition向量对向量求导
Define the derivative of a function mapping f : R n → R m f:\mathbb{R}^n\to\mathbb{R}^m f:Rn→Rm as the n × m n\times m n×m matrix of partial derivatives. That is, if x ∈ R n , f ( x ) ∈ R m x\in\mathbb{R}^n,f(x)\in\mathbb{R}^m x∈Rn,f(x)∈Rm, the derivative of f f f with respect to x x x is defined as
[ ∂ f ∂ x ] i j = ∂ f i ∂ x i \begin{bmatrix} \frac{\partial f}{\partial x} \end{bmatrix}_{ij} = \frac{\partial f_i}{\partial x_i} [∂x∂f]ij=∂xi∂fi
Let
x = [ x 1 x 2 ⋮ x n ] , f ( x ) = [ f 1 ( x ) f 2 ( x ) ⋮ f m ( x ) ] x = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}, f(x) = \begin{bmatrix} f_1(x) \\ f_2(x) \\ \vdots \\ f_m(x) \end{bmatrix} x= x1x2⋮xn ,f(x)= f1(x)f2(x)⋮fm(x)
then we define the Jacobian Matrix
∂ f ∂ x = [ ∂ f 1 ∂ x 1 ∂ f 2 ∂ x 1 ⋯ ∂ f m ∂ x 1 ∂ f 1 ∂ x 2 ∂ f 2 ∂ x 2 ⋯ ∂ f m ∂ x 2 ⋮ ⋮ ⋱ ⋮ ∂ f 1 ∂ x n ∂ f 2 ∂ x n ⋯ ∂ f m ∂ x n ] \frac{\partial f}{\partial x} = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_2}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_1} \\ \frac{\partial f_1}{\partial x_2} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_2} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_1}{\partial x_n} & \frac{\partial f_2}{\partial x_n} & \cdots & \frac{\partial f_m}{\partial x_n} \\ \end{bmatrix} ∂x∂f= ∂x1∂f1∂x2∂f1⋮∂xn∂f1∂x1∂f2∂x2∂f2⋮∂xn∂f2⋯⋯⋱⋯∂x1∂fm∂x2∂fm⋮∂xn∂fm
1.2 Definition标量对向量求导
If f f f is scalar, one has
∂ f ∂ x = [ ∂ f ∂ x 1 ∂ f ∂ x 2 ⋮ ∂ f ∂ x n ] \frac{\partial f}{\partial x} = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n} \\ \end{bmatrix} ∂x∂f= ∂x1∂f∂x2∂f⋮∂xn∂f
这其实是一种分母布局
1.3 Definition标量对矩阵求导
Now we give some results on the derivative of scalar functions of a matrix. Let X = [ x i j ] X=[x_{ij}] X=[xij] be a matrix of order m × n m\times n m×n and let y = f ( X ) y=f(X) y=f(X) be a scalar function of X X X. The derivative of y y y with respect to X X X, denoted by ∂ y ∂ X \frac{\partial y}{\partial X} ∂X∂y, is defined as the following matrix of order m × n m\times n m×n,
G = ∂ y ∂ X = [ ∂ y ∂ x 11 ∂ y ∂ x 12 ⋯ ∂ y ∂ x 1 n ∂ y ∂ x 21 ∂ y ∂ x 22 ⋯ ∂ y ∂ x 2 n ⋮ ⋮ ⋱ ⋮ ∂ y ∂ x m 1 ∂ y ∂ x m 2 ⋯ ∂ y ∂ x m n ] = [ ∂ y ∂ x i j ] G = \frac{\partial y}{\partial X} = \begin{bmatrix} \frac{\partial y}{\partial x_{11}} & \frac{\partial y}{\partial x_{12}} & \cdots & \frac{\partial y}{\partial x_{1n}} \\ \frac{\partial y}{\partial x_{21}} & \frac{\partial y}{\partial x_{22}} & \cdots & \frac{\partial y}{\partial x_{2n}} \\ \vdots & \vdots & \ddots & \vdots& \\ \frac{\partial y}{\partial x_{m1}} & \frac{\partial y}{\partial x_{m2}} & \cdots & \frac{\partial y}{\partial x_{mn}} \end{bmatrix} = \Big[\frac{\partial y}{\partial x_{ij}} \Big] G=∂X∂y= ∂x11∂y∂x21∂y⋮∂xm1∂y∂x12∂y∂x22∂y⋮∂xm2∂y⋯⋯⋱⋯∂x1n∂y∂x2n∂y⋮∂xmn∂y =[∂xij∂y]
2.关于autograd的说明
torch.Tensor 是包的核心类。如果将其属性 tensor.requires_grad 设置为 True,则会开始跟踪针对 tensor 的所有操作。完成计算后,您可以调用 tensor.backward() 来自动计算所有梯度。该张量的梯度将累积到 tensor.grad 属性中。
要停止 tensor 历史记录的跟踪,您可以调用 tensor.detach(),它将其与计算历史记录分离,并防止将来的计算被跟踪。
要停止跟踪历史记录(和使用内存),您还可以将代码块使用 with torch.no_grad(): 包装起来。在评估模型时,这是特别有用,因为模型在训练阶段具有 requires_grad = True 的可训练参数有利于调参,但在评估阶段我们不需要梯度。
还有一个类对于 autograd 实现非常重要那就是 Function。Tensor 和 Function 互相连接并构建一个非循环图,它保存整个完整的计算过程的历史信息。每个张量都有一个 tensor.grad_fn 属性保存着创建了张量的 Function 的引用,(如果用户自己创建张量,则 grad_fn=None)。
如果你想计算导数,你可以调用 tensor.backward()。如果 Tensor 是标量(即它包含一个元素数据),则不需要指定任何参数backward(),但是如果它有更多元素,则需要指定一个gradient 参数来指定张量的形状。
最后的计算结果保存在tensor.grad属性里
- 使用
tensor.requires_grad在初始化时,设置跟踪梯度
import torch
import numpy as np
x = torch.ones(2,2, requires_grad=True)
print(x)
结果如下
tensor([[1., 1.],[1., 1.]], requires_grad=True)
- 设置了跟踪梯度的tensor,将会出现
tensor.grad_fn的属性,用于记录上次计算的Function
y = torch.add(x, 1)
print(y)
print(y.grad_fn)
结果如下
tensor([[2., 2.],[2., 2.]], grad_fn=<AddBackward0>)
<AddBackward0 object at 0x0000020D723EBE80>
tensor.requires_grad_(True / False)会改变张量的 requires_grad 标记。 如果没有提供相应的参数输入的标记默认为 False。
a = torch.randn(2,2)
a = (a * 3) / (a-1)
print(a)
a.requires_grad_(True)
print(a)
a = a + 1
print(a)
tensor([[ 0.0646, -46.3478],[ 5.6683, -0.8896]])
tensor([[ 0.0646, -46.3478],[ 5.6683, -0.8896]], requires_grad=True)
tensor([[ 1.0646, -45.3478],[ 6.6683, 0.1104]], grad_fn=<AddBackward0>)
3. grad的计算
3.1 Manual手动计算
- 可以使用函数
torch.autograd.grad()来手动计算梯度,详细可参考此处

例如计算 y = x 1 2 + x 2 2 + x 1 x 2 y = x_1^2 + x_2^2 + x_1x_2 y=x12+x22+x1x2的梯度
x1 = torch.tensor(3., requires_grad=True)
x2 = torch.tensor(1., requires_grad=True)
y = x1**2+x2**2+x1*x2# 求一阶导数
# torch.autograd.grad(y, x1,retain_graph=True, create_graph=True)
x1_1 = torch.autograd.grad(y, x1, retain_graph=True, create_graph=True)[0]
x2_1 = torch.autograd.grad(y, x2, retain_graph=True, create_graph=True)[0]
print(x1_1,x2_1)# 求二阶混合偏导数
x1_11 = torch.autograd.grad(x1_1, x1)[0]
x1_12 = torch.autograd.grad(x1_1, x2)[0]
x2_21 = torch.autograd.grad(x2_1, x1)[0]
x2_22 = torch.autograd.grad(x2_1, x2)[0]
print(x1_11,x1_12,x2_21,x2_22)
结果如下
tensor(7., grad_fn=<AddBackward0>) tensor(5., grad_fn=<AddBackward0>)
tensor(2.) tensor(1.) tensor(1.) tensor(2.)
3.2 backward()自动计算
当输出是标量scalar函数时
考虑如下的计算问题
x = torch.ones(2,2, requires_grad=True)
y = x + 2
print(y)
z = y * y * 3
out = z.mean()
print(z, out) #输出out是一个标量
out.backward()
print(x.grad)
输出是
tensor([[3., 3.],[3., 3.]], grad_fn=<AddBackward0>)
tensor([[27., 27.],[27., 27.]], grad_fn=<MulBackward0>) tensor(27., grad_fn=<MeanBackward0>)
tensor([[4.5000, 4.5000],[4.5000, 4.5000]])
X = [ x 1 x 2 x 3 x 4 ] = [ 1 1 1 1 ] X =\begin{bmatrix} x_1 & x_2 \\ x_3 & x_4 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} X=[x1x3x2x4]=[1111]
中间变量是
Z = [ z 1 z 2 z 3 z 4 ] = [ 3 ( x 1 + 2 ) 2 3 ( x 1 + 2 ) 2 3 ( x 1 + 2 ) 2 3 ( x 1 + 2 ) 2 ] Z =\begin{bmatrix} z_1 & z_2 \\ z_3 & z_4 \end{bmatrix} = \begin{bmatrix} 3(x_1+2)^2 & 3(x_1+2)^2 \\ 3(x_1+2)^2 & 3(x_1+2)^2 \end{bmatrix} Z=[z1z3z2z4]=[3(x1+2)23(x1+2)23(x1+2)23(x1+2)2]
最后获得是输出是
out = 1 4 ∑ i = 1 z i = 1 4 ( z 1 + z 2 + z 3 + z 4 ) = 1 4 ( 3 ( x 1 + 2 ) 2 + 3 ( x 2 + 2 ) 2 + 3 ( x 3 + 2 ) 2 + 3 ( x 4 + 2 ) 2 ) = f ( x ) \begin{aligned} \text{out} & = \frac{1}{4}\sum_{i=1} z_i = \frac{1}{4}(z_1+z_2+z_3+z_4) \\ & = \frac{1}{4}(3(x_1+2)^2+3(x_2+2)^2+3(x_3+2)^2+3(x_4+2)^2) \\ & = f(\mathrm{x}) \end{aligned} out=41i=1∑zi=41(z1+z2+z3+z4)=41(3(x1+2)2+3(x2+2)2+3(x3+2)2+3(x4+2)2)=f(x)
其中将矩阵 X X X和矩阵 Z Z Z中的所有元素拼接为向量
x = [ x 1 , x 2 , x 3 , x 4 ] T z = [ z 1 , z 2 , z 3 , z 4 ] T \mathrm{x} = [x_1,x_2,x_3,x_4]^T \\ \mathrm{z} = [z_1,z_2,z_3,z_4]^T x=[x1,x2,x3,x4]Tz=[z1,z2,z3,z4]T
我们利用矩阵求导的链式法则
∂ f ∂ x = f ( x ) ∂ x = ∂ z ∂ x ∂ f ( x ) ∂ z \frac{\partial f}{\partial \mathrm{x}} = \frac{f(\mathrm{x})}{\partial \mathrm{x}} = \frac{\partial \mathrm{z}}{\partial \mathrm{x}} \frac{\partial f(\mathrm{x})}{\partial \mathrm{z}} ∂x∂f=∂xf(x)=∂x∂z∂z∂f(x)
再利用标量函数对矩阵导数的定义,则有
∂ f ∂ x = [ ∂ z 1 ∂ x 1 ∂ z 2 ∂ x 1 ∂ z 3 ∂ x 1 ∂ z 4 ∂ x 1 ∂ z 1 ∂ x 2 ∂ z 2 ∂ x 2 ∂ z 3 ∂ x 2 ∂ z 4 ∂ x 2 ∂ z 1 ∂ x 3 ∂ z 2 ∂ x 3 ∂ z 3 ∂ x 3 ∂ z 4 ∂ x 3 ∂ z 1 ∂ x 4 ∂ z 2 ∂ x 4 ∂ z 3 ∂ x 4 ∂ z 4 ∂ x 4 ] [ ∂ f ∂ z 1 ∂ f ∂ z 2 ∂ f ∂ z 3 ∂ f ∂ z 4 ] = [ 6 ( x 1 + 2 ) 0 0 0 0 6 ( x 2 + 2 ) 0 0 0 0 6 ( x 3 + 2 ) 0 0 0 0 6 ( x 4 + 2 ) ] [ 1 4 1 4 1 4 1 4 ] = [ 4.5 4.5 4.5 4.5 ] \frac{\partial f}{\partial \mathrm{x}} = \begin{bmatrix} \frac{\partial z_1}{\partial x_1} & \frac{\partial z_2}{\partial x_1} & \frac{\partial z_3}{\partial x_1} & \frac{\partial z_4}{\partial x_1} \\ \frac{\partial z_1}{\partial x_2} & \frac{\partial z_2}{\partial x_2} & \frac{\partial z_3}{\partial x_2} & \frac{\partial z_4}{\partial x_2} \\ \frac{\partial z_1}{\partial x_3} & \frac{\partial z_2}{\partial x_3} & \frac{\partial z_3}{\partial x_3} & \frac{\partial z_4}{\partial x_3} \\ \frac{\partial z_1}{\partial x_4} & \frac{\partial z_2}{\partial x_4} & \frac{\partial z_3}{\partial x_4} & \frac{\partial z_4}{\partial x_4} \end{bmatrix} \begin{bmatrix} \frac{\partial f}{\partial z_1} \\ \frac{\partial f}{\partial z_2} \\ \frac{\partial f}{\partial z_3} \\ \frac{\partial f}{\partial z_4} \end{bmatrix}= \begin{bmatrix} 6(x_1+2) & 0 & 0 & 0 \\ 0 & 6(x_2+2) & 0 & 0 \\ 0 & 0 & 6(x_3+2) & 0 \\ 0 & 0 & 0 & 6(x_4+2) \end{bmatrix} \begin{bmatrix} \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \end{bmatrix} = \begin{bmatrix} 4.5 \\ 4.5 \\ 4.5 \\ 4.5 \\ \end{bmatrix} ∂x∂f= ∂x1∂z1∂x2∂z1∂x3∂z1∂x4∂z1∂x1∂z2∂x2∂z2∂x3∂z2∂x4∂z2∂x1∂z3∂x2∂z3∂x3∂z3∂x4∂z3∂x1∂z4∂x2∂z4∂x3∂z4∂x4∂z4 ∂z1∂f∂z2∂f∂z3∂f∂z4∂f = 6(x1+2)00006(x2+2)00006(x3+2)00006(x4+2) 41414141 = 4.54.54.54.5
所以最后获得关于的矩阵 X X X的导数为
∂ f ∂ X = [ ∂ f ∂ x 1 ∂ f ∂ x 2 ∂ f ∂ x 3 ∂ f ∂ x 4 ] = [ 4.5 4.5 4.5 4.5 ] \frac{\partial f}{\partial X} = \begin{bmatrix} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2} \\ \frac{\partial f}{\partial x_3} & \frac{\partial f}{\partial x_4} \end{bmatrix} = \begin{bmatrix} 4.5 & 4.5 \\ 4.5 & 4.5 \\ \end{bmatrix} ∂X∂f=[∂x1∂f∂x3∂f∂x2∂f∂x4∂f]=[4.54.54.54.5]
当输出是张量tensor函数时
x = torch.tensor([[1.0, 2, 3],[4, 5, 6],[7, 8, 9]], requires_grad=True)
w = torch.tensor([[1.0, 2, 3],[4, 5, 6]], requires_grad=True)y = torch.matmul(x,w.T)
print(y)
print(torch.ones_like(y))
y.backward(gradient = torch.ones_like(y))
print(x.grad)
输出是
tensor([[ 14., 32.],[ 32., 77.],[ 50., 122.]], grad_fn=<MmBackward0>)
tensor([[1., 1.],[1., 1.],[1., 1.]])
tensor([[5., 7., 9.],[5., 7., 9.],[5., 7., 9.]])
Y = X W T [ y 11 y 21 y 12 y 22 y 13 y 23 ] = [ x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ] [ w 11 w 21 w 12 w 22 w 13 w 23 ] [ y 11 y 21 y 12 y 22 y 13 y 23 ] = [ ( x 11 w 11 + x 12 w 12 + x 13 w 13 ) ( x 11 w 21 + x 12 w 22 + x 13 w 23 ) ( x 21 w 11 + x 22 w 12 + x 23 w 13 ) ( x 21 w 21 + x 22 w 22 + x 23 w 23 ) ( x 31 w 11 + x 32 w 12 + x 33 w 13 ) ( x 31 w 21 + x 32 w 22 + x 33 w 23 ) ] Y = XW^T \\ \begin{bmatrix} y_{11} & y_{21} \\ y_{12} & y_{22} \\ y_{13} & y_{23} \\ \end{bmatrix} = \begin{bmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \\ \end{bmatrix} \begin{bmatrix} w_{11} & w_{21} \\ w_{12} & w_{22} \\ w_{13} & w_{23} \\ \end{bmatrix} \\ \begin{bmatrix} y_{11} & y_{21} \\ y_{12} & y_{22} \\ y_{13} & y_{23} \\ \end{bmatrix} = \begin{bmatrix} (x_{11}w_{11} + x_{12}w_{12} + x_{13}w_{13}) & (x_{11}w_{21} + x_{12}w_{22} + x_{13}w_{23}) \\ (x_{21}w_{11} + x_{22}w_{12} + x_{23}w_{13}) & (x_{21}w_{21} + x_{22}w_{22} + x_{23}w_{23}) \\ (x_{31}w_{11} + x_{32}w_{12} + x_{33}w_{13}) & (x_{31}w_{21} + x_{32}w_{22} + x_{33}w_{23}) \\ \end{bmatrix} Y=XWT y11y12y13y21y22y23 = x11x21x31x12x22x32x13x23x33 w11w12w13w21w22w23 y11y12y13y21y22y23 = (x11w11+x12w12+x13w13)(x21w11+x22w12+x23w13)(x31w11+x32w12+x33w13)(x11w21+x12w22+x13w23)(x21w21+x22w22+x23w23)(x31w21+x32w22+x33w23)
gradient=torch.ones_like(y)用于指定矩阵 Y Y Y中每一项的权重都为1,由矩阵 Y Y Y中元素加权得到的scalar函数为
f ( x , w ) = 1 × y 11 + 1 × y 12 + 1 × y 13 + 1 × y 21 + 1 × y 22 + 1 × y 23 , x = [ x 11 , x 12 , x 13 , x 21 , x 22 , x 23 , x 31 , x 32 , x 33 ] T w = [ w 11 , w 12 , w 13 , w 21 , w 22 , w 23 , w 31 , w 32 , w 33 ] T \begin{aligned} f(\mathrm{x},\mathrm{w}) & = 1\times y_{11}+1\times y_{12}+1\times y_{13}+1\times y_{21}+1\times y_{22}+1\times y_{23}, \\ & \mathrm{x} = [x_{11}, x_{12}, x_{13}, x_{21}, x_{22}, x_{23}, x_{31}, x_{32}, x_{33}]^T \\ & \mathrm{w} = [w_{11}, w_{12}, w_{13}, w_{21}, w_{22}, w_{23}, w_{31}, w_{32}, w_{33}]^T \end{aligned} f(x,w)=1×y11+1×y12+1×y13+1×y21+1×y22+1×y23,x=[x11,x12,x13,x21,x22,x23,x31,x32,x33]Tw=[w11,w12,w13,w21,w22,w23,w31,w32,w33]T
这里不包括复合求导,可以直接计算
∂ f ∂ x = [ ∂ f ∂ x 11 , ∂ f ∂ x 12 , ∂ f ∂ x 13 , ∂ f ∂ x 21 , ∂ f ∂ x 22 , ∂ f ∂ x 23 , ∂ f ∂ x 31 , ∂ f ∂ x 32 , ∂ f ∂ x 33 ] T ∂ f ∂ x = [ w 11 + w 21 , w 12 + w 22 , w 13 + w 23 , w 11 + w 21 , w 12 + w 22 , w 13 + w 23 , w 11 + w 21 , w 12 + w 22 , w 13 + w 23 ] T = [ 5 , 7 , 9 , 5 , 7 , 9 , 5 , 7 , 9 ] T \begin{aligned} \frac{\partial f}{\partial \mathrm{x}} & = \Big[\frac{\partial f}{\partial x_{11}}, \frac{\partial f}{\partial x_{12}}, \frac{\partial f}{\partial x_{13}}, \frac{\partial f}{\partial x_{21}}, \frac{\partial f}{\partial x_{22}}, \frac{\partial f}{\partial x_{23}}, \frac{\partial f}{\partial x_{31}}, \frac{\partial f}{\partial x_{32}}, \frac{\partial f}{\partial x_{33}} \Big]^T \\ \frac{\partial f}{\partial \mathrm{x}} & = \Big[ w_{11} + w_{21}, w_{12} + w_{22}, w_{13} + w_{23}, w_{11} + w_{21}, w_{12} + w_{22}, w_{13} + w_{23}, w_{11} + w_{21}, w_{12} + w_{22}, w_{13} + w_{23} \Big]^T \\ & = [5, 7, 9, 5, 7, 9, 5, 7, 9]^T \end{aligned} ∂x∂f∂x∂f=[∂x11∂f,∂x12∂f,∂x13∂f,∂x21∂f,∂x22∂f,∂x23∂f,∂x31∂f,∂x32∂f,∂x33∂f]T=[w11+w21,w12+w22,w13+w23,w11+w21,w12+w22,w13+w23,w11+w21,w12+w22,w13+w23]T=[5,7,9,5,7,9,5,7,9]T
再写成矩阵的形式则有
∂ f ∂ X = [ 5 7 9 5 7 9 5 7 9 ] \frac{\partial f}{\partial X} = \begin{bmatrix} 5 & 7 & 9 \\ 5 & 7 & 9 \\ 5 & 7 & 9 \\ \end{bmatrix} ∂X∂f= 555777999
再考虑一个更一般求二阶导的情况
x = torch.ones(3, requires_grad=True)
print(x)
y = x * 2
print(y)
z = y * 2
print(z)
v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
z.backward(gradient=v)
print(x.grad)
结果如下
tensor([1., 1., 1.], requires_grad=True)
tensor([2., 2., 2.], grad_fn=<MulBackward0>)
tensor([4., 4., 4.], grad_fn=<MulBackward0>)
tensor([4.0000e-01, 4.0000e+00, 4.0000e-04])
其中
x = [ x 1 , x 2 , x 3 ] T = [ 1 , 1 , 1 ] T y = 2 x = [ y 1 , y 2 , y 3 ] T = [ 2 , 2 , 2 ] T z = 2 y = [ z 1 , z 2 , z 3 ] T = [ 4 , 4 , 4 ] T \begin{aligned} \mathrm{x} & = [x_1,x_2,x_3]^T = [1,1,1]^T \\ \mathrm{y} = 2\mathrm{x} & = [y_1,y_2,y_3]^T = [2,2,2]^T \\ \mathrm{z} = 2\mathrm{y} & = [z_1,z_2,z_3]^T = [4,4,4]^T \end{aligned} xy=2xz=2y=[x1,x2,x3]T=[1,1,1]T=[y1,y2,y3]T=[2,2,2]T=[z1,z2,z3]T=[4,4,4]T
若考虑gradient=torch.tensor([a1,a2,a3], dtype=torch.folat),那么最终加权得到的scalar函数为
f = a 1 z 1 + a 2 z 2 + a 3 z 3 f = a_1 z_1 + a_2 z_2 + a_3 z_3 f=a1z1+a2z2+a3z3
那么对 x \mathrm{x} x求偏导则有
∂ f ∂ x = ∂ y ∂ x ∂ f ∂ y = [ ∂ y 1 ∂ x 1 ∂ y 2 ∂ x 1 ∂ y 3 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 2 ∂ x 2 ∂ y 3 ∂ x 2 ∂ y 1 ∂ x 3 ∂ y 2 ∂ x 3 ∂ y 3 ∂ x 3 ] [ ∂ f ∂ y 1 ∂ f ∂ y 2 ∂ f ∂ y 3 ] = [ 2 2 2 ] [ 2 a 1 2 a 2 2 a 3 ] = [ 4 a 1 , 4 a 2 , 4 a 3 ] T \begin{aligned} \frac{\partial f}{\partial \mathrm{x}} & = \frac{\partial \mathrm{y}}{\partial \mathrm{x}} \frac{\partial f}{\partial \mathrm{y}} \\ & = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_2}{\partial x_1} & \frac{\partial y_3}{\partial x_1} \\ \frac{\partial y_1}{\partial x_2} & \frac{\partial y_2}{\partial x_2} & \frac{\partial y_3}{\partial x_2} \\ \frac{\partial y_1}{\partial x_3} & \frac{\partial y_2}{\partial x_3} & \frac{\partial y_3}{\partial x_3} \\ \end{bmatrix} \begin{bmatrix} \frac{\partial f}{\partial y_1} \\ \frac{\partial f}{\partial y_2} \\ \frac{\partial f}{\partial y_3} \\ \end{bmatrix} \\ & = \begin{bmatrix} 2 & & \\ & 2 & \\ & & 2 \end{bmatrix} \begin{bmatrix} 2 a_1 \\ 2 a_2 \\ 2 a_3 \\ \end{bmatrix} \\ & = [4a_1, 4a_2, 4a_3]^T \end{aligned} ∂x∂f=∂x∂y∂y∂f= ∂x1∂y1∂x2∂y1∂x3∂y1∂x1∂y2∂x2∂y2∂x3∂y2∂x1∂y3∂x2∂y3∂x3∂y3 ∂y1∂f∂y2∂f∂y3∂f = 222 2a12a22a3 =[4a1,4a2,4a3]T
一些启示

Reference
参考教程1
参考教程2
相关文章:

Pytorch Tutorial【Chapter 2. Autograd】
Pytorch Tutorial 文章目录 Pytorch TutorialChapter 2. Autograd1. Review Matrix Calculus1.1 Definition向量对向量求导1.2 Definition标量对向量求导1.3 Definition标量对矩阵求导 2.关于autograd的说明3. grad的计算3.1 Manual手动计算3.2 backward()自动计算 Reference C…...

Python第三方库国内镜像下载地址
Python第三方库国内镜像下载地址 一、清华大学二、中国科技大学三、安装方法 一、清华大学 https://pypi.tuna.tsinghua.edu.cn/simple 二、中国科技大学 https://pypi.mirrors.ustc.edu.cn/simple 三、安装方法 例如 pyhook3 插件的安装方法,执行下面命令安装…...
服务端机器一般部署在哪里)
从浏览器输入url到页面加载(七)服务端机器一般部署在哪里
前言 上一节,我们说到了CDN和路由器的关系,说到了公有地址,说到了通信线路服务,这一节跳过那些看不懂的深层知识,直接开始说web服务器。 1. 服务端机器为什么不部署在公司内部 记得在之前的一段时间里,公…...
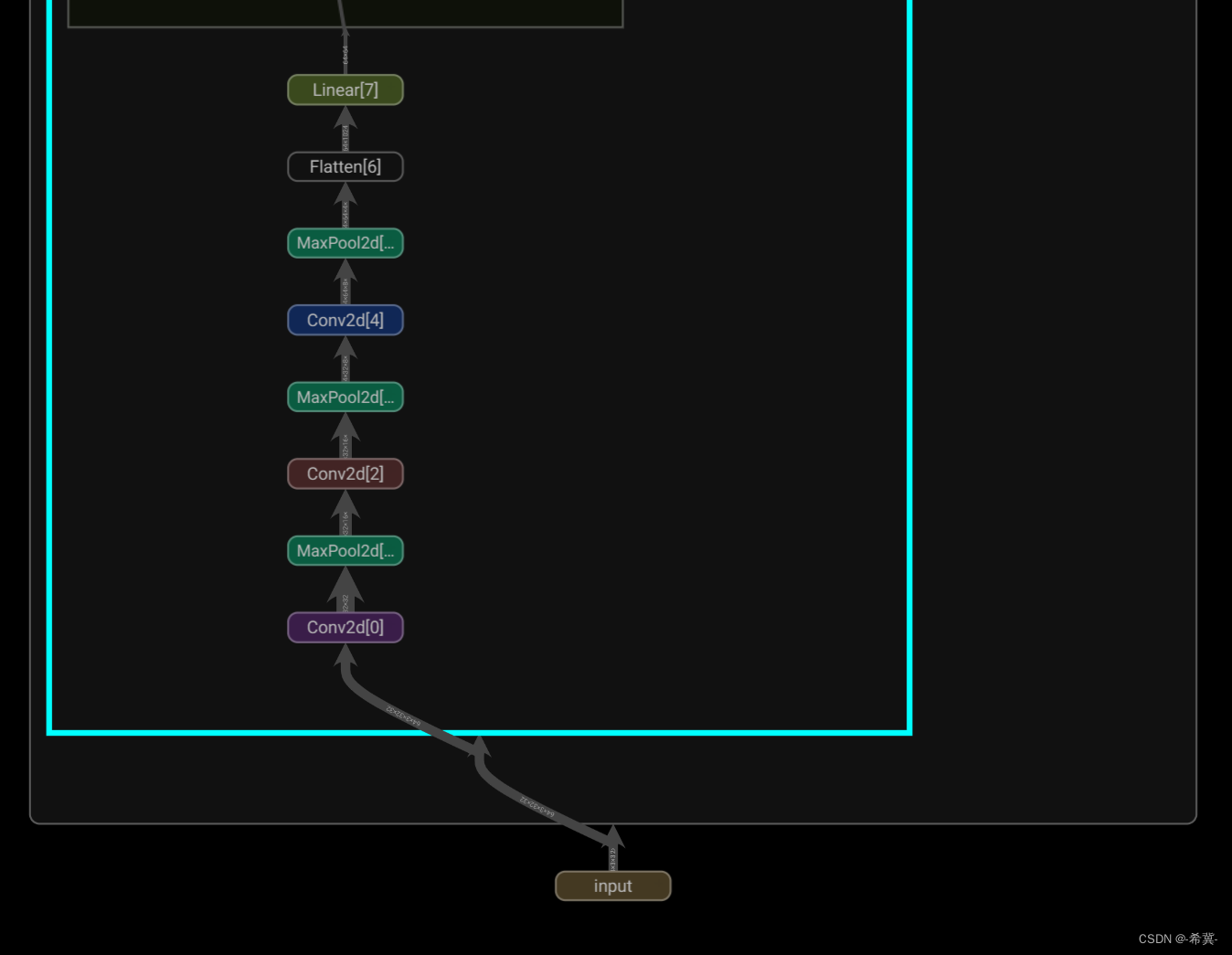
Pytorch深度学习-----神经网络之Sequential的详细使用及实战详解
系列文章目录 PyTorch深度学习——Anaconda和PyTorch安装 Pytorch深度学习-----数据模块Dataset类 Pytorch深度学习------TensorBoard的使用 Pytorch深度学习------Torchvision中Transforms的使用(ToTensor,Normalize,Resize ,Co…...
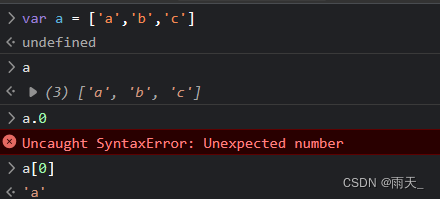
安全基础 --- https详解 + 数组(js)
CIA三属性:完整性(Confidentiality)、保密性(Integrity)、可用性(Availability),也称信息安全三要素。 https 核心技术:用非对称加密传输对称加密的密钥,然后…...

vue加载大量数据优化
在Vue中加载大量数据并形成列表时,可以通过以下方法来优化性能: 分页加载:不要一次性加载所有的数据,而是分批加载数据,每次只加载当前页需要显示的数据量。可以使用第三方库如vue-infinite-loading来实现无限滚动加载…...

WebRTC 之音视频同步
在网络视频会议中, 我们常会遇到音视频不同步的问题, 我们有一个专有名词 lip-sync 唇同步来描述这类问题,当我们看到人的嘴唇动作与听到的声音对不上的时候,不同步的问题就出现了 而在线会议中, 听见清晰的声音是优先…...
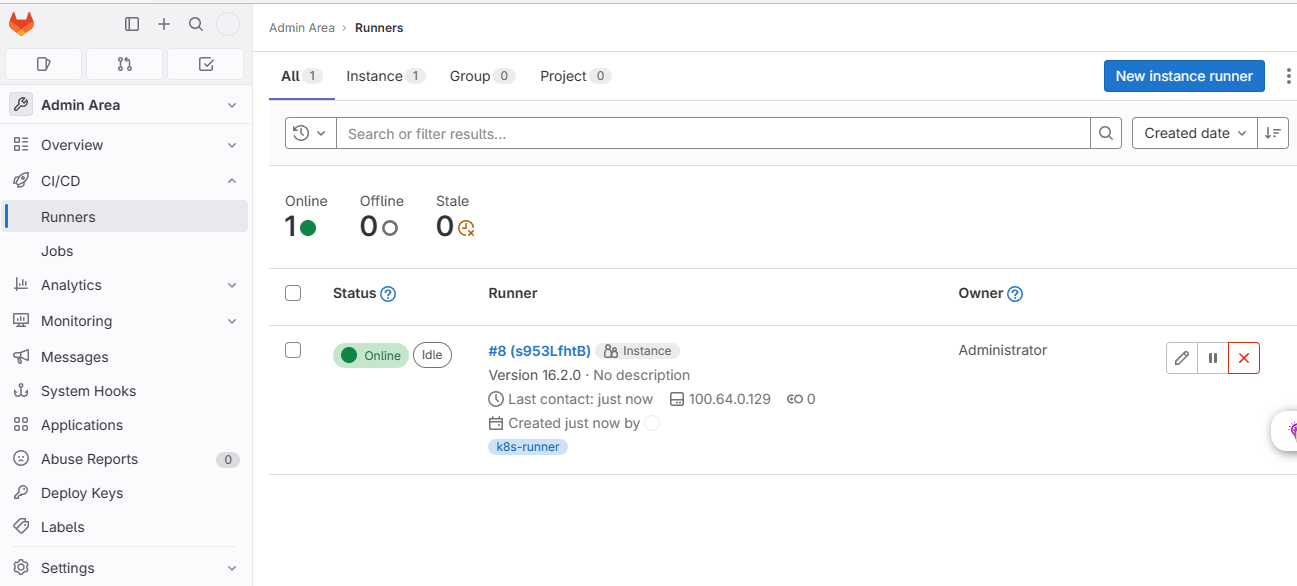
kubernetes基于helm部署gitlab-runner
kubernetes基于helm部署gitlab-runner 这篇博文介绍如何在 Kubernetes 中使用helm部署 GitLab-runner。 先决条件: 已运行的 Kubernetes 集群已运行的 gitlab 实例 项目地址:https://gitlab.com/gitlab-org/charts/gitlab-runner 官方文档ÿ…...

深度学习和OpenCV的对象检测(MobileNet SSD图像识别)
基于深度学习的对象检测时,我们主要分享以下三种主要的对象检测方法: Faster R-CNN(后期会来学习分享)你只看一次(YOLO,最新版本YOLO3,后期我们会分享)单发探测器(SSD,本节介绍,若你的电脑配置比较低,此方法比较适合R-CNN是使用深度学习进行物体检测的训练模型; 然而,…...
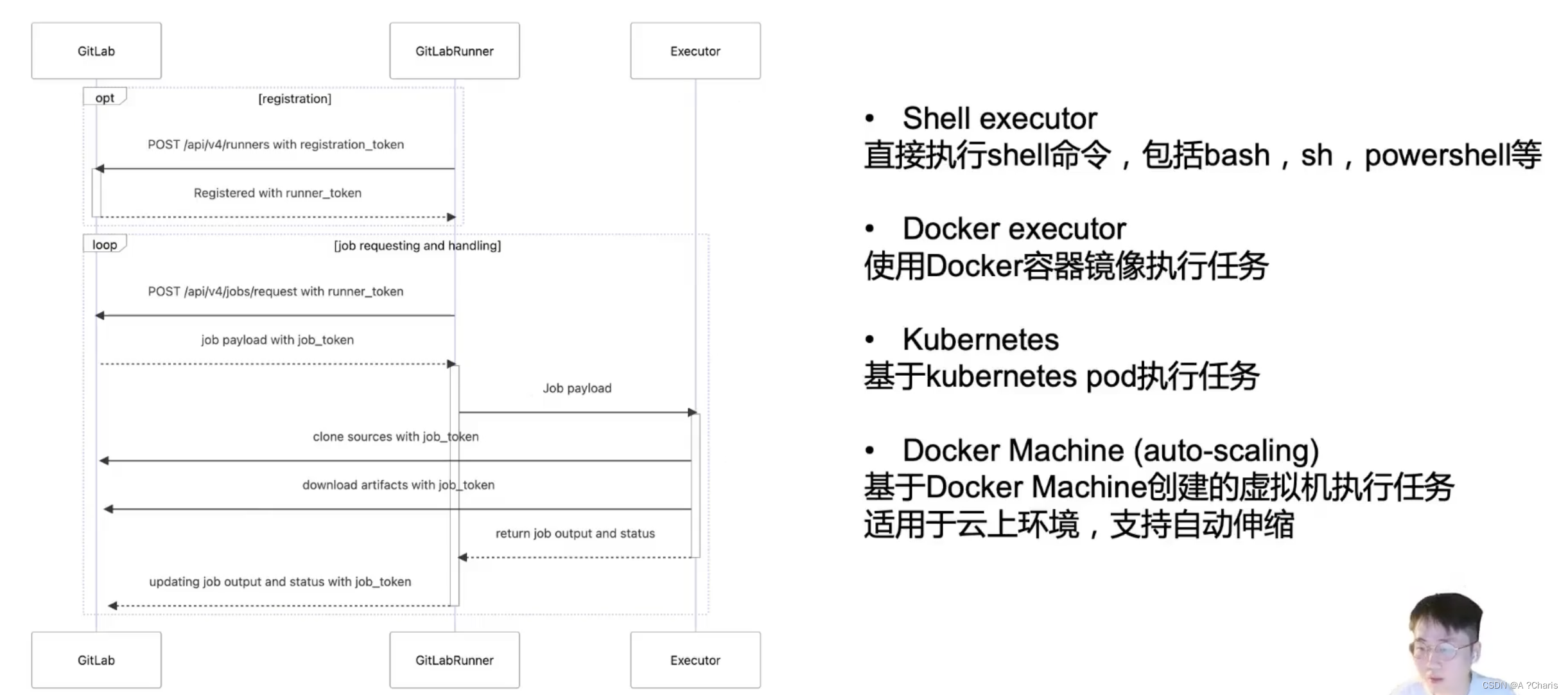
Gitlab CI/CD笔记-第一天-GitOps和以前的和jenkins的集成的区别
一、GitOps-CI/CD的流程图与Jenkins的流程图 从上图可以看到: GitOps与基于Jennkins技术栈的CI/CD流程,无法从Jenkins集成其他第三方开源的项目来实现换成了Gitlab来进行集成。 好处在于:CI 一个工具Gitlab就行了,但CD部分依旧是…...

有关OpenBSD, NetBSD, FreeBSD -- 与GPT对话
1 介绍一下 - OpenBSD, NetBSD, FreeBSD 当谈论操作系统时,OpenBSD、NetBSD和FreeBSD都是基于BSD(Berkeley Software Distribution)的操作系统,它们各自是独立开发的,并在BSD许可下发布。这些操作系统有很多共同点,但也有一些差异。以下是对它们的简要介绍: OpenBSD: O…...
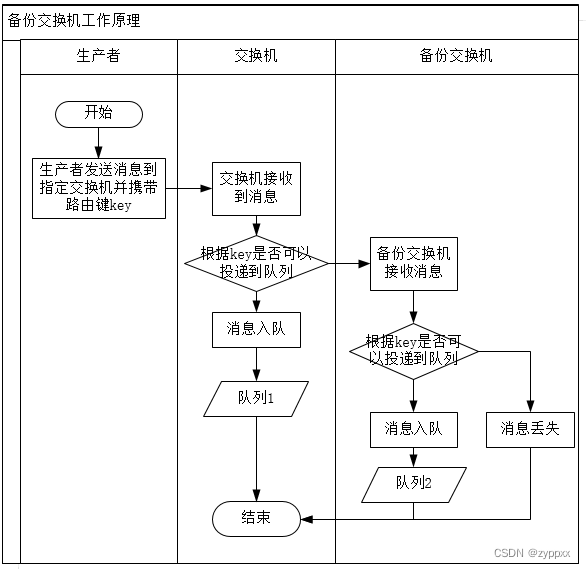
RabbitMQ 备份交换机和死信交换机
为处理生产者生产者将消息推送到交换机中,交换机按照消息中的路由键即自身策略无法将消息投递到指定队列中造成消息丢失的问题,可以使用备份交换机。 为处理在消息队列中到达TTL的过期消息,可采用死信交换机进行消息转存。 通过上述描述可知&…...

Linux 中利用设备树学习Ⅳ
系列文章目录 第一章 Linux 中内核与驱动程序 第二章 Linux 设备驱动编写 (misc) 第三章 Linux 设备驱动编写及设备节点自动生成 (cdev) 第四章 Linux 平台总线platform与设备树 第五章 Linux 设备树中pinctrl与gpio(…...
使用Spring Initializr方式构建Spring Boot项目
除了可以使用Maven方式构建Spring Boot项目外,还可以通过Spring Initializr方式快速构建Spring Boot项目。从本质上说,Spring lnitializr是一个Web应用,它提供了一个基本的项目结构,能够帮助我们快速构建一个基础的Spring Boot项目…...
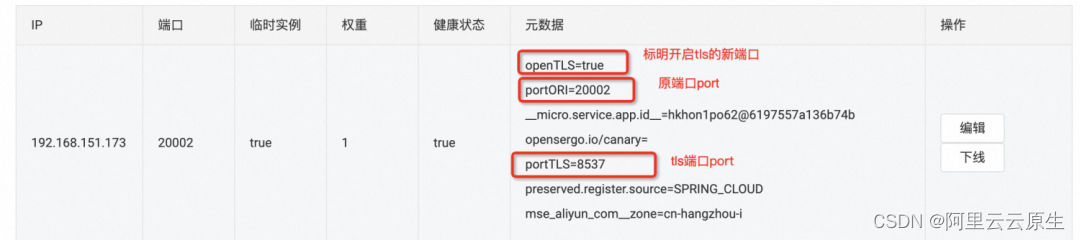
Sentinel 2.0 微服务零信任的探索与实践
作者:涯客、十眠 从古典朴素的安全哲学谈起 网络安全现状 现在最常见的企业网络安全架构便是在企业网络边界处做安全防护,而在企业网络内部不做安全防范。这确实为企业的安全建设省了成本也为企业提供了一定的防护能力。但是这类比于现实情况的一个小…...
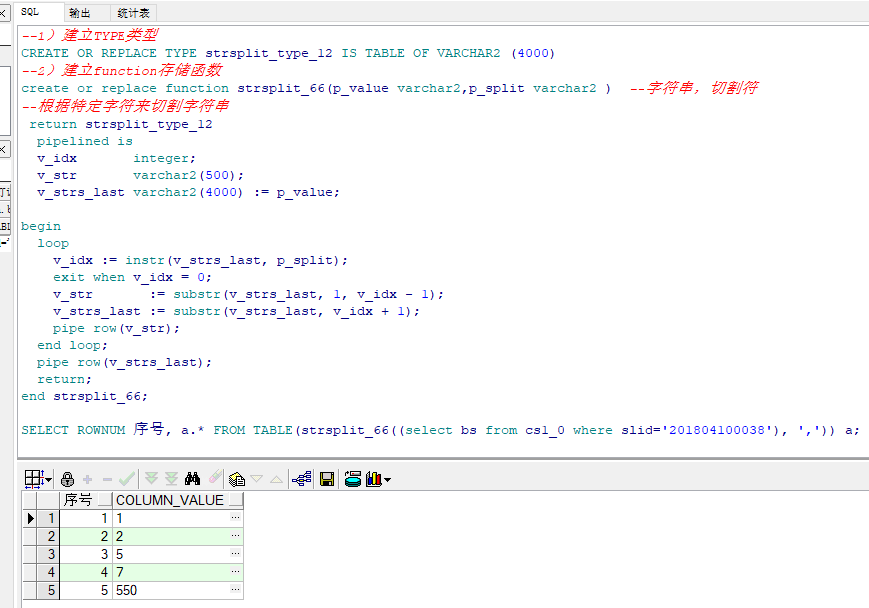
Oracle以逗号分隔的字符串拆分为多行数据实例详解
前言 近期在工作中遇到某表某字段是可扩展数据内容,信息以逗号分隔生成的,现需求要根据此字段数据在其它表查询相关的内容展现出来,第一想法是切割数据,以逗号作为切割符,以下为总结的实现方法,以供大家参…...
harbor仓库安装部署(1.6.1)
目录 1、关闭防火墙 2、安装docker-ce(所有主机) 3、配置阿里云镜像加速器 4、部署Docker Compose 服务 5、部署 Harbor 服务 6、下载 Harbor 安装程序(两台harbor主机) 7、配置 Harbor 参数文件 8、启动并安装 Harbor …...

FastAPI 构建 API 高性能的 web 框架(一)
如果要部署一些大模型一般langchainfastapi,或者fastchat, 先大概了解一下fastapi,本篇主要就是贴几个实际例子。 官方文档地址: https://fastapi.tiangolo.com/zh/ 1 案例1:复旦MOSS大模型fastapi接口服务 来源:大语言模型工程…...

Spring框架中的Bean的生命周期
Spring Bean 的生命周期总体分为四个阶段:实例化 》属性注入》初始化》销毁 实例化: (1)实例化bean:根据配置文件中Bean的定义,利用java Reflection 反射技术创建Bean的实例! 属性注入&#…...
vue3-ts-vite:vue 项目 配置 多页面应用
一、Vue项目,什么是多页面应用 Vue是一种单页面应用程序(SPA)框架,这意味着Vue应用程序通常只有一个HTML页面,而在该页面上进行动态的内容更改,而不是每次都加载新的HTML页面。 但是,有时候我…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
