最后一次模拟考试题解
哦我想这不用看都知道是为了水任务
T1 黑白染色
其实这题有原

什么手写体 md (指 markdown)
分析
首先这题如果你题目没看错的话 ,会发现其实他是 n × m n \times m n×m 让你求 n × n n \times n n×n 的区域内的点(不会只有我一个人题目看错了罢
然后我们会发现其实我们只关心每一列放了多少,并不关心是怎么放的(这一步可以用组合数算出来)
波利亚说过解题时可以回到定义上去 , 所以列出公式(这里 n u m [ i ] num[i] num[i] 代表每一列放置点的数量)
∑ i = 1 n n u m [ i ] = k ∑ i = 2 n + 1 n u m [ i ] = k \begin{matrix} \sum_{i=1}^n num[i] = k \\ \sum_{i=2}^{n+1} num[i] = k\end{matrix} ∑i=1nnum[i]=k∑i=2n+1num[i]=k
两式相减就可以得到: n u m [ i ] = n u m [ i + n ] num[i] = num[i+n] num[i]=num[i+n]
所以我们就发现了所有模 n n n 余数相同的列的值时一样的
剩下的我就不知道了
Code
我讲不来但是我有代码
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define int long long
const int N = 1e6+10;
const int M = 1e5+10;
const int mod = 1e9+7;
using namespace std;
int c[200][200];
int d[200][200];
int dp[200][10005];
int n,m,k;
int ksm(int a, int b){int x = a,ans = 1;while(b){if(b & 1){ans = ans * x % mod;}x = x * x % mod;b >>= 1;}return ans;
}
signed main(){freopen("discolour.in","r",stdin);freopen("discolour.out","w",stdout);cin >> n >> m >> k;for(int i =1;i <= 100; i++){c[i][0] = c[i][i] = 1;for(int j = 1; j < i; j++){c[i][j] = (c[i-1][j] + c[i-1][j-1]) % mod;}}for(int i = 1;i <= n; i++){for(int j = 0; j <= n; j++){d[i][j] = ksm(c[n][j],m/n+(m/n*n+i<=m));
// cout << d[i][j] << endl;}}dp[0][0] = 1;for(int i = 1; i <= n; i++){for(int j = 0; j <= min(k,n*i); j++){for(int kk = 0; kk <= min(j,n); kk++){dp[i][j] = (dp[i][j] + dp[i-1][j-kk]*d[i][kk] % mod)%mod;
// cout << dp[i][j] << endl;}}}cout << dp[n][k];return 0;
}当时还把 colour 打成了 color , 幸好最后改回来了
cspj的时候文件保存按成了撤销痛失100分我不说是谁
T2 造城墙

有一说一这题数据是真的弱啊
首先,对于 40 % 40\% 40% 的数据,可以直接状压
然后对于另外 20 % 20\% 20% 的数据可以直接染色跑二分图
分析
正文开始
看到这题其实像 czy 那样的猥琐小子大佬,第一反应应该就是网络流罢,对棋盘黑白染色,这个应该不难想
没错这个跟这道题的正解没关系
但是可以帮助你理解思路
注意下面均用 0 代表偶数 1 代表奇数
首先一个很显然的贪心就是 所有横着的砖块肯定放在最顶上
如果你用脚造了几组数据玩玩的话你会发现,所有横着放的砖块会构成多个倒三角
like this
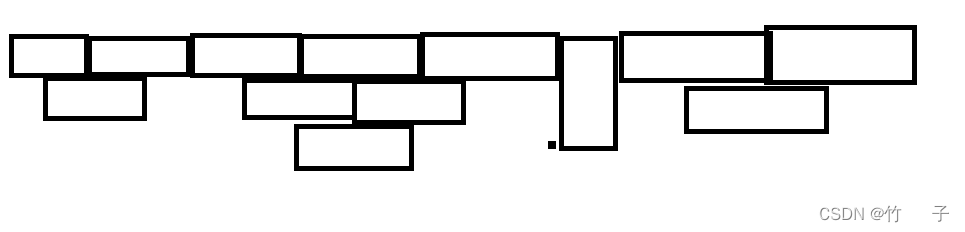
如果对于这个倒三角还有点懵的可以在这里停一下搞清楚先
所以我们考虑维护当前列倒三角的高度
让我们随便造几组数据(下面的数据均是空白格的个数)
一列一列枚举:1 高度为 1, 10 高度为 2 , 101 高度为 3,1011 高度为3 , 10110 高度为2
这里发现什么,当出现 00 或者 11 的时候高度不会再增加,并且下一行如果奇偶性不同高度还会减 1 (其实这个应该看图就知道了罢
如果您无法理解
可以把他看成一个黑白染色,每一列不能匹配的黑格子都会被放到最顶上,这样一列一列的黑格子剩下来就是高度了
那接下来就考虑维护高度,有了上面的规律之后,我们记 b l a c k black black 为当前的高度(黑格子数)
不难发现,如果当前的空白格数小于黑格子数,肯定就不能满足。如果空白格数减黑格子数为奇数,那黑格子数就要加一,如果为偶数,那就减一
最后别忘了在黑格子减一的时候和 0 取 m a x max max (其实不取你也能得到 80 分的好成绩)
Code
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define int long long
const int N = 1e6+10;
const int M = 1e5+10;using namespace std;
int n;
priority_queue<pair<int,int>,vector<pair<int,int> > , greater<pair<int,int> > > q;
int x,y,z;signed main(){freopen("chicken.in","r",stdin);freopen("chicken.out","w",stdout);cin >> n;cin >> x >> y >> z;int t,a;cin >> t >> a;q.push(make_pair(t-z+y,a));int sum = a;for(int i = 2; i <= n; i++){cin >> t >> a;while(a){int xx = q.top().first,num = q.top().second;if(xx + x <= t){
// cout << xx << " " << num << endl;q.pop();if(num > a){num -= a;q.push(make_pair(xx,num));q.push(make_pair(max(xx+x+z,t-y+z),a));a = 0;}else{a -= num;q.push(make_pair(max(xx+x+z,t-y+z),num));}
// cout << xx << " xx ";
// cout << max(xx+x+y,t-z+y) << " xx ";}else{q.push(make_pair(t-y+z,a));
// cout << t-y+z << " " << a << endl;sum += a;a = 0;
// cout << t-z+y << " yy ";}}
// cout << endl;}cout << sum;return 0;
}T3 炸鸡

这手写的 LaTeX \LaTeX LATEX 是真的一言难尽
分析
这题有一个很重要的性质就是 :同一份订单中,不会有任何一口锅做超过一份的鸡(因为鸡的保存时间小于制作时间)
接下来考虑贪心
虽然我们是非常单纯美好的,但是这题的做法非常的黑心,那就是 给顾客的鸡能多接近保质期就多接近保质期
然后我们就可以用优先队列维护每口锅最早开始的闲置时间,然后每次取最早的就行,如果没有锅满足要求那就新买几口锅 为了让顾客吃上临近保质期的鸡我还新买锅我真是太伟大了)
写代码的时候记得搞清楚每口锅最早开始闲置的时间是什么
好的我们写完了这个非常czy的代码,定睛一看,忽然发现,数据范围是 1 0 9 10^9 109 而不是 10
那这样我们一个一个丢肯定不对,那么怎么办呢?
如果你把每次取出的锅的时间都输出来,你会发现,有很多锅的时间其实是一样的
(别问我为什么要输出,因为当时把 y , z y,z y,z 看反了)
这样想到什么? 没错往堆里面丢 p a i r pair pair 不就好了吗
Code
这里有个小技巧就是一开始就把第一次所用的锅都扔进去,这样可以防止越界和代码打漏
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define int long long
const int N = 1e6+10;
const int M = 1e5+10;using namespace std;
int n;
priority_queue<pair<int,int>,vector<pair<int,int> > , greater<pair<int,int> > > q;
int x,y,z;signed main(){freopen("chicken.in","r",stdin);freopen("chicken.out","w",stdout);cin >> n;cin >> x >> y >> z;int t,a;cin >> t >> a;q.push(make_pair(t-z+y,a));int sum = a;for(int i = 2; i <= n; i++){cin >> t >> a;while(a){int xx = q.top().first,num = q.top().second;if(xx + x <= t){
// cout << xx << " " << num << endl;q.pop();if(num > a){num -= a;q.push(make_pair(xx,num));q.push(make_pair(max(xx+x+z,t-y+z),a));a = 0;}else{a -= num;q.push(make_pair(max(xx+x+z,t-y+z),num));}
// cout << xx << " xx ";
// cout << max(xx+x+y,t-z+y) << " xx ";}else{q.push(make_pair(t-y+z,a));
// cout << t-y+z << " " << a << endl;sum += a;a = 0;
// cout << t-z+y << " yy ";}}
// cout << endl;}cout << sum;return 0;
}T4 骑士与国王

这题其实就是个容斥对吧(逃)
Code
我这题没打,那就放一下 x h g u a ⋅ h y x xhgua\cdot hyx xhgua⋅hyx 大帝的代码罢
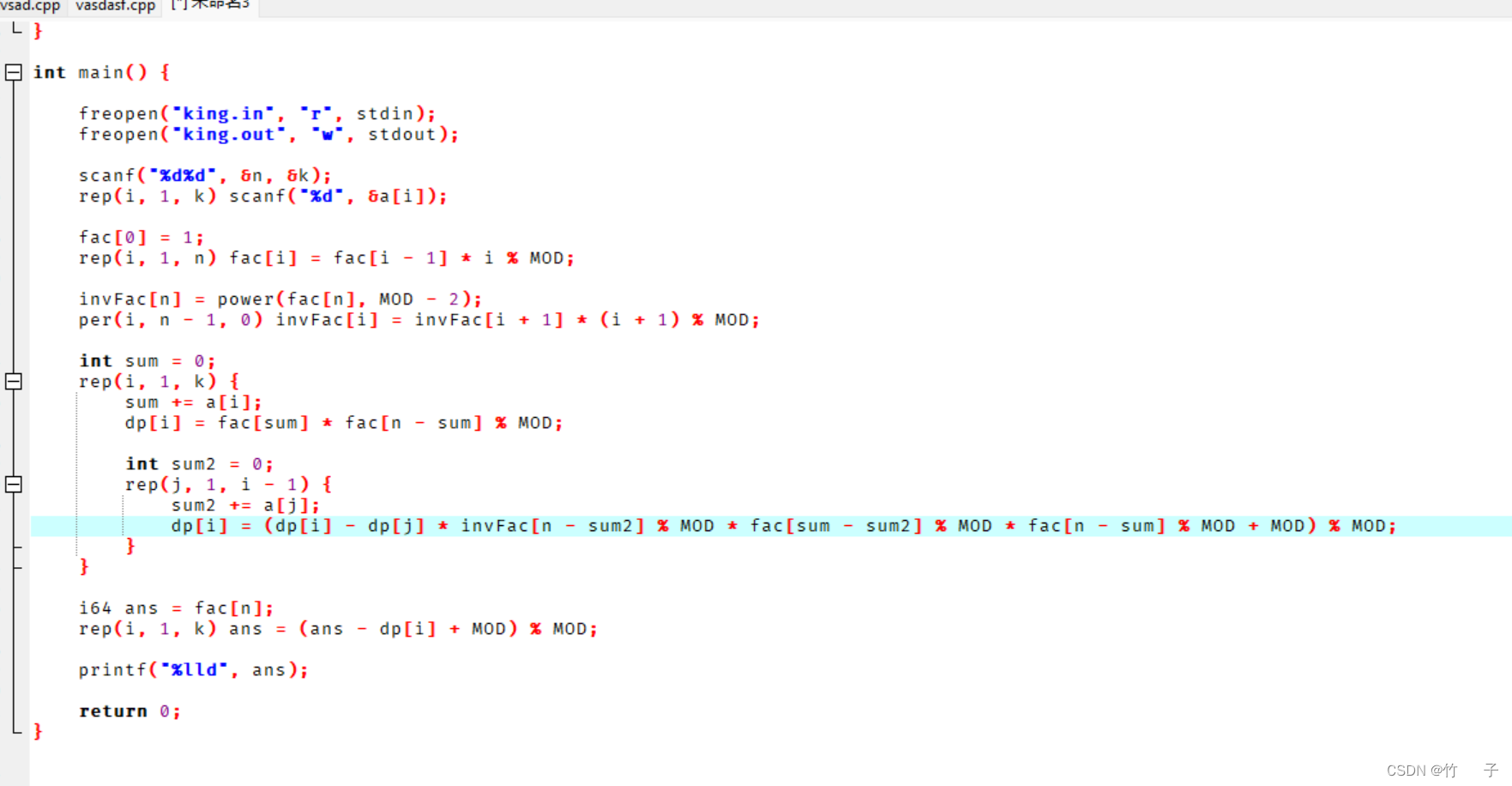
黄瓜好吃,拜谢黄瓜!!!
结语
谁家 noip 3道数学题起步啊
谁家 noip 3小时不到啊
谁家 noip 有人踹电源线啊
有一说一 OI这玩意真的运气成分很高
我爱优先队列 ! 优先队列好闪 拜谢优先队列!!! 以后找对象就找优先队列这样的 ! ! ! \begin{matrix}\color{white}{我爱优先队列!} \\ \color{white}{优先队列好闪\ 拜谢优先队列!!!}\\ \color{white}{以后找对象就找优先队列这样的!!!}\end{matrix} 我爱优先队列!优先队列好闪 拜谢优先队列!!!以后找对象就找优先队列这样的!!!
相关文章:

最后一次模拟考试题解
哦我想这不用看都知道是为了水任务 T1 黑白染色 其实这题有原 什么手写体 md (指 markdown) 分析 首先这题如果你题目没看错的话 ,会发现其实他是 n m n \times m nm 让你求 n n n \times n nn 的区域内的点(不会只有我一个人题目看错了罢 然后我们会发现…...
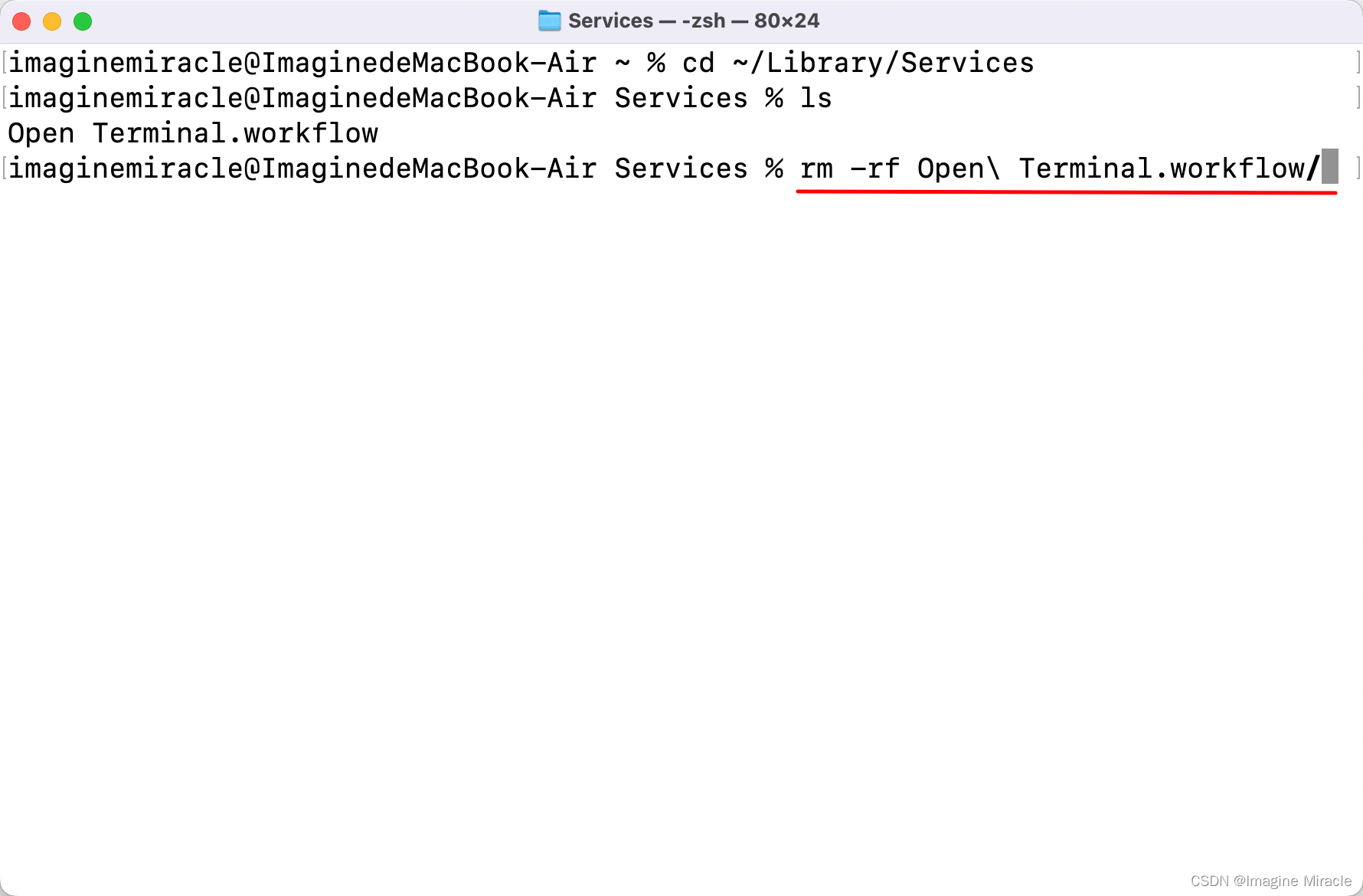
Mac 创建和删除 Automator 工作流程,设置 Terminal 快捷键
1. 创建 Automator 流程 本文以创建一个快捷键启动 Terminal 的自动操作为示例。 点击打开 自动操作; 点击 新建文稿 点击 快速操作 选择 运行 AppleScript 填入以下内容 保存名为 “Open Terminal” 打开 设置 > 键盘,选择 键盘快捷键 以此选择 服…...

2023华为OD机试真题B卷 Java 实现【最长的元音串】
前言 本题使用Java解答,如果需要Python代码,链接 题目 给定一个只由英文字母(a-z, A-Z)组成的字符串,找出其中最长的只包含元音字母(a, e, i, o, u, A, E, I, O, U)的子串,并返回其长度。如果不存在元音子串,则返回0。 输入: 一个由英文字母组成的字符串,长度大…...

网络防御之传输安全
1.什么是数据认证,有什么作用,有哪些实现的技术手段? 数据认证是一种权威的电子文档 作用:它能保证数据的完整性、可靠性、真实性 技术手段有数字签名、加密算法、哈希函数等 2.什么是身份认证,有什么作用,有哪些…...
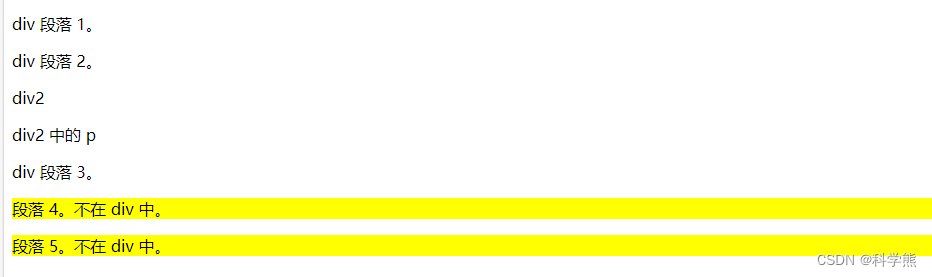
【css】组合器
组合器是解释选择器之间关系的某种机制。在简单选择器器之间,可以包含一个组合器,从而实现简单选择器难以达到的效果。 CSS 中有四种组合器: 后代选择器 (空格):匹配属于指定元素后代的所有元素,示例:div …...

HTTPS、TLS加密传输
HTTPS、TLS加密传输 HTTPS、TLS加密传输1、HTTPS(HyperText Transfer Protocol Secure)2、TLS HTTPS、TLS加密传输 1、HTTPS(HyperText Transfer Protocol Secure) HTTPS(HyperText Transfer Protocol Secure&#x…...

docker frp 搭建 http + stcp 代理
所需服务器 2台 一台具有国外公网ip 一台具有国内 ip 内网外网都可以 外公网ip服务器配置如下 cat docker-compose.yamlversion: "2" services:frps:image: alpine:latesthostname: frpsrestart: alwayscontainer_name: frpsprivileged: trueuser: rootcommand: […...
项目出bug,找不到bug,如何拉回之前的版本
1.用gitee如何拉取代码 本文为转载于「闪耀太阳a」的原创文章原文链接:https://blog.csdn.net/Gufang617/article/details/119929145 怎么从gitee上拉取代码 1.首先找到gitee上想要拉取得代码URL地址 点击复制这里的https地址 1 ps:(另外一种方法&…...
vue-cli
vue-cli脚手架 案例一: 案例二: 案例三: 一、脚手架简介 Vue脚手架是Vue官方提供的标准化开发工具(开发平台),它提供命令行和UI界面,方便创建vue工程、配置第三方依赖、编译vue工程 1. …...
的不正确)
android获取屏幕分辨率的正确方法;获取到分辨率(垂直方向像素)的不正确
我通过下面的方法去获取屏幕分辨率的,但获取到的分辨率有时会不准确。原因是此方法有时候会忽略一些布局或控件的高度,从而得不到正确的高度。 public static String getDeviceResolution(Context context){//从系统服务中获取窗口管理器WindowManager w…...

机器学习笔记之优化算法(八)简单认识Wolfe Condition的收敛性证明
机器学习笔记之优化算法——简单认识Wolfe Condition收敛性证明 引言回顾: Wolfe \text{Wolfe} Wolfe准则准备工作推导条件介绍推导结论介绍 关于 Wolfe \text{Wolfe} Wolfe准则收敛性证明的推导过程 引言 上一节介绍了非精确搜索方法—— Wolfe \text{Wolfe} Wolf…...

通过win+r安装jupyter报错
通过pip install jupyter安装jupyter报错处理办法 1、python 更新到最新版,最好多执行几次后在安装jupyter python.exe -m pip install --upgrade pip 2、通过镜像安装 pip install jupyter --force-reinstall pip -i http://pypi.douban.com/simple/ --trusted-h…...

C#声明一个带返回值的委托
1、声明 public delegate string TestDel(string str); 2、使用 TestDel t; t (string str) > str; t (string str) > str "1"; t (string str) > str "2"; t (string str) > str "3"; Console.WriteLine(t ("hhhh&qu…...

Flutter 自定义view
带进度动画的圆环。没gif,效果大家自行脑补。 继承CustomPainter,paint()方法中拿到canvas,绘制API和android差不多。 import package:flutter/material.dart;class ProgressRingPainter extends CustomPainter {double strokeWidth 20;Col…...

Ubuntu新装系统报错:sudo: vim:找不到命令
问题: 新安装的老版本Ubuntu系统,发现在使用vim命令的时候报错: sudo:vim:找不到命令 解决办法 这是因为没有安装vim,直接运行下面命令安装vim sudo apt-get install vim...

Vue3自定义简单的Swiper滑动组件-触控板滑动鼠标滑动左右箭头滑动-demo
代码实现了一个基本的滑动功能,通过鼠标按下、鼠标松开和鼠标移动事件来监听滑动操作。 具体实现逻辑如下: 在 onMounted 钩子函数中,我们为滚动容器添加了三个事件监听器:mousedown 事件:当鼠标按下时,设置…...
三个主流数据库(Oracle、MySQL和SQL Server)的“单表造数
oracle 1.创建表 CREATE TABLE "YZH2_ORACLE" ("VARCHAR2_COLUMN" VARCHAR2(20) NOT NULL ENABLE,"NUMBER_COLUMN" NUMBER,"DATE_COLUMN" DATE,"CLOB_COLUMN" CLOB,"BLOB_COLUMN" BLOB,"BINARY_DOUBLE_COLU…...

TypeScript 中【class类】与 【 接口 Interfaces】的联合搭配使用解读
导读: 前面章节,我们讲到过 接口(Interface)可以用于对「对象的形状(Shape)」进行描述。 本章节主要介绍接口的另一个用途,对类的一部分行为进行抽象。 类配合实现接口 实现(impleme…...
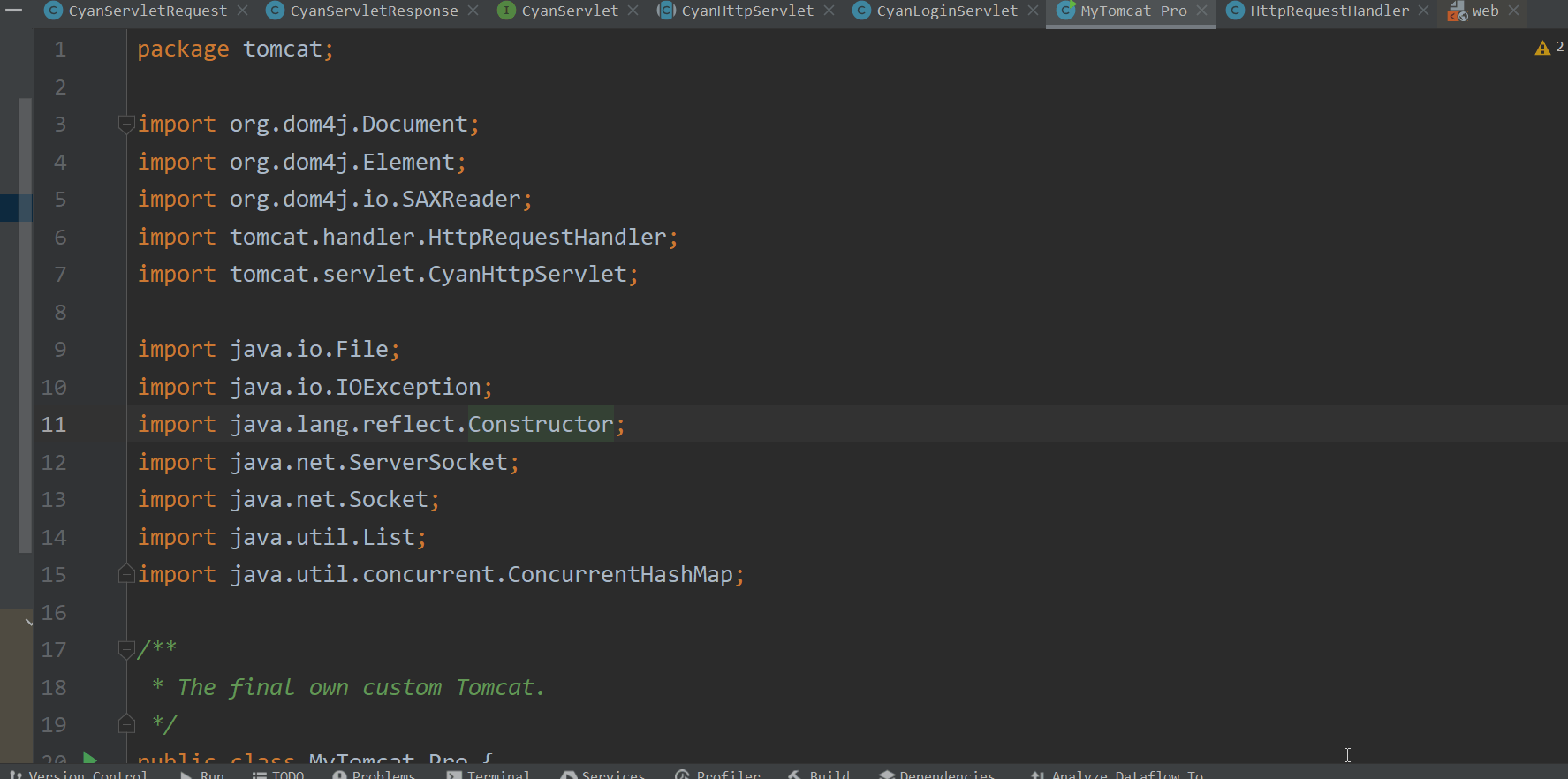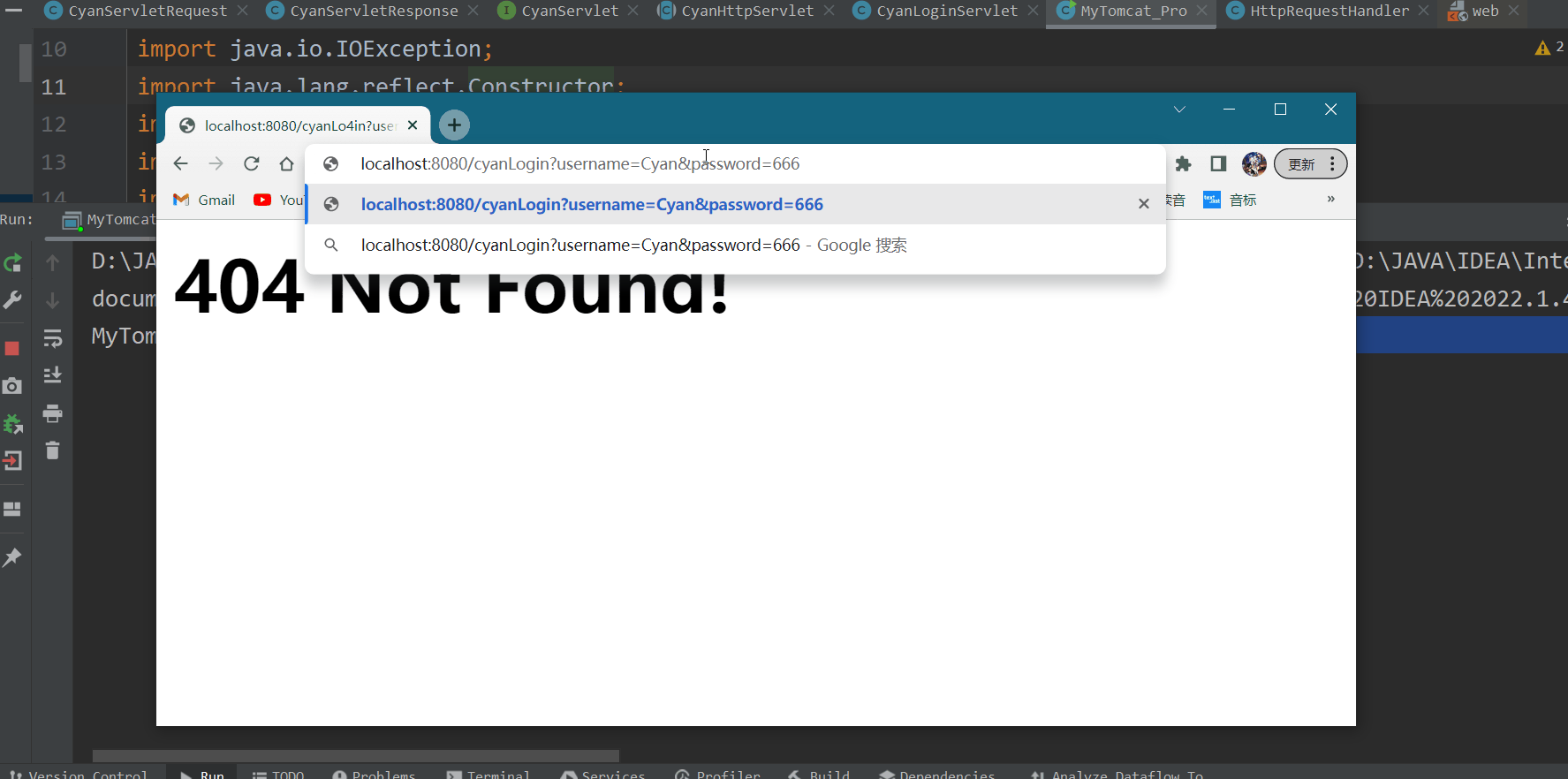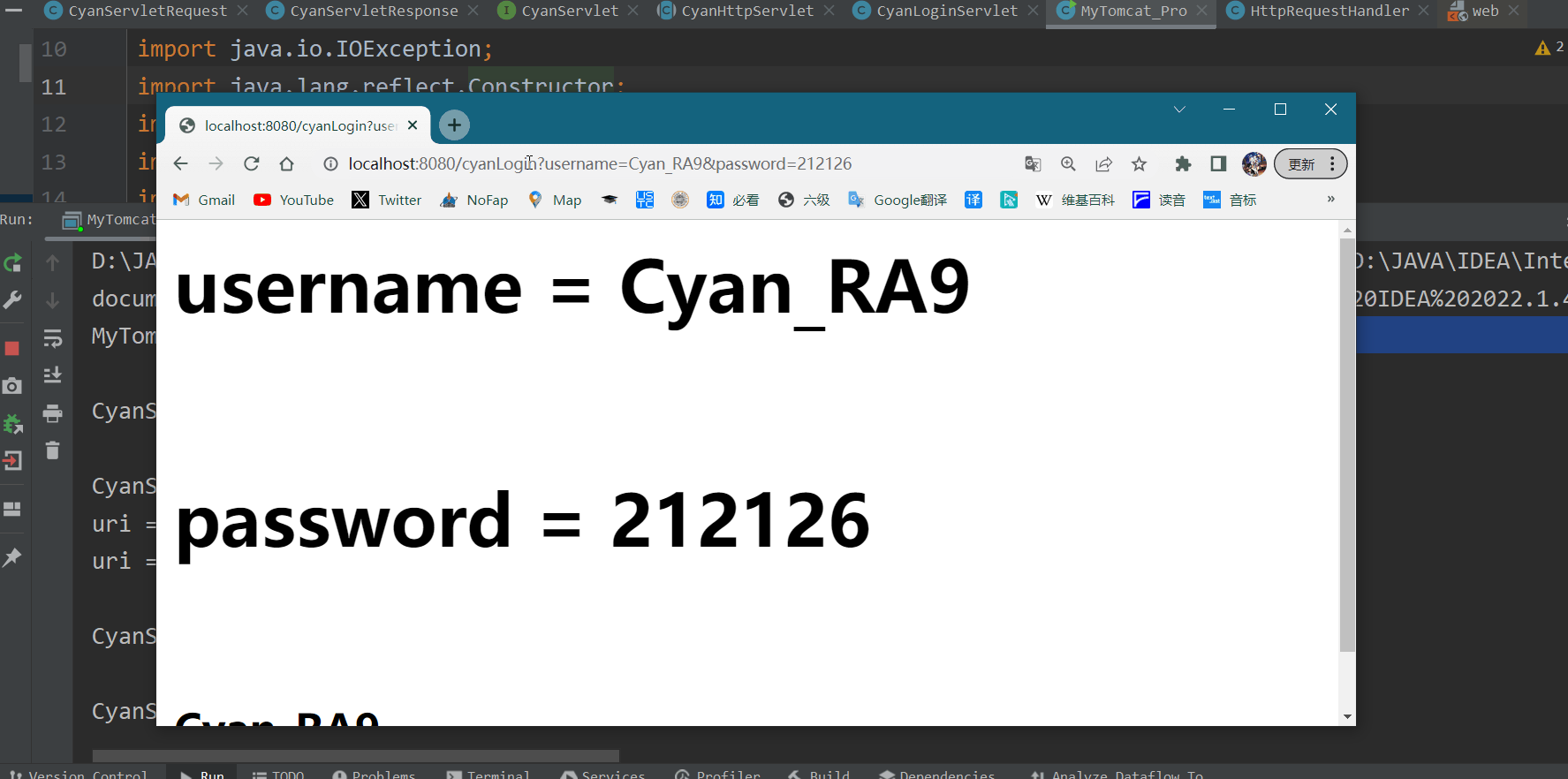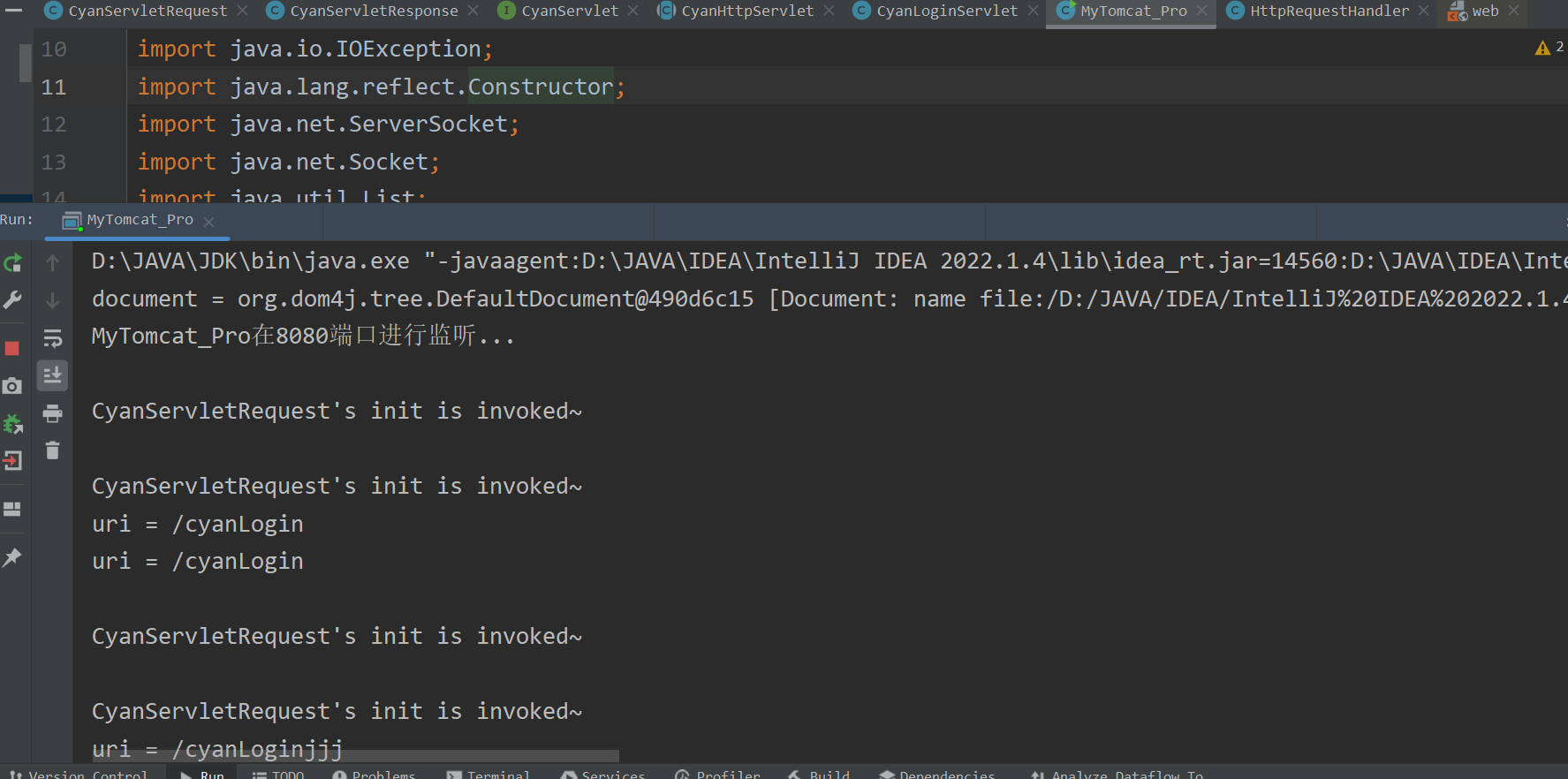
JavaWeb 手写Tomcat底层机制
目录 一、Tomcat底层整体架构 1.简介 : 2.分析图 : 3.基于Socket开发服务端的流程 : 4.打通服务器端和客户端的数据通道 : 二、多线程模型的实现 1.思路分析 : 2.处理HTTP请求 : 3.自定义Tomcat : 三、自定义Servlet规范 1. HTTP请求和响应 : 1 CyanServletRequest …...
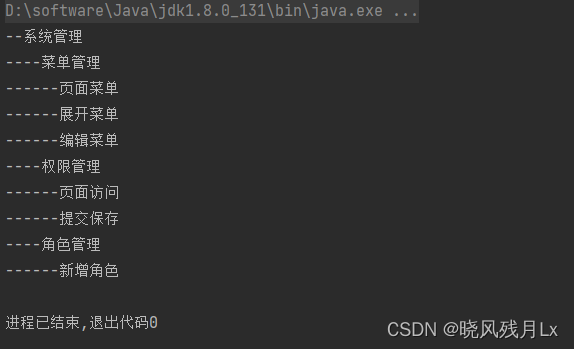
Gof23设计模式之组合模式
1.定义 组合模式又名部分整体模式,是用于把一组相似的对象当作一个单一的对象。组合模式依据树形结构来组合对象,用来表示部分以及整体层次。这种类型的设计模式属于结构型模式,它创建了对象组的树形结构。 2.结构 组合模式主要包含三种…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
