P1194 买礼物(最小生成树)(内附封面)
买礼物
题目描述
又到了一年一度的明明生日了,明明想要买 B B B 样东西,巧的是,这 B B B 样东西价格都是 A A A 元。
但是,商店老板说最近有促销活动,也就是:
如果你买了第 I I I 样东西,再买第 J J J 样,那么就可以只花 K I , J K_{I,J} KI,J 元,更巧的是, K I , J K_{I,J} KI,J 竟然等于 K J , I K_{J,I} KJ,I。
现在明明想知道,他最少要花多少钱。
输入格式
第一行两个整数, A , B A,B A,B。
接下来 B B B 行,每行 B B B 个数,第 I I I 行第 J J J 个为 K I , J K_{I,J} KI,J。
我们保证 K I , J = K J , I K_{I,J}=K_{J,I} KI,J=KJ,I 并且 K I , I = 0 K_{I,I}=0 KI,I=0。
特别的,如果 K I , J = 0 K_{I,J}=0 KI,J=0,那么表示这两样东西之间不会导致优惠。
输出格式
一个整数,为最小要花的钱数。
样例 #1
样例输入 #1
1 1
0
样例输出 #1
1
样例 #2
样例输入 #2
3 3
0 2 4
2 0 2
4 2 0
样例输出 #2
7
提示
样例解释 2 2 2。
先买第 2 2 2 样东西,花费 3 3 3 元,接下来因为优惠,买 1 , 3 1,3 1,3 样都只要 2 2 2 元,共 7 7 7 元。
(同时满足多个“优惠”的时候,聪明的明明当然不会选择用 4 4 4 元买剩下那件,而选择用 2 2 2 元。)
数据规模
对于 30 % 30\% 30% 的数据, 1 ≤ B ≤ 10 1\le B\le 10 1≤B≤10。
对于 100 % 100\% 100% 的数据, 1 ≤ B ≤ 500 , 0 ≤ A , K I , J ≤ 1000 1\le B\le500,0\le A,K_{I,J}\le1000 1≤B≤500,0≤A,KI,J≤1000。
2018.7.25新添数据一组
大致思路
简单的最小生成树问题
对于这种问题,关键是如何把题目转化为使用最小生成树解决。
对于本题,注意每个物品有自己的初始价格与优惠价格
但是!也有反向优惠(优惠了还不如不优惠)的情况
那么我们需要选择所有物品,而物品之间有优惠关系,可以把每个物品看做一个点,每个优惠看作一条边权为 w 的边,那么这个问题也就转化为了最小生成树问题
对于上述的反向优惠的情况,我们可以建一个超级点 ‘0’,向每一个点建一条边权为 a 的边,这样就可以避免反向优惠的情况啦~
AC CODE
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+114514;
int a,n,ans=0;
int sum=0,fa[N];
struct node{int u,v,w;
}k[N];
bool cmp(node aa,node bb){return aa.w<bb.w;
}
int find(int x){if(fa[x]==x)return x;return fa[x]=find(fa[x]);
}
void merge(int x,int y){fa[find(x)]=find(y);
}
void kruskal(){sort(k+1,k+1+sum+n+1,cmp);for(int i=1;i<=n;i++){fa[i]=i;}for(int i=1;i<=sum+n+1;i++){if(find(k[i].u)!=find(k[i].v)){ans+=k[i].w;merge(k[i].u,k[i].v);}}
}
int main(){cin>>a>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){int w;cin>>w;if(w==0)continue;sum++;k[sum].u=i;k[sum].v=j;k[sum].w=w;}}for(int i=sum+1;i<=sum+n;i++){k[i].u=0;k[i].v=i-sum;k[i].w=a;}kruskal();cout<<ans<<endl;return 0;
}
附封面(天气之子)

相关文章:

P1194 买礼物(最小生成树)(内附封面)
买礼物 题目描述 又到了一年一度的明明生日了,明明想要买 B B B 样东西,巧的是,这 B B B 样东西价格都是 A A A 元。 但是,商店老板说最近有促销活动,也就是: 如果你买了第 I I I 样东西࿰…...

oracle基础语法和备份恢复
Oracle总结 sql命令分类 1.DDL,数据定义语言,create创建/drop销毁 2.DCL,数据库控制语言,grant授权/revoke撤销 3.DML,数据操纵语言,insert/update/delete等sql语句 4.DQL,数据查询语言&am…...

【MATLAB第66期】#源码分享 | 基于MATLAB的PAWN全局敏感性分析模型(有条件参数和无条件参数)
【MATLAB第66期】#源码分享 | 基于MATLAB的PAWN全局敏感性分析模型(有条件参数和无条件参数) 文献参考 Pianosi, F., Wagener, T., 2015. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions.…...

vue2过渡vue3技术差异点指南
基础点 reactive() 定义响应式变量(仅仅引用类型有效:对象数组map,set):reactive(),类似于data中return的数据 例子: import { reactive } from vueexport default {setup() {const state reactive({ count: 0 })function in…...
两个多选框(select)之间值的左右上下移动
<!DOCTYPE html> <html> <head><meta charset"utf-8"><title>两个多选框(select)之间值的左右上下移动</title> </head> <script src"https://cdn.bootcss.com/jquery/3.3.1/jquery.js"></script>&…...

【设计模式】——模板模式
什么是模板模式? 模板方法模式(Template Method Pattern),又叫模板模式(Template Pattern),在一个抽象类公开定义了执行它的方法的模板。它的子类可以按需要重写方法实现,但调用将以抽象类中定义的方式进行…...
工业机器视觉系统开发流程简介
需求分析和系统设计:与用户合作,明确系统的功能和性能需求,并设计系统的整体架构。 软、硬件选型:根据需求分析结果,选择适合的软、硬件设备,包括光学传感器、相机、光源、图像采集设备、处理器等。 软件…...

【Unity3D】Renderer Feature简介
1 3D 项目迁移到 URP 项目后出现的问题 3D 项目迁移至 URP 项目后,会出现很多渲染问题,如:材质显示异常、GL 渲染不显示、多 Pass 渲染异常、屏幕后处理异常等问题。下面将针对这些问题给出一些简单的解决方案。 URP 官方教程和 API 详见→Un…...
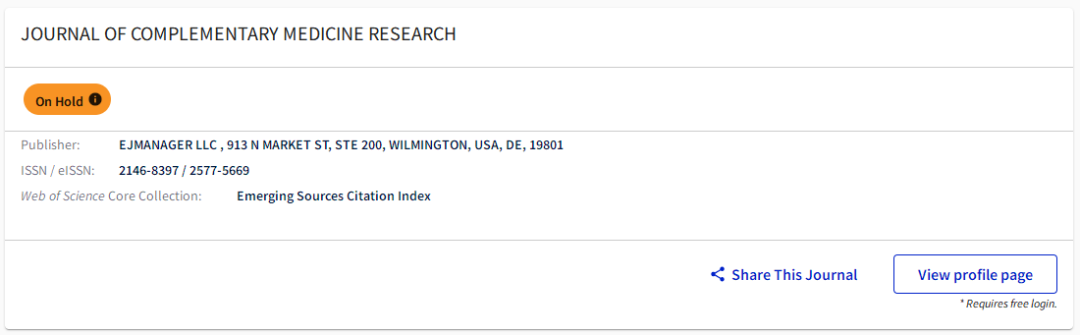
麻了!包含中科院TOP,共16本期刊被标记为“On Hold”状态!
近日,小编从科睿唯安旗下的“Master Journal List”官网查到,除了知名老牌期刊Chemosphere竟然被标记为“On Hold”状态,目前共有7本SCI期刊,1本SSCI期刊,8本ESCI期刊被标记为“On Hold”,究竟是怎么回事呢…...

2.Flink应用
2.1 数据流 DataStream:DataStream是Flink数据流的核心抽象,其上定义了对数据流的一系列操作DataStreamSource:DataStreamSource 是 DataStream 的 起 点 , DataStreamSource 在StreamExecutionEnvironment 中 创 建 ,…...
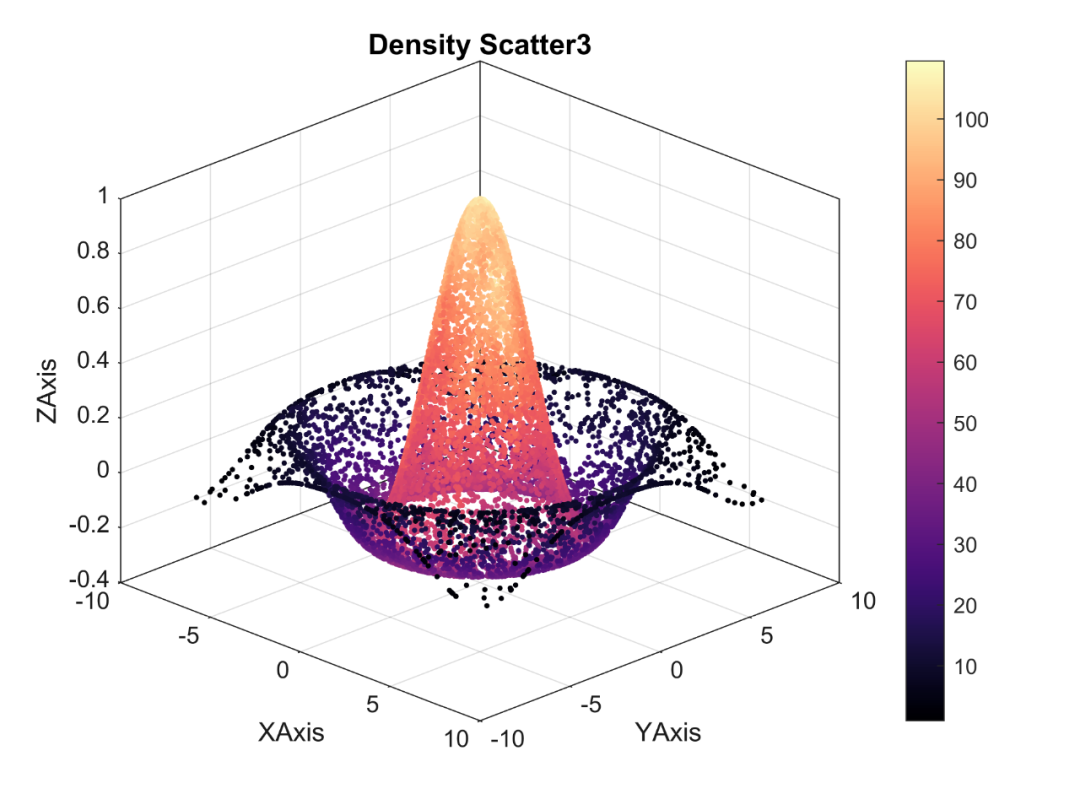
Matlab进阶绘图第25期—三维密度散点图
三维密度散点图本质上是一种特征渲染的三维散点图,其颜色表示某一点所在区域的密度信息。 除了作图,三维密度散点图绘制的关键还在于密度的计算。 当然,不管是作图还是密度的计算,这些在《Matlab论文插图绘制模板》和《Matlab点…...

C++设计模式之桥接设计模式
文章目录 C桥接设计模式什么是桥接设计模式该模式有什么优缺点优点缺点 如何使用 C桥接设计模式 什么是桥接设计模式 桥接设计模式是一种结构型设计模式,它可以将抽象接口和实现分离开来,以便它们可以独立地变化和扩展。 该模式有什么优缺点 优点 灵…...
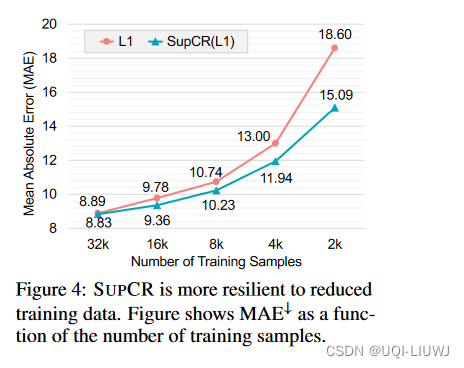
论文笔记:SUPERVISED CONTRASTIVE REGRESSION
2022arxiv的论文,没有中,但一作是P大图班本MIT博,可信度应该还是可以的 0 摘要 深度回归模型通常以端到端的方式进行学习,不明确尝试学习具有回归意识的表示。 它们的表示往往是分散的,未能捕捉回归任务的连续性质。…...

Java 多线程并发 CAS 技术详解
一、CAS概念和应用背景 CAS的作用和用途 CAS(Compare and Swap)是一种并发编程中常用的技术,用于解决多线程环境下的并发访问问题。CAS操作是一种原子操作,它可以提供线程安全性,避免了使用传统锁机制所带来的性能开…...
如何压缩高清PDF文件大小?将PDF文件压缩到最小的三个方法
PDF格式是一种非常常用的文档格式,但是有时候我们需要将PDF文件压缩为更小的大小以便于传输和存储。在本文中,我们将介绍三种PDF压缩的方法,包括在线PDF压缩、利用软件PDF压缩以及使用WPS缩小pdf。 首先,在线PDF压缩是最常用的方…...
)
04 统计语言模型(n元语言模型)
博客配套视频链接: https://space.bilibili.com/383551518?spm_id_from=333.1007.0.0 b 站直接看 配套 github 链接:https://github.com/nickchen121/Pre-training-language-model 配套博客链接:https://www.cnblogs.com/nickchen121/p/15105048.html 预训练 预先训练 我们…...

Linux各目录详解
Linux文件系统是一个树状结构,由多个目录(或文件夹)组成。以下是常见的Linux目录及其功能的详细解释: /(根目录):在Linux文件系统中,所有其他目录和文件都是从根目录派生的。所有的存…...

【css】属性选择器分类
属性选择器类型示例说明[attribute][target]选择带有 target 属性的所有元素[attributevalue][target_blank]选择带有 target“_blank” 属性的所有元素[attribute~value][title~flower]选择带有包含 “flower” 一词的 title 属性的所有元素[attribute|value][lang|en]选择带有…...

备份容灾哪家好怎么样
数字化时代,数据安全是我们不容忽视的问题。云呐容灾备份系统不仅提供了强大的数据保护功能,而且操作简单,使用方便。无论你是企业管理员,还是个人用户,都可以轻松上手。它还提供了丰富的报告和监控功能,让…...
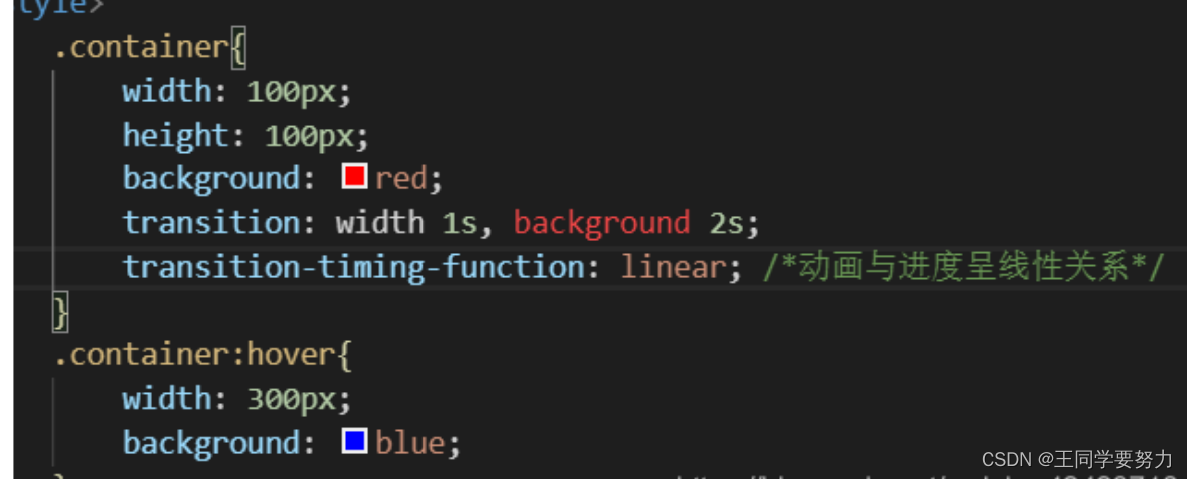
【前端实习生备战秋招】—HTML 和 CSS面试题总结(三)
【前端实习生备战秋招】—HTML 和 CSS面试题总结(三) 1.行内元素有哪些?块级元素有哪些? 空(void)元素有那些? CSS 规范规定,每个元素都有 display 属性,确定该元素的类型,每个元素…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
