备战秋招012(20230808)
文章目录
- 前言
- 一、今天学习了什么?
- 二、动态规划
- 1.概念
- 2.题目
- 总结
前言
提示:这里为每天自己的学习内容心情总结;
Learn By Doing,Now or Never,Writing is organized thinking.
提示:以下是本篇文章正文内容
一、今天学习了什么?
- 学习了代码随想录关于动态规划的算法;
- 还有01背包问题
二、动态规划
1.概念
「动态规划」(Dynamic Programming),适用于很多重叠子问题的场景**,每一个结果一定是由于上一个状态推导出来的,选择和状态转移**。解题步骤如下:
- 确定dp数组(dp table)以及下标的含义;
- 确定递推公式;
- dp数组如何初始化;
- 确定遍历顺序;
- 举例推导dp数组;
「01 背包问题」是指,有 n 个物品和一个最多能背负 w 重量的背包,求该背包能背负的最大重量。第 i 个物品的重量为 weight[i] ,价值为 value[i] 。
有两种解法:
- 二维数组:
- dp[i] [j] ,表示从下标为 [0,i] 的物品中,放进背包容量为 j 时的最大价值;
- 确定遍历的顺序,先遍历背包容量,再去逐个遍历物品个数;
- 一维数组:
- dp[i] ,表示背包容量为 i 时的背包最大价值;
- 先遍历物品,再去遍历背包容量,并且保证遍历背包容量时是从大到小的,保证物品只会被放入了一次。
/*** - 采用二维数组解决背包问题* - 只有当当前背包的容量能放下当前物品的重量时,才需要去判断是否需要将物品放入背包中* - 按照先遍历物品,再去遍历背包容量的顺序执行*/public static int testWeightBagProblem01(int[] weight, int[] value, int bagSize) {int m = weight.length;int[][] dp = new int[m][bagSize + 1];for (int j = weight[0]; j <= bagSize; j++) {dp[0][j] = value[0];}for (int j = 1; j <= bagSize; j++) {for (int i = 1; i < m; i++) {if (j >= weight[i]) {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);} else {dp[i][j] = dp[i - 1][j];}}}return dp[m - 1][bagSize];}/*** - 一维数组* - 背包容量的最大值取决于之前背包容量更小时候的最大值*/public static int testWeightBagProblem02(int[] weight, int[] value, int bagSize) {int[] dp = new int[bagSize + 1];for (int i = 0; i < weight.length; i++) {// 先遍历物品for (int j = bagSize; j >= weight[i]; j--) {// 再去遍历背包容量// 判断将此物品放入背包的结果dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); //不放、放}}return dp[bagSize];}
2.题目
- 509. 斐波那契数
public int fib(int n) {if (n == 0 || n == 1) {return n;}/*** 动态规划* - dp数组* - 选择* - 状态转移* dp[i] 代表f(n)*/int[] dp = new int[n + 3];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
- 70. 爬楼梯
public int climbStairs(int n) {if (n == 1 || n == 2) {return n;}/*** 遇到重叠子问题,采用动态规划* - dp数组含义:dp[i]表示有dp[i]种方法可以爬到楼顶(楼顶的台阶数为i)* - 初始化* - 状态转移和选择*/int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
- 746. 使用最小花费爬楼梯
public int minCostClimbingStairs(int[] cost) {/*** - 采用动态规划* - dp[i]:爬上i层使用的最少的花费*/int[] dp = new int[cost.length + 1];for (int i = 2; i <= cost.length; i++) {dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[cost.length];}
- 62. 不同路径
public int uniquePaths(int m, int n) {/*** - 每次都需要选择,采用动态规划* - dp[i][j]:到达(i,j)点的路径*/int[][] dp = new int[m][n];for (int i = 0; i < m; i++) {dp[i][0] = 1;}for (int j = 0; j < n; j++) {dp[0][j] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
- 63. 不同路径 II
public int uniquePathsWithObstacles(int[][] obstacleGrid) {/*** 还是使用动态规划,只不过需要判断是否可达*/int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];for (int i = 0; i < m; i++) {if (obstacleGrid[i][0] == 1) {break;}dp[i][0] = 1;}for (int j = 0; j < n; j++) {if (obstacleGrid[0][j] == 1) {break;}dp[0][j] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) {continue;}dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
- 343. 整数拆分
public int integerBreak(int n) {if (n <= 3) {return n - 1;}/*** - 如何使用动态规划呢?* - 就需要从怎么拆入手* - 是否要拆,取决于拆完后结果和之前的结果谁更大*/int[] dp = new int[n + 1];dp[2] = 1;for (int i = 3; i <= n; i++) {for (int j = 1; j <= i - j; j++) {dp[i] = Math.max(dp[i], Math.max((i - j) * j, dp[i - j] * j));}}return dp[n];}public int integerBreak2(int n) {if (n <= 3) {return n - 1;}/*** - 这是纯数学解答* - 任何整数都可以拆成2和3* - 怎么拆,取决于模上3的余数是多少*/int remainder = n % 3;int times = n / 3;if (remainder == 0) {return (int) Math.pow(3, times);} else if (remainder == 1) {return (int) Math.pow(3, times - 1) * 4;} else {return (int) Math.pow(3, times) * 2;}}
- 96. 不同的二叉搜索树(⭐⭐⭐⭐⭐)
这个题有点难,在于如何的合适区拆分成子问题:
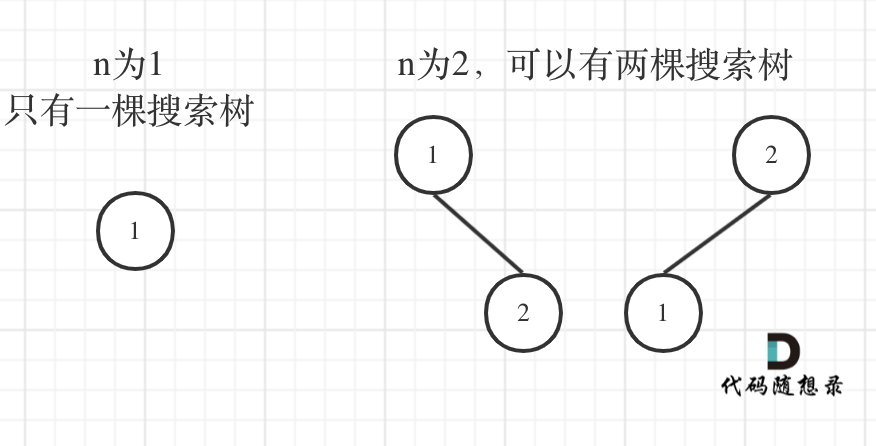
应该先举几个例子,画画图,看看有没有什么规律,如图:
- 当
n = 1 , 2时都很直观; - 当
n = 3时,分为:- 当1为头结点的时候,其右子树有两个节点,看这两个节点的布局,是不是和 n 为2的时候两棵树的布局是一样的啊!
- 当2为头结点的时候,其左右子树都只有一个节点,布局是不是和n为1的时候只有一棵树的布局也是一样的啊!
- 当3为头结点的时候,其左子树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是一样的啊!
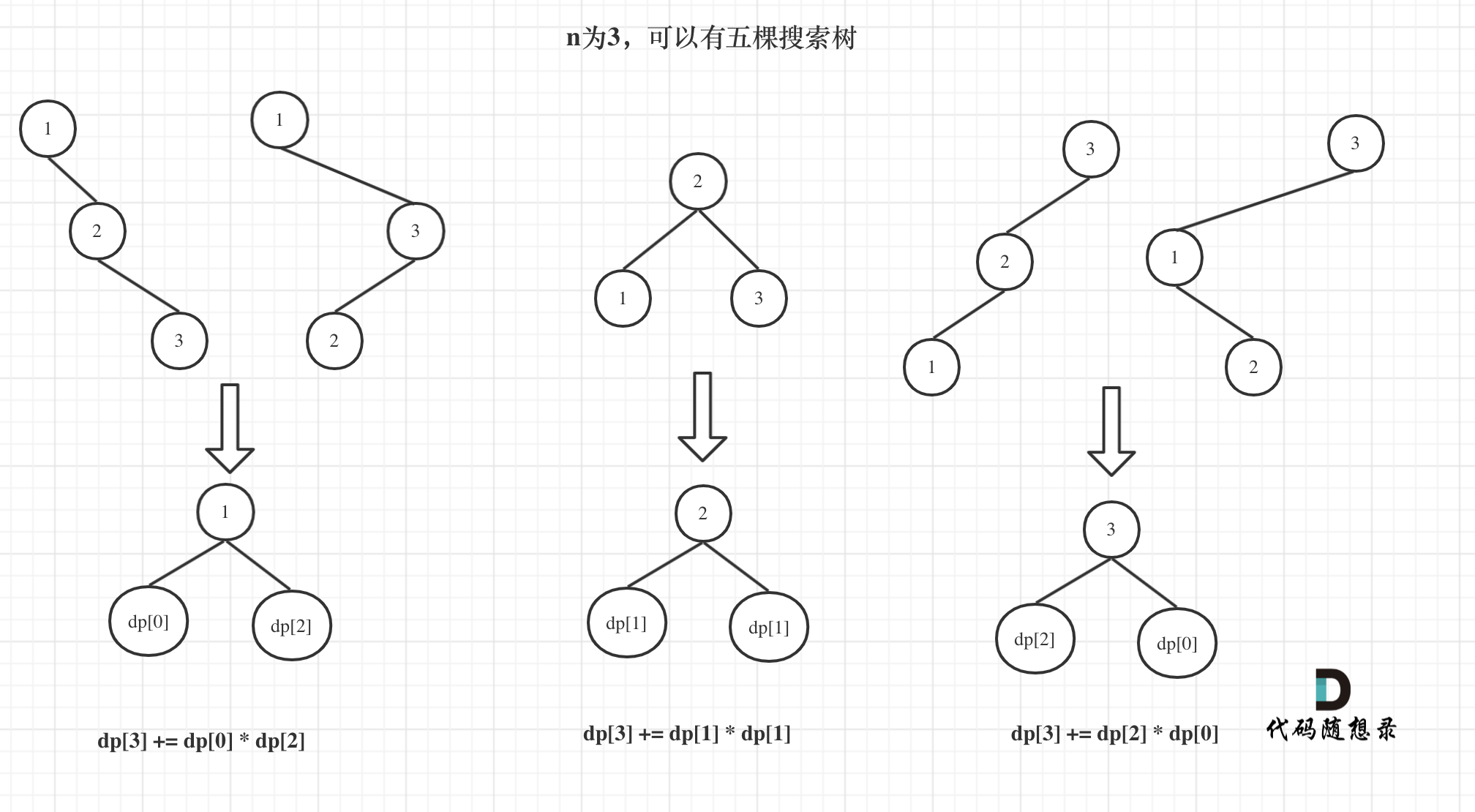
- dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量;
- dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2];
- 元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量;
- 元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量;
- 元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量;
public int numTrees(int n) {/*** - 这个题有点难,在于如何正确的处理拆分子问题* - dp[i],代表i个节点组成的二叉搜索树的种数* - 拆分为 1.2.3.....i 为头节点组成的二叉搜索树的之和就是i个节点组成的二叉搜索树的种数*/int[] dp = new int[n + 1];dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[i - j] * dp[j - 1];}}return dp[n];}
- 416. 分割等和子集(⭐⭐⭐)
public boolean canPartition(int[] nums) {/*** - 可以将问题看成,是否能将数组中的元素凑出数组元素和的一半* - 背包容量为一半的数组和,物品价值和物品重量都是nums数组* - 采用一维数组的话,dp[i]代表数组容量为i时能背的最大价值*/int sum = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];}if (sum % 2 != 0) {return false;}sum /= 2;int[] dp = new int[sum + 1];for (int i = nums[0]; i <= sum; i++) {dp[i] = nums[0];}for (int i = 1; i < nums.length; i++) {for (int j = sum; j >= nums[i]; j--) {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}}return dp[sum] == sum;}
- 1049. 最后一块石头的重量 II
public int lastStoneWeightII(int[] stones) {/*** - 也是背包问题*/int sum = 0;for (int i = 0; i < stones.length; i++) {sum += stones[i];}int target = sum / 2;int[] dp = new int[target + 1];for (int i = stones[0]; i <= target; i++) {dp[i] = stones[0];}for (int i = 1; i < stones.length; i++) {for (int j = target; j >= stones[i]; j--) {dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
总结
提示:这里对文章进行总结:
今天效率一般,心情有点emo,很害怕。
相关文章:

备战秋招012(20230808)
文章目录 前言一、今天学习了什么?二、动态规划1.概念2.题目 总结 前言 提示:这里为每天自己的学习内容心情总结; Learn By Doing,Now or Never,Writing is organized thinking. 提示:以下是本篇文章正文…...

QT中定时器的使用
文章目录 概述步骤 概述 Qt中使用定时器大致有两种,本篇暂时仅描述使用QTimer实现定时器 步骤 // 1.创建定时器对象 QTimer *timer new QTimer(this);// 2.开启一个定时器,5秒触发一次 timer->start(5000); // 3.建立信号槽连接&am…...
【UE4】多人联机教程(重点笔记)
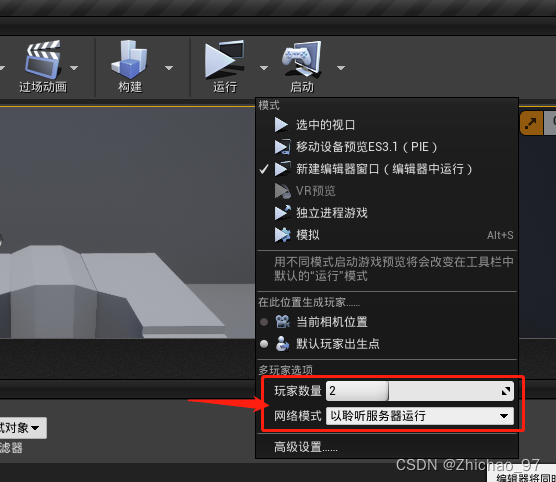
效果 1. 创建房间、搜索房间功能 2. 根据指定IP和端口加入游戏 步骤 1. 新建一个第三人称角色模板工程 2. 创建一个空白关卡,这里命名为“InitMap” 3. 新建一个控件蓝图,这里命名为“UMG_ConnectMenu” 在关卡蓝图中显示该控件蓝图 打开“UMG_Connec…...

【go】GIN参数重复绑定报错EOF问题
文章目录 1 问题描述2 解决:替换为ShouldBindBodyWith 1 问题描述 在 Gin 框架中,当多次调用 ShouldBind() 或 ShouldBindJSON() 方法时,会导致请求体的数据流被读取多次,从而出现 “EOF” 错误。 例如在api层绑定了参数&#x…...
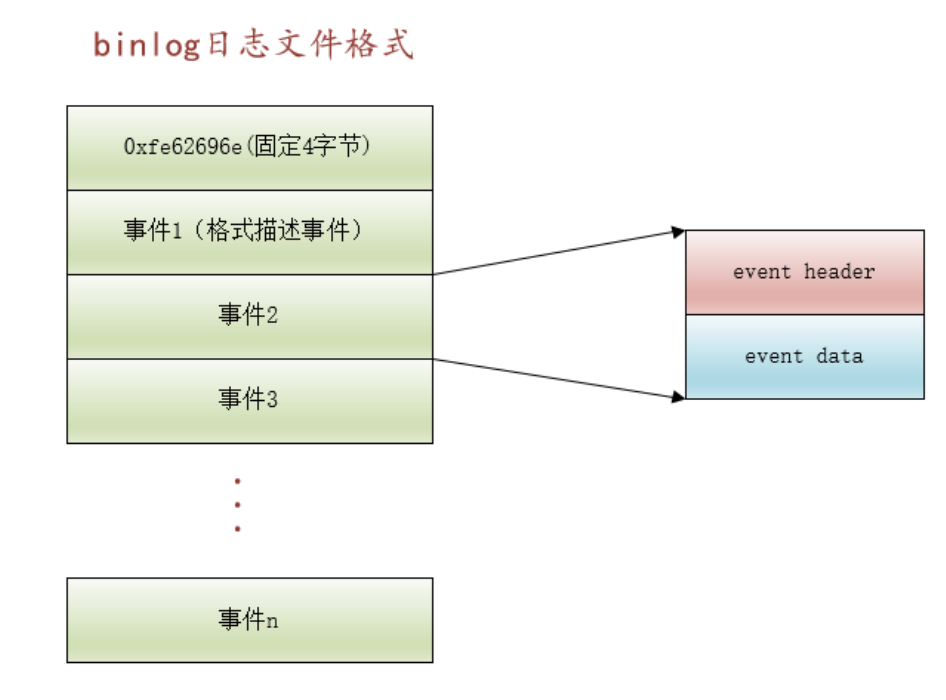
关于MySQL中的binlog
介绍 undo log 和 redo log是由Inno DB存储引擎生成的。 在MySQL服务器架构中,分为三层:连接层、服务层(server层)、执行层(存储引擎层) bin log 是 binary log的缩写,即二进制日志。 MySQL…...

我维护电脑的方法
无论是学习还是工作,电脑都是IT人必不可少的重要武器,一台好电脑除了自身配置要经得起考验,后期主人对它的维护也是决定它寿命的重要因素! 你日常是怎么维护你的“战友”的呢,维护电脑运行你有什么好的建议吗ÿ…...
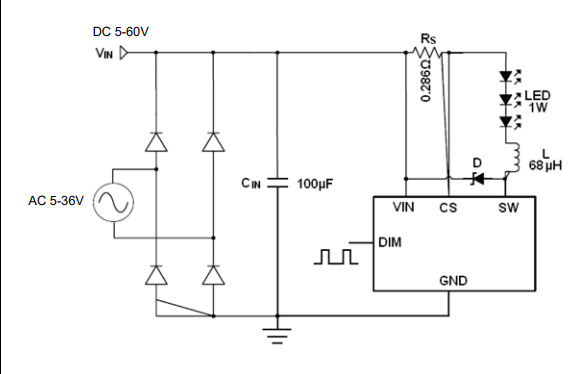
AP51656 电流采样降压恒流驱动IC RGB PWM深度调光 LED电源驱动
产品描述 AP51656是一款连续电感电流导通模式的降压恒流源,用于驱动一颗或多颗串联LED 输入电压范围从 5 V 到 60V,输出电流 可达 1.5A 。根据不同的输入电压和 外部器件, 可以驱动高达数十瓦的 LED。 内置功率开关,采用电流采样…...
Python爬虫的解析(学习于b站尚硅谷)
目录 一、xpath 1.xpath插件的安装 2. xpath的基本使用 (1)xpath的使用方法与基本语法(路径查询、谓词查询、内容查询(使用text查看标签内容)、属性查询、模糊查询、逻辑运算) (2&a…...
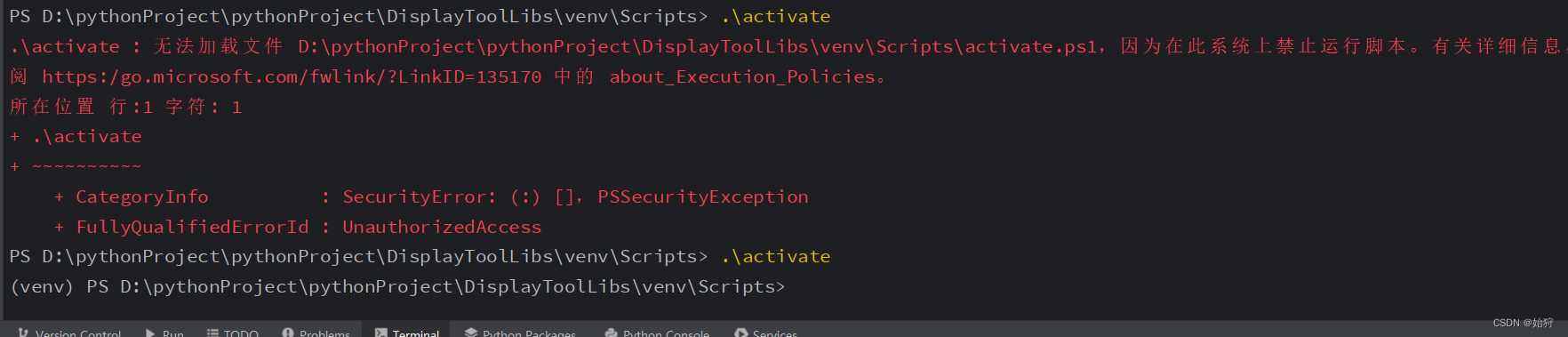
python的virtualenv虚拟环境无法激活activate
目录 问题描述: 解决办法: 解决结果: 问题描述: PS D:\pythonProject\pythonProject\DisplayToolLibs\venv\Scripts> .\activate .\activate : 无法加载文件 D:\pythonProject\pythonProject\DisplayToolLibs\venv\Scripts\…...

uniapp中token操作:存储、获取、失效处理。
实现代码 存储token:uni.setStorageSync(token, res.data.result);获取token:uni.getStorageSync(token);清除token:uni.setStorageSync(token, ); 应用场景 在登录操作中,保存token pwdLogin() {....this.$axios.request({url: .....,method: post,p…...

乐鑫科技 2022 笔试面试题
岗位:嵌入式软件实习生。 个人情况:本科双非电子信息工程,硕士华五软件工程研一在读;本科做过一些很水的项目 ,也拿项目搞了一些奖,相对来说嵌入式方向比较对口。 时间线及面试流程 2021.04.02 笔试 题目分为选择题和编程题,选择题二十题,编程题两题; 选择题基本…...
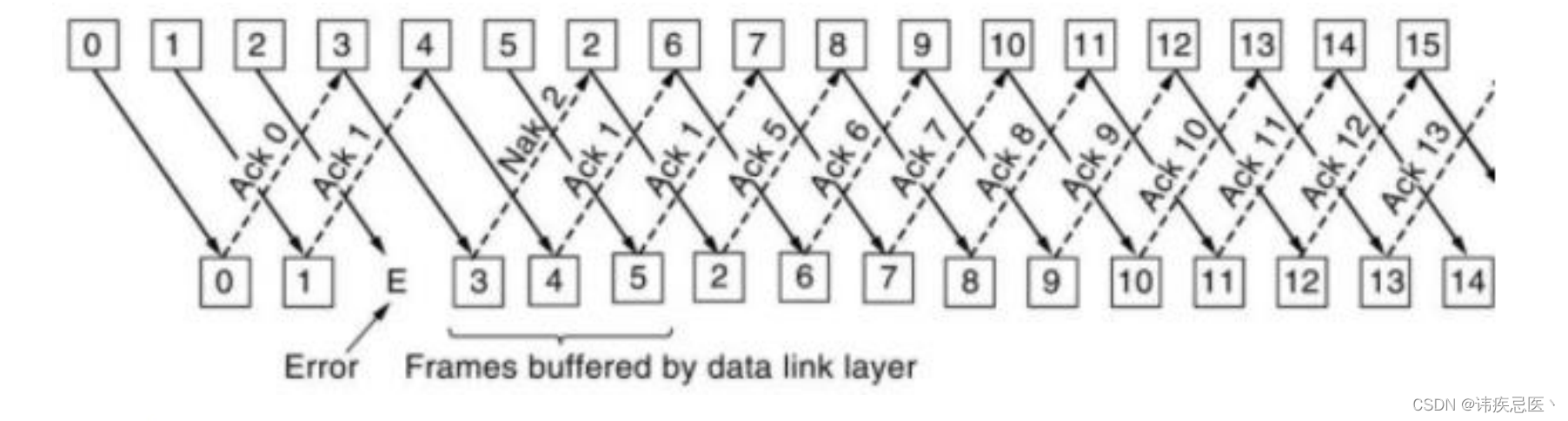
实现UDP可靠性传输
文章目录 1、TCP协议介绍1.1、ARQ协议1.2、停等式1.3、回退n帧1.4、选择性重传 1、TCP协议介绍 TCP协议是基于IP协议,面向连接,可靠基于字节流的传输层协议 1、基于IP协议:TCP协议是基于IP协议之上传输的,TCP协议报文中的源端口IP…...

Zebec Protocol 将进军尼泊尔市场,通过 Zebec Card 推动地区金融平等
流支付正在成为一种全新的支付形态,Zebec Protocol 作为流支付的主要推崇者,正在积极的推动该支付方案向更广泛的应用场景拓展。目前,Zebec Protocol 成功的将流支付应用在薪酬支付领域,并通过收购 WageLink 将其纳入旗下…...

Qt--动态链接库的创建和使用
写在前面 在Qt的实际开发中,免不了使用和创建动态链接库,因此熟悉Qt中动态链接库的创建和使用对后续的库开发或使用是非常用必要的。 在之前的文章https://blog.csdn.net/SNAKEpc12138/article/details/126189926?spm1001.2014.3001.5501中已经对导入…...
)
设计模式十二:享元模式(Flyweight Pattern)
当我们需要创建大量相似对象时,享元模式可以帮助我们节省内存空间和提高性能。该模式通过共享相同的数据来减少对象的数量。 在享元模式中,有两种类型的对象:享元(Flyweight)和非享元(Unshared Flyweight&a…...

【LeetCode】88. 合并两个有序数组 - 双指针
这里写自定义目录标题 2023-8-7 22:35:41 88. 合并两个有序数组 双指针 2023-8-7 22:35:41 class Solution {public void merge(int[] nums1, int m, int[] nums2, int n) {int last m n ;while(n > 0){if(m > 0 && nums2[n-1] > nums1[m-1]){nums1[las…...

HarmonyOS应用开发的新机遇与挑战
HarmonyOS 4已经于2023年8月4日在HDC2023大会上正式官宣。对广大HarmonyOS开发者而言,这次一次盛大的大会。截至目前,鸿蒙生态设备已达7亿台,HarmonyOS开发者人数超过220万。鸿蒙生态充满着新机遇,也必将带来新的挑战。 HarmonyO…...

Qt中qmake、构建、运行、清理的区别
Qt 中默认的执行顺序:qmake--- 编译 --- 运行。 一、qmake qmake: 根据之前项目指南创建的项目文件 .pro,并且运行 qmake [qmake xx.pro]生成调试 [build-ttt-***-Debug] 或者发布 [build-ttt-***-Release] 目录(这个是影子构建…...

【设计模式——学习笔记】23种设计模式——观察者模式Observer(原理讲解+应用场景介绍+案例介绍+Java代码实现)
文章目录 案例引入原始方案实现实现问题分析 介绍基础介绍登场角色 案例实现案例一类图实现分析 案例二类图实现 观察者模式在JDK源码的应用总结文章说明 案例引入 有一个天气预报项目,需求如下: 气象站可以将每天测量到的温度、湿度、气压等等以公告的…...

【奇葩瑞萨-004】RX系列单片机的GPIO初始化
RX系列单片机的GPIO初始化 与IO口相关的寄存器端口(PORT)寄存器端口功能控制(MPC)寄存器MPC.PmnFPS的设置过程MPC寄存器设置注意事项 端口Pmn的初始化不同端口模式下,PORT、MCP寄存器的配置顺序 感想:与STM…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
