[LeetCode]1237. 找出给定方程的正整数解
题目链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/
题目描述:
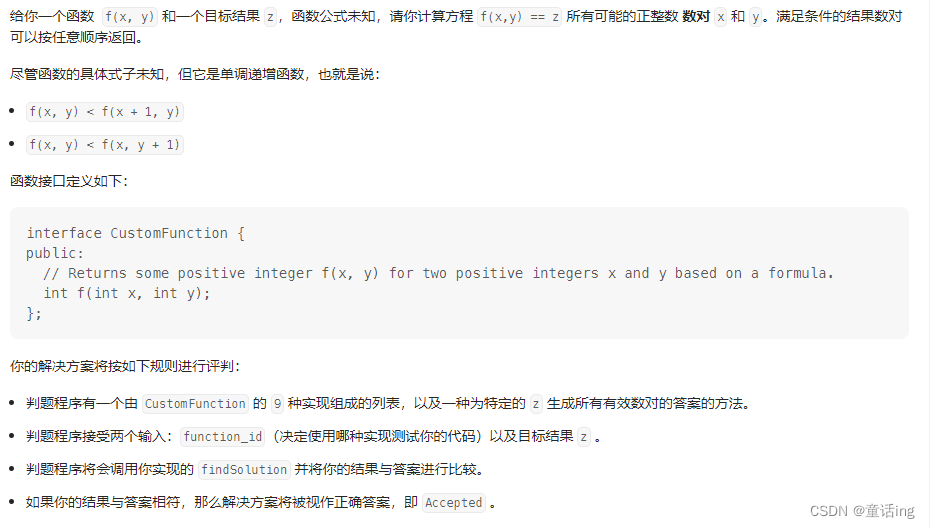
样例1:
输入:function_id = 1, z = 5
输出:[[1,4],[2,3],[3,2],[4,1]]
解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5
样例2:
输入:function_id = 2, z = 5
输出:[[1,5],[5,1]]
解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5
题目限定:

方法1:暴力枚举
func findSolution(customFunction func(int, int) int, z int) [][]int {res := make([][]int, 0, 100)for x := 1; x <= 1000; x++ {for y := 1; y<= 1000; y++ {if customFunction(x,y) == z {temp := []int{x, y}res = append(res,temp)}}}return res
}
暴力枚举法每次都从开始找y,x最多枚举1000次,而y每次也会枚举1000次,因此,总的复杂度为O(x*y)。
方法2:枚举+二分查找
func findSolution(customFunction func(int, int) int, z int) (res [][]int) {for x := 1; x <= 1000; x++ {l, r := 1, 1000for l <= r {mid := (l+r)/2if customFunction(x,mid) == z {res = append(res, []int{x,mid})break} else if customFunction(x,mid) > z {r = mid -1 } else {l = mid + 1}}}return res
}
既然我们知道y每次都从头开始找比较慢,那么我们可以优化y的查找时间,利用二分查找即可将找y的复杂度降到log级别,因此总的时间复杂度为O(xlogy)。
当然,golang中也可以使用sort库的Search方法:
func findSolution(customFunction func(int, int) int, z int) (res [][]int) {for x := 1; x <= 1000; x++ {y := 1 + sort.Search(999, func(y int) bool {return customFunction(x, y+1) >= z})if customFunction(x,y) == z {res = append(res, []int{x,y})}}return res
}
同时需要注意Search的用法,是从[0,n)去查找的,所以类似我们是从0-999中查找出来的下标,最后加上1就表示从1到1000了:
// Search uses binary search to find and return the smallest index i
// in [0, n) at which f(i) is true, assuming that on the range [0, n),
// f(i) == true implies f(i+1) == true. That is, Search requires that
// f is false for some (possibly empty) prefix of the input range [0, n)
// and then true for the (possibly empty) remainder; Search returns
// the first true index. If there is no such index, Search returns n.
// (Note that the “not found” return value is not -1 as in, for instance,
方法3:双指针
func findSolution(customFunction func(int, int) int, z int) (res [][]int) {y := 1000for x := 1; x <= 1000; x++ {for ; y > 0 ; y-- {if customFunction(x,y) < z {break}if customFunction(x,y) == z {res = append(res, []int{x,y})break}}}return res
}
这种方法关键在于直接利用函数单调递增的特性,一个答案从前往后找,另一个答案从后往前找,下一次寻找一定是基于上一次的结果,因此会少很多次遍历,x最多遍历1000次,y总的遍历次数也最多1000次,因此总的时间复杂度为O(x+y)。
相关文章:

[LeetCode]1237. 找出给定方程的正整数解
题目链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/ 题目描述: 样例1: 输入:function_id 1, z 5 输出:[[1,4],[2,3],[3,2],[4,1]] 解释:functi…...

【路径规划】基于A*算法和Dijkstra算法的路径规划(Python代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

蓝桥杯 stm32 PWM 设置占空比
本文代码使用 HAL 库。 文章目录 前言一、创建CubeMX 工程 ,占空比分析:二、相关函数:1. 获取 CNT函数2.设置CNT为 0 函数(计算器清零)3.开启TIM2_CH1的输入捕获中断函数4.TIM 回调函数三、设置上升沿,下降沿四、在lcd上显示 R40 占空比 详细代码五、设置占空比,输出 PW…...
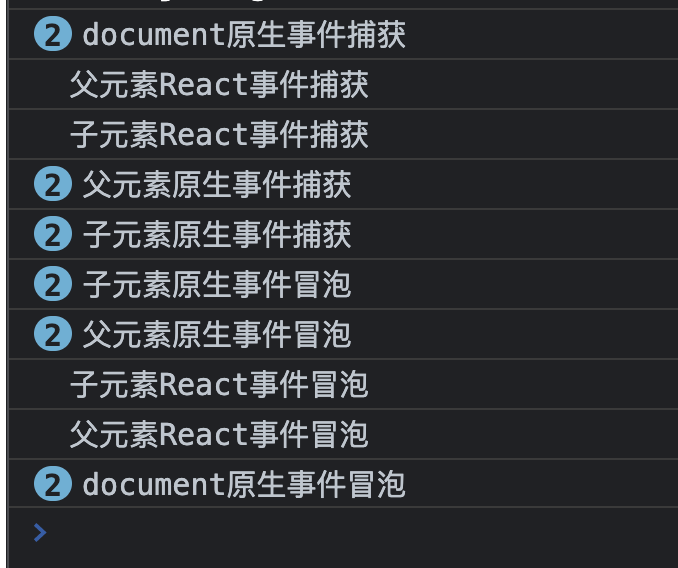
React 合成事件理解
1 事件三个阶段 捕获、目标、处理 (具体百度,后面有空补全)2import React from "react";class Test extends React.Component {parentRef;childRef;constructor(props) {super(props);this.parentRef React.createRef();this.chil…...

202302|读书笔记——国图点滴
杂志剪影|看一本赚一本系列 anywhere 随心而行随心而动,极简相生复古文艺 热情洋溢 色彩斑斓 极致优雅 深邃魅力 新生绽放 灿若星空 异彩纷呈含苞待放 惊艳绽放 爱在云端 空中婚礼 暗夜浪漫 策马逐梦橘影相映 浆果红唇 梦幻无暇 永无止境浮光掠影 微酥清风低调奢华…...

Linux 操作系统原理 — NUMA 架构中的多线程调度开销与性能优化
目录 文章目录 目录前言NUMA 架构中的多线程性能开销1、跨 Node 的 Memory 访问开销2、跨 Core 的多线程 Cache 同步开销3、多线程上下文切换开销4、多线程模式切换开销5、中断处理的开销6、TLB 缓存失效的开销7、内存拷贝的开销NUMA 架构中的性能优化:使用多核编程代替多线程…...
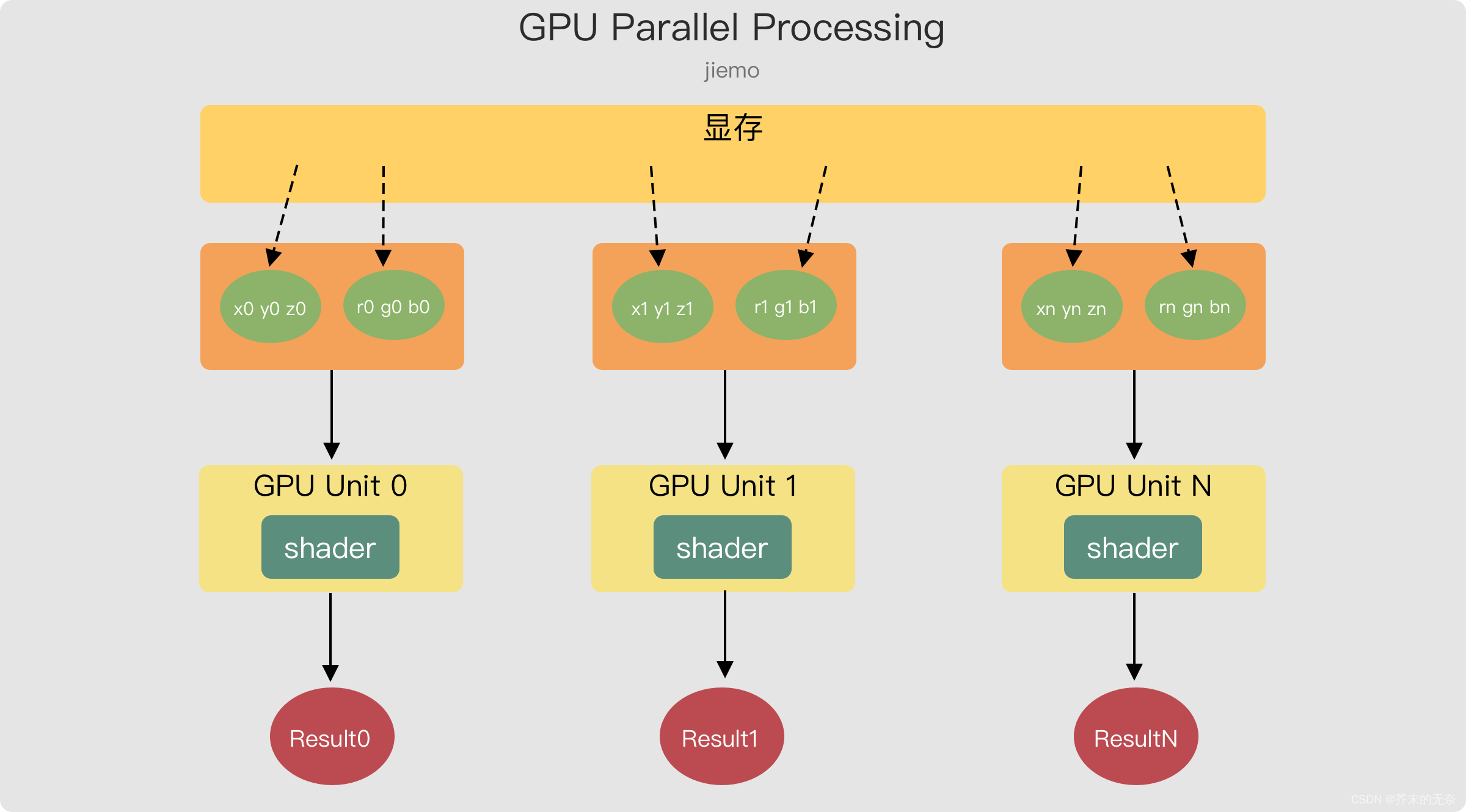
OpenGL - 如何理解 VAO 与 VBO 之间的关系
系列文章目录 LearnOpenGL 笔记 - 入门 01 OpenGLLearnOpenGL 笔记 - 入门 02 创建窗口LearnOpenGL 笔记 - 入门 03 你好,窗口LearnOpenGL 笔记 - 入门 04 你好,三角形 文章目录系列文章目录1. 前言2. 渲染管线的入口 - 顶点着色器2.1 顶点着色器处理过…...

Linux中sed的使用
语法: sed [选项] [sed内置命令字符] [输入文件]选项: 参数说明-n取消默认色的输出常与sed内置命令p一起使用-i直接将修改结果写入文件,不用-i,sed修改的是内存数据-e多次编译,不需要管道符了-r支持正则扩展 sed的内…...
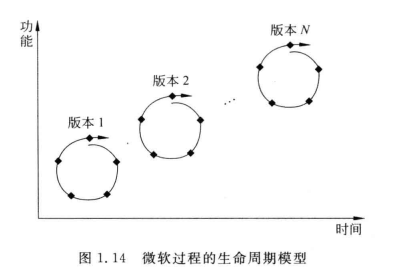
[软件工程导论(第六版)]第1章 软件工程学概述(复习笔记)
文章目录1.1 软件危机1.1.1 软件危机的介绍1.1.2 产生软件危机的原因1.1.3 消除软件危机的途径1.2 软件工程1.2.1 软件工程的介绍1.2.2 软件工程的基本原理1.2.3 软件工程方法学1.3 软件生命周期组成1.4 软件过程概念1.4.1 瀑布模型1.4.2 快速原型模型1.4.3 增量模型1.4.4 螺旋…...

ISP相关
Internet Service Provider,网络提供商/运营商,如电信、联通、移动等。 1. 与ISP互联的出口带宽 IDC或云提供商会与各运营商互联,互联的具体带宽数值一旦泄露,就会被恶意的攻击者利用。例如,若DDos攻击者知道了被攻击…...

vTESTstudio - VT System CAPL Functions - VT2004(续1)
成熟,就是某一个突如其来的时刻,把你的骄傲狠狠的踩到地上,任其开成花或者烂成泥。vtsStartStimulation - 启动激励输出功能:自动激励输出注意:在启动激励输出之前,一定要设置好输出模式Target:目标通道变量空间名称,例…...

WeakMap弱引用
let obj{name:张三} //{name:张三}这个对象能够被读取到,因为obj这个变量名对它的引用 //将引用覆盖掉 objnull //这个对象将会被从内存中移除,因为我们已经失去了对他的所有引用 let obj{name:张三} let arr[obj] objnull //对象{name:张三}不会…...
Springboot 使用quartz 定时任务 增删改查
前段时间公司项目用到了 定时任务 所以写了一篇定时任务的文章 ,浏览量还不错 , Springboot 整合定时任务 ) 所以就准备写第二篇, 如果你是一名Java工程师,你也可以会看到如下的页面 ,去添加定时任务 定时任务展示 :…...
 | 机试题+算法思路 【2023】)
华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】
最近更新的博客 华为OD机试 - 热点网络统计 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 查找单入口空闲区域 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 好朋友 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 找出同班小朋友 | 备考思路,刷题要点…...
Linux常用命令汇总
1、tcpdump抓包 tcpdump这个命令是用来抓包的,默认情况下这个命令是没有的,需要安装一下: yum install -y tcpdump 使用这个命令的时候最好是加上你网卡的名称,不然可能使用不了: tcpdump -nn -i {网卡名称} 网卡名称…...
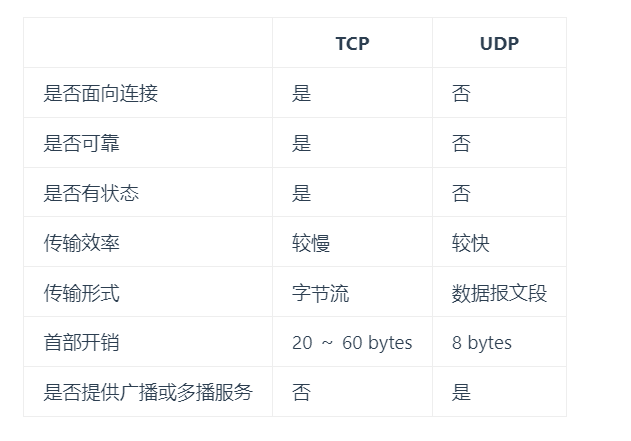
1.TCP、UDP区别、TCP/IP七层、四层模型、应用层协议(计网)
文章目录1.OSI 七层模型是什么?每一层的作用是什么?2.TCP/IP 四层模型是什么?每一层的作用是什么?应用层(Application layer)传输层(Transport layer)网络层(Network lay…...

气敏电阻的原理,结构,分类及应用场景总结
🏡《总目录》 目录 1,概述2,结构3,工作原理4,分类4.1,加热方式分类4.2,材料分类4.3,氧化还原分类5,应用场景6,总结1,概述 气敏电阻是指电阻值随着环境中某种气体的浓度变化而变化的电阻,本文对其工作原理,结构,分类和应用场景进行总结。 2,结构 气敏电阻由防爆…...

实验10 拓扑排序与最短路径2022
A. DS图—图的最短路径(无框架)题目描述给出一个图的邻接矩阵,输入顶点v,用迪杰斯特拉算法求顶点v到其它顶点的最短路径。输入第一行输入t,表示有t个测试实例第二行输入顶点数n和n个顶点信息第三行起,每行输…...

C/C++每日一练(20230218)
目录 1. 整数转罗马数字 2. 跳跃游戏 II 3. 买卖股票的最佳时机 IV 1. 整数转罗马数字 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X …...
【C语言】预编译
🚩write in front🚩 🔎大家好,我是謓泽,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎 🏅2021年度博客之星物联网与嵌入式开发TOP5࿵…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
