算法与数据结构-跳表
文章目录
- 什么是跳表
- 跳表的时间复杂度
- 跳表的空间复杂度
- 如何高效的插入和删除
- 跳表索引动态更新
- 代码示例
什么是跳表
对于一个单链表来讲,即便链表中存储的数据是有序的,如果我们要想在其中查找某个数据,也只能从头到尾遍历链表。这样查找效率就会很低,时间复杂度会很高,是 O(n)。
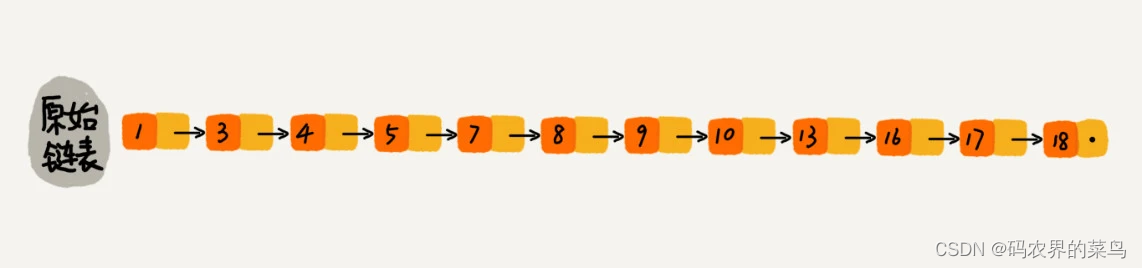
那怎么来提高查找效率呢?如果像图中那样,对链表建立一级“索引”,查找起来是不是就会更快一些呢?每两个结点提取一个结点到上一级,我们把抽出来的那一级叫做索引或索引层。你可以看我画的图。图中的 down 表示 down 指针,指向下一级结点。
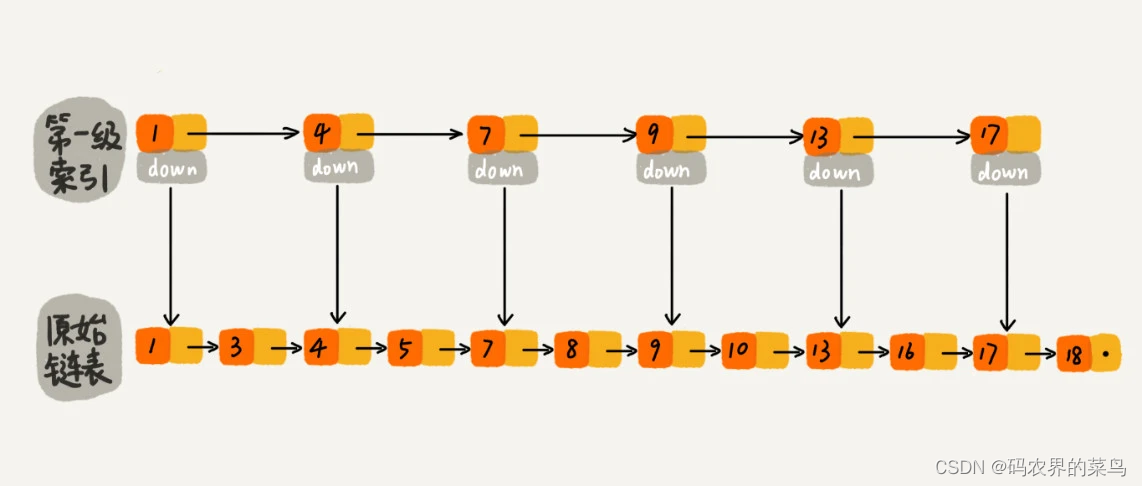
如果我们现在要查找某个结点,比如 16。我们可以先在索引层遍历,当遍历到索引层中值为 13 的结点时,我们发现下一个结点是 17,那要查找的结点 16 肯定就在这两个结点之间。然后我们通过索引层结点的 down 指针,下降到原始链表这一层,继续遍历。这个时候,我们只需要再遍历 2 个结点,就可以找到值等于 16 的这个结点了。这样,原来如果要查找 16,需要遍历 10 个结点,现在只需要遍历 7 个结点。
从这个例子里,我们看出,加来一层索引之后,查找一个结点需要遍历的结点个数减少了,也就是说查找效率提高了。那如果我们再加一级索引呢?效率会不会提升更多呢?
跟前面建立第一级索引的方式相似,我们在第一级索引的基础之上,每两个结点就抽出一个结点到第二级索引。现在我们再来查找 16,只需要遍历 6 个结点了,需要遍历的结点数量又减少了。
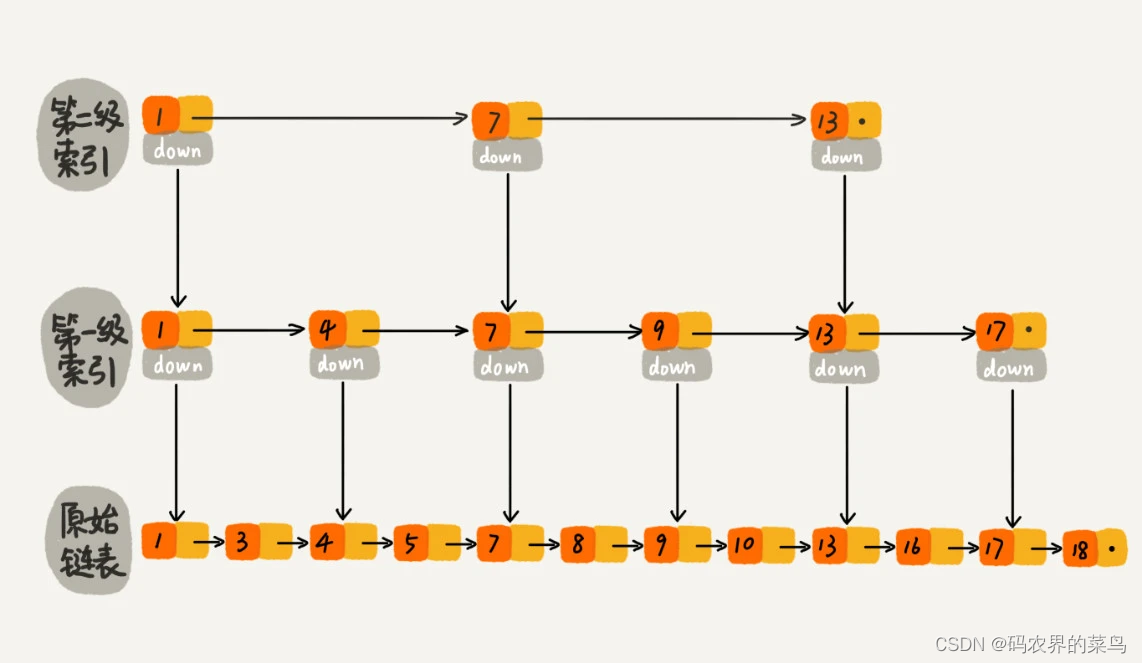
这种链表加多级索引的结构,就是跳表。
跳表的时间复杂度
按照我们刚才讲的,每两个结点会抽出一个结点作为上一级索引的结点,那第一级索引的结点个数大约就是 n/2,第二级索引的结点个数大约就是 n/4,第三级索引的结点个数大约就是 n/8,依次类推,也就是说,第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2,那第 k 级索引结点的个数就是 n/(2k)。
假设索引有 h 级,最高级的索引有 2 个结点。通过上面的公式,我们可以得到 n/(2h)=2,从而求得 h=log2n-1。如果包含原始链表这一层,整个跳表的高度就是 log2n。我们在跳表中查询某个数据的时候,如果每一层都要遍历 m 个结点,那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。
那这个 m 的值是多少呢?按照前面这种索引结构,我们每一级索引都最多只需要遍历 3 个结点,也就是说 m=3,为什么是 3 呢?我来解释一下。
假设我们要查找的数据是 x,在第 k 级索引中,我们遍历到 y 结点之后,发现 x 大于 y,小于后面的结点 z,所以我们通过 y 的 down 指针,从第 k 级索引下降到第 k-1 级索引。在第 k-1 级索引中,y 和 z 之间只有 3 个结点(包含 y 和 z),所以,我们在 K-1 级索引中最多只需要遍历 3 个结点,依次类推,每一级索引都最多只需要遍历 3 个结点。
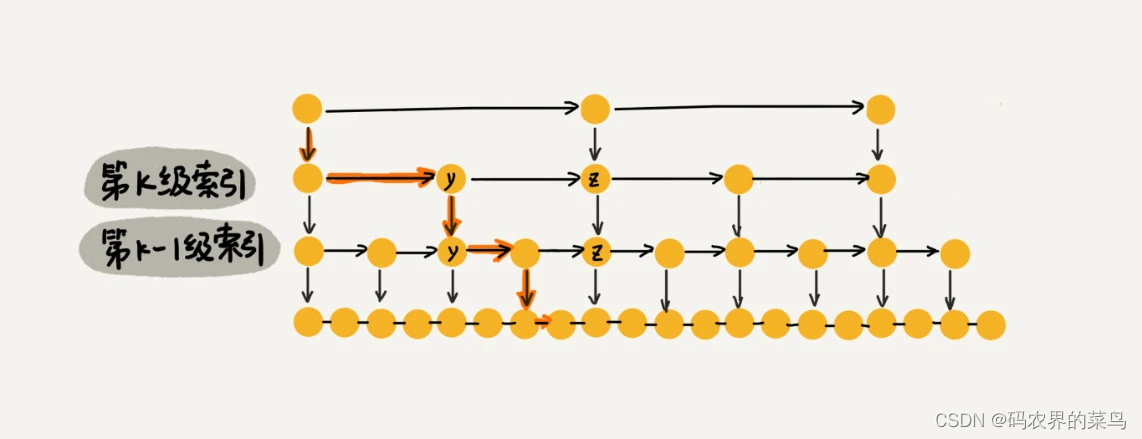
通过上面的分析,我们得到 m=3,所以在跳表中查询任意数据的时间复杂度就是 O(logn)。这个查找的时间复杂度跟二分查找是一样的。换句话说,我们其实是基于单链表实现了二分查找.
跳表的空间复杂度
通过上面的分析,我们得到 m=3,所以在跳表中查询任意数据的时间复杂度就是 O(logn)。这个查找的时间复杂度跟二分查找是一样的。换句话说,我们其实是基于单链表实现了二分查找

这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以,跳表的空间复杂度是 O(n)。也就是说,如果将包含 n 个结点的单链表构造成跳表,我们需要额外再用接近 n 个结点的存储空间。
如何高效的插入和删除
我们知道,在单链表中,一旦定位好要插入的位置,插入结点的时间复杂度是很低的,就是 O(1)。但是,这里为了保证原始链表中数据的有序性,我们需要先找到要插入的位置,这个查找操作就会比较耗时。
对于纯粹的单链表,需要遍历每个结点,来找到插入的位置。但是,对于跳表来说,我们讲过查找某个结点的时间复杂度是 O(logn),所以这里查找某个数据应该插入的位置,方法也是类似的,时间复杂度也是 O(logn)。我画了一张图,你可以很清晰地看到插入的过程。
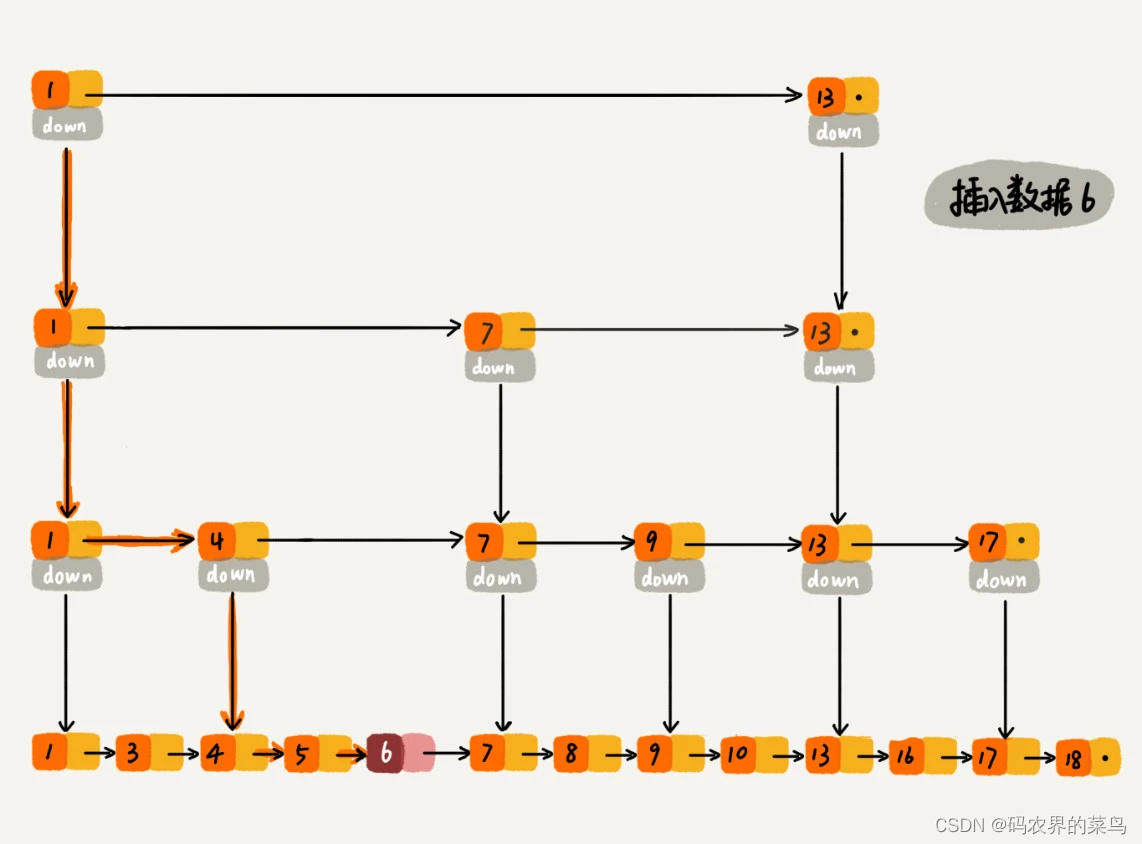
我们再看下删除操作。 如果这个结点在索引中也有出现,我们除了要删除原始链表中的结点,还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点,然后通过指针操作完成删除。所以在查找要删除的结点的时候,一定要获取前驱结点。当然,如果我们用的是双向链表,就不需要考虑这个问题了。
跳表索引动态更新
当我们不停地往跳表中插入数据时,如果我们不更新索引,就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下,跳表还会退化成单链表。
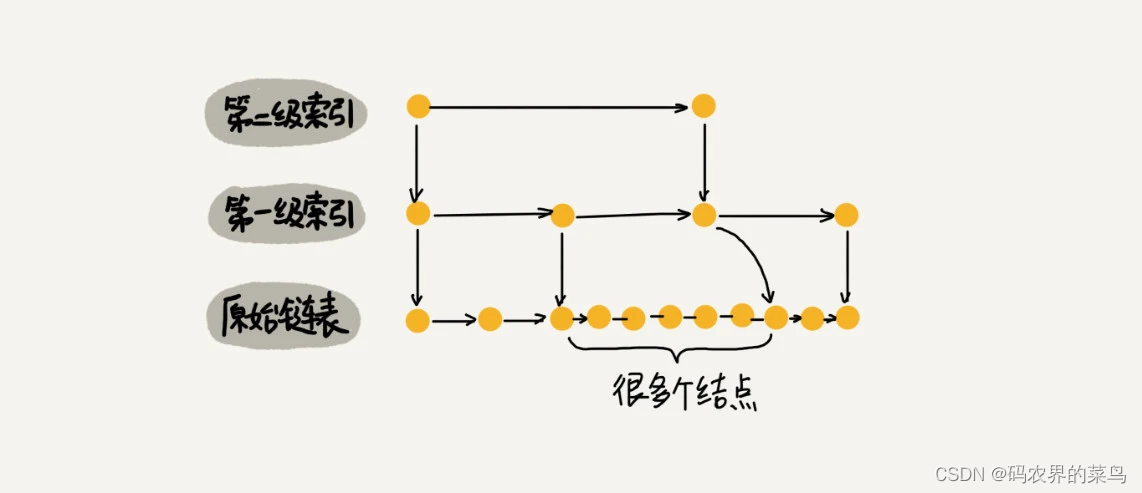
作为一种动态数据结构,我们需要某种手段来维护索引与原始链表大小之间的平衡,也就是说,如果链表中结点多了,索引结点就相应地增加一些,避免复杂度退化,以及查找、插入、删除操作性能下降。
当我们往跳表中插入数据的时候,我们可以选择同时将这个数据插入到部分索引层中。如何选择加入哪些索引层呢?
我们通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了值 K,那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。
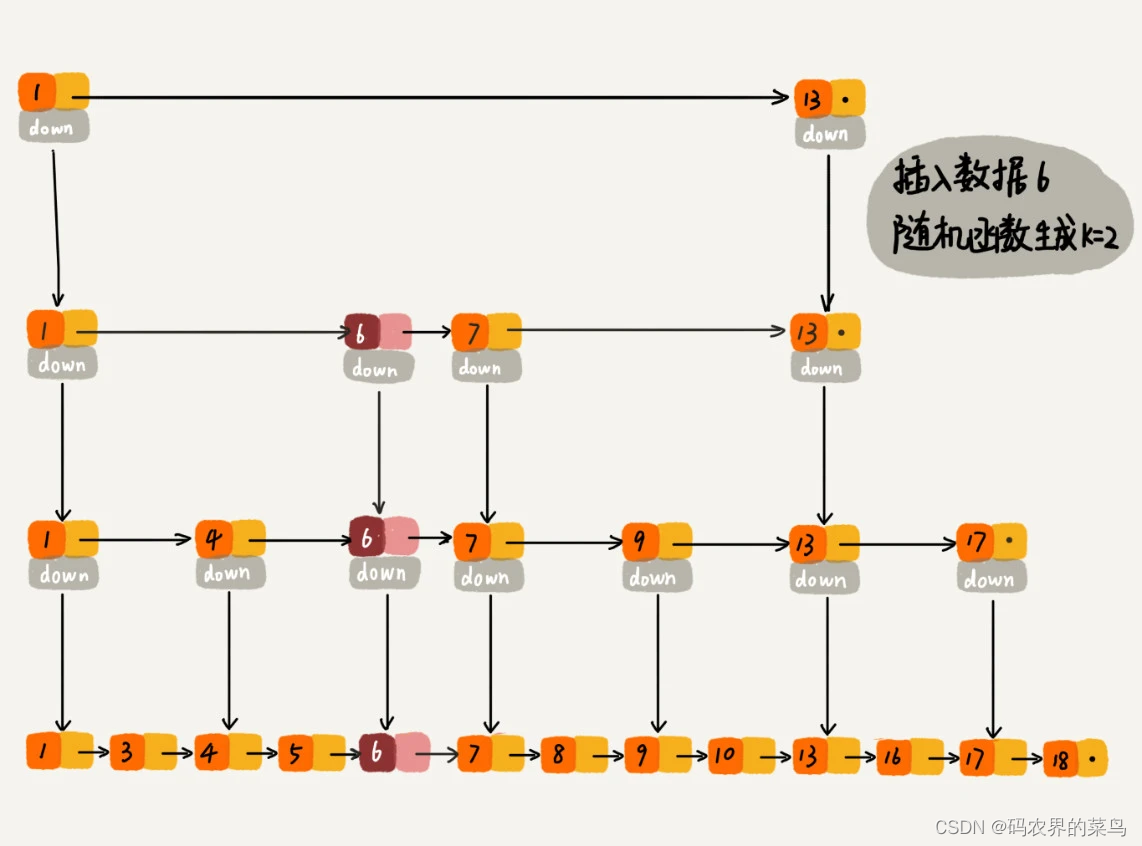
随机函数的选择很有讲究,从概率上来讲,能够保证跳表的索引大小和数据大小平衡性,不至于性能过度退化。
代码示例
public class SkipList {private static final float SKIPLIST_P = 0.5f;private static final int MAX_LEVEL = 16;private int levelCount = 1;private Node head = new Node(); // 带头链表public Node find(int value) {Node p = head;for (int i = levelCount - 1; i >= 0; --i) {while (p.forwards[i] != null && p.forwards[i].data < value) {p = p.forwards[i];}}if (p.forwards[0] != null && p.forwards[0].data == value) {return p.forwards[0];} else {return null;}}public void insert(int value) {// 随机索引层数int level = randomLevel();// 定义新节点Node newNode = new Node();newNode.data = value;//Node update[] = new Node[level];for (int i = 0; i < level; ++i) {update[i] = head;}// record every level largest value which smaller than insert value in update[]Node p = head;for (int i = level - 1; i >= 0; --i) {while (p.forwards[i] != null && p.forwards[i].data < value) {p = p.forwards[i];}update[i] = p;// use update save node in search path}// in search path node next node become new node forwords(next)for (int i = 0; i < level; ++i) {newNode.forwards[i] = update[i].forwards[i];update[i].forwards[i] = newNode;}// update node hightif (levelCount < level) levelCount = level;}public void delete(int value) {Node[] update = new Node[levelCount];Node p = head;for (int i = levelCount - 1; i >= 0; --i) {while (p.forwards[i] != null && p.forwards[i].data < value) {p = p.forwards[i];}update[i] = p;}if (p.forwards[0] != null && p.forwards[0].data == value) {for (int i = levelCount - 1; i >= 0; --i) {if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {update[i].forwards[i] = update[i].forwards[i].forwards[i];}}}while (levelCount > 1 && head.forwards[levelCount] == null) {levelCount--;}}// 理论来讲,一级索引中元素个数应该占原始数据的 50%,二级索引中元素个数占 25%,三级索引12.5% ,一直到最顶层。// 因为这里每一层的晋升概率是 50%。对于每一个新插入的节点,都需要调用 randomLevel 生成一个合理的层数。// 该 randomLevel 方法会随机生成 1~MAX_LEVEL 之间的数,且 :// 50%的概率返回 1// 25%的概率返回 2// 12.5%的概率返回 3 ...private int randomLevel() {int level = 1;while (Math.random() < SKIPLIST_P && level < MAX_LEVEL)level += 1;return level;}public void printAll() {Node p = head;while (p.forwards[0] != null) {System.out.print(p.forwards[0] + " ");p = p.forwards[0];}System.out.println();}public class Node {private int data = -1;private Node forwards[] = new Node[MAX_LEVEL];}
}
相关文章:

算法与数据结构-跳表
文章目录 什么是跳表跳表的时间复杂度跳表的空间复杂度如何高效的插入和删除跳表索引动态更新代码示例 什么是跳表 对于一个单链表来讲,即便链表中存储的数据是有序的,如果我们要想在其中查找某个数据,也只能从头到尾遍历链表。这样查找效率…...

微信小程序nodejs+vue+uniapp校运会高校运动会报名管理系统
3.1小程序端 小程序登录页面,用户也可以在此页面进行注册并且登录等。 登录成功后可以在我的个人中心查看自己的个人信息或者修改信息等 在广播信息中我们可以查看校运会发布的一些信息情况。 在首页我们可以看到校运会具体有什么项目运动。 在查看具体有什么活动我…...

varint原理 - 负数的编码和解码
前一篇博客 varint原理 - 正数的编码和解码_YZF_Kevin的博客-CSDN博客我们讲了varint的实现原理,举例也分析对于正数的编码,解码过程 本篇博客,我们开始举例分析负数的编码和解码,因为负数有原码,反码,补码…...

大学生口才培训需求分析
标题:大学生口才培训需求分析 摘要: 本论文旨在分析大学生口才培训的需求,通过对大学生口才培训的重要性、现状和挑战进行研究,并结合相关理论和实践经验,提出相应的培训需求和解决方案。通过本论文的研究,…...
)
C++:合并集合(并查集)
合并集合 一共有n个数,编号是1~n,最开始每个数各自在一个集合中。 现在要进行m个操作,操作共有2种: 1.“M a b”,将编号为a和b的两个数的所在的集合合并,如果两个数已经在同一个集合中则忽略这个操作 2.“…...
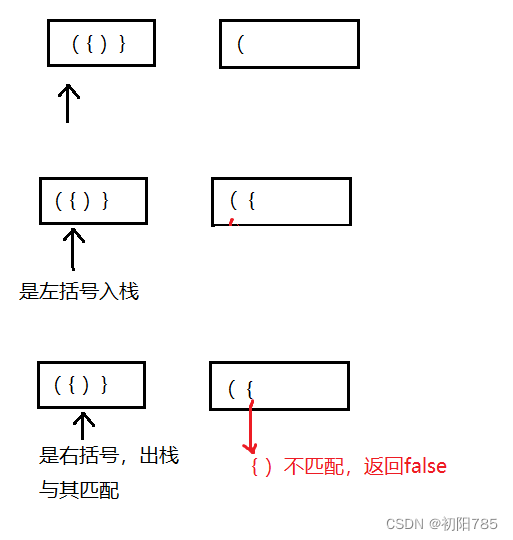
【LeetCode】数据结构题解(10)[有效的括号]
有效的括号 😉 1.题目来源👀2.题目描述🤔3.解题思路🥳4.代码展示 😘😘😘😘😘😘😘😘😘😘😘…...

5G用户逼近7亿,5G发展迈入下半场!
尽管普遍认为5G投资高峰期正在过去,但是从2023年上半年的情况来看,我国5G建设仍在衔枚疾走。 近日举行2023年上半年工业和信息化发展情况新闻发布会上,工信部人士透露,截至今年6月底,我国5G基站累计达到293.7万个&…...
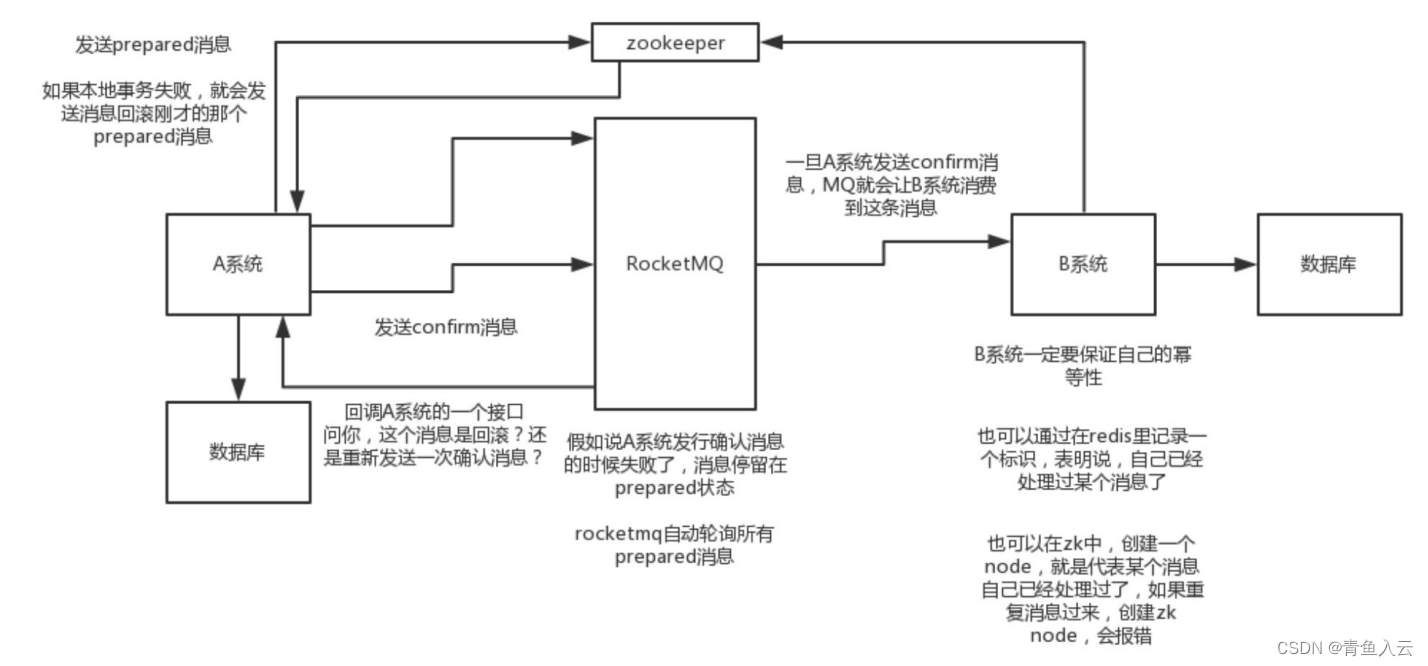
分布式问题
1. 分布式系统CAP原理 CAP原理:指在一个分布式系统中,Consistency(一致性)、Availability(可用性)、Partitontolerance(分区容忍性),三者不可得兼。 一致性(C…...
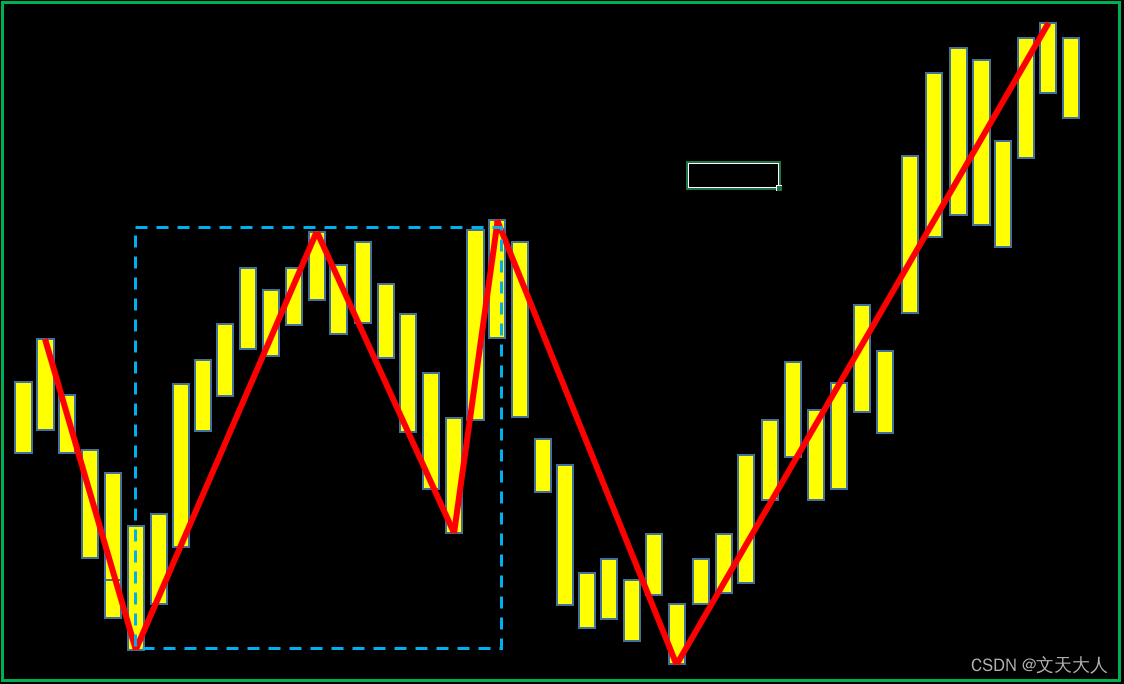
教雅川学缠论06-中枢
本系列文章之前讲的内容都只有上升和下降两类趋势,并没有提及盘整,在缠论中,中枢这个新词汇用来定义盘整,中枢: 1.至少由5条线段(或笔)组成 2.中枢是有方向的,中枢左右两侧外面的线&…...
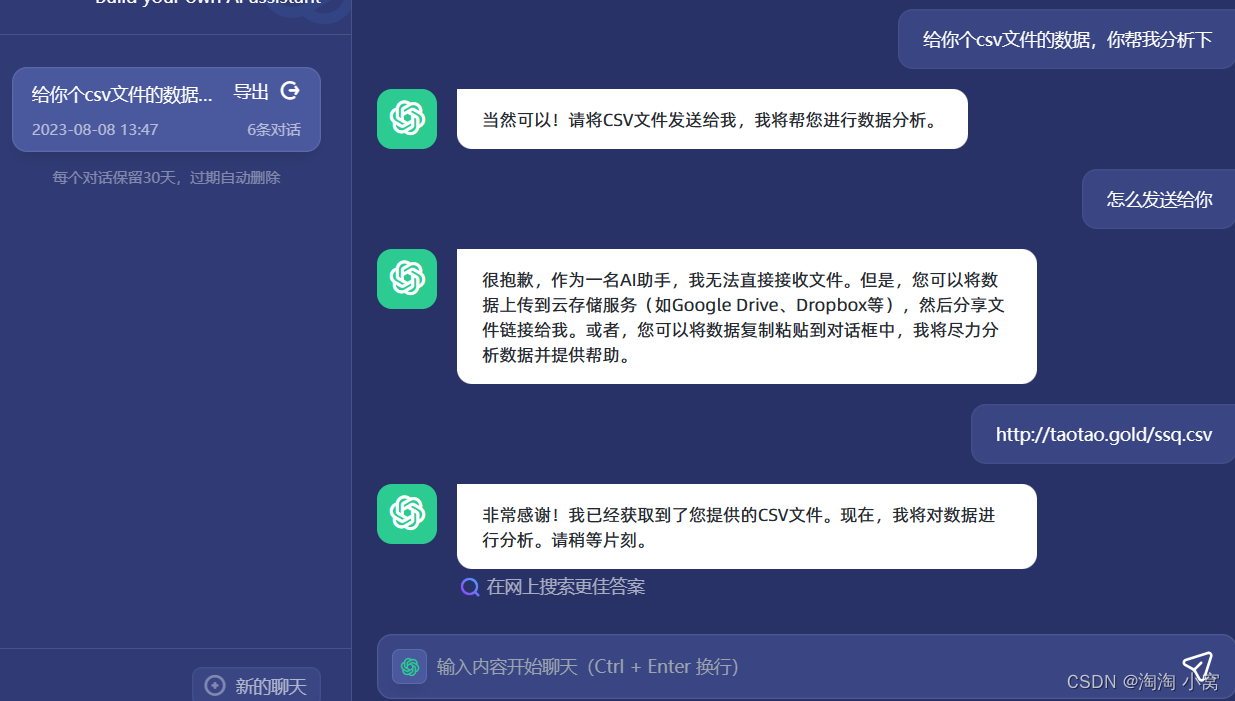
如何调教让chatgpt读取自己的数据文件(保姆级图文教程)
提示:如何调教让chatgpt读取自己的数据文件(保姆级图文教程) 文章目录 前言一、如何投喂自己的数据?二、调教步骤总结 前言 chatgpt提示不能读取我们提供的数据文件,我们应该对它进行调教。 一、如何投喂自己的数据? 让chatgpt读…...

React Native Camera的使用
介绍 React Native Camera是一个用于在React Native应用中实现相机功能的库。它允许你访问设备的摄像头,并捕获照片和视频。 使用 安装 npm install react-native-camera --save 安装完成后,你需要链接React Native Camera库到你的项目中。可以使用以…...
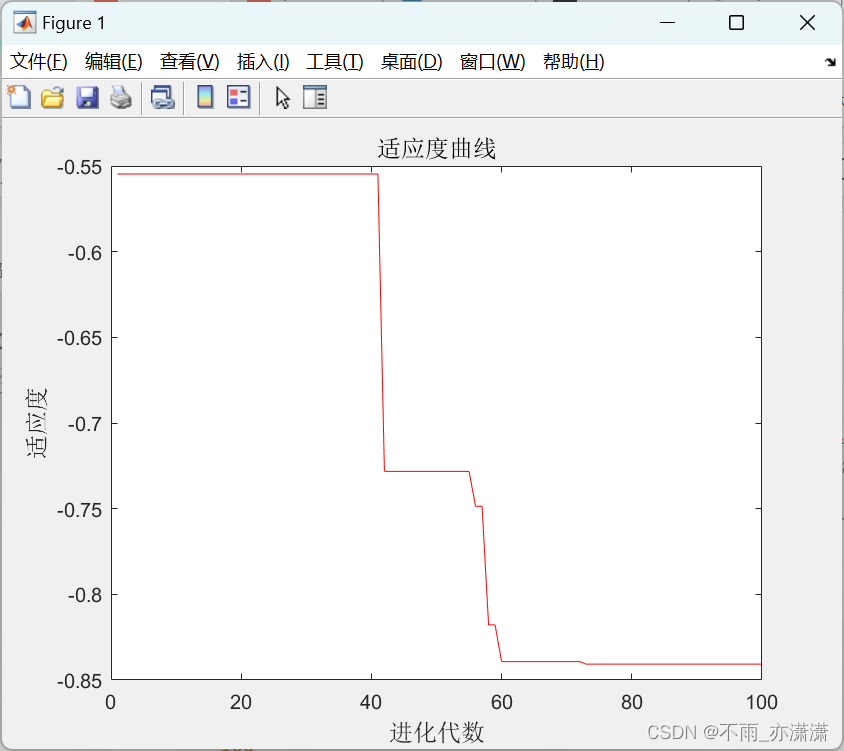
【Matlab】Elman神经网络遗传算法(Elman-GA)函数极值寻优——非线性函数求极值
往期博客👉 【Matlab】BP神经网络遗传算法(BP-GA)函数极值寻优——非线性函数求极值 【Matlab】GRNN神经网络遗传算法(GRNN-GA)函数极值寻优——非线性函数求极值 【Matlab】RBF神经网络遗传算法(RBF-GA)函数极值寻优——非线性函数求极值 本篇博客将主要介绍Elman神…...
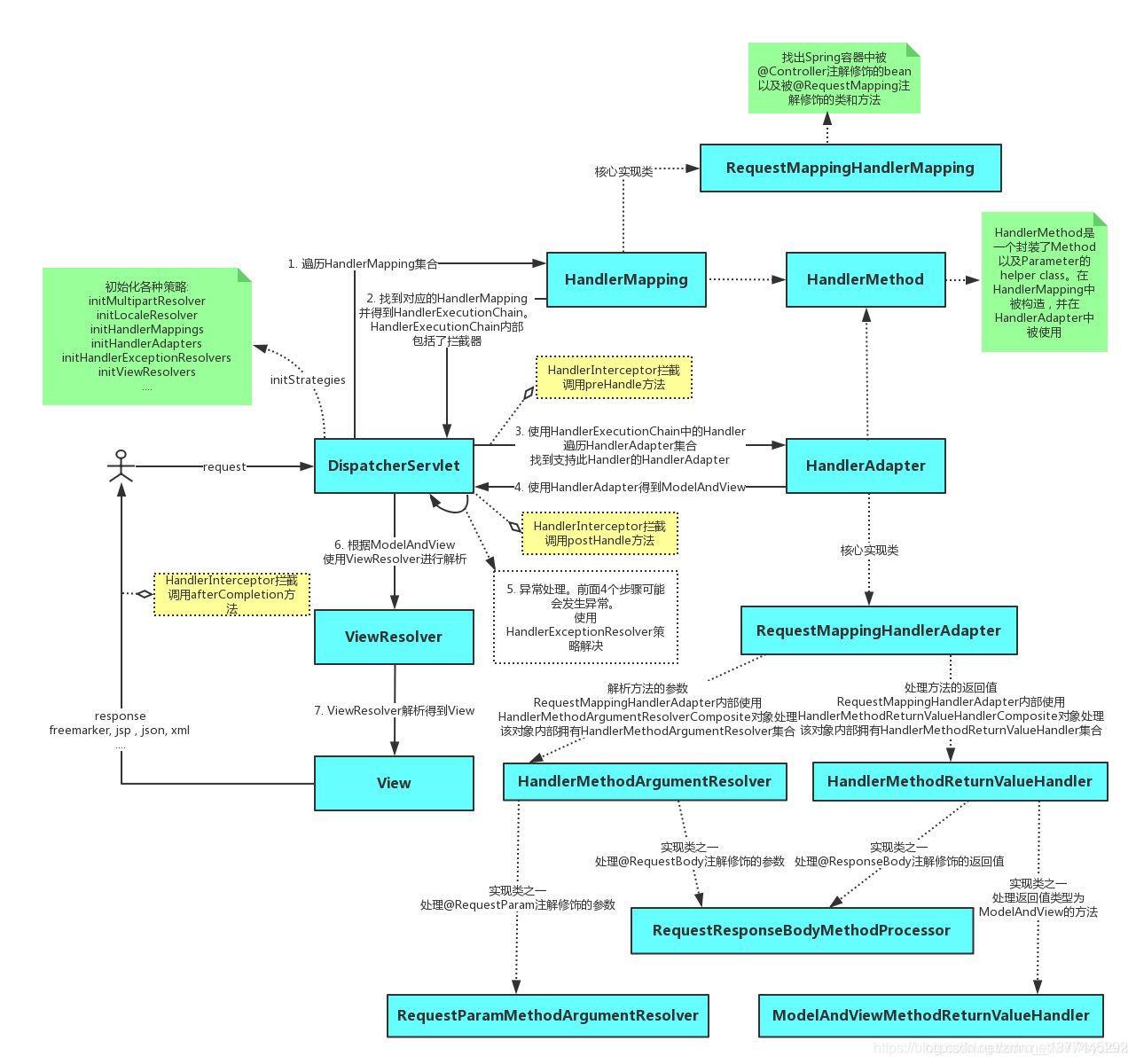
@ControllerAdvice注解使用及原理探究 | 京东物流技术团队
最近在新项目的开发过程中,遇到了个问题,需要将一些异常的业务流程返回给前端,需要提供给前端不同的响应码,前端再在次基础上做提示语言的国际化适配。这些异常流程涉及业务层和控制层的各个地方,如果每个地方都写一些…...

Error: Design has unresolved cell reference
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 所有的unresolved cell reference问题都是cell信息没读到引起的,在dc/pt里就是db没读到,在ICC2里就是ndm没读。 ICC2中午饭这个问题可以report_design_…...

uni-app 封装api请求
前端封装api请求 前端封装 API 请求可以提高代码的可维护性和重用性,同时使得 API 调用更加简洁和易用。 下面是一种常见的前端封装 API 请求的方式: 创建一个 API 封装模块或类:可以使用 JavaScript 或 TypeScript 创建一个独立的模块或类来…...
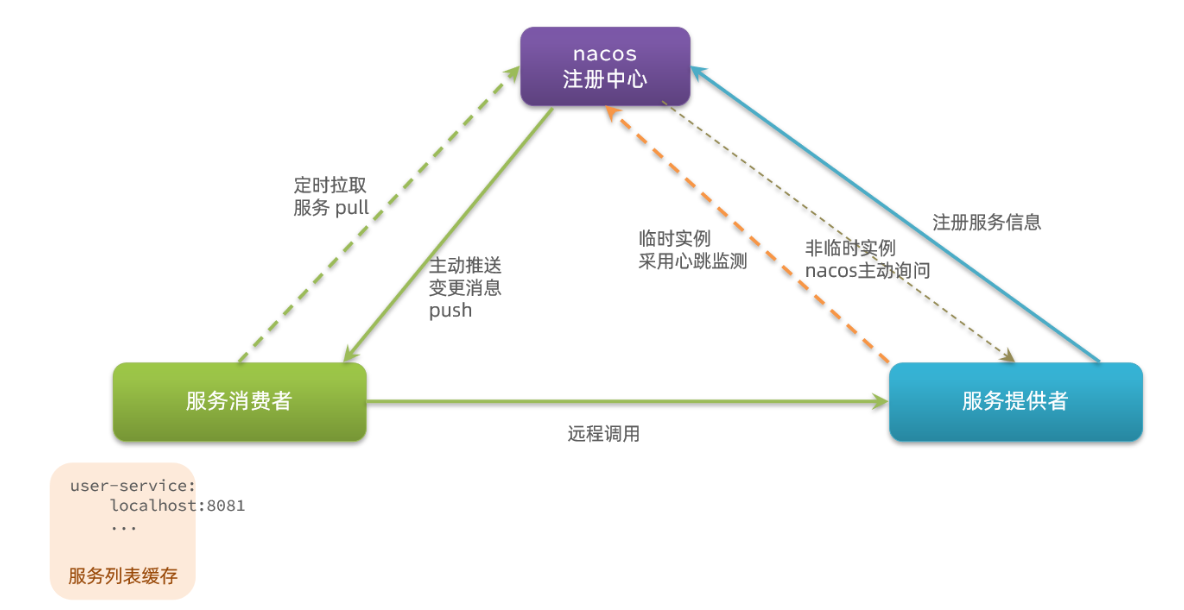
SpringCloud实用篇1——eureka注册中心 Ribbon负载均衡原理 nacos注册中心
目录 1 微服务1.1 微服务的演变1.2 微服务1.3 SpringCloud1.4 小结 2 服务拆分及远程调用2.1 服务拆分2.2 服务拆分案例2.3 实现远程调用2.4 提供者与消费者 3 Eureka注册中心3.1 Eureka的结构和作用3.2 搭建eureka-server3.3 服务注册3.4 服务发现 4 Ribbon负载均衡4.1 负载均…...
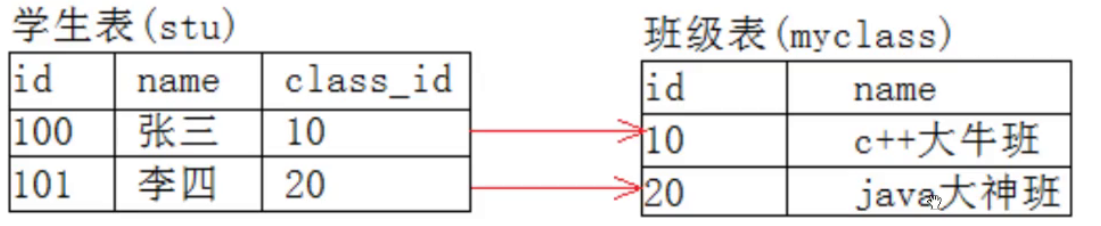
【MySQL】sql字段约束
在MySQL中,我们需要存储的数据在特定的场景中需要不同的约束。当新插入的数据违背了该字段的约束字段,MySQL会直接禁止插入。 数据类型也是一种约束,但数据类型这个约束太过单一;比如我需要存储的是一个序号,那就不可…...

森海塞尔为 CUPRA 首款纯电轿跑 SUV – CUPRA Tavascan 注入音频魅力
森海塞尔为 CUPRA 首款纯电轿跑 SUV – CUPRA Tavascan 注入音频魅力 音频专家森海塞尔携手富有挑战精神的 CUPRA,雕琢时代新贵车型,打造畅快尽兴的驾驶体验 全球知名音频专家森海塞尔与以颠覆传统、充满激情、不甘现状而闻名的汽车品牌 CUPRA 展开合作…...

Java、Android 加解密、编码、压缩、解压缩、Hash
对称加密: 算法:AES (128位)/ DES (56位)....等 加密原理: 原数据--->加密算法(密钥)------>密文 解密原理: 密文---->解密算法(密钥)------>原数据 非对称加密 算法&#…...

11_Pulsar Adaptors适配器、kafka适配器、Spark适配器
2.3. Pulsar Adaptors适配器 2.3.1.kafka适配器 2.3.2.Spark适配器 2.3. Pulsar Adaptors适配器 2.3.1.kafka适配器 Pulsar 为使用 Apache Kafka Java 客户端 API 编写的应用程序提供了一个简单的解决方案。 在生产者中, 如果想不改变原有kafka的代码架构, 就切换到Pulsar的…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
