ACM数论 裴蜀定理(贝祖定理)
一.内容定义
「裴蜀定理」,又称贝祖定理(Bézout's lemma)。是一个关于最大公约数的定理。其内容定义为:对于不全为零的任意整数 a 和 b,记二者的最大公约数为 g 即 gcd(a,b) = g,则对于任意整数 x 和 y 都一定满足 ax+by 是 g 的倍数。特别地,一定存在整数 x 和 y 的解,使得 ax+by=gcd(a,b) 成立。它的一个重要推论为:a,b互质的充分必要条件是存在整数x,y 使 ax+by=1; 或者说对于方程 ax+by=1 只有整数a和b互质时,方程才有整数解x,y。
「裴蜀定理」也可以推广到多个整数的情况。对于不全为零的任意 n 个整数 ,记这 n 个数的最大公约数为
,则对于任意 n 个整数
都满足
是 g 的倍数。特别的,一定存在一个整数序列的解
使得
成立。 它的一个重要的推论为:正整数
到
的最大公约数是 1 的充分必要条件是存在 n 个整数
到
满足
二.证明与应用
1.证明
裴蜀定理的证明在本文就不再赘述,该定理是一个很简单但是又非常重要的基本定理。这里给出两个比较官方的证明,请参考如下:
- 「裴蜀定理」百度百科
- 「裴蜀定理」OI Wiki
2.应用
裴蜀定理作为一个非常重要的基本定理,一方面可以在一些算法题目中作为关键的解题思路出现;另一方面,该定理也是一些算法和证明的推导基础,比如 扩展欧几里得算法、线性同余方程等。可以参考我之前的文章会更加清晰:
- 「扩展欧几里得算法」CSDN BLOG
三.例题
1.「检查好数组」LeetCode 1250
给你一个正整数数组 nums,你需要从中任选一些子集,然后将子集中每一个数乘以一个 任意整数,并求出他们的和。假如该和结果为 1,那么原数组就是一个「好数组」,则返回 True;否则请返回 False。
原题要求可以转换为求在数组中是否存在 ,根据裴蜀定理可知,该问题即为求解数组中是否存在任意一组互质的数。
正面去思考的话问题比较复杂,我们需要考虑是否存在两两互质、三个互质 ...,时间复杂度较高。但是从反面去思考的话问题就简单很多:一个数组要么是「好数组」,要么就是「非好数组」;如果整个数组是「非好数组」,就意味着数组中不存在任意一组互质的数(任意两两都不互质),那么我们直接求整个数组 的最大公约数即可。若全部数字的最大公约数等于 1 则原数组为「好数组」,否则不是。
#include <iostream>
#include <bits/stdc++.h>
using namespace std;class Solution {
public:int gcd(int a,int b){return b==0?a:gcd(b,a%b);}bool isGoodArray(vector<int>& nums) {int len = nums.size();int x = nums[0];for(int i = 1;i<len;i++){if(x==1)break;x = gcd(x,nums[i]);}return x == 1;}
};
相关文章:
ACM数论 裴蜀定理(贝祖定理)
一.内容定义 「裴蜀定理」,又称贝祖定理(Bzouts lemma)。是一个关于最大公约数的定理。其内容定义为:对于不全为零的任意整数 a 和 b,记二者的最大公约数为 g 即 gcd(a,b) g,则对于任意整数 x 和 y 都一定…...
解析)
基础篇—CSS Position(定位)解析
CSS Position(定位) position 属性指定了元素的定位类型。 position 属性的五个值: relativefixedabsolutesticky元素可以使用的顶部,底部,左侧和右侧属性定位。然而,这些属性无法工作,除非是先设定position属性。他们也有不同的工作方式,这取决于定位方法。 1、static…...

正则表达式与grep
基本正则表达式BRE集合 匹配字符匹配次数位置锚定 符号作用^尖角号,用于模式的最正常,如“^haha”,匹配以haha单词开头的行$美元符,用于模式的最右侧,如“haha$”,表示haha单词结尾的行^$组合符ÿ…...
开发必备的IDEA 插件!效率提升 50 倍!
日常开发中,面向百度编程的程序员,很多时候,你跟大佬级别的差距,可能不仅仅是知识面的差距,还有就是开发效率的差距。以下是我常用的几个IDEA插件,废话不多说,直接肝干货! 1. Codot…...

aws eks 集群访问ecr仓库拉取镜像的认证逻辑
本文主要讨论三个问题 ecr帮助程序在docker上如何配置eks集群访问ecr仓库的逻辑kubelet授权ecr的源码分析 ecr帮助程序 在docker环境下,可以通过在$HOME/.docker/config.json中指定凭证管理程序 docker login aws同样提供了证书助手,避免手动执行ecr认…...
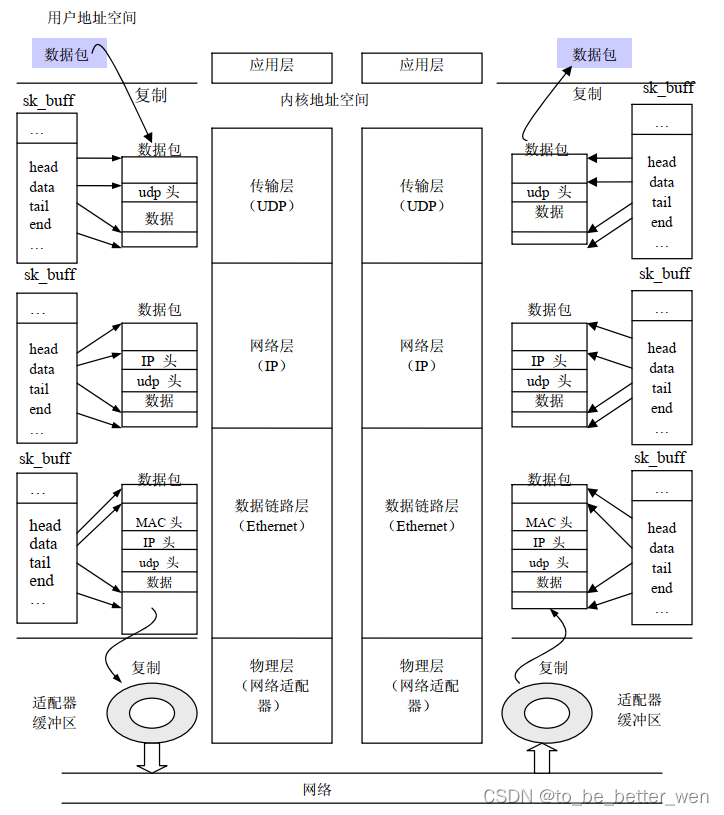
Linux Socket Buffer介绍
一. 前言 Linux内核网络子系统的实现之所以灵活高效,主要是在于管理网络数据包的缓冲器-socket buffer设计得高效合理。在Linux网络子系统中,socket buffer是一个关键的数据结构,它代表一个数据包在内核中处理的整个生命周期。 二. Socket Bu…...
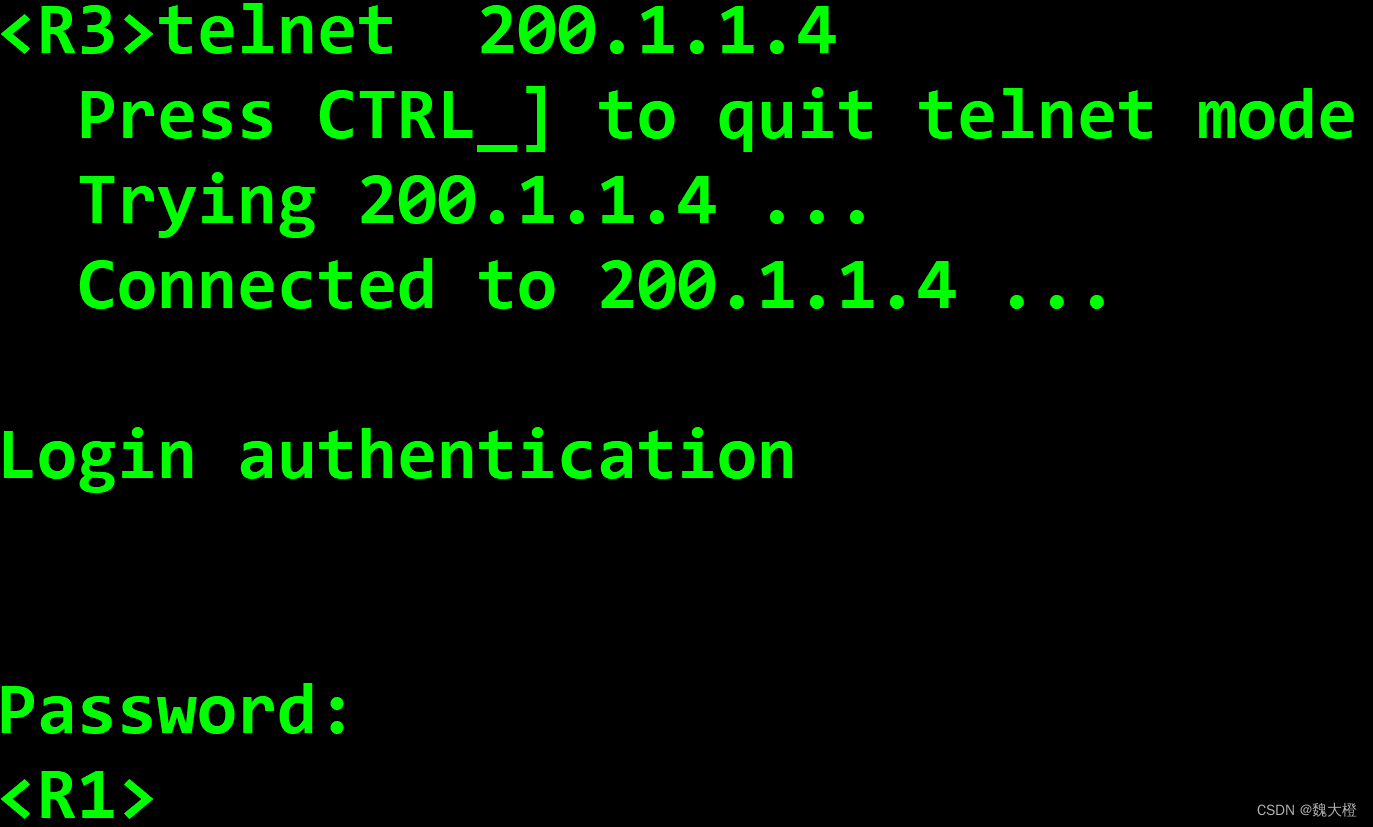
ACL与NAT
ACL---访问控制列表,是一种策略控制工具 功能:1.定义感兴趣流量(数据层面 ) 2.定义感兴趣路由(控制层面) ACL 条目表项组成: 编号规则:步数或者跳数默认值为5,…...

使用gdb来debug程序并查找Segmentation fault原因
GDB 调试前言GDB基础用法1.启动及退出调试2.设置参数3.执行程序4.流程控制5.设置断点6.输出信息7.查看栈帧8.info命令9.显示源码GDB调试coredump文件关注公众号【程序员DeRozan】,回复【1207】,免费获取计算机经典资料及现金红包 前言 在开发程序时&…...

vbs简单语法及简单案例
文章目录一、简单语法1、变量2、输入3、输出4、选择语句5、循环二、用记事本编译中文乱码问题三、制作一个简单vbs脚本表白一、简单语法 1、变量 语法: dim 变量名例: dim a,b a1 b2 msgbox ab运行: 2、输入 语法:InputBox(…...

学板绘课程学费一般多少钱
学板绘课程学费一般多少钱?培训机构的费用和师资、模式有关,价格贵不贵要结合相同类型的机构多多对比。因为好些平台做了很多的宣传广告,运营成本很高, 终羊毛出在羊身上,这样的机构知名度很高,但是性价比不…...
- 实现一个可以用的模板)
48.在ROS中实现local planner(1)- 实现一个可以用的模板
有了之前45.在ROS中实现global planner(1)- 实现一个可以用模板的global planner的经验, 现在再去创建一个local planner的包就容易多了 1. 创建包 创建 cd ~/pibot_ros/ros_ws/src # 这里可以使用自己的ros workspace catkin_create_pkg sample_loc…...
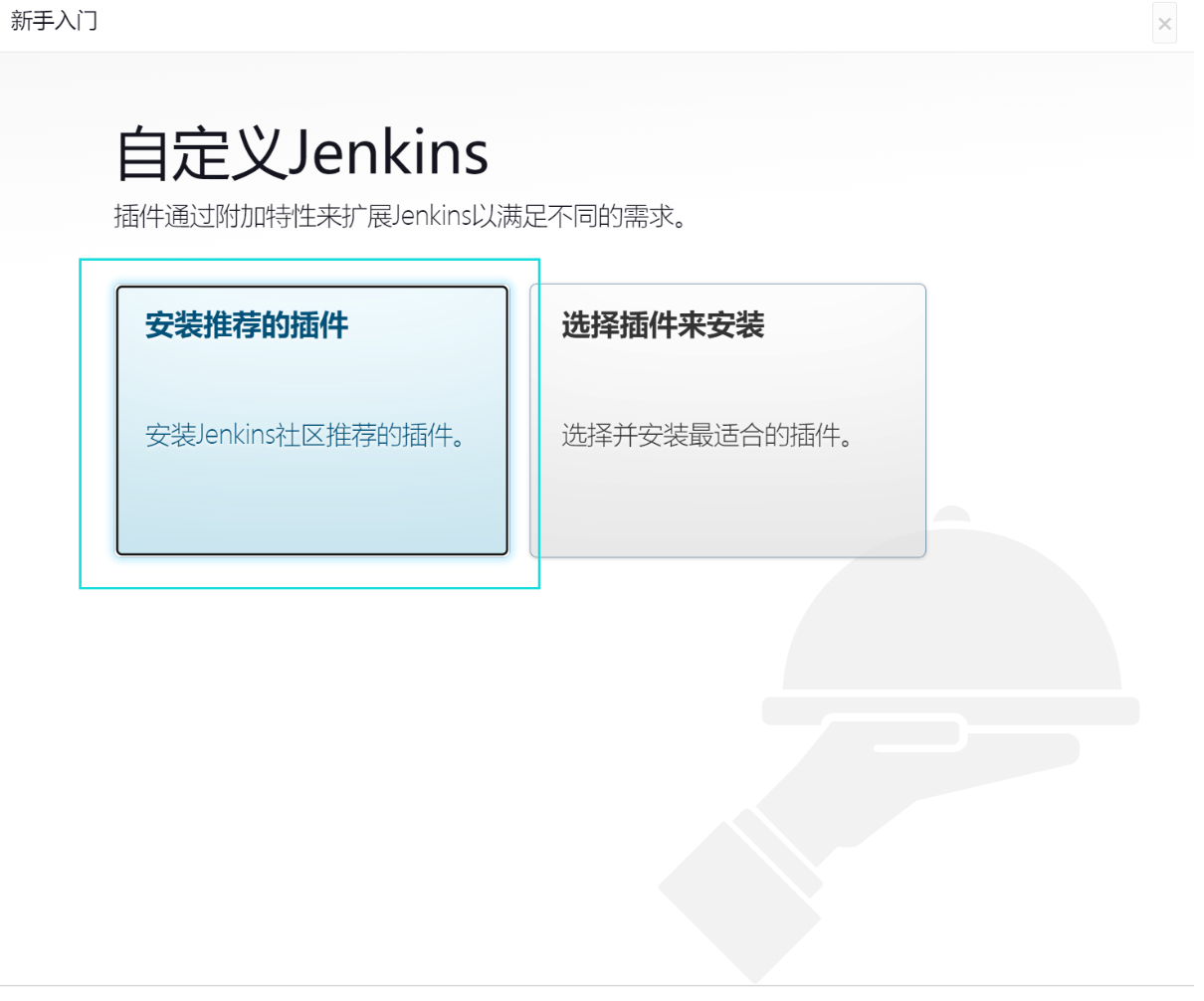
jenkins基础部署
一、jenkins是什么1.Jenkins的前身是Hudson,采用JAVA编写的持续集成开源工具。Hudson由Sun公司在2004年启动,第一个版本于2005年在java.net发布。2007年开始Hudson逐渐取代CruiseControl和其他的开源构建工具的江湖地位。在2008年的JavaOne大会上在开发者…...
Unity3D -知识点(1)
1.场景视图鼠标滚轮:场景放大缩小鼠标右键:场景左右平移场景编辑器中,能看到什么?网格,每一格大小为1unit,建模不同,规定不同,(对应屏幕上100个像素)世界坐标系y轴向上为正x轴向右为…...

【学习笔记】NOIP暴零赛3
博弈(game) 观察到博弈过程中胜负态不会发生改变,那么求出从每个棋子出发能走的最长链,然后背包即可。 复杂度O(nm)O(nm)O(nm)。 #include<bits/stdc.h> #define ll long long #define pb push_back using namespace std; const int mod9982443…...

Java JSR规范列表
Java JSR规范列表目录概述需求:设计思路实现思路分析1.JSR2.JSR方法3.web service4.Webservice:5.数据处理器拓展实现参考资料和推荐阅读Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,m…...

Java必备小知识点1
Java程序类型: Applications和AppletApplications:是指在计算机操作系统中运行的程序。是完整的程序,能独立运行。被编译后,用普通的Java解释器就可以使其边解释边执行。必定含有一个main方法,程序执行时,首先寻找main方法&#x…...

JavaScript作用域、闭包
文章目录作用域、作用域链作用域作用域链循环中的作用域自由变量、闭包自由变量闭包的定义、表现、应用如何确定在闭包中获取正确的变量总结作用域、作用域链 作用域 编程语言中存储、访问、修改变量当中的值是一项基本能力、存储变量、访问变量必须按照一定的规则࿰…...
 对象)
JavaScript Date(日期) 对象
JavaScript Date 对象是 JavaScript 中用于处理日期和时间的内置对象。它可以用于获取当前时间、设置日期和时间、计算日期和时间之间的差异、以及将日期和时间格式化为各种字符串格式。在本文中,我们将详细介绍 JavaScript Date 对象的作用和在实际工作中的用途。 …...

rust过程宏 proc-macro-workshop解题-4-sorted
名字版本号rust1.69.0OSubuntu 22.04这一大关卡介绍的是属性式过程宏。 第一关:01-parse-enum 还是简单的看我们是否已经实现了一个属性式过程宏的空架子,如果有这个空架子,就直接通过了。 use proc_macro::TokenStream; use proc_macro2; use syn;#[proc_macro_attribut…...
数据结构与算法—队列
队列 队列介绍 有序列表,可以用数组或者链表实现。遵循先进先出原则。 数组实现队列 public class ArrayQueue {public static void main(String[] args) {ArrayQueue queue new ArrayQueue(3);// 接收用户输入char key ;Scanner sc new Scanner(System.in);…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
