时间复杂度空间复杂度相关练习题
1.消失的数字
【题目】:题目链接
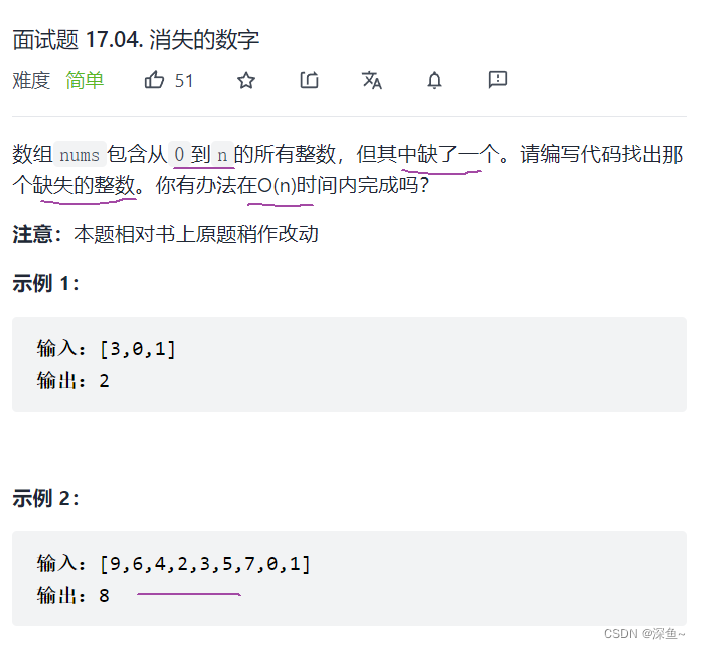
思路1:排序——》qsort快排——》时间复杂度O(n*log2n) 不符合要求
思路2:(0+1+2+3+...+n)-(a[0]+a[1]+[2]+...+a[n-2]) ——》
时间复杂度O(N)空间复杂度为O(1)
(0+1+2+3+...+n)直接用等差数列求和就可
思路3:数组中是几就在第几个位置写一下这个值 ——》时间空间复杂度都为O(N)
思路4:给一个值x=0,
x先跟[0,n]的所有值异或,
x再跟数组中的每个值异或,最后x就是缺的那个数字
(异或的特点相同的数异或为0,0跟一个数异或为这个数,且异或满足交换律)
时间复杂度O(N) 空间复杂度O(1)
eg:假设[0,9]缺一个8,先让x=0跟[0,9]不缺8的数一个一个异或(0跟一个数异或为这个数,这样初始化以后就不会被x所影响),异或完的结果还是[0,9],然后这些值和缺8的数组异或,结果发现这两个数组中相同的两个数异或为0就没了(可以直接交换律理解),最后只剩下0和8异或,异或结果就是8(也就是缺少的数字)
【图解】: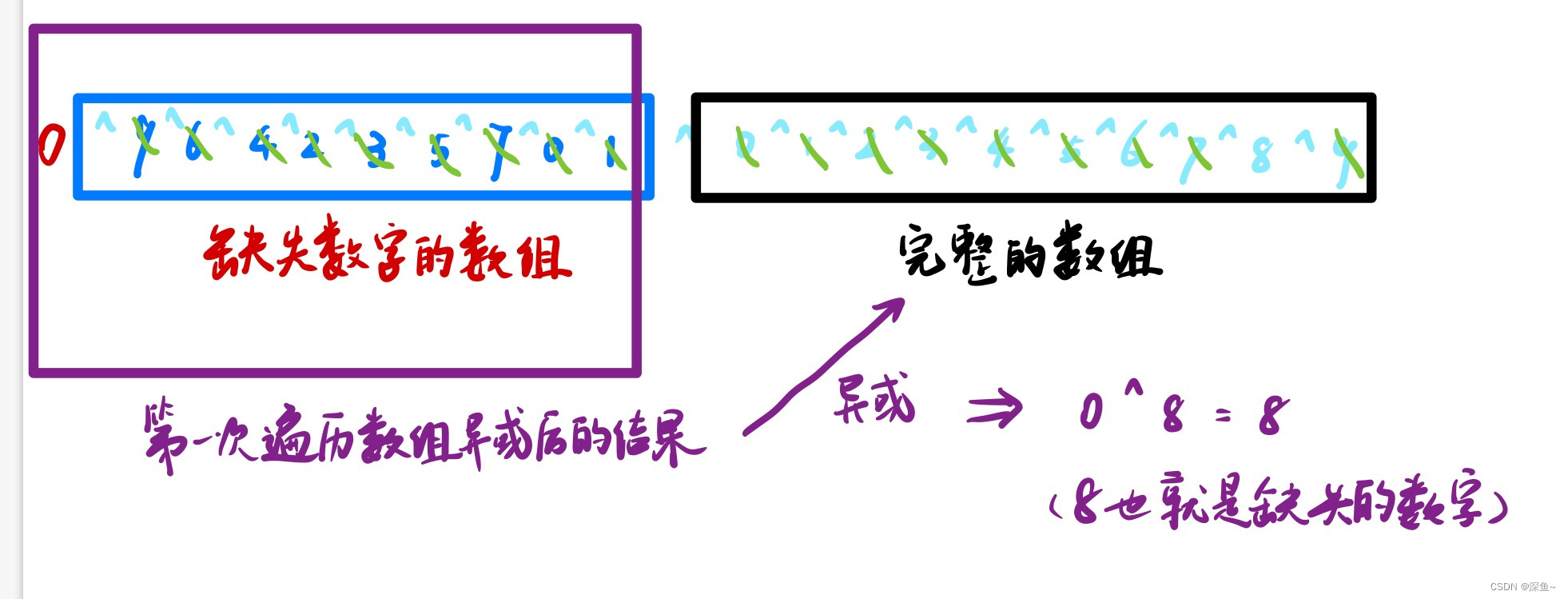
本题推荐思路2和思路4:时间空间复杂度最优
思路2代码实现:
int missingNumber(int* nums, int numsSize)
{//等差数列求和int sum=((1+numsSize)*numsSize)/2;//sum减去数组中的元素for(int i=0;i<numsSize;i++){sum-=nums[i];}return sum;
}思路4代码实现:
int missingNumber(int* nums, int numsSize){int x=0;//跟数组中的值异或for(int i=0;i<numsSize;i++)//这里少一个数,直接<{x^=nums[i];}//跟[0,9]的值异或for(int i=0;i<=numsSize;i++)//这里多一个数(n+1)个,<={x^=i;}return x;
}2.旋转数组
【题目】:题目链接


思路1:暴力求解,旋转K次(一次一次地移,直到旋转
时间复杂度:O(N*K)空间复杂度:O(1)
思路2:开辟额外空间,以空间换时间
(创建一个数组,要移动到前面的就放入数组,其他部分向后移动即可)
时间复杂度:O(N) 空间复杂度:O(N)
思路3:(1)前n-k个数字逆置
(2)后k个逆置
(3)整体逆置
时间复杂度:O(N) 空间复杂度:O(1)
这里肯定是思路3最优
代码演示:
void reverse(int *nums,int left,int right)
{while(left<right){int tmp=nums[left];nums[left]=nums[right];nums[right]=tmp;left++;right--;}
}
void rotate(int* nums, int numsSize, int k)
{k=k%numsSize;//倒置前n-k个数字reverse(nums,0,numsSize-k-1);//倒置后k个数字reverse(nums,numsSize-k,numsSize-1);//倒置整个数组reverse(nums,0,numsSize-1);
}k=k%numsSize;的意思就是如果k的大小大于numsSize的大小,那么就需要对k进行取模操作,这样避免重复操作,效率更高
本次数据结构时间空间复杂度练习的内容就到此啦,有什么问题欢迎评论区或者私信交流,觉得笔者写的还可以,或者自己有些许收获的,麻烦铁汁们动动小手,给俺来个一键三连,万分感谢 !

相关文章:

时间复杂度空间复杂度相关练习题
1.消失的数字 【题目】:题目链接 思路1:排序——》qsort快排——》时间复杂度O(n*log2n) 不符合要求 思路2:(0123...n)-(a[0]a[1][2]...a[n-2]) ——》 时间复杂度O(N)空间复杂度…...

Linux | Ubuntu18.04安装RTX 4060显卡驱动完整教程
文章目录 概述一、定义介绍二、操作教程(一)、前期准备1.进入终端界面2.关闭界面显示器3.禁用其他显卡驱动4.卸载残余显卡驱动5.下载驱动(二)、安装驱动1.给驱动程序赋予权限2.安装驱动3.检查结果(三)、后续问题1.黑屏问题概述 本节详细介绍了如何在ubuntu18系统安装4060显卡的…...
Mermaid语法使用
Mermaid语法使用 1. 基础类1.1 流程图1.2 时序图 2. 工程图2.1 类图2.2 Git图 1. 基础类 1.1 流程图 graph TBid1(圆角矩形)--普通线-->id2[矩形];subgraph 子图id2粗线>id3{菱形}id3-. 虚线.->id4>右向旗帜]id3--无箭头---id5((圆形))end方向定义 用词含义TB从…...
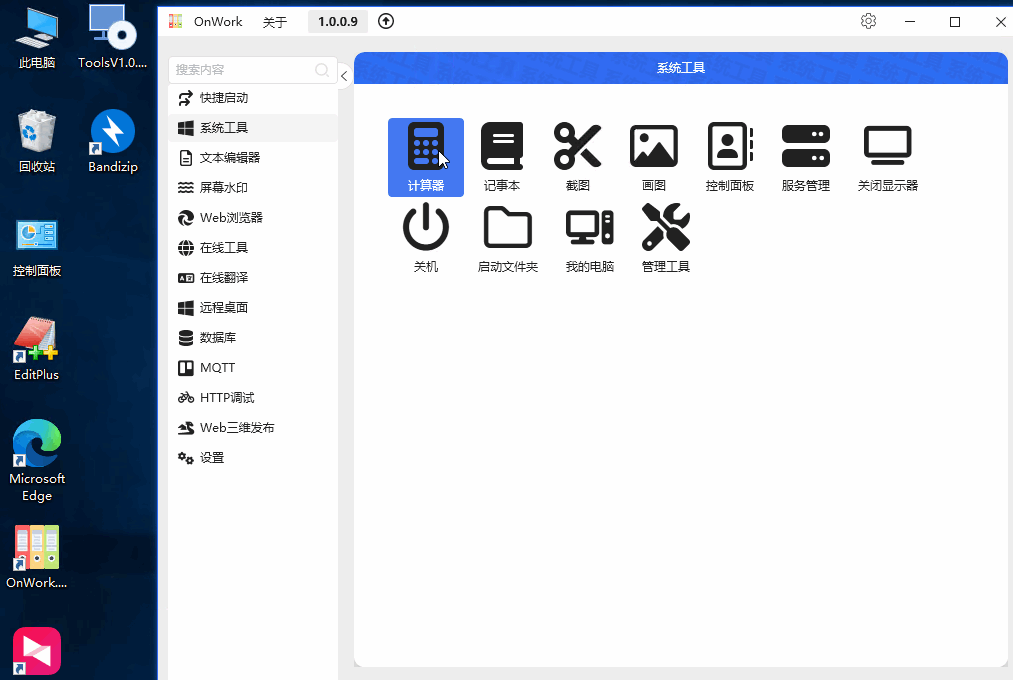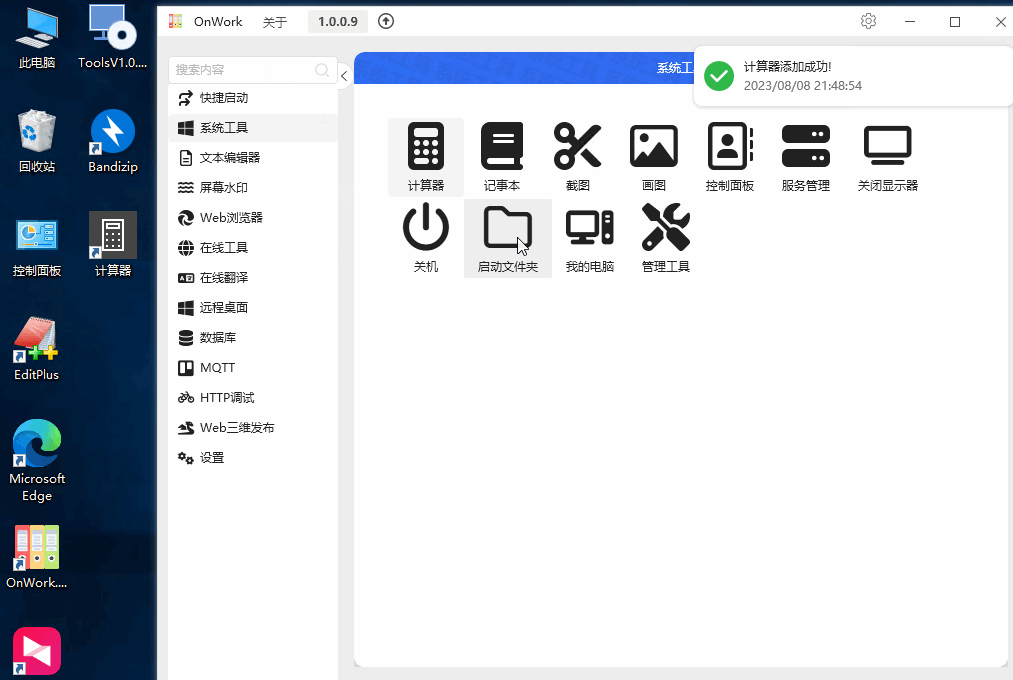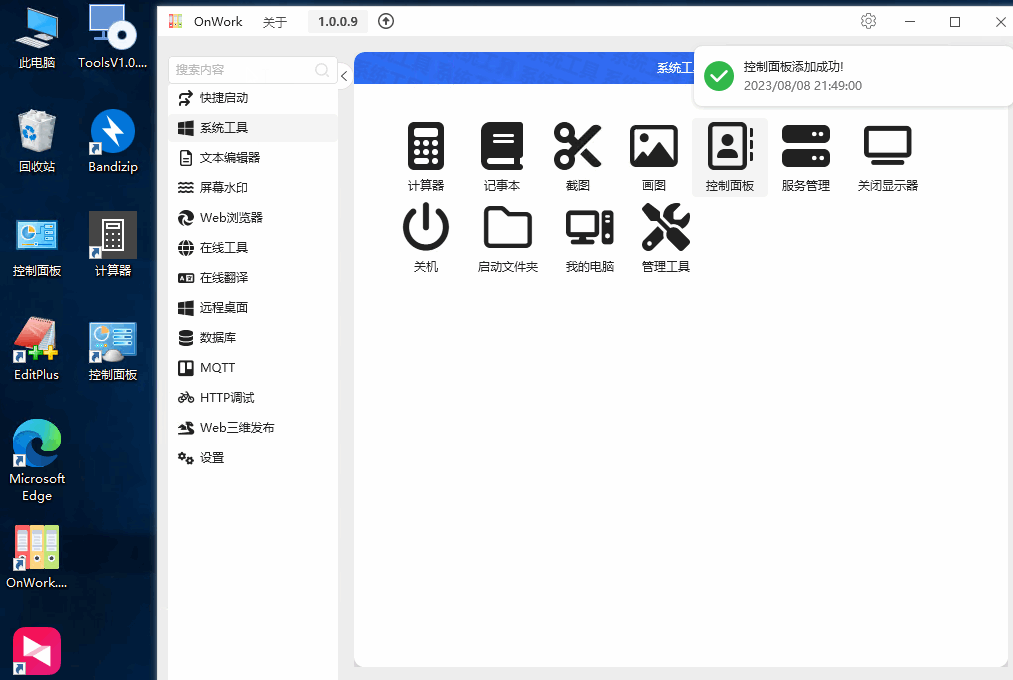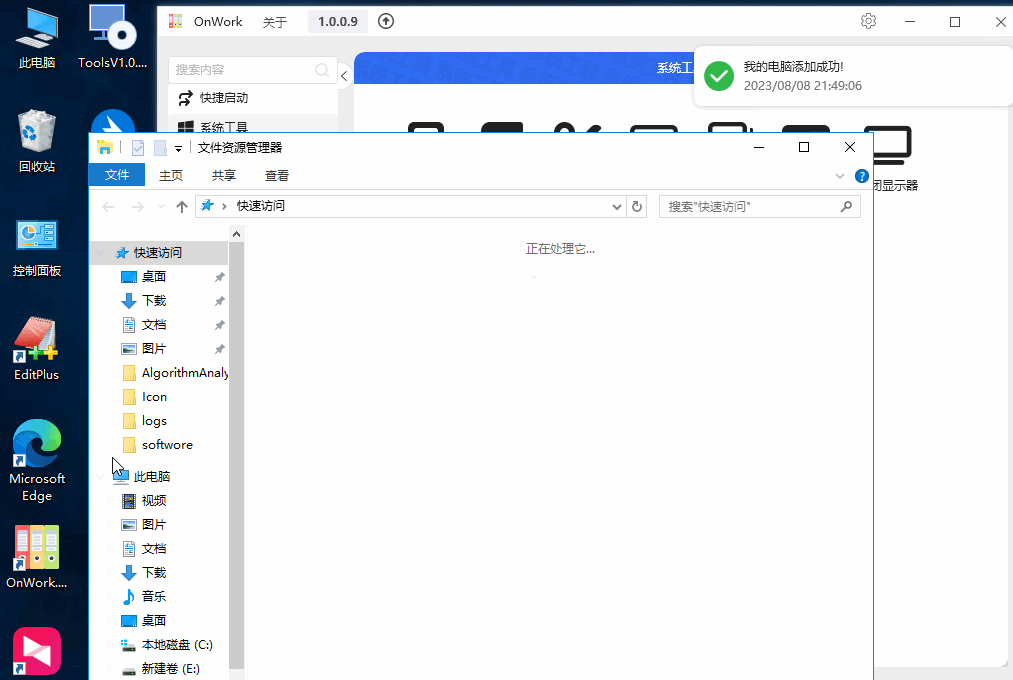
[OnWork.Tools]系列 05-系统工具
简介 系统工具主要是将Window常用工具的快捷启动的集合 双击快速启动 计算器,记事本,截图,画图工具 控制面板,服务管理,关闭显示器,关机 启动文件夹,我的电脑,管理工具 右键菜单 添加快捷方式到桌面...

SOME/IP学习笔记1
SOA概念 在SOA中,每个服务就好像我们每一个人在社会中扮演的角色,在对别人提供着服务的同时,同时也享受着别人提供出来的服务,人与人之间,既是彼此独立的,又是需要互相通讯的。服务提供者将功能具象为一组接口,这样使用者就能知道如何调用服务,完成某件事情,得到某个…...

Effective Java笔记(26)请不要使用原生态类型
首先介绍一些术语 。 声明中具有一个或者多个类型参数( type parameter )的类或者接口,就是泛型( generic )类或者接口 。 例如,List 接口就只有单个类型参数 E ,表示列表的元素类型 。这个接口…...

linux 内存 - KO内存占用
说明 KO(kernel module)占用的内存分为两部分: 静态占用 :ko insmod时系统固定分配的内存。动态申请 :代码中动态申请的内存,由于申请方式不同,统计的方式也可能不同,例如:使用vmalloc和kmall…...
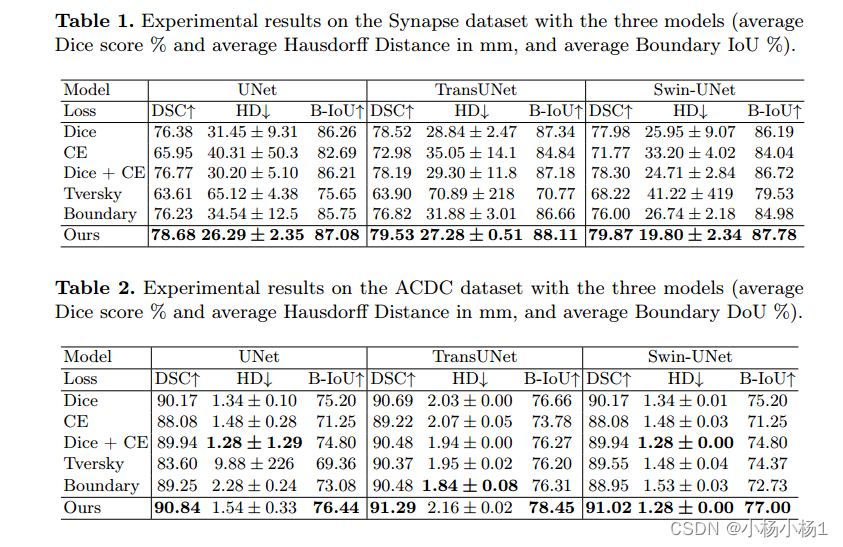
2023.8.7论文阅读
文章目录 CMUNeXt: An Efficient Medical Image Segmentation Network based on Large Kernel and Skip Fusion摘要本文方法实验结果 Boundary Difference Over Union Loss For Medical Image Segmentation(损失函数)摘要本文方法实验结果 CMUNeXt: An E…...
2023河南萌新联赛第(五)场:郑州轻工业大学 --Kruskal
题目描述 给定一张nnn个点的无向完全图,其中两点之间的路径边权为两点编号的按位与(编号为 (1,2,...,n)(1,2,...,n)(1,2,...,n)),即w(u,v)u&v(1≤u,v≤n)w\left(u, v \right )u\&v \left( 1 \le u, v \le n \right)w(u,v…...
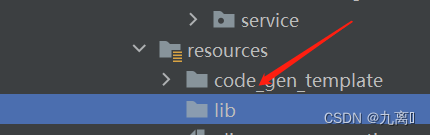
Maven引入本地jar包
maven做为一种强大的依赖管理工具,可以帮助我们更方便的管理项目中的依赖;而在使用过程中我们难免会有需要引入本地jar包的需求,这里踩过坑之后我分享俩种引入方式; 1.上传jar到本地maven仓库,再引入 使用此方法后可…...

Java并发编程实战——结构化并发应用程序
文章目录 6 任务执行6.1 在线程中执行任务6.1.1 串行地执行任务6.1.2 显式地为任务创建线程6.1.3 无限制创建线程的不足 6.2 Executor框架6.2.1 示例:基于Executor的Web服务器6.2.2 执行策略6.2.3 线程池6.2.4 Executor的生命周期6.2.5 延迟任务与周期任务 6.3 找出…...
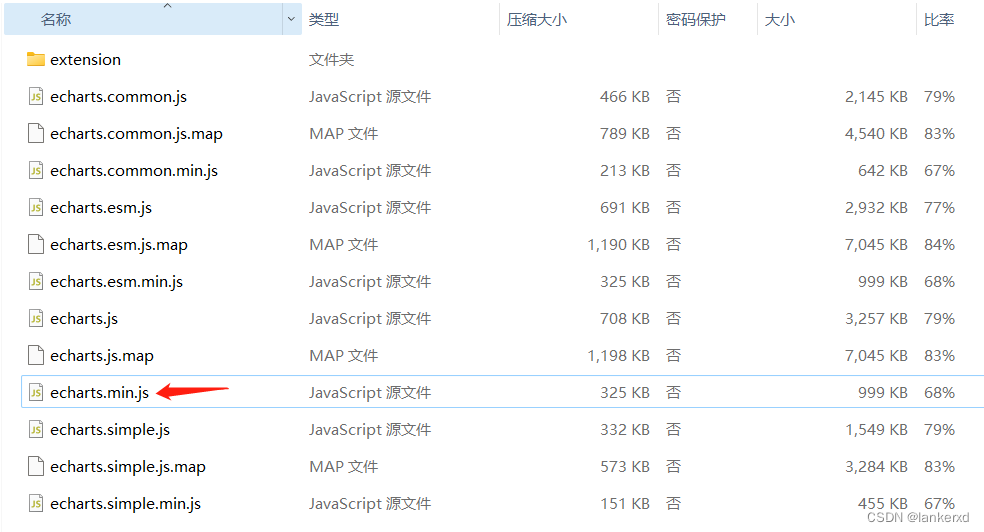
uniapp echarts 点击失效
这个问题网上搜了一堆,有的让你降版本,有的让你改源码。。。都不太符合预期,目前我的方法可以用最新的echarts。 这个方法就是由npm安装转为CDN,当然你可能会质疑用CDN这样会不稳定,那如果CDN的地址是本地呢࿱…...
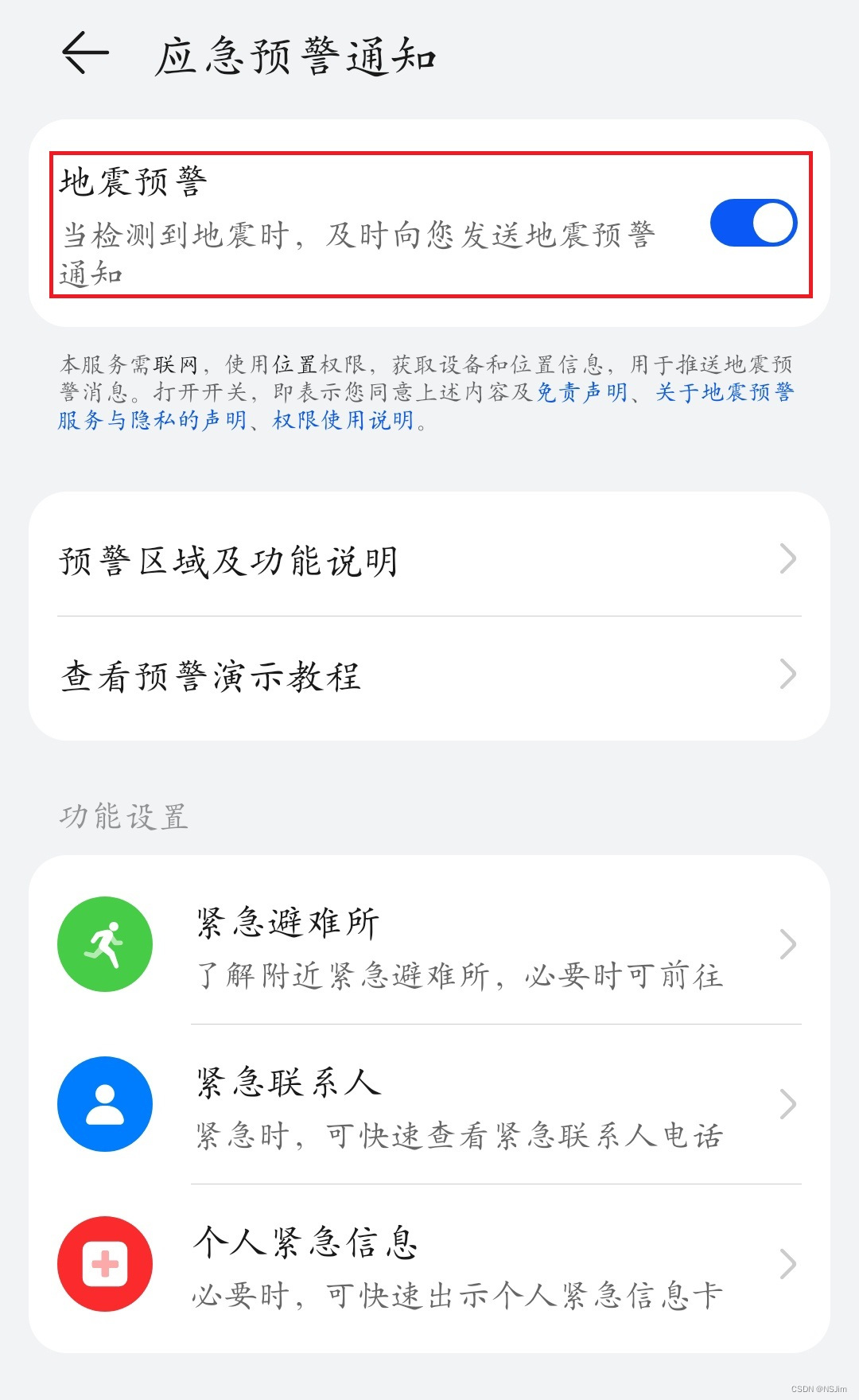
手机开启应急预警通知 / 地震预警
前言 安卓手机在检测到地震时,将发送地震预警通知,但此设置是默认关闭的,原因是以防引发用户恐慌从而引发安全问题,且开启此设置需要完成指引教程,因此默认关闭此设置。下文介绍如何开启此设置。 开启方法 华为手机开…...

2020年12月 Python(一级)真题解析#中国电子学会#全国青少年软件编程等级考试
一、单选题(共25题,每题2分,共50分) 第1题 执行语句print(10==10.0)的结果为? A:10 B:10.0 C:True D:False 正确的答案是 C:True。 解析:在Python中,比较运算符 “==” 用于比较两个值是否相等。在这个特定的比较中,整数10和浮点数10.0在数值上是相等的。…...

遇到无法复现的 Bug
当我们在软件开发过程中遇到无法复现的 Bug 时,这可能会让我们感到头疼和困惑。处理这种 Bug 需要一些技巧和方法来帮助我们更好地解决问题。本篇博客将为大家总结一些常用的技术手段和策略,希望能对开发者们在日常工作中遇到类似问题时提供一些帮助。 …...
)
虚拟列表的实现(简单易懂)
起因: app开发过程中遇到需要渲染3000行的列表,页面直接卡顿,所以开始研究起虚拟列表 实现前提条件: item项等高列表 实现思路: 首先是dom结构: 定义一个容器(固定高度)&#…...

【WordPress】如何在WordPress中实现真·页面路由
这篇文章也可以在我的博客中查看 页面路由 是什么 页面路由是指从url顺着网线砍到网站内容的途径,说人话就是地址与页面的映射。 就像真实世界的地址一样,我要找你,必须知道你的地址。 在网站中,通过地址找内容的机制…...
Android界面设计与用户体验
Android界面设计与用户体验 1. 引言 在如今竞争激烈的移动应用市场,提供优秀的用户体验成为了应用开发的关键要素。无论应用功能多么强大,如果用户界面设计不合理,用户体验不佳,很可能会导致用户流失。因此,在Androi…...
:音画同步)
基于 FFmpeg 的跨平台视频播放器简明教程(八):音画同步
系列文章目录 基于 FFmpeg 的跨平台视频播放器简明教程(一):FFMPEG Conan 环境集成基于 FFmpeg 的跨平台视频播放器简明教程(二):基础知识和解封装(demux)基于 FFmpeg 的跨平台视频…...
)
【NLP pytorch】基于BiLSTM-CRF模型医疗数据实体识别实战(项目详解)
基于BiLSTM-CRF模型医疗数据实体识别实战 1数据来源与加载1.1 数据来源1.2 数据类别名称和定义1.3 数据介绍2 模型介绍2 数据预处理2.1 数据读取2.2 数据标注2.3 数据集划分2.4 词表和标签的生成3 Dataset和DataLoader3.1 Dataset3.2 DataLoader4 BiLSTM模型定义5 CRF模型6 模型…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
