两个状态的马尔可夫链
手动推导如下公式。

证明:
- 首先将如下矩阵对角化:
{ 1 − a a b 1 − b } \begin {Bmatrix} 1-a & a \\ b & 1-b \end {Bmatrix} {1−aba1−b}
(1)求如下矩阵的特征值:
{ 1 − a a b 1 − b } { x 1 x 2 } = λ { x 1 x 2 } = = > \begin {Bmatrix} 1-a & a \\ b & 1-b \end {Bmatrix} \begin {Bmatrix} x_1 \\x_2 \end {Bmatrix} = \lambda \begin {Bmatrix} x_1 \\x_2 \end {Bmatrix} == > {1−aba1−b}{x1x2}=λ{x1x2}==>
∣ 1 − a − λ a b 1 − b − λ ∣ = 0 = = > \begin {vmatrix} 1-a - \lambda& a \\ b & 1-b - \lambda \end {vmatrix} = 0 ==> 1−a−λba1−b−λ =0==>
( 1 − a − λ ) ( 1 − b − λ ) − a b = 0 = = > (1-a- \lambda)(1-b - \lambda) - ab = 0 ==> (1−a−λ)(1−b−λ)−ab=0==>
λ 2 + ( a + b − 2 ) λ + ( 1 − a − b ) = 0 = = > λ = ( 2 − a − b ) + − ( a + b − 2 ) 2 − 4 ( 1 − a − b ) 2 = ( 2 − a − b ) + − ( a + b ) 2 = ( 1 ) o r ( 1 − a − b ) \lambda^2 +(a+b-2)\lambda + (1-a-b) = 0 ==> \\ \lambda = \frac{(2-a-b) +- \sqrt{(a+b-2)^2-4(1-a-b)}}{2} = \\ \frac{(2-a-b) +- (a+b)}{2} = (1) or (1-a-b) λ2+(a+b−2)λ+(1−a−b)=0==>λ=2(2−a−b)+−(a+b−2)2−4(1−a−b)=2(2−a−b)+−(a+b)=(1)or(1−a−b)
(2)求得正交特征向量
∣ − a a b − b ∣ ∣ x 1 x 2 ∣ = 0 = = > x 1 = 1 , x 2 = 1 \begin {vmatrix} -a & a \\ b &-b \end {vmatrix} \begin {vmatrix} x_1 \\x_2 \end {vmatrix} = 0 ==> x_1 = 1,x_2 = 1 −aba−b x1x2 =0==>x1=1,x2=1
∣ b a b a ∣ ∣ x 1 x 2 ∣ = 0 = = > x 1 = a , x 2 = − b \begin {vmatrix} b & a \\ b &a \end {vmatrix} \begin {vmatrix} x_1 \\x_2 \end {vmatrix} = 0 ==> x_1 = a,x_2 = -b bbaa x1x2 =0==>x1=a,x2=−b
也即:
A = P − 1 Λ P = { 1 2 a a 2 + b 2 1 2 − b a 2 + b 2 } { 1 0 0 1 − a − b } { 1 2 1 2 a a 2 + b 2 − b a 2 + b 2 } A = P^{-1} \Lambda P = \begin {Bmatrix} \frac{1}{\sqrt{2}} & \frac{a}{\sqrt{a^2+b^2}} \\\\ \frac{1}{\sqrt{2}} & \frac{-b}{\sqrt{a^2+b^2}} \end {Bmatrix} \begin {Bmatrix} 1 & 0\\\\ 0& 1 - a - b \end {Bmatrix} \begin {Bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \\ \frac{a} {\sqrt{a^2+b^2}} & \frac{-b}{\sqrt{a^2+b^2}} \end {Bmatrix} A=P−1ΛP=⎩ ⎨ ⎧2121a2+b2aa2+b2−b⎭ ⎬ ⎫⎩ ⎨ ⎧1001−a−b⎭ ⎬ ⎫⎩ ⎨ ⎧21a2+b2a21a2+b2−b⎭ ⎬ ⎫
A n = P − 1 Λ n P = { 1 2 a a 2 + b 2 1 2 − b a 2 + b 2 } { 1 0 0 ( 1 − a − b ) n } { 1 2 1 2 a a 2 + b 2 − b a 2 + b 2 } = { 1 2 + a 2 ( 1 − a − b ) 2 a 2 + b 2 1 2 + − a b ( 1 − a − b ) 2 a 2 + b 2 1 2 + − a b ( 1 − a − b ) 2 a 2 + b 2 1 2 + b 2 ( 1 − a − b ) 2 a 2 + b 2 } A^n = P^{-1} \Lambda^n P = \begin {Bmatrix} \frac{1}{\sqrt{2}} & \frac{a}{\sqrt{a^2+b^2}} \\\\ \frac{1}{\sqrt{2}} & \frac{-b}{\sqrt{a^2+b^2}} \end {Bmatrix} \begin {Bmatrix} 1 & 0\\\\ 0& (1 - a - b)^n \end {Bmatrix} \begin {Bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \\ \frac{a} {\sqrt{a^2+b^2}} & \frac{-b}{\sqrt{a^2+b^2}} \end {Bmatrix} =\\ \\ \begin {Bmatrix} \frac{1}{2} + \frac{a^2 (1-a-b)^2}{a^2+b^2} & \frac{1}{2} + \frac{-ab (1-a-b)^2}{a^2+b^2} \\\\ \frac{1}{2} + \frac{-ab (1-a-b)^2}{a^2+b^2} & \frac{1}{2} + \frac{b^2 (1-a-b)^2}{a^2+b^2} \end {Bmatrix} An=P−1ΛnP=⎩ ⎨ ⎧2121a2+b2aa2+b2−b⎭ ⎬ ⎫⎩ ⎨ ⎧100(1−a−b)n⎭ ⎬ ⎫⎩ ⎨ ⎧21a2+b2a21a2+b2−b⎭ ⎬ ⎫=⎩ ⎨ ⎧21+a2+b2a2(1−a−b)221+a2+b2−ab(1−a−b)221+a2+b2−ab(1−a−b)221+a2+b2b2(1−a−b)2⎭ ⎬ ⎫
相关文章:

两个状态的马尔可夫链
手动推导如下公式。 证明: 首先将如下矩阵对角化: { 1 − a a b 1 − b } \begin {Bmatrix} 1-a & a \\ b & 1-b \end {Bmatrix} {1−aba1−b} (1)求如下矩阵的特征值: { 1 − a a b 1 − b } { x 1 x 2 } λ { x 1 x 2 }…...

SpringBoot 依赖管理
Spring Boot 依赖管理 1. 父项目做依赖管理 无需关注版本号,自动版本仲裁机制 <!-- 依赖管理 --> <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version&g…...
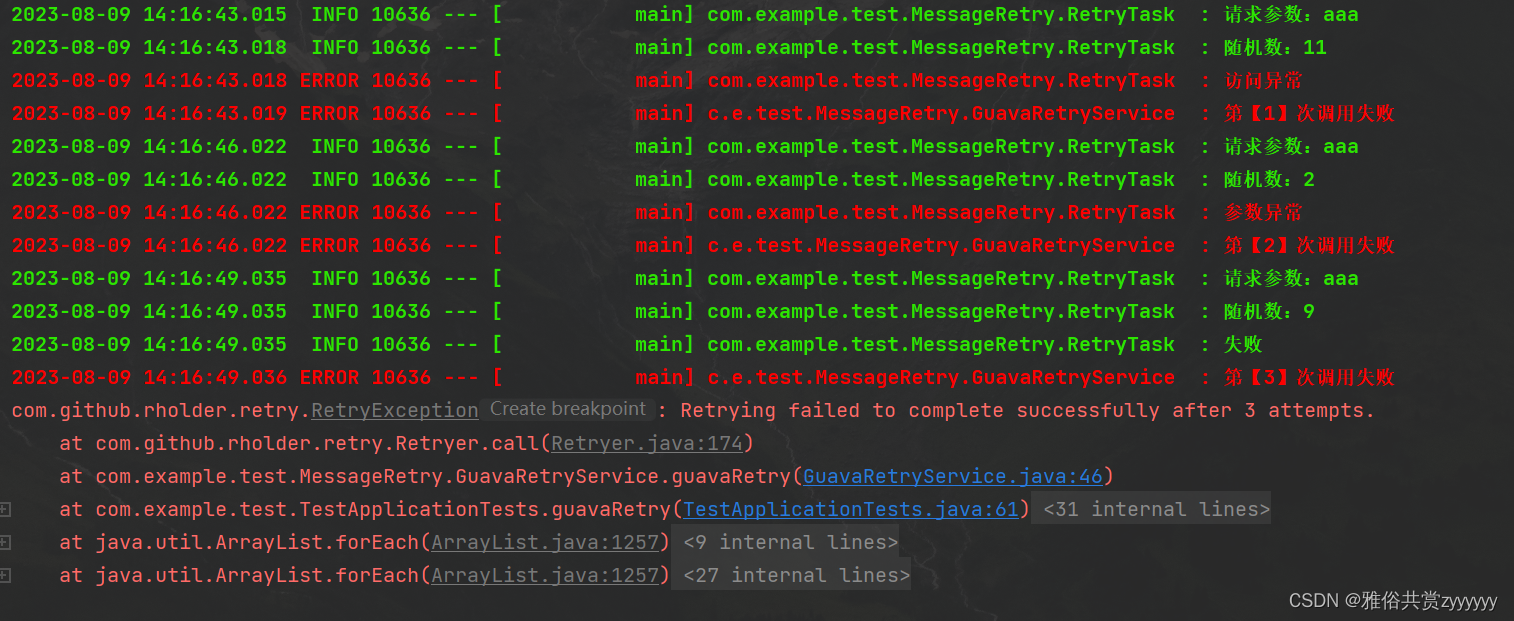
重试框架入门:Spring-RetryGuava-Retry
前言 在日常工作中,随着业务日渐庞大,不可避免的涉及到调用远程服务,但是远程服务的健壮性和网络稳定性都是不可控因素,因此,我们需要考虑合适的重试机制去处理这些问题,最基础的方式就是手动重试…...

[QCM6125][Android13] 修复PRODUCT_COPY_FILES无法拷贝so
文章目录 开发平台基本信息问题描述解决方法 开发平台基本信息 芯片: QCM6125 版本: Android 13 kernel: msm-4.14 问题描述 在进行系统移植时,经常会把一些自己开发的c或者c程序编译成so库,然后在系统服务中去调用这些库。所以在进行新代码开发时&am…...
微服务Eureka注册中心
目录 一、Eureka的结构和作用 二、搭建eureka-server 三、服务注册 四、服务发现 假如我们的服务提供者user-service部署了多个实例,如图: 存在的问题: order-service在发起远程调用的时候,该如何得知user-service实例的ip地址…...

Java:企业级java后端开发,需要掌握哪些内容
一、什么是后端开发 后端开发是指开发基于服务器端的软件应用程序,也称为系统的后台或服务器端编程。 后端程序员负责处理网站或应用程序后台的逻辑和功能,包括数据库管理、服务器端脚本编写、API设计、数据安全性、网站性能优化等。 后端开发技术通常包…...
)
使用Go语言生成Excel任务表依赖图(Markdown文件mermaid图)
一、前言 在游戏中,任务是非常常见的玩法,可能会有主线任务,支线任务以及其它一些类型的任务,各任务可能还会有前置任务,即需要完成某个任务之后,才能做当前任务。在游戏开发中,配置表可以使用…...

C语言和C++的区别在哪?如何自学C++?
C语言和C是两种不同的编程语言,它们在语法、特性和用途上有一些区别。以下是C语言和C的一些主要区别: 面向对象编程:C是一种支持面向对象编程的语言,它在C语言的基础上添加了类、对象、继承、多态等面向对象的特性。而C语言是一种…...

功能强大的开源数据中台系统 DataCap 1.13.0 发布
推荐一套基于 SpringBoot 开发的简单、易用的开源权限管理平台,建议下载使用: https://github.com/devlive-community/authx 推荐一套为 Java 开发人员提供方便易用的 SDK 来与 OpenAI 的 API 进行交互组件:https://github.com/devlive-community/openai…...
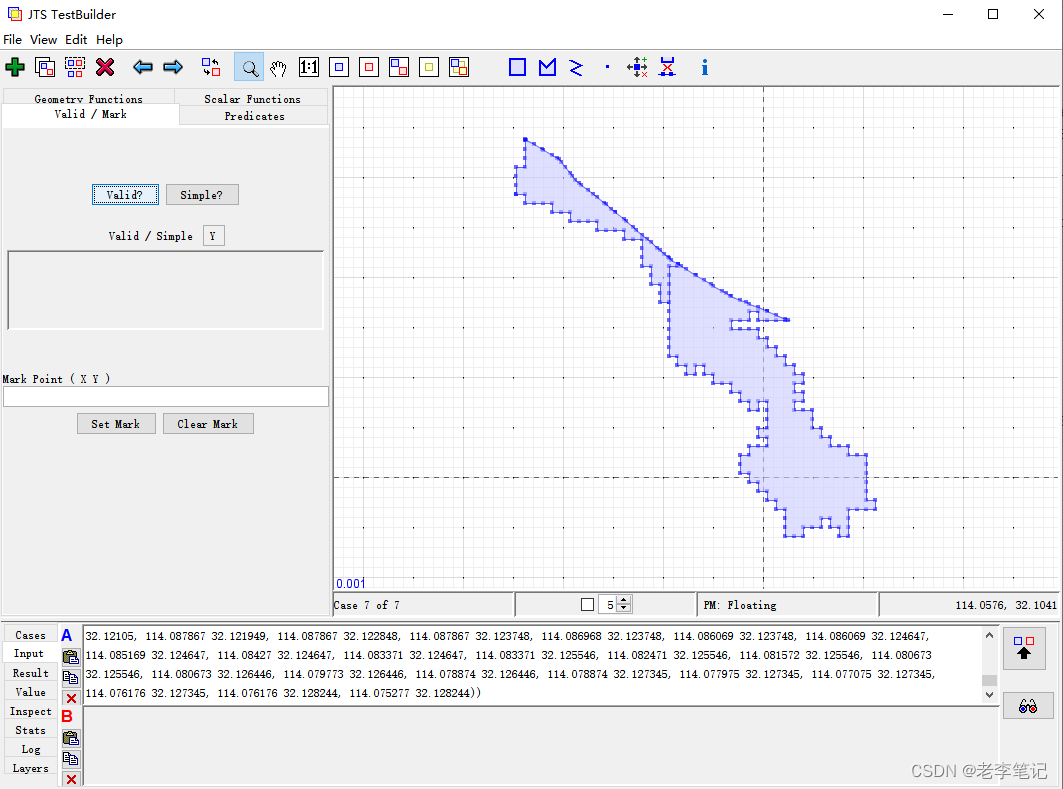
JTS Self-intersection异常TopologyException: side location conflict解决办法
JTS Self-intersection异常TopologyException: side location conflict解决办法 举例:问题围栏 MULTIPOLYGON (((114.0905685 32.1120567, 114.0905685 32.112957, 114.0905685 32.1138535, 114.0905685 32.1147537, 114.0905685 32.115654, 114.0905685 32.11655…...
Maven: No compiler is provided in this environment.
在Eclipse中运行Maven项目,报错: No compiler is provided in this environment. Perhaps you are running on a JRE rather than a JDK? 解决方法: Windows > Preferences > Java > Installed JREs > Add > Standard VM,…...

.NET-10. 其他-VSTO+VBA
VSTOVBA 前言VSTO 外接程序介绍:VSTO参考链接:VSTO 例子: VBA:参考链接: 前言 主要用于Excel插件。 VSTO 外接程序介绍: Excel、Word、PowerPoint、Project、Visio等等Office应用程序 相对简单 VSTO参考链接&#x…...
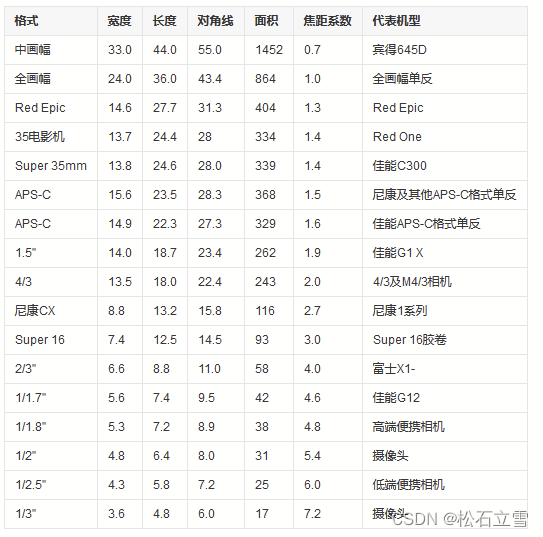
相机传感器格式与镜头光圈参数
相机靶面大小 CCD/CMOS图像传感器尺寸(sensor format)1/2’‘、1/3’‘、1/4’实际是多大 1英寸——靶面尺寸为宽12.7mm*高9.6mm,对角线16mm。 2/3英寸——靶面尺寸为宽8.8mm*高6.6mm,对角线11mm。 1/2英寸——靶面尺寸为宽6.…...
)
Android 设置头像(拍照获取、相册获取、裁剪照片)
在Android原生态开发过程中,往往会设计到用户头像的设置问题,一般来讲设置头像需要用到拍照、获取照片、存储照片、裁剪照片、显示照片等问题,本文将一步一步的进行说明讲解。 首先需要强调几点我在开发过程中遇到的问题。 权限问题…...
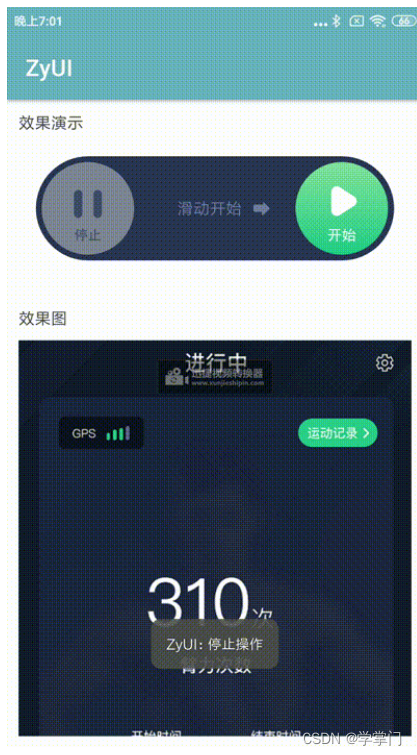
android开发之Android 自定义滑动解锁View
自定义滑动解锁View 需求如下: 近期需要做一个类似屏幕滑动解锁的功能,右划开始,左划暂停。 需求效果图如下 实现效果展示 自定义view如下 /** Desc 自定义滑动解锁View Author ZY Mail sunnyfor98gmail.com Date 2021/5/17 11:52 *…...
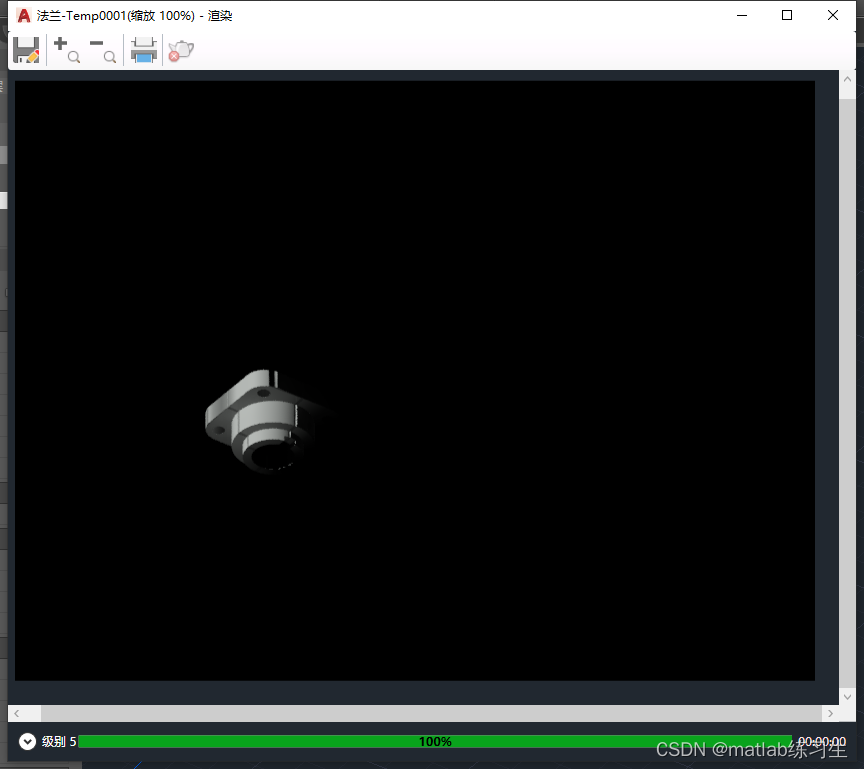
CAD绘制法兰、添加光源、材质并渲染
首先绘制两个圆柱体,相互嵌套 在顶部继续绘制圆柱体,这是之后要挖掉的部分 在中央位置绘制正方形 用圆角工具: 将矩形的四个角分别处理,效果: 用拉伸工具 向上拉伸到和之前绘制的圆柱体高度齐平 绘制一个圆柱体&#…...

ChatGPT访问流量下降的原因分析
自从OpenAI的ChatGPT于11月问世以来,这款聪明的人工智能聊天机器人就席卷了全世界,人们在试用该工具的同时也好奇该技术到底将如何改变我们的工作和生活。 但近期Similarweb表示,自去ChatGPT上线以来,该网站的访问量首次出现下…...

干货 | 详述 Elasticsearch 向量检索发展史
1. 引言 向量检索已经成为现代搜索和推荐系统的核心组件。 通过将复杂的对象(例如文本、图像或声音)转换为数值向量,并在多维空间中进行相似性搜索,它能够实现高效的查询匹配和推荐。 图片来自:向量数据库技术鉴赏【上…...

mysql常见面试题,高频题目放送
互联网的产品架构是包含这接入层,逻辑处理以及储存层的,其中储存层承载着较多的数据以及持久化的任务,而说到储存层,避免不了说到数据库,在我们面试的时候,数据库的知识题目占比是非常多的: 1.…...
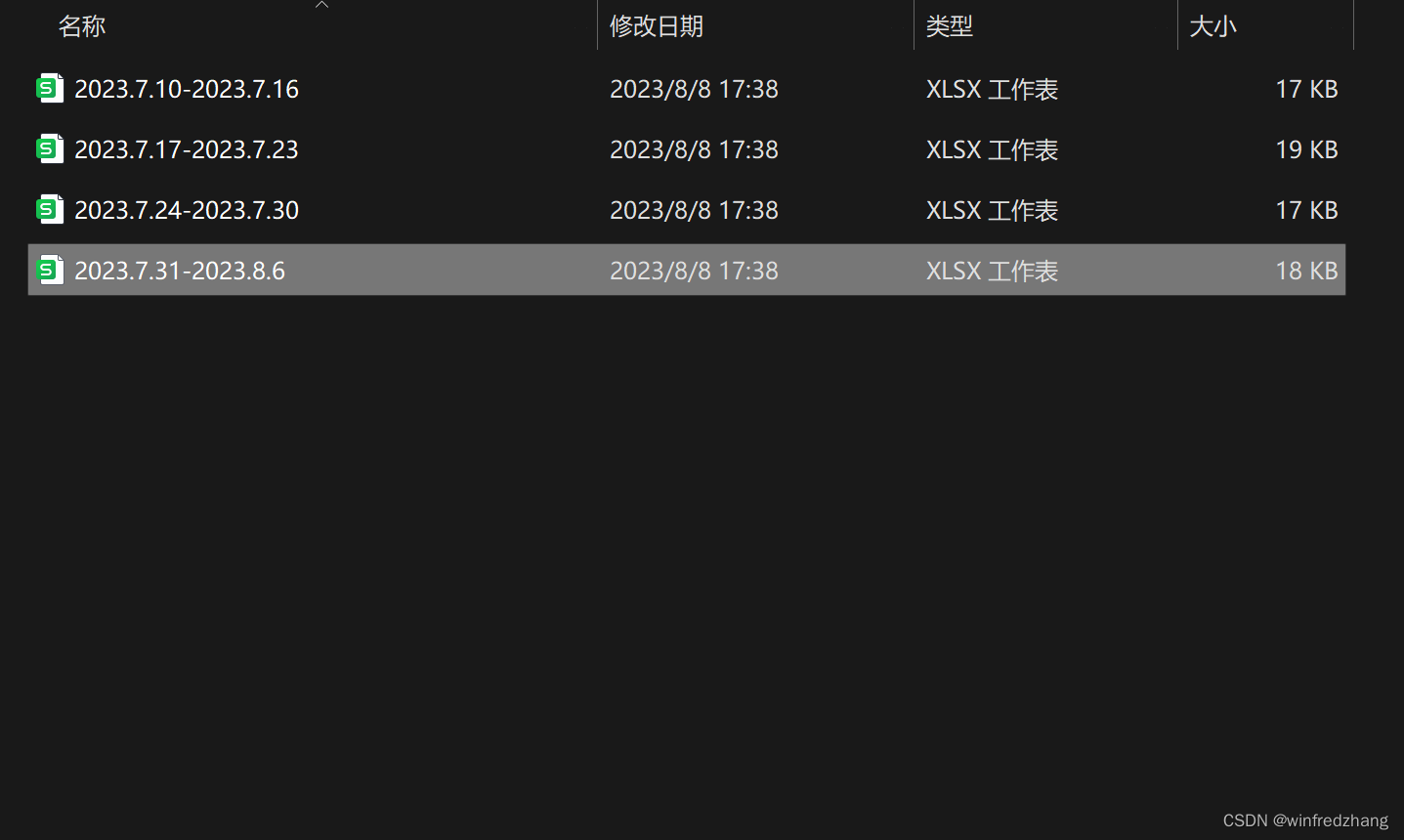
使用 PowerShell 将 Excel 中的每个工作表单独另存为独立的文件
导语:在日常工作中,我们经常需要处理 Excel 文件。本文介绍了如何使用 PowerShell 脚本将一个 Excel 文件中的每个工作表单独另存为独立的 Excel 文件,以提高工作效率。 1. 准备工作 在开始之前,请确保已经安装了 Microsoft Exc…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
