leetcode357- 2812. 找出最安全路径
这个题比较经典,可以用多个算法来求解,分别给出各个算法的求解方法,主要是分为第一部分的多源BFS求每个位置的距离和第二部分求(0,0)到(n-1,n-1)的最短路径(可以用多种方法求)
目录
- 多源BFS
- 求最短路径
- 枚举安全系数判断是否可行
- 枚举安全系数
- 路径是否存在
多源BFS
首先是要求得每个点距离最近的小偷所在位置的距离长度:
暴力枚举每个小偷所在位置,更新所有点到该小偷位置的距离,数据量为400,假设每个位置都有小偷,小偷数量达到400*400,再加上枚举每个位置,最后的复杂度为O(400 * 400 * 400 * 400),即O(n^4)会超时;
多源BFS求距离:多源BFS
// 以所有小偷为起点进行多源 bfsmemset(dis, -1, sizeof(dis));for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) if (grid[i][j] == 1) {q.push(pii(i, j));dis[i][j] = 0;}while (!q.empty()) {pii p = q.front(); q.pop();int i = p.first, j = p.second;for (int k = 0; k < 4; k++) {int ii = i + dir[k][0], jj = j + dir[k][1];if (ii < 0 || jj < 0 || ii >= n || jj >= m || dis[ii][jj] >= 0) continue;q.push(pii(ii, jj));dis[ii][jj] = dis[i][j] + 1;}}
求最短路径
枚举安全系数判断是否可行
枚举答案看是否存在满足答案的路径。
这个思路采用逆向思维方式,不是枚举最短路径判断安全系数,而是枚举安全系数判断对应的最短路径是否存在,也是分为两部分,一部分是如何枚举安全系数,另一部分是如何判断只经过安全系数为lim并且连通起点到终点的路径是否存在。
枚举路径中安全系数(经过的格子的最小值)可以是哪些,相当于枚举只经过安全系数为lim的路径,路径中经过的格子安全系数全都大于等于lim,能否从起点到达终点;然后让这个lim尽可能地大。
枚举安全系数
- 可以直接从最大的开始枚举,找到一个符合条件的就可以结束了,O(n)
//直接从大到小枚举for(int i=min(dis[0][0],dis[n-1][m-1]);i>=0;i--){if(check(i)) return i;}
- 二分枚举, O(logn) 【最小值最大或者是最大值最小问题】
//二分int l=0,r=min(dis[0][0],dis[n-1][m-1]);while(l<r){int mid=(l+r+1)>>1;if(check(mid)) l=mid;else r=mid-1;}
路径是否存在
判断路径上的安全系数为lim,也就是之前求出来的所有节点的值大于等于lim的连接起点到终点的路径是否存在,有多种方法,bfs,dfs,并查集,只要判断起点和终点连通就行。
- BFS
bfs检查时间,每个位置处遍历一次,复杂度为O(n^2)
//通过一次bfs,检查能否只经过安全系数大于等于lim的格子,从左上角走到右下角bool check(int lim){q.push({0,0});memset(visited, 0, sizeof(visited));visited[0][0]=true;while(!q.empty()){pii p = q.front(); q.pop();int i = p.first, j = p.second;for (int k = 0; k < 4; k++) {int ii = i + dir[k][0], jj = j + dir[k][1];if (ii < 0 || jj < 0 || ii >= n || jj >= m || dis[ii][jj]<lim ||visited[ii][jj]) continue;q.push(pii(ii, jj));visited[ii][jj]=true;}}return visited[n-1][n-1];}
-
DFS
深搜不行,因为涉及到回溯,导致每个节点可能访问多次,导致深搜的时间复杂度无法控制在O(n^2)内,会超时。 -
并查集判断(0,0)和(n-1,n-1)是否连通
int find(int x){if(p[x]==x) return x;return p[x]=find(p[x]);}//并差集判断bool check(int lim){//初始化并查集每个元素是自己,将二维的数组拉成一维的int x=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){p[x]=x;x++; }}//将每个节点与周围节点合并for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(dis[i][j]<lim) continue;int a=find(i*n+j);for (int k = 0; k < 4; k++) {int ii = i + dir[k][0], jj = j + dir[k][1];if (ii < 0 || jj < 0 || ii >= n || jj >= m || dis[ii][jj]<lim ) continue;int b =find(ii*n+jj);if(a!=b) p[b]=a; //合并}}}return find(0)==find(n*n-1) ;}
相关文章:

leetcode357- 2812. 找出最安全路径
这个题比较经典,可以用多个算法来求解,分别给出各个算法的求解方法,主要是分为第一部分的多源BFS求每个位置的距离和第二部分求(0,0)到(n-1,n-1)的最短路径(可以用多种方法求) 目录 多源BFS求最短路径枚举安全系数判断…...
Oracle连接数据库提示 ORA-12638:身份证明检索失败
ORA-12638 是一个 Oracle 数据库的错误代码,它表示身份验证(认证)检索失败。这通常与数据库连接相关,可能由于以下几个原因之一引起: 错误的用户名或密码: 提供的数据库用户名或密码不正确,导致…...

在 Linux 中使用 systemd 注册服务
Systemd 是一种现代的 Linux 系统初始化系统和服务管理器。它旨在管理系统服务的初始化、配置和控制。Systemd 的一个关键特性是它可以管理服务,这些服务是为系统提供特定功能的后台进程。在本指南中,我们将探讨如何使用 systemd 在 Linux 中注册服务。 …...

(03)Unity HTC VRTK 基于 URP 开发记录
1.简介 本篇主要内容为:URP如何与VRTK结合、URP需要注意的地方、VRTK的功能进行阐述。 因项目本身要求要渲染出比较好的画质,所以抛弃了Unity默认渲染管线Built-in,使用URP进行渲染,当然也可以选HDRP,但考虑到后期项目…...
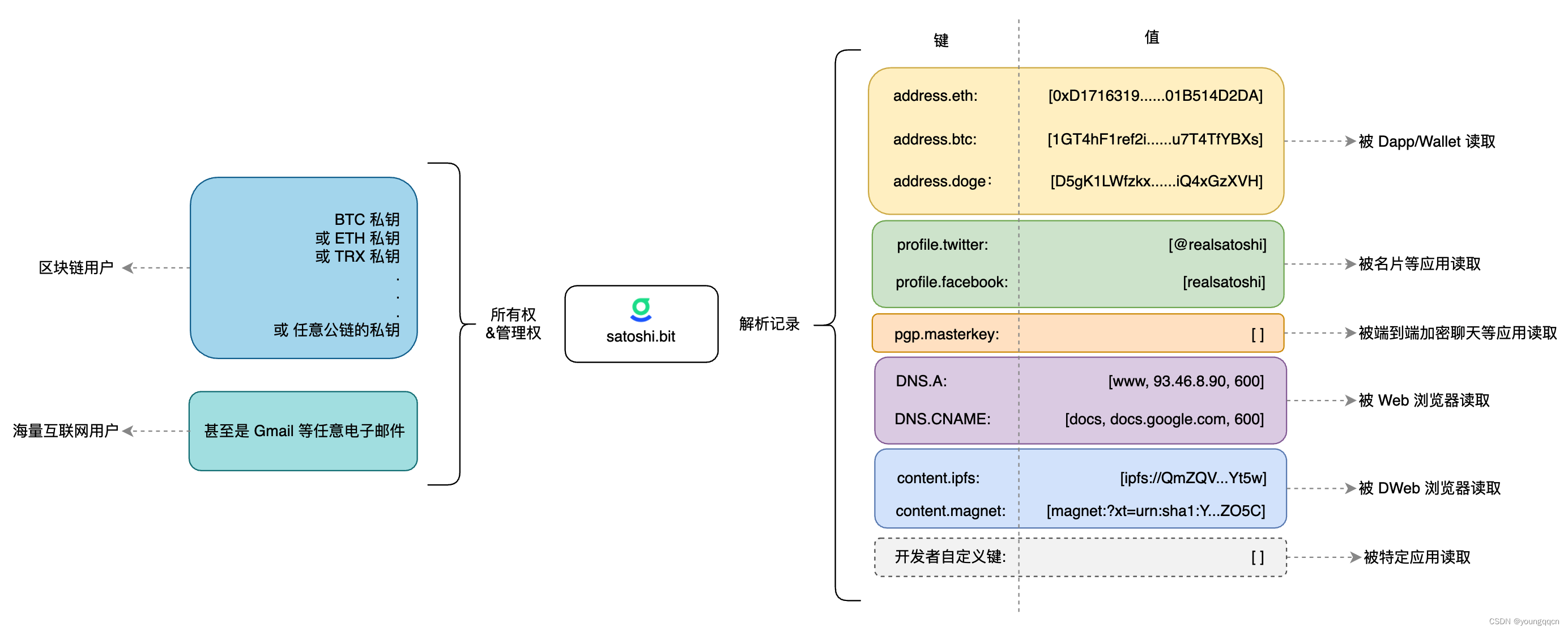
.bit域名调研
.bit域名研究 问题: .bit域名和ENS域名的相同点?不同点?有什么关系? .bit的定义 .bit 是基于区块链的,开源的,跨链去中心化账户系统.bit 提供了以 .bit 为后缀的全局唯一的命名体系,可用于加密…...
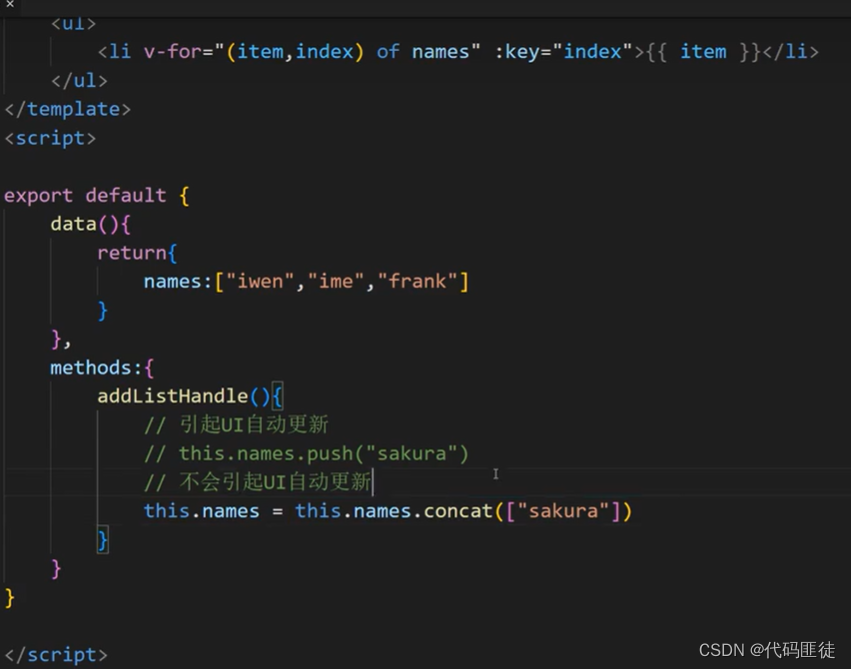
Vue数组变更方法和替换方法
一、可以引起UI界面变化 Vue 将被侦听的数组的变更方法进行了包裹,所以它们也将会触发视图更新。这些被包裹过的方法包括: push()pop()shift()unshift()splice()sort()reverse() 以上七个数组都会改变原数组,下面来分别讲解它们的区别&…...

Centos-6.3安装使用MongoDB
安装说明 系统环境:Centos-6.3 安装软件:mongodb-linux-x86_64-2.2.2.tgz 下载地址:http://www.mongodb.org/downloads 安装机器:192.168.15.237 上传位置:/usr/local/ 软件安装位置:/usr/local/mongodb 数…...

Mysql 复杂查询丨联表查询
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! JOIN(联表查询) 联表查询(Join)是一种在数据库中使用多个表进行关联查询的操作。它通过使用 JOIN 关键字将多个表连接在…...
C语言进阶第二课-----------指针的进阶----------升级版
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...

若依vue -【 111 ~ 更 ~ 127 完 】
【更】111 3.5.0版本更新介绍 112 使用docker实现一键部署 1、安装docker yum install https://download.docker.com/linux/fedora/30/x86_64/stable/Packages/containerd.io-1.2.6-3.3.fc30.x86_64.rpm yum install -y yum-utils device-mapper-persistent-data lvm2 yum-c…...
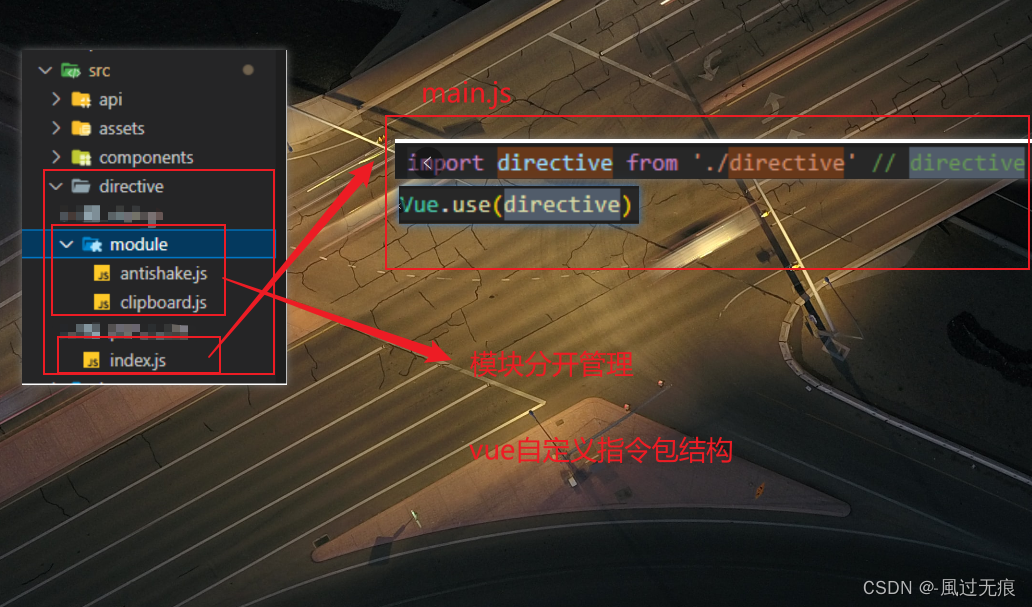
vue-pc端实现按钮防抖处理-自定义指令
前言 我们经常在移动端会处理按钮和输入框的防抖和节流处理,在pc端很少进行这样的操作 但是在pc端也是可以进行按钮的防抖操作,这样也是比较合理,可以不用但不可以不会 我们只要配合vue项目自定义指令加上全局注册,就可以实现按…...

python解决8皇后问题
def is_valid(queens, row, col):for i in range(row):if queens[i] == col or abs(queens[i] - col) == abs(i - row):return Falsereturn Truedef solve_n_queens(n, row, queens, result):if row == n:result.append(queens[:]) # 将当前解添加到结果中returnfor col in ra…...

xcode打包导出ipa
转载:xcode打包导出ipa 目录 转载:xcode打包导出ipa 第一步:注册苹果开发者账号 第二步:下载APP Uploader 第三步:使用xcode打包导出ipa文件,供其他人内测 众所周知,在开发苹果应用时需要使…...

更优雅地调试SwiftUI—借助LLDB
更优雅地调试SwiftUI—借助LLDB 概述 你是否写过这样的代码: struct ContentView: View {@State private var mySize: CGFloat = 15.0var myString: String = "Hi LLDB"var myArray: [Int] = [1, 2, 3]var body: some View {VStack {Text("Hello World"…...

2.4 网络安全新技术
数据参考:CISP官方 目录 云计算安全大数据安全移动互联网安全物联网安全工业互联网安全 一、云计算安全 1、云计算定义 云计算是指通过网络访问可扩展的、灵活的物理或虚拟共享资源池,并按需自助获取和管理资源的模式。在云计算中,计算资…...

人生天地之间,若白驹之过隙,忽然而已
人生天地之间,若白驹之过隙,忽然而已 这段时间有个同事离职了,其实身边不断有老人走、有新人来,但这回走的同事和别的有些不同,当时我入职面试的时候就是他面试的我,工作中有啥问题都会请教他,…...
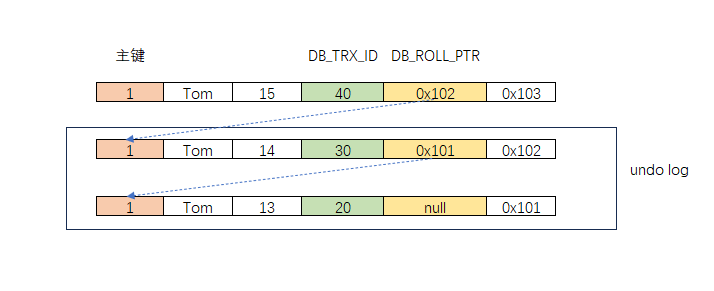
MySQL — MVCC
文章目录 MVCCMVCC 实现原理隐藏字段undo logundo log的用途undo log类型 版本链ReadView MVCC InnoDB是一个多版本的存储引擎。它保留有关已更改行的旧版本的信息,以支持并发和回滚等事务性特性。这些信息存储在undo表空间中的数据结构称为回滚段。InnoDB使用回滚…...
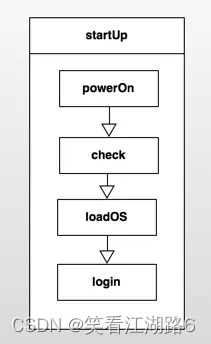
Android模板设计模式之 - 构建整个应用的BaseActivity
1. 模式介绍 模式的定义 定义一个操作中的算法的框架,而将一些步骤延迟到子类中。使得子类可以不改变一个算法的结构即可重定义该算法的某些特定步骤。 模式的使用场景 1.多个子类有公有的方法,并且逻辑基本相同时。 2.重要、复杂的算法,可…...

浏览器缓存技术--localStorage和sessionStorage原理与使用
localStorage和sessionStorage LocalStorageLocalStorage的特点存入/读取数据使用场景 sessionStoragesessionStorage的特点存入/读取数据使用场景sessionStorage 、localStorage 和 cookie 之间的区别 测试localStorage和sessionStorageIndexedDB LocalStorage 为了弥补 Cook…...

无涯教程-Perl - endservent函数
描述 此功能告诉系统您不再期望使用getservent从服务文件中读取条目。 语法 以下是此函数的简单语法- endservent返回值 此函数不返回任何值。 例 以下是显示其基本用法的示例代码- #!/usr/bin/perlwhile(($name, $aliases, $port_number,$protocol_name)getservent())…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
