Nim游戏:取石头
(一)一堆取石头
背景:
在博弈论中,有一种称为Nim游戏的经典问题,它涉及到取石子的问题,其中有许多变种。Nim游戏是一种零和博弈,即两名玩家交替行动,每次只能从一堆物品中取走一定数量的物品,无法分割物品。
题目中描述的场景是这样的:
有n个石头,两名玩家轮流进行操作,每次可以从石头堆中取走1到m个石头(其中m是一个固定的正整数)。玩家可以根据自己的策略选择取多少个石头,目标是使自己取得最后一个石头。
题解思路:
令 ans = n%(m+1)(为什么这样令,后面会讲解)
判断是否存在先手必胜策略这一问题,即可一开始检验石子堆中的ans是否为0,当ans为0时,你面对的是ans==0的局面,你的任意操作都会使得当前ans不为0,你的对手又足够聪明,那你每执行一步,他都会再次把ans==0的局面返还给你,那你最后必输;
当ans不为0时,你先手,你又足够聪明,你每次执行后都可以把ans==0的局面留给对手,最后你必胜。
-
为什么令 ans = n%(m+1)?
当先手玩家取石头使石头个数 n 能够被(m+1)整除时,后手玩家所要面临的情况是:无论怎么取都不可能取完石头。如果先手玩家能够保证后手玩家一直面临石头个数 n 能够被(m+1)整除,那么最后一次,后手玩家面临的情况是:石头的个数是 m+1,所以后手玩家无论怎么取都不可能取完石头,最后只能是先手玩家将石头取完。
所以对于自己来说,取胜的条件是:自己面临的石头个数情况是 n%(m+1)!= 0;然后自己取石头使石头个数能够被(m+1)整数。
(二)多堆取石头:
这里我转载一位大佬的博客:博弈论石子游戏——nim 游戏_[模板]nim游戏_Wu_L7的博客-CSDN博客
题目描述:
地上有 n 堆石子(每堆石子数量小于 10^4),每人每次可从任意一堆石子里取出任意多枚石子扔掉,可以取完,不能不取。每次只能从一堆里取。最后没石子可取的人就输了。假如甲是先手,且告诉你这 n 堆石子的数量,他想知道是否存在先手必胜的策略。
题目思路:
必胜策略,即当你执行最后一步后,你的对手已无石子可取,他必败你必胜。最后局面是地上各个石子堆已无石子可取,假设 ai 代表第 i 个石子堆中的石子数,则 ai = 0(i ≤ n)。即可得,a1^a2^a3^……^an=0(^表示异或),令ans = a1^a2^a3^……^an,要想必胜,说明最后的局面一定是ans==0,那我只需要满足,我每次操作完使得ans==0即可,那么每次留给对手的局面都是ans==0(怎么实现后面讲),并且石子的初始数确定,每次都取走一部分的石子,在有限的步数内肯定会取完,当执行到最后一步ans==0时,恰好最后的石子被你取完,你必胜。
那么,判断是否存在先手必胜策略这一问题,即可一开始检验石子堆中的ans是否为0,当ans为0时,你面对的是ans==0的局面,你的任意操作都会使得当前ans不为0,你的对手又足够聪明,那你每执行一步,他都会再次把ans==0的局面返还给你,那你最后必输;当ans不为0时,你先手,你又足够聪明,你每次执行后都可以把ans==0的局面留给对手,最后你必胜。
小tip:
为什么每次操作之后都会使得ans==0转化成ans != 0,并且足够聪明的你执行完一次操作之后又能把ans != 0变成ans==0?
1、ans==0执行一次操作之后为什么会转化为ans != 0?
异或,即是把每个ai中转化为二进制的形式,再对每一个位置的所有0和1进行异或操作,举个例子:5^3=6(0101^0011=0110)。而ans = a1^a2^a3^……^an,每次只能对一个石子堆操作,即每次操作只会影响ai(i ≤ n)中的一个,假设是对ak进行操作,则(没操作前的ak)^(其它ai的异或)==0,说明(其它ai的异或)==(没操作前的ak)(因为两个相同的数相异或结果才为0),现在对ak进行操作,则ak的值肯定会变化,其二进制形式也随之变化,则(操作后的ak)!=(其它ai的异或),所以(操作后的ak)^(其它ai的异或)!= 0,则ans != 0。
2、为什么足够聪明的你执行完一次操作之后又能把ans != 0变成ans==0?
ans = a1^a2^a3^……^an,是各个位置多个0和1的异或,因为ans != 0,说明一定有个别位置中1的个数为奇数,则我们可以把该位置上的1去掉一个或增加一个,即取走一些石头,使之为偶数,则ans==0。例如:10^5=15(1010^0101=1111),这是最经典的了,我们可以从10中拿走5,则5^5=0,所以想说明的是,总有办法使ans==0。
注:
这里有个简单的取石头个数的技巧(异或的简单计算方法):
例如:7和14的异或
7的二进制序列为: 0111
14的二进制序列为:1110
则异或结果是:1001 == 9
简便计算:
7可以写成2的倍数之和:4+2+1
14可以写成2的倍数之和:8+4+2+0
然后约去两部分相同的部分:7剩余一个1;14剩余一个8,再将剩余的数相加,其结果就是异或结果9。
本次内容到此结束了!如果你觉得这篇博客对你有帮助的话 ,希望你能够给我点个赞,鼓励一下我。感谢感谢……
参考资料:
【尼姆游戏(学霸就是这样欺负人的)】https://www.bilibili.com/video/BV1ek4y1q7JD?vd_source=564abed1c36a31978eb9de7cdc6668d2
博客原文链接:https://blog.csdn.net/Wu_L7/article/details/126266519
同时感谢上面两位创作者的输出,让我受益匪浅。
相关文章:

Nim游戏:取石头
(一)一堆取石头 背景: 在博弈论中,有一种称为Nim游戏的经典问题,它涉及到取石子的问题,其中有许多变种。Nim游戏是一种零和博弈,即两名玩家交替行动,每次只能从一堆物品中取走一定数…...
springboot国际化
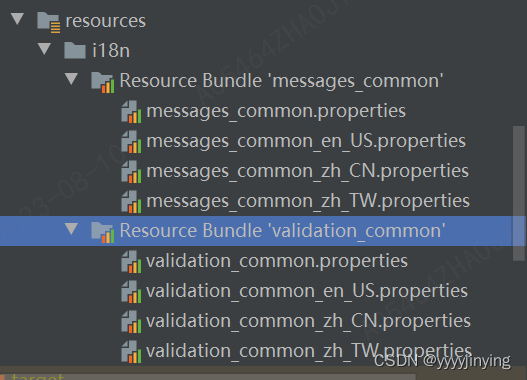
springboot国际化 不需要引入额外的jar包 参考:https://zhuanlan.zhihu.com/p/551605839 1.rources要创建Resource Bundle 2.yml配置中引入Resource Bundle 引入Resource Bundle spring:messages:encoding: UTF-8basename: i18n/messages_common3.创建国际化工具…...

12种不宜使用的Javascript语法
1. Javascript有两组相等运算符,一组是和!,另一组是和!。前者只比较值的相等,后者除了值以外,还比较类型是否相同。 请尽量不要使用前一组,永远只使用和!。因为默认会进行类型转换,规则十分难记。如果你…...

vue3+element-plus点击列表中的图片预览时,图片被表格覆盖
文章目录 问题解决 问题 视觉 点击图片进行预览,但还能继续选中其他的图片进行预览,鼠标放在表格上,那一行表格也会选中,如图所示第一行的效果。 代码 <el-table-column prop"id" label"ID" width"…...

flutter:二维码生成与读取
前言 这csdn真的是服了,图片里有个二维码就直接变成违规图片了。至于效果的话,自己运行一下看看吧。 生成 flutter中生成二维码可以使用 qr_flutter。 官方文档 https://pub-web.flutter-io.cn/packages/qr_flutter 安装 flutter pub add qr_flutt…...

Camunda 7.x 系列【14】核心概念
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 2.7.9 本系列Camunda 版本 7.19.0 源码地址:https://gitee.com/pearl-organization/camunda-study-demo 文章目录 1. 流程定义1.1 Key1.2 版本1.3 挂起2. 流程实例3. 执行4. 活动实例5. 作业和作业定义本篇文…...
matplotlib 笔记:hist2d 2D直方图
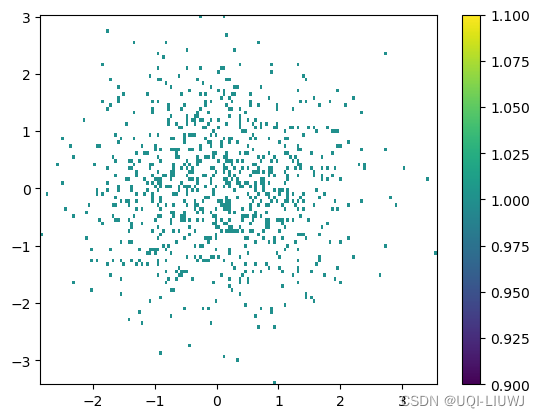
创建二维直方图,用于显示数据分布的图表将数据划分成不同的区间(bin),并统计每个区间内数据点的数量 1 基本画法 默认bin的数量是10*10 N 1000 x np.random.randn(N) y np.random.randn(N) plt.hist2d(x, y) 2 修改bin的…...

数据库优化脚本执行报错
目录 一、执行数据库优化脚本 报错... 3 解决方法:... 4 1、直接注释掉RECYCLE_POOLS 赋值sql语句块... 4 2、手动修改脚本... 5 附录... 6 一、执行数据库优化脚本 报错 AutoParaAdj3.5_dm8.sql 1)manager中报错 -20001: 执行失败, -7065 数据未…...

TopN漏洞--sql注入
sql注入 SQL注入即是指web应用程序对用户输入数据的合法性没有判断或过滤不严,攻击者可以在web应用程序中事先定义好的查询语句的结尾上添加额外的SQL语句,在管理员不知情的情况下实现非法操作,以此来实现欺骗数据库服务器执行非授权的任意查…...

【论文阅读】UNICORN:基于运行时来源的高级持续威胁检测器(NDSS-2020)
UNICORN: Runtime Provenance-Based Detector for Advanced Persistent Threats NDSS-2020 哈佛大学 Han X, Pasquier T, Bates A, et al. Unicorn: Runtime provenance-based detector for advanced persistent threats[J]. arXiv preprint arXiv:2001.01525, 2020. 源码&…...

Linux的基本介绍和常用命令
Linux和Windows的主要区别 Linux和Windows是两种具有不同特性的操作系统,它们具有各自的优点和适用场景。选择哪一个操作系统主要取决于用户的需求、技术背景及使用场景等。 Linux和Windows的主要区别如下: 开源VS闭源:Linux是开源的系统&…...

Flutter 中
在Get状态管理库中,GetxController是一个用于管理状态和逻辑的基类。它具有一系列的生命周期方法,用于在不同的阶段执行相关的操作。下面是GetxController的生命周期方法及其执行顺序: onInit(): 这个方法在GetxController创建并加入到管理器…...

可视化高级绘图技巧100篇-总论
前言 优秀的数据可视化作品可以用三个关键词概括:准确、清晰、优雅。 准确:精准地反馈数据的特征信息(既不遗漏也不冗余,不造成读者疏漏&误读细节) 清晰:获取图表特征信息的时间越短越好 优雅&…...

Android AOSP源码编译——AOSP下载(一)
一、电脑配置 Ubuntu16.04 16G,硬盘的大小最好大于300G (我这边是找了个win电脑装了双系统 没有使用虚拟机的方式) 二、基础环境配置 1、安装git sudo apt install git配置git email和name git config --global user.email "youexample.com" git conf…...
Qt 文件对话框使用 Deepin风格
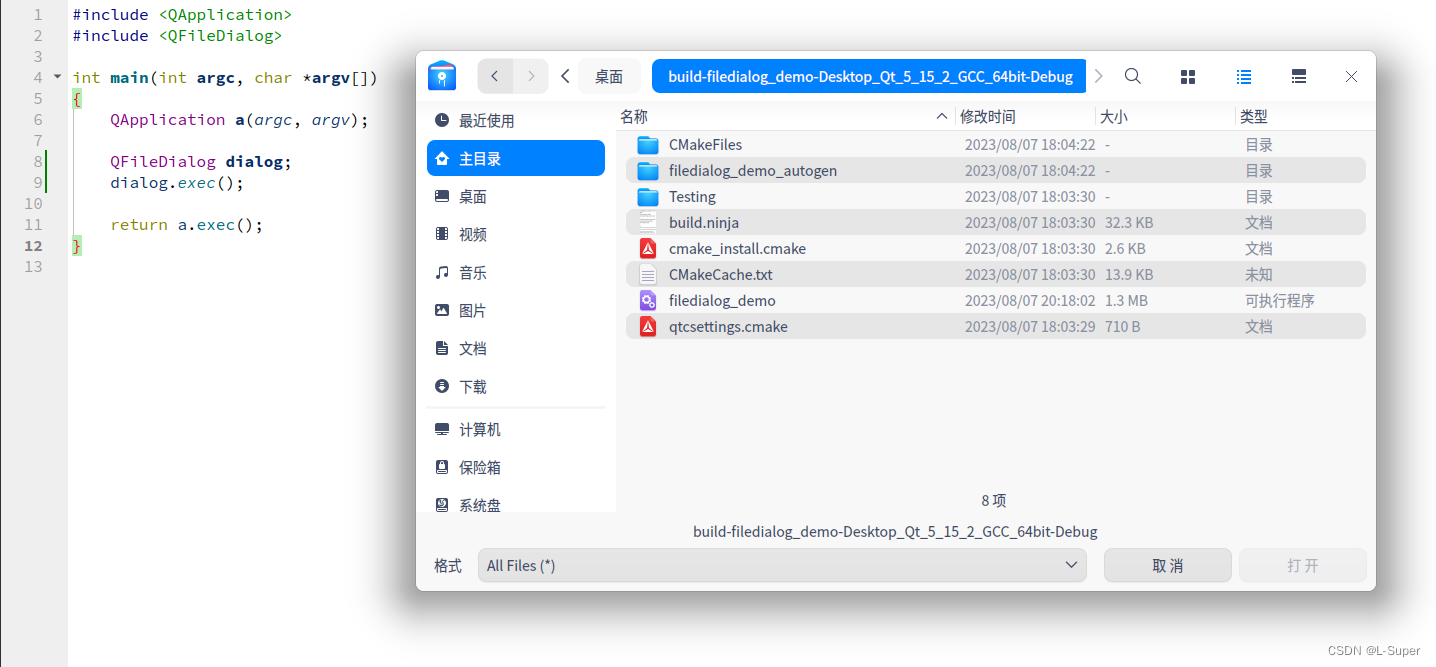
当你在Deepin或UOS 上开发 Qt 程序时,如果涉及到文件对话框功能,那么就会遇到调用原生窗口的问题。 如果你使用的是官方的Qt版本,那么在Deepin或者UOS系统上,弹出的文件对话框会是如下这样: 而Deepin或UOS系统提供的默…...

.net core 配置swagger
要在 ASP.NET Core 中配置 Swagger,您需要遵循以下步骤: 添加 Swagger NuGet 包:将 Swashbuckle.AspNetCore NuGet 包添加到项目中。 在 Startup.cs 文件中进行配置: using Microsoft.OpenApi.Models;public class Startup {// 省…...
)
leetcode707. 设计链表(单链表+虚拟头指针+双指针遍历)
题目:leetcode707. 设计链表 描述: 你可以选择使用单链表或者双链表,设计并实现自己的链表。 单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。 如果是双向链…...
电脑麦克风没声音?
这3招就可以解决! 在我们使用电脑录制视频时,有时会遇到一个令人头疼的问题:麦克风没有声音。那么,为什么会出现这种情况呢?更重要的是,我们应该如何解决这个问题呢?本文将介绍3种方法…...
React Native元素旋转一定的角度
mMeArrowIcon: {fontSize: 30, color: #999, transform: [{rotate: 180deg}]},<Icon name"arrow" style{styles.mMeArrowIcon}></Icon>参考链接: https://reactnative.cn/docs/transforms https://chat.xutongbao.top/...

LeetCode 1749. 任意子数组和的绝对值的最大值
【LetMeFly】1749.任意子数组和的绝对值的最大值 力扣题目链接:https://leetcode.cn/problems/maximum-absolute-sum-of-any-subarray/ 给你一个整数数组 nums 。一个子数组 [numsl, numsl1, ..., numsr-1, numsr] 的 和的绝对值 为 abs(numsl numsl1 ... nums…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...

Qt Quick Controls模块功能及架构
Qt Quick Controls是Qt Quick的一个附加模块,提供了一套用于构建完整用户界面的UI控件。在Qt 6.0中,这个模块经历了重大重构和改进。 一、主要功能和特点 1. 架构重构 完全重写了底层架构,与Qt Quick更紧密集成 移除了对Qt Widgets的依赖&…...
