一元三次方程求解
一元三次方程求解
- 题目描述
- 提示
- 输入输出格式
- 输入格式
- 输出格式
- 输入输出样例
- 输入样例
- 输出样例
- 算法分析
- A C 代码
题目描述
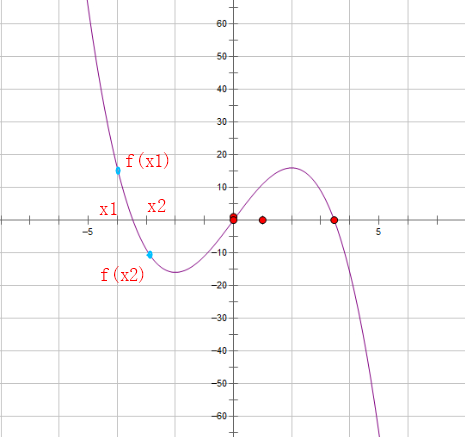
有形如: a x 3 + b x 2 + c x + d = 0 ax^3+bx^2+c^x+d=0 ax3+bx2+cx+d=0一元三次方程。给出该方程中各项的系数 ( a a a, b b b, c c c, d d d 均为实数 ),并约定该方程存在三个不同实根 (根的范围在 − 100 -100 −100至 100 100 100之间 ),且根与根之差的绝对值 ≤ 1 ≤1 ≤1。要求由小到大依次在同一行上输出这三个实根。
提示
记方程 f ( x ) = 0 f(x)=0 f(x)=0,若存在两个数 x 1 x_1 x1和 x 2 x_2 x2,且 x 1 < x 2 x_1 < x_2 x1<x2, f ( x 1 ) × f ( x 2 ) < 0 f(x_1)×f(x_2)<0 f(x1)×f(x2)<0,则在 ( x 1 , x 2 ) (x_1,x_2) (x1,x2)之间一定有一个根。
输入输出格式
输入格式
输入 a , b , c , d a,b,c,d a,b,c,d
输出格式
三个实根(根与根之间留有空格)
输入输出样例
输入样例
1 -5 -4 20
输出样例
-2.00 2.00 5.00
算法分析
这是一道有趣的解方程题。为了便于求解,设方程 f ( x ) = a x 3 + b x 2 + c x + d = 0 f(x)=ax^3+bx^2+cx+d=0 f(x)=ax3+bx2+cx+d=0,设根的值域( − 100 -100 −100至 100 100 100之间)中有 x x x, 其左右两边相距 0.0005 0.0005 0.0005的地方有 x 1 x_1 x1和 x 2 x_2 x2两个数,即 x 1 = x − 0.0005 x_1=x-0.0005 x1=x−0.0005, x 2 = x + 0.0005 x_2=x+0.0005 x2=x+0.0005。 x 1 x_1 x1和 x 2 x_2 x2间的距离( 0.001 0.001 0.001)满足精度要求(精确到小数点后 2 2 2位)。
A C 代码
暴力出奇迹~~
#include <bits/stdc++.h>
using namespace std;
double a,b,c,d;
int main()
{cin >>a >>b >>c >>d;for(double i=-100;i<=100;i+=0.001){double j=i+0.001;double l=a*i*i*i+b*i*i+c*i+d;double r=a*j*j*j+b*j*j+c*j+d;if(l*r<=0){printf("%.2lf ",(i+j)/2);}}return 0;
}
相关文章:

一元三次方程求解
一元三次方程求解 题目描述提示输入输出格式输入格式输出格式 输入输出样例输入样例输出样例 算法分析A C 代码 题目描述 有形如: a x 3 b x 2 c x d 0 ax^3bx^2c^xd0 ax3bx2cxd0一元三次方程。给出该方程中各项的系数 ( a a a, b b b,…...

基于java在线音乐网站设计与实现
在线音乐网站的设计与实现 摘 要 随着互联网趋势的到来,各行各业都在考虑利用互联网将自己推广出去,最好方式就是建立自己的互联网系统,并对其进行维护和管理。在现实运用中,应用软件的工作规则和开发步骤,采用SSM框架…...

Python爬虫如何更换ip防封
作为一名长期扎根在爬虫行业动态ip解决方案的技术员,我发现很多人常常在使用Python爬虫时遇到一个困扰,那就是如何更换IP地址。别担心,今天我就来教你如何在Python爬虫中更换IP,让你的爬虫不再受到IP封锁的困扰。废话不多说&#…...

涛思数据联合长虹佳华、阿里云 Marketplace 正式发布 TDengine Cloud
近日,涛思数据联合长虹佳华,正式在阿里云 Marketplace 发布全托管的时序数据云平台 TDengine Cloud,为用户提供更加丰富的订购渠道。目前用户可通过阿里云 Marketplace 轻松实现 TDengine Cloud 的订阅与部署,以最低的成本搭建最高…...
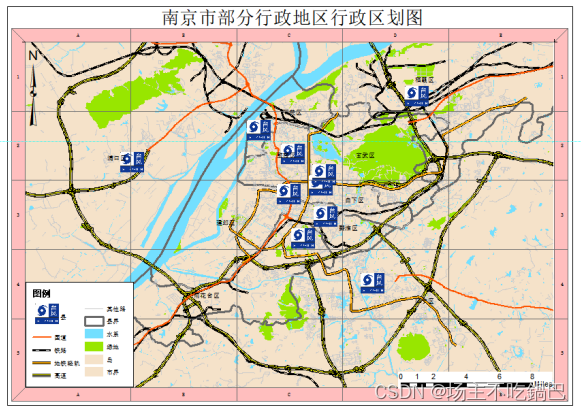
特殊符号的制作 台风 示例 使用第三方工具 Photoshop 地理信息系统空间分析实验教程 第三版
特殊符号的制作 首先这是一个含有字符的,使用arcgis自带的符号编辑器制作比较困难。所以我们准备采用Adobe Photoshop 来进行制作符号,然后直接导入符号的图片文件作为符号 我们打开ps,根据上面的图片的像素长宽比,设定合适的高度…...
IoTDB1.X windows运行失败问题的处理
在windows运行 IoTDB1.x时 会出现如图所示的问题 为什么会出现这样的问题?java没有安装还是未调用成功,我是JAVA8~11~17各种更换都未能解决问题,最后对其bat文件进行查看,发现在conf\datanode-env.bat、conf\confignode-env.bat这…...

pdf转图片【java版实现】
一、引入依赖 引入需要导入到项目中的依赖,如下所示: <!-- pdf转图片 --><dependency><groupId>net.sf.cssbox</groupId><artifactId>pdf2dom</artifactId><version>1.7</version></dependency>…...

python3.6 安装pillow失败
问题描述 python3 安装 pillow 失败 错误原因 python3.6 不支持 pillow9.0 以上的版本 解决方法: 指定版本安装 e.g., pillow8.0 pip3 install pillow8.0...

巨人互动|Meta海外户Meta的业务工具转化API
Meta的业务工具转化API是一项创新技术,它可以帮助企业实现更高效的业务工具转化和集成。通过这个API,企业可以将不同的业务工具整合到一个统一的平台上,提高工作效率和协作能力。本文小编将介绍Meta的业务工具转化API的功能和优势。 巨人互动…...

【JAVA】包、权限修饰符、final关键字、常量、枚举、抽象类、接口
1 包 包是用来分门别类的管理各种不同类的,类似于文件夹、建包利于程序的管理和维护。建包语句必须在第一行建包的语法格式:package 公司域名倒写.项目名称。包名建议全部小写相同包下的类可以直接访问,不同包下的类必须导包,才可…...
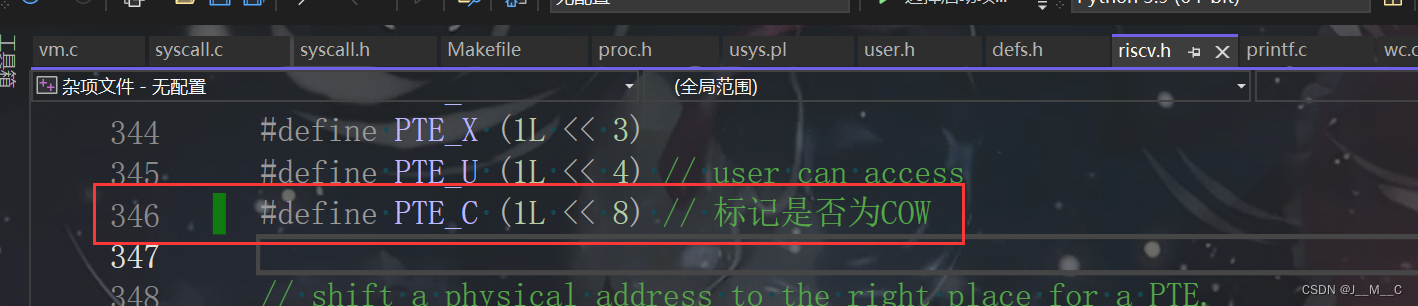
6.s081/6.1810(Fall 2022)Lab5: Copy-on-Write Fork for xv6
前言 本来往年这里还有个Lazy Allocation的,今年不知道为啥直接给跳过去了。. 其他篇章 环境搭建 Lab1: Utilities Lab2: System calls Lab3: Page tables Lab4: Traps Lab5: Copy-on-Write Fork for xv6 参考链接 官网链接 xv6手册链接,这个挺重要…...
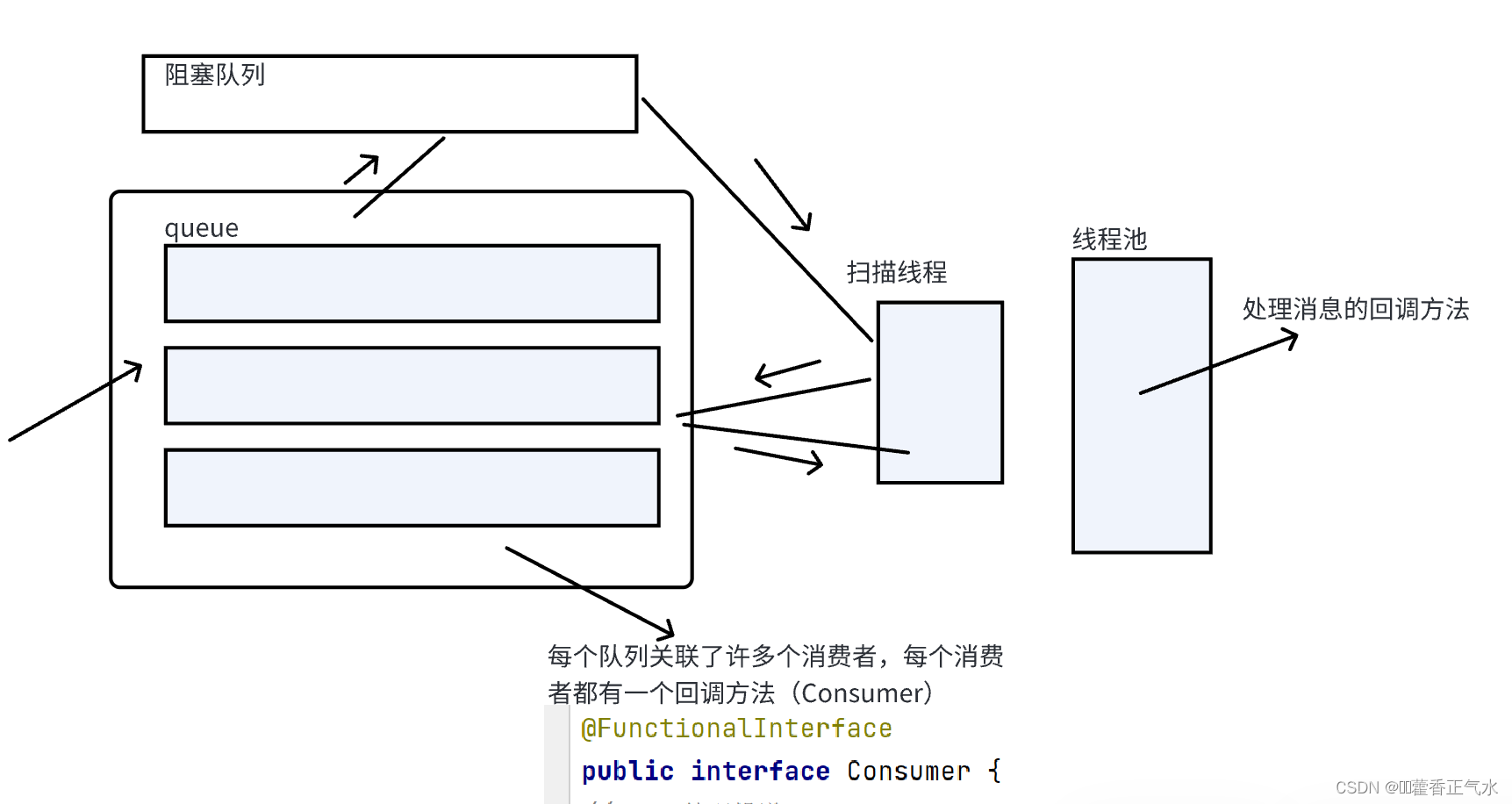
项目实战 — 消息队列(7){虚拟主机设计(2)}
目录 一、消费消息的规则 二、消费消息的具体实现方法 🍅 1、编写消费者类(ConsumerEnv) 🍅 2、编写Consumer函数式接口(回调函数) 🍅 3、编写ConsumeerManager类 🎄定义成员变…...
手把手教你快速实现内网穿透
快速内网穿透教程 文章目录 快速内网穿透教程前言*cpolar内网穿透使用教程*1. 安装cpolar内网穿透工具1.1 Windows系统1.2 Linux系统1.2.1 安装1.2.2 向系统添加服务1.2.3 启动服务1.2.4 查看服务状态 2. 创建隧道映射内网端口3. 获取公网地址 前言 要想实现在公网访问到本地的…...

【Linux取经路】揭秘进程的父与子
文章目录 1、进程PID1.1 通过系统调用接口查看进程PID1.2 父进程与子进程 2、通过系统调用创建进程-fork初始2.1 调用fork函数后的现象2.2 为什么fork给子进程返回0,给父进程返回pid?2.3 fork函数是如何做到返回两次的?2.4 一个变量怎么会有不…...

iOS链式编程风格 -- 富文本字符串
一、概念 链式编程风格是一种将多个函数调用连接起来,形成一条函数调用链的编程风格。这种风格的代码可以通过返回 self 或某个适当的对象来实现。 1.优点 代码简洁、连贯、易于阅读。可以将一个方法的输出直接作为下一个方法的输入,降低中间变量的使…...

后端开发5.Redis的搭建
使用docker安装 Redis【redis】(6379) 拉取Redis镜像 docker pull redis:6.2.6 启动Redis容器 docker run -di --name=redis -p 6379:6379 redis:6.2.6 启动Redis容器并设置密码 docker run -di --name=redis -p 6379:6379 redis:6.2.6 --requirepass "密码" 测…...

推特群推王构建你的流量池
随着社交媒体的兴起,推特已成为了一个信息传播、交流、互动的重要平台。在这个充满了各种声音和观点的数字世界里,如何有效地将自己的声音传达出去,吸引更多的关注和互动,已经成为了一个备受关注的话题。而在这个过程中࿰…...
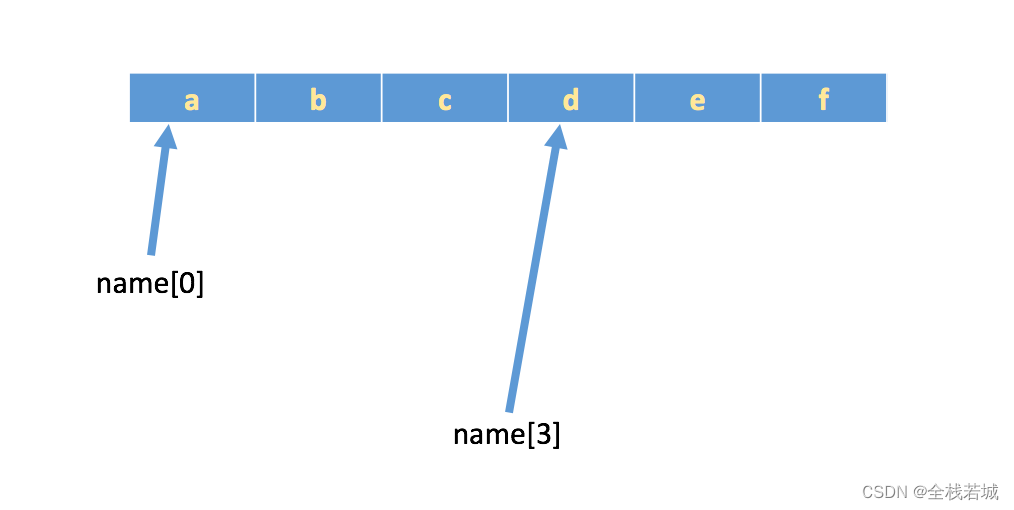
【从零学习python 】12.Python字符串操作与应用
文章目录 学习目标字符串介绍字符串表示方式小总结转义字符 下标和切片一、 下标/索引1. 如果想取出部分字符,那么可以通过下标的方法,(注意在计算机中,下标从 0 开始)2. 遍历3. 切片 进阶案例 学习目标 字符串的表示…...

MongoDB创建用户 、数据库、索引等基础操作
MongoDB的权限认证是相对来说比较复杂的,不同的库创建后需要创建用户来管理。 本机中的MongoDB是docker 启动的,所以先进入docker的镜像中 docker exec -it mongodb bash 这样就进入到了镜像MongoDB中,然后输入命令连接MongoDB数据库 注…...
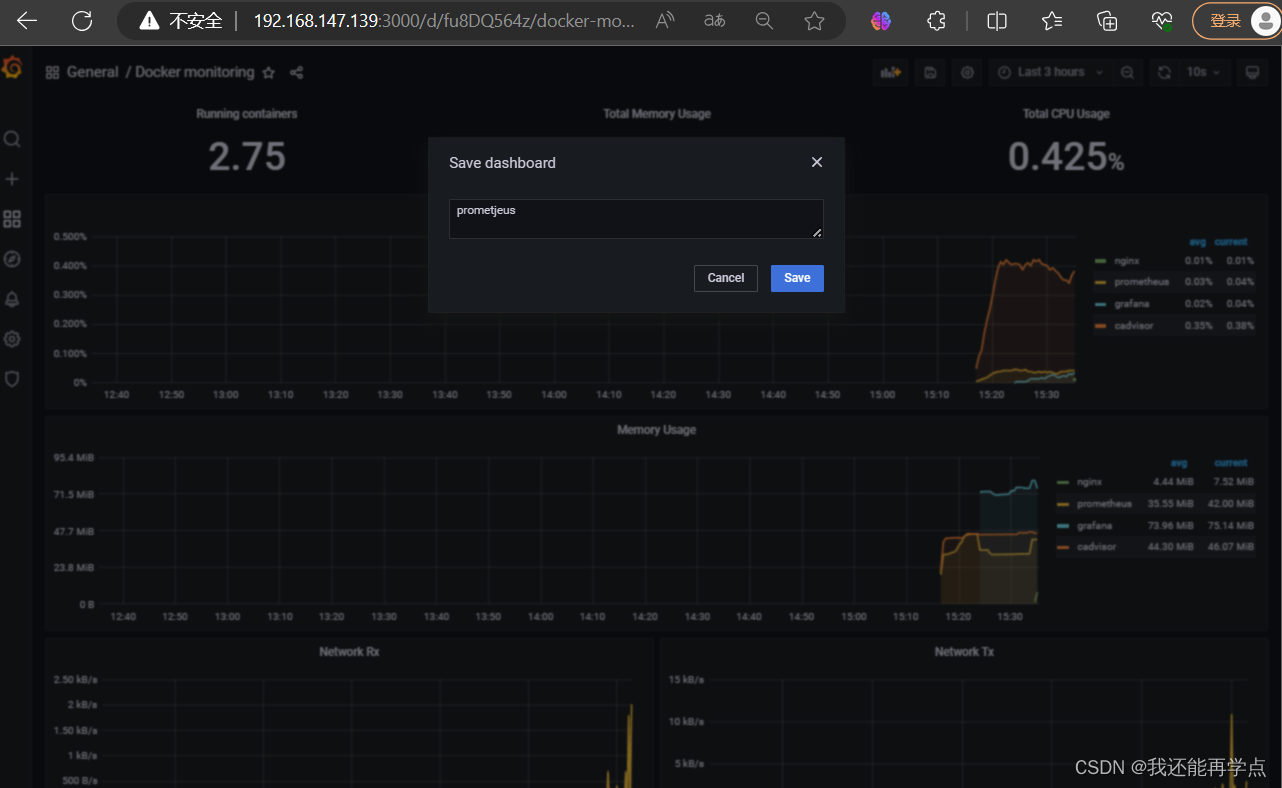
Docker容器监控(Cadvisor +Prometheus+Grafana)
环境部署,接着上一篇文章Docker容器部署(Cadvisor InfluxDBGrafana)开始 目录 1、先清理一下容器 2、部署Cadvisor 3、访问Cadvisor页面 4、部署Prometheus 5、准备配置 6、运行prometheus容器 7、访问prometheus页面 8、部署Grafan…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
