28 玻尔兹曼机
文章目录
- 28 玻尔兹曼机
- 28.1 模型定义
- 28.2 梯度推导
- 28.3 梯度上升
- 28.4 基于VI[平均场理论]求解后验概率
28 玻尔兹曼机
28.1 模型定义
玻尔兹曼机是一张无向图,其中的隐节点和观测节点可以有任意连接如下图:
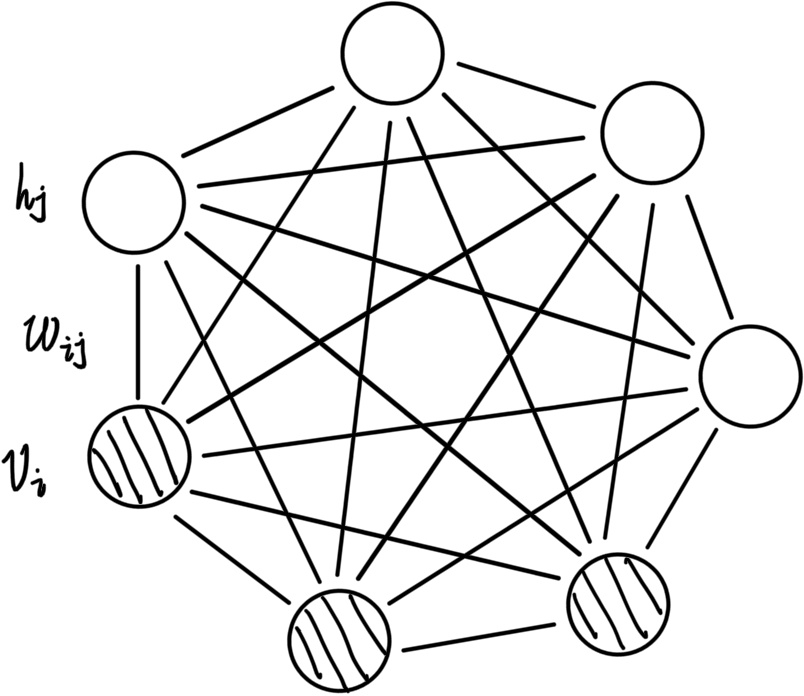
我们给其中的节点、连线做出一些定义:
- 节点:观测节点 V = { 0 , 1 } D V = {\lbrace 0, 1 \rbrace}^D V={0,1}D,隐节点 H = { 0 , 1 } P H = {\lbrace 0, 1 \rbrace}^P H={0,1}P
- 连线:观测节点之间 L = [ L i j ] D × D L = [L_{ij}]_{D \times D} L=[Lij]D×D,隐节点之间 J = [ J i j ] P × P J = [J_{ij}]_{P \times P} J=[Jij]P×P,观测节点与隐节点之间 W = [ W i j ] D × P W = [W_{ij}]_{D \times P} W=[Wij]D×P
- 参数: θ = { W , L , J } \theta = {\lbrace W, L, J \rbrace} θ={W,L,J}
则我们可以根据上面的定义,加上无向图能量方程的性质得到公式:
{ P ( V ∣ H ) = 1 z e x p − E ( V , H ) E ( V , H ) = − ( V T W H + 1 2 V T L V + 1 2 H T J H ⏟ 矩阵对称,参数除 2 ) \begin{cases} P(V|H) = \frac{1}{z} exp{-E(V, H)} \\ E(V, H) = -( {V^T W H} + \underbrace{\frac{1}{2} {V^T L V} + \frac{1}{2} {H^T J H}}_{矩阵对称,参数除2} ) \end{cases} ⎩ ⎨ ⎧P(V∣H)=z1exp−E(V,H)E(V,H)=−(VTWH+矩阵对称,参数除2 21VTLV+21HTJH)
28.2 梯度推导
我们的目标函数就是 P ( V ) P(V) P(V),所以可以讲log-likelihood写作: 1 N ∑ v ∈ V log P ( v ) \frac{1}{N} \sum_{v \in V} \log P(v) N1∑v∈VlogP(v),并且 ∣ V ∣ = N |V| = N ∣V∣=N。所以我们可以将他的梯度写为 1 N ∑ v ∈ V ∇ θ log P ( v ) \frac{1}{N} \sum_{v \in V} \nabla_\theta \log P(v) N1∑v∈V∇θlogP(v)。其中 ∇ θ log P ( v ) \nabla_\theta \log P(v) ∇θlogP(v)的推导在24-直面配分函数的RBM-Learning问题中已经推导过了,可以得到:
∇ θ log P ( v ) = ∑ v ∑ H P ( v , H ) ⋅ ∇ θ E ( v , H ) − ∑ H P ( H ∣ v ) ⋅ ∇ θ E ( v , H ) \nabla_\theta \log P(v) = \sum_v \sum_H P(v, H) \cdot \nabla_\theta E(v, H) - \sum_H P(H| v) \cdot \nabla_\theta E(v, H) ∇θlogP(v)=v∑H∑P(v,H)⋅∇θE(v,H)−H∑P(H∣v)⋅∇θE(v,H)
我们对E(v, H)求其中一个参数的导的结果很容易求,所以可以将公式写作:
∇ w log P ( v ) = ∑ v ∑ H P ( v , H ) ⋅ ( − V H T ) − ∑ H P ( H ∣ v ) ⋅ ( − V H T ) = ∑ H P ( H ∣ v ) ⋅ V H T − ∑ v ∑ H P ( v , H ) ⋅ V H T \begin{align} \nabla_w \log P(v) &= \sum_v \sum_H P(v, H) \cdot (- V H^T) - \sum_H P(H| v) \cdot (- V H^T) \\ &= \sum_H P(H| v) \cdot V H^T - \sum_v \sum_H P(v, H) \cdot V H^T \end{align} ∇wlogP(v)=v∑H∑P(v,H)⋅(−VHT)−H∑P(H∣v)⋅(−VHT)=H∑P(H∣v)⋅VHT−v∑H∑P(v,H)⋅VHT
将其带入原式可得:
∇ w L = 1 N ∑ v ∈ V ∇ θ log P ( v ) = 1 N ∑ v ∈ V ∑ H P ( H ∣ v ) ⋅ V H T − 1 N ∑ v ∈ V ⏟ 1 N × N ∑ v ∑ H P ( v , H ) ⋅ V H T = 1 N ∑ v ∈ V ∑ H P ( H ∣ v ) ⋅ V H T − ∑ v ∑ H P ( v , H ) ⋅ V H T \begin{align} \nabla_w {\mathcal L} &= \frac{1}{N} \sum_{v \in V} \nabla_\theta \log P(v) \\ &= \frac{1}{N} \sum_{v \in V} \sum_H P(H| v) \cdot V H^T - \underbrace{\frac{1}{N} \sum_{v \in V}}_{\frac{1}{N} \times N} \sum_v \sum_H P(v, H) \cdot V H^T \\ &= \frac{1}{N} \sum_{v \in V} \sum_H P(H| v) \cdot V H^T - \sum_v \sum_H P(v, H) \cdot V H^T \\ \end{align} ∇wL=N1v∈V∑∇θlogP(v)=N1v∈V∑H∑P(H∣v)⋅VHT−N1×N N1v∈V∑v∑H∑P(v,H)⋅VHT=N1v∈V∑H∑P(H∣v)⋅VHT−v∑H∑P(v,H)⋅VHT
我们用 P d a t a P_{data} Pdata表示 P d a t a ( v , H ) = P d a t a ( v ) ⋅ P m o d e l ( H ∣ v ) P_{data}(v, H) = P_{data}(v) \cdot P_{model}(H| v) Pdata(v,H)=Pdata(v)⋅Pmodel(H∣v), P m o d e l P_{model} Pmodel表示 P m o d e l ( v , H ) P_{model}(v, H) Pmodel(v,H),则可以将公式再转化为:
∇ w L = E P d a t a [ V H T ] − E P m o d e l [ V H T ] \begin{align} \nabla_w {\mathcal L} &= E_{P_{data}} \left[ V H^T \right] - E_{P_{model}} \left[ V H^T \right] \end{align} ∇wL=EPdata[VHT]−EPmodel[VHT]
28.3 梯度上升
给三个参数分别写出他们的变化量(系数 × \times ×梯度):
{ Δ W = α ( E P d a t a [ V H T ] − E P m o d e l [ V H T ] ) Δ L = α ( E P d a t a [ V V T ] − E P m o d e l [ V V T ] ) Δ J = α ( E P d a t a [ H H T ] − E P m o d e l [ H H T ] ) \begin{cases} \Delta W = \alpha (E_{P_{data}} \left[ V H^T \right] - E_{P_{model}} \left[ V H^T \right]) \\ \Delta L = \alpha (E_{P_{data}} \left[ V V^T \right] - E_{P_{model}} \left[ V V^T \right]) \\ \Delta J = \alpha (E_{P_{data}} \left[ H H^T \right] - E_{P_{model}} \left[ H H^T \right]) \\ \end{cases} ⎩ ⎨ ⎧ΔW=α(EPdata[VHT]−EPmodel[VHT])ΔL=α(EPdata[VVT]−EPmodel[VVT])ΔJ=α(EPdata[HHT]−EPmodel[HHT])
这是用于表示在一次梯度上升中参数的改变量,由于 W , L , J W,L,J W,L,J是矩阵,将他们拆的更细可以写作:
Δ w i j = α ( E P d a t a [ v i h j ] ⏟ positive phase − E P m o d e l [ v i h j ] ⏟ negative phase ) \Delta w_{ij} = \alpha ( \underbrace{E_{P_{data}} \left[ v_i h_j \right]}_{\text{positive phase}} - \underbrace{E_{P_{model}} \left[ v_i h_j \right]}_{\text{negative phase}} ) Δwij=α(positive phase EPdata[vihj]−negative phase EPmodel[vihj])
但是这两项都很难求,因为要用到 P m o d e l P_{model} Pmodel,如果要得到 P m o d e l P_{model} Pmodel则要采用MCMC的方法,但对一个这样的图进行MCMC非常的消耗时间(不过这也给我们提供了一个解题思路)。
具体要用到MCMC的话,我们必须要有每一个维度的后验,所以我们根据复杂的推导(下面证明)可以得到每一个维度的后验——在固定其他维度求这一个维度的情况:
{ P ( v i = 1 ∣ H , V − i ) = σ ( ∑ j = 1 P w i j h j + ∑ k = 1 , − i D L i k v k ) P ( h j = 1 ∣ V , H − j ) = σ ( ∑ i = 1 P w i j v i + ∑ m = 1 , − i D J j m h m ) \begin{cases} P(v_i = 1|H, V_{-i}) = \sigma(\sum_{j=1}^P w_{ij} h_j + \sum_{k=1,-i}^D L_{ik} v_k) \\ P(h_j = 1|V, H_{-j}) = \sigma(\sum_{i=1}^P w_{ij} v_i + \sum_{m=1,-i}^D J_{jm} h_m) \\ \end{cases} {P(vi=1∣H,V−i)=σ(∑j=1Pwijhj+∑k=1,−iDLikvk)P(hj=1∣V,H−j)=σ(∑i=1Pwijvi+∑m=1,−iDJjmhm)
这个公式我们可以发现在RBM情况下也是符合RBM后验公式的。
接下来我们证明一下上面这个公式,下文验证 P ( v i ∣ H , V − i ) P(v_i|H, V_{-i}) P(vi∣H,V−i)的情况, P ( h j ∣ V , H − j ) P(h_j|V, H_{-j}) P(hj∣V,H−j)可以类比。首先对其进行变换:
P ( v i ∣ H , V − i ) = P ( H , V ) P ( H , V − i ) = 1 Z exp { − E [ V , H ] } ∑ v i 1 Z exp { − E [ V , H ] } = 1 Z exp { V T W H + 1 2 V T L V + 1 2 H T J H } ∑ v i 1 Z exp { V T W H + 1 2 V T L V + 1 2 H T J H } = 1 Z exp { V T W H + 1 2 V T L V } ⋅ exp { 1 2 H T J H } 1 Z exp { 1 2 H T J H } ⋅ ∑ v i exp { V T W H + 1 2 V T L V } = exp { V T W H + 1 2 V T L V } ∑ v i exp { V T W H + 1 2 V T L V } = exp { V T W H + 1 2 V T L V } ∣ v i = 1 exp { V T W H + 1 2 V T L V } ∣ v i = 0 + exp { V T W H + 1 2 V T L V } ∣ v i = 1 \begin{align} P(v_i|H, V_{-i}) &= \frac{P(H, V)}{P(H, V_{-i})} \\ &= \frac{ \frac{1}{Z} \exp{\lbrace - E[V, H] \rbrace} }{ \sum_{v_i} \frac{1}{Z} \exp{\lbrace - E[V, H] \rbrace}} \\ &= \frac{ \frac{1}{Z} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} + \frac{1}{2} {H^T J H} \rbrace} }{ \sum_{v_i} \frac{1}{Z} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} + \frac{1}{2} {H^T J H} \rbrace}} \\ &= \frac{ \frac{1}{Z} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace} \cdot \exp{\lbrace \frac{1}{2} {H^T J H} \rbrace} }{ \frac{1}{Z} \exp{\lbrace \frac{1}{2} {H^T J H} \rbrace} \cdot \sum_{v_i} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}} \\ &= \frac{ \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace} }{ \sum_{v_i} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}} \\ &= \frac{ \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}|_{v_i = 1} }{ \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}|_{v_i = 0} + \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}|_{v_i = 1} } \\ \end{align} P(vi∣H,V−i)=P(H,V−i)P(H,V)=∑viZ1exp{−E[V,H]}Z1exp{−E[V,H]}=∑viZ1exp{VTWH+21VTLV+21HTJH}Z1exp{VTWH+21VTLV+21HTJH}=Z1exp{21HTJH}⋅∑viexp{VTWH+21VTLV}Z1exp{VTWH+21VTLV}⋅exp{21HTJH}=∑viexp{VTWH+21VTLV}exp{VTWH+21VTLV}=exp{VTWH+21VTLV}∣vi=0+exp{VTWH+21VTLV}∣vi=1exp{VTWH+21VTLV}∣vi=1
若我们将相同的部份表示为 Δ v i \Delta_{v_i} Δvi,则可以将公式写为:
P ( v i ∣ H , V − i ) = Δ v i ∣ v i = 1 Δ v i ∣ v i = 0 + Δ v i ∣ v i = 1 \begin{align} P(v_i|H, V_{-i}) &= \frac{ \Delta_{v_i}|_{v_i = 1} }{ \Delta_{v_i}|_{v_i = 0} + \Delta_{v_i}|_{v_i = 1} } \\ \end{align} P(vi∣H,V−i)=Δvi∣vi=0+Δvi∣vi=1Δvi∣vi=1
其中 Δ v i \Delta_{v_i} Δvi可以做如下变换:
Δ v i = exp { V T W H + 1 2 V T L V } = exp { ∑ i ^ = 1 D ∑ j = 1 P v i ^ W i ^ j h j + 1 2 ∑ i ^ = 1 D ∑ k = 1 D v i ^ L i ^ k v k } \begin{align} \Delta_{v_i} &= \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace} \\ &= \exp{\lbrace \sum_{{\hat i} = 1}^{D} \sum_{j = 1}^{P} {v_{\hat i} W_{{\hat i} j} h_j} + \frac{1}{2} \sum_{{\hat i} = 1}^{D} \sum_{k = 1}^{D} {v_{\hat i} L_{{\hat i} k} v_k} \rbrace} \end{align} Δvi=exp{VTWH+21VTLV}=exp{i^=1∑Dj=1∑Pvi^Wi^jhj+21i^=1∑Dk=1∑Dvi^Li^kvk}
我们接下来将有 v i v_i vi的项全部拆分出来:
Δ v i = exp { ∑ i ^ = 1 , − i D ∑ j = 1 P v i ^ W i ^ j h j + ∑ j = 1 P v i W i j h j } ⋅ exp { 1 2 ( ∑ i ^ = 1 , − i D ∑ k = 1 , − i D v i ^ W i ^ k h k + v i L i i v i ⏟ 0 + ∑ i ^ = 1 , − i D v i ^ W i ^ i v i ⏟ 相同 + ∑ k = 1 , − i D v i L i k v k ) } = exp { ∑ i ^ = 1 , − i D ∑ j = 1 P v i ^ W i ^ j h j + ∑ j = 1 P v i W i j h j + 1 2 ∑ i ^ = 1 , − i D ∑ k = 1 , − i D v i ^ W i ^ k h k + ∑ k = 1 , − i D v i L i k v k } \begin{align} \Delta_{v_i} &= \exp{\lbrace \sum_{{\hat i} = 1, -i}^{D} \sum_{j = 1}^{P} {v_{\hat i} W_{{\hat i} j} h_j} + \sum_{j = 1}^{P} {v_i W_{i j} h_j} \rbrace} \\ & \cdot \exp{\lbrace \frac{1}{2} \left( \sum_{{\hat i} = 1, -i}^{D} \sum_{k = 1,-i}^{D} {v_{\hat i} W_{{\hat i} k} h_k} + \underbrace{v_i L_{ii} v_i}_{0} + \underbrace{\sum_{{\hat i} = 1, -i}^{D} {v_{\hat i} W_{{\hat i} i} v_i}}_{相同} + \sum_{k = 1, -i}^{D} {v_i L_{i k} v_k} \right) \rbrace} \\ &= \exp{\lbrace \sum_{{\hat i} = 1, -i}^{D} \sum_{j = 1}^{P} {v_{\hat i} W_{{\hat i} j} h_j} + \sum_{j = 1}^{P} {v_i W_{i j} h_j} + \frac{1}{2} \sum_{{\hat i} = 1, -i}^{D} \sum_{k = 1,-i}^{D} {v_{\hat i} W_{{\hat i} k} h_k} + \sum_{k = 1, -i}^{D} {v_i L_{i k} v_k} \rbrace} \end{align} Δvi=exp{i^=1,−i∑Dj=1∑Pvi^Wi^jhj+j=1∑PviWijhj}⋅exp{21 i^=1,−i∑Dk=1,−i∑Dvi^Wi^khk+0 viLiivi+相同 i^=1,−i∑Dvi^Wi^ivi+k=1,−i∑DviLikvk }=exp{i^=1,−i∑Dj=1∑Pvi^Wi^jhj+j=1∑PviWijhj+21i^=1,−i∑Dk=1,−i∑Dvi^Wi^khk+k=1,−i∑DviLikvk}
所以我们将 v i = 1 v_i = 1 vi=1和 v i = 0 v_i = 0 vi=0代入该公式即可得出结果。
Δ v i = 0 = exp { ∑ i ^ = 1 , − i D ∑ j = 1 P v i ^ W i ^ j h j + 1 2 ∑ i ^ = 1 , − i D ∑ k = 1 , − i D v i ^ W i ^ k h k } = exp { A + B } Δ v i = 1 = exp { A + B + ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } \begin{align} \Delta_{v_i = 0} &= \exp{\lbrace \sum_{{\hat i} = 1, -i}^{D} \sum_{j = 1}^{P} {v_{\hat i} W_{{\hat i} j} h_j} + \frac{1}{2} \sum_{{\hat i} = 1, -i}^{D} \sum_{k = 1,-i}^{D} {v_{\hat i} W_{{\hat i} k} h_k} \rbrace} = \exp{\lbrace A + B \rbrace} \\ \Delta_{v_i = 1} &= \exp{\lbrace A + B + \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} \end{align} Δvi=0Δvi=1=exp{i^=1,−i∑Dj=1∑Pvi^Wi^jhj+21i^=1,−i∑Dk=1,−i∑Dvi^Wi^khk}=exp{A+B}=exp{A+B+j=1∑PWijhj+k=1,−i∑DLikvk}
P ( v i ∣ H , V − i ) = Δ v i ∣ v i = 1 Δ v i ∣ v i = 0 + Δ v i ∣ v i = 1 = exp { A + B + ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } exp { A + B } + exp { A + B + ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } = exp { ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } 1 + exp { ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } = σ ( ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k ) \begin{align} P(v_i|H, V_{-i}) &= \frac{ \Delta_{v_i}|_{v_i = 1} }{ \Delta_{v_i}|_{v_i = 0} + \Delta_{v_i}|_{v_i = 1} } \\ &= \frac{ \exp{\lbrace A + B + \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} }{ \exp{\lbrace A + B \rbrace} + \exp{\lbrace A + B + \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} } \\ &= \frac{ \exp{\lbrace \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} }{ 1 + \exp{\lbrace \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} } \\ &= \sigma(\sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k}) \end{align} P(vi∣H,V−i)=Δvi∣vi=0+Δvi∣vi=1Δvi∣vi=1=exp{A+B}+exp{A+B+∑j=1PWijhj+∑k=1,−iDLikvk}exp{A+B+∑j=1PWijhj+∑k=1,−iDLikvk}=1+exp{∑j=1PWijhj+∑k=1,−iDLikvk}exp{∑j=1PWijhj+∑k=1,−iDLikvk}=σ(j=1∑PWijhj+k=1,−i∑DLikvk)
28.4 基于VI[平均场理论]求解后验概率
我们的参数,通过梯度求出的变化量可以表示为:
{ Δ W = α ( E P d a t a [ V H T ] − E P m o d e l [ V H T ] ) Δ L = α ( E P d a t a [ V V T ] − E P m o d e l [ V V T ] ) Δ J = α ( E P d a t a [ H H T ] − E P m o d e l [ H H T ] ) \begin{cases} \Delta W = \alpha (E_{P_{data}} \left[ V H^T \right] - E_{P_{model}} \left[ V H^T \right]) \\ \Delta L = \alpha (E_{P_{data}} \left[ V V^T \right] - E_{P_{model}} \left[ V V^T \right]) \\ \Delta J = \alpha (E_{P_{data}} \left[ H H^T \right] - E_{P_{model}} \left[ H H^T \right]) \\ \end{cases} ⎩ ⎨ ⎧ΔW=α(EPdata[VHT]−EPmodel[VHT])ΔL=α(EPdata[VVT]−EPmodel[VVT])ΔJ=α(EPdata[HHT]−EPmodel[HHT])
但是如果要直接求出其后验概率,还应该从 L = E L B O {\mathcal L} = ELBO L=ELBO开始分析,通过平均场理论(在VI中使用过)进行分解:
L = E L B O = log P θ ( V ) − K L ( q ϕ ∥ p θ ) = ∑ h q ϕ ( H ∣ V ) ⋅ log P θ ( V , H ) + H [ q ] \begin{align} {\mathcal L} &= ELBO = \log P_\theta(V) - KL(q_\phi \Vert p_\theta) = \sum_h q_\phi(H|V) \cdot \log P_\theta(V,H) + H[q] \end{align} L=ELBO=logPθ(V)−KL(qϕ∥pθ)=h∑qϕ(H∣V)⋅logPθ(V,H)+H[q]
我们在这里做出一些假设(将 q ( H ∣ V ) q(H|V) q(H∣V)拆分为P个维度之积):
{ q ϕ ( H ∣ V ) = ∏ j = 1 P q ϕ ( H j ∣ V ) q ϕ ( H j = 1 ∣ V ) = ϕ j ϕ = { ϕ j } j = 1 P \begin{cases} q_\phi(H|V) = \prod_{j=1}^{P} q_\phi(H_j|V) \\ q_\phi(H_j = 1| V) = \phi_j \\ \phi = \{\phi_j\}_{j=1}^P \\ \end{cases} ⎩ ⎨ ⎧qϕ(H∣V)=∏j=1Pqϕ(Hj∣V)qϕ(Hj=1∣V)=ϕjϕ={ϕj}j=1P
如果我们要求出后验概率就是学习参数 θ \theta θ,在之类也等同于学习参数 ϕ \phi ϕ,于是我们可以对 a r g max ϕ j L arg\max_{\phi_j}{\mathcal L} argmaxϕjL进行求解,我们将其进行化简:
ϕ j ^ = a r g max ϕ j L = a r g max ϕ j E L B O = a r g max ϕ j ∑ h q ϕ ( H ∣ V ) ⋅ log P θ ( V , H ) + H [ q ] = a r g max ϕ j ∑ h q ϕ ( H ∣ V ) ⋅ [ − log Z + V T W H + 1 2 V T L V + 1 2 H T J H ] + H [ q ] = a r g max ϕ j ∑ h q ϕ ( H ∣ V ) ⏟ = 1 ⋅ [ − log Z + 1 2 V T L V ] ⏟ 与h和 ϕ j 都无关,为常数C + ∑ h q ϕ ( H ∣ V ) ⋅ [ V T W H + 1 2 H T J H ] + H [ q ] = a r g max ϕ j ∑ h q ϕ ( H ∣ V ) ⋅ [ V T W H + 1 2 H T J H ] + H [ q ] = a r g max ϕ j ∑ h q ϕ ( H ∣ V ) ⋅ V T W H ⏟ ( 1 ) + 1 2 ∑ h q ϕ ( H ∣ V ) ⋅ H T J H ⏟ ( 2 ) + H [ q ] ⏟ ( 3 ) \begin{align} {\hat {\phi_j}} &= arg\max_{\phi_j} {\mathcal L} = arg\max_{\phi_j} ELBO \\ &= arg\max_{\phi_j} \sum_h q_\phi(H|V) \cdot \log P_\theta(V,H) + H[q] \\ &= arg\max_{\phi_j} \sum_h q_\phi(H|V) \cdot \left[ -\log Z + {V^T W H} + \frac{1}{2} {V^T L V} + \frac{1}{2} {H^T J H} \right] + H[q] \\ &= arg\max_{\phi_j} \underbrace{\sum_h q_\phi(H|V)}_{=1} \cdot \underbrace{\left[ -\log Z + \frac{1}{2} {V^T L V} \right]}_{\text{与h和$\phi_j$都无关,为常数C}} + \sum_h q_\phi(H|V) \cdot \left[ {V^T W H} + \frac{1}{2} {H^T J H} \right] + H[q] \\ &= arg\max_{\phi_j} \sum_h q_\phi(H|V) \cdot \left[ {V^T W H} + \frac{1}{2} {H^T J H} \right] + H[q] \\ &= arg\max_{\phi_j} \underbrace{\sum_h q_\phi(H|V) \cdot {V^T W H}}_{(1)} + \underbrace{\frac{1}{2} \sum_h q_\phi(H|V) \cdot {H^T J H}}_{(2)} + \underbrace{H[q]}_{(3)} \\ \end{align} ϕj^=argϕjmaxL=argϕjmaxELBO=argϕjmaxh∑qϕ(H∣V)⋅logPθ(V,H)+H[q]=argϕjmaxh∑qϕ(H∣V)⋅[−logZ+VTWH+21VTLV+21HTJH]+H[q]=argϕjmax=1 h∑qϕ(H∣V)⋅与h和ϕj都无关,为常数C [−logZ+21VTLV]+h∑qϕ(H∣V)⋅[VTWH+21HTJH]+H[q]=argϕjmaxh∑qϕ(H∣V)⋅[VTWH+21HTJH]+H[q]=argϕjmax(1) h∑qϕ(H∣V)⋅VTWH+(2) 21h∑qϕ(H∣V)⋅HTJH+(3) H[q]
得到如上公式后,我们只需对每个部份进行求导即可得到结果,过程中引入假设(拆分维度)即可更加优化公式,我们以 ( 1 ) (1) (1)为例:
( 1 ) = ∑ h q ϕ ( H ∣ V ) ⋅ V T W H = ∑ h ∏ j ^ = 1 P q ϕ ( H j ^ ∣ V ) ⋅ ∑ i = 1 D ∑ j ^ = 1 P v i w i j ^ h j ^ \begin{align} (1) &= \sum_h q_\phi(H|V) \cdot {V^T W H} = \sum_h \prod_{{\hat j}=1}^{P} q_\phi(H_{\hat j}|V) \cdot \sum_{i=1}^{D} \sum_{{\hat j}=1}^{P} {v_i w_{i{\hat j}} h_{\hat j}} \end{align} (1)=h∑qϕ(H∣V)⋅VTWH=h∑j^=1∏Pqϕ(Hj^∣V)⋅i=1∑Dj^=1∑Pviwij^hj^
我们取出其中的一项,如 i = 1 , j ^ = 2 i = 1, {\hat j} = 2 i=1,j^=2,可以得到:
∑ h ∏ j ^ = 1 P q ϕ ( H j ^ ∣ V ) ⋅ v 1 w 12 h 2 = ∑ h 2 q ϕ ( H 2 ∣ V ) ⋅ v 1 w 12 h 2 ⏟ 提出 h 2 相关项 ⋅ ∑ h , − h 2 ∏ j ^ = 1 , − 2 P q ϕ ( H j ^ ∣ V ) ⏟ = 1 = ∑ h 2 q ϕ ( H 2 ∣ V ) ⋅ v 1 w 12 h 2 = q ϕ ( H 2 = 1 ∣ V ) ⋅ v 1 w 12 ⋅ 1 + q ϕ ( H 2 = 0 ∣ V ) ⋅ v 1 w 12 ⋅ 0 = ϕ 2 v 1 w 12 \begin{align} \sum_h \prod_{{\hat j}=1}^{P} q_\phi(H_{\hat j}|V) \cdot {v_1 w_{12} h_{2}} &= \underbrace{\sum_{h_2} q_\phi(H_2|V) \cdot {v_1 w_{12} h_{2}}}_{\text{提出$h_2$相关项}} \cdot \underbrace{\sum_{h, -h_2} \prod_{{\hat j}=1, -2}^{P} q_\phi(H_{\hat j}|V)}_{=1} \\ &= \sum_{h_2} q_\phi(H_2|V) \cdot {v_1 w_{12} h_{2}} \\ &= q_\phi(H_2 = 1|V) \cdot {v_1 w_{12} \cdot 1} + q_\phi(H_2 = 0|V) \cdot {v_1 w_{12} \cdot 0} \\ &= \phi_2 {v_1 w_{12}} \end{align} h∑j^=1∏Pqϕ(Hj^∣V)⋅v1w12h2=提出h2相关项 h2∑qϕ(H2∣V)⋅v1w12h2⋅=1 h,−h2∑j^=1,−2∏Pqϕ(Hj^∣V)=h2∑qϕ(H2∣V)⋅v1w12h2=qϕ(H2=1∣V)⋅v1w12⋅1+qϕ(H2=0∣V)⋅v1w12⋅0=ϕ2v1w12
所以 ( 1 ) (1) (1)的求和结果就应该是 ∑ i = 1 D ∑ j ^ = 1 P ϕ j ^ v i w i j ^ \sum_{i=1}^{D} \sum_{{\hat j}=1}^{P} \phi_{\hat j} v_i w_{i{\hat j}} ∑i=1D∑j^=1Pϕj^viwij^,同理可得 ( 2 ) , ( 3 ) (2), (3) (2),(3)结果为:
{ ( 1 ) = ∑ i = 1 D ∑ j ^ = 1 P ϕ j ^ v i w i j ^ ( 2 ) = ∑ j ^ = 1 P ∑ m = 1 , − j P ϕ j ^ ϕ m J j ^ m + C ( 3 ) = − ∑ j = 1 P [ ϕ j log ϕ j + ( 1 − ϕ j ) log ( 1 − ϕ j ) ] \begin{cases} (1) = \sum_{i=1}^{D} \sum_{{\hat j}=1}^{P} \phi_{\hat j} v_i w_{i{\hat j}} \\ (2) = \sum_{{\hat j}=1}^{P} \sum_{m=1, -j}^{P} \phi_{\hat j} \phi_m J_{{\hat j}m} + C \\ (3) = - \sum_{j=1}^P \left[ \phi_j \log \phi_j + (1-\phi_j) \log (1-\phi_j) \right] \\ \end{cases} ⎩ ⎨ ⎧(1)=∑i=1D∑j^=1Pϕj^viwij^(2)=∑j^=1P∑m=1,−jPϕj^ϕmJj^m+C(3)=−∑j=1P[ϕjlogϕj+(1−ϕj)log(1−ϕj)]
通过求导又可得:
{ ∇ ϕ j ( 1 ) = ∑ i = 1 D v i w i j ∇ ϕ j ( 2 ) = ∑ m = 1 , − j P ϕ m J j m ∇ ϕ j ( 3 ) = − log ϕ j 1 − ϕ j \begin{cases} \nabla_{\phi_j} (1) = \sum_{i=1}^{D} v_i w_{ij} \\ \nabla_{\phi_j} (2) = \sum_{m=1, -j}^{P} \phi_m J_{jm} \\ \nabla_{\phi_j} (3) = - \log \frac{\phi_j}{1 - \phi_j} \\ \end{cases} ⎩ ⎨ ⎧∇ϕj(1)=∑i=1Dviwij∇ϕj(2)=∑m=1,−jPϕmJjm∇ϕj(3)=−log1−ϕjϕj
根据 ∇ ϕ j ( 1 ) + ∇ ϕ j ( 2 ) + ∇ ϕ j ( 3 ) = 0 \nabla_{\phi_j} (1) + \nabla_{\phi_j} (2) + \nabla_{\phi_j} (3) = 0 ∇ϕj(1)+∇ϕj(2)+∇ϕj(3)=0可得:
ϕ j = σ ( ∑ i = 1 D v i w i j + ∑ m = 1 , − j P ϕ m J j m ) \phi_j = \sigma(\sum_{i=1}^{D} v_i w_{ij} + \sum_{m=1, -j}^{P} \phi_m J_{jm}) ϕj=σ(i=1∑Dviwij+m=1,−j∑PϕmJjm)
由于 ϕ j \phi_j ϕj用于表示每一个维度的数据,所以我们可以使用 ϕ = { ϕ j } j = 1 P \phi = \{\phi_j\}_{j=1}^{P} ϕ={ϕj}j=1P通过坐标上升的方法进行求解。
相关文章:

28 玻尔兹曼机
文章目录 28 玻尔兹曼机28.1 模型定义28.2 梯度推导28.3 梯度上升28.4 基于VI[平均场理论]求解后验概率 28 玻尔兹曼机 28.1 模型定义 玻尔兹曼机是一张无向图,其中的隐节点和观测节点可以有任意连接如下图: 我们给其中的节点、连线做出一些定义&#…...
命令提示符之操作基础(Windows)
打开命令提示符 方法一 打开指定文件的文件夹,在路径栏里输入“cmd”,回车,就进入控制台了。默认路径就是指定文件夹的路径。 方法二 打开指定的文件夹,按住shift键,在空白处右击,在菜单栏中选择“在此处打…...
【C语言】初识C语言+进阶篇导读
✨个人主页: Anmia.🎉所属专栏: C Language 🎃操作环境: Visual Studio 2019 版本 本篇目的是面向编程新手,没接触过编程的人。以及C进阶的导读。 内容是C语言重要知识点的简单解释,不做详解。给…...

wxWidgets学习笔记:wxListCtrl使用详解
使用案例 wxListCtrl中放21个item,每一行放两个item,每个item显示图标和名字,点击某个图标,该图标呈现响应状态并响应对应的事件 以下是使用wxListCtrl实现放置21个item,每一行放两个item,每个item显示图…...

酷炫的python日志库-loguru
Loguru是一个python的日志库,比logging更简单,好用,功能丰富。 GitHub - Delgan/loguru: Python logging made (stupidly) simple 安装 pip install loguru 特征 开箱即用,补样板没有处理程序,没有清理程序ÿ…...

html根据图片变换背景色
html根据图片变换背景色 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title><style>.item {width: 50%;height: 80vh;margin: 0 auto;border: 1px solid red;}</style> </head><body>…...

“深入探究JVM:揭秘Java虚拟机的工作原理“
标题:深入探究JVM:揭秘Java虚拟机的工作原理 摘要:本文将深入探究Java虚拟机(JVM)的工作原理,包括JVM的架构、内存管理、垃圾回收机制以及即时编译等关键概念。通过详细解释这些概念,读者将能够…...
小程序的api使用 以及一些weui组件实列获取头像 扫码等
今日目标 响应式单位rpx小程序的生命周期 【重点】20%小程序框架 weui 【重点】 50%内置API 【重点】30%综合练习 1. 响应式rpx 1.1 rpx单位 rpx是微信小程序提出的一个尺寸单位,将整个手机屏幕宽度分为750份,1rpx 就是 1/750,避免不同手…...
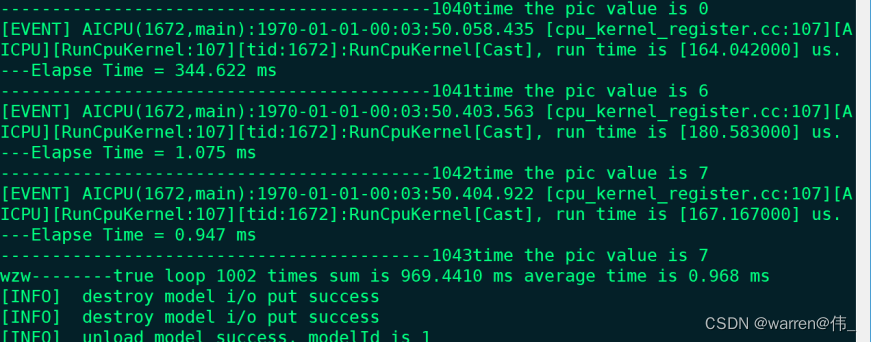
海思ss928部署手写数字识别模型
大致流程--------------------------------------------------------------------------------------------------------------------- 模型转换---------------------------------------------------------------------------------------------------- 1:准备MNI…...

组学知识速递(五)|ChIP-seq知多少?
近段时间来,我们合作的ChIP-Seq技术发表的高分成功案例一篇接一篇,您是否心动了呢?本篇文章,总结了ChIP-Seq实验部分重点知识点,开启ChIP-Seq的你绝不要错过! Q1 什么是ChIP-Seq? ChIP-Seq即染…...

2308C++内存序概略
参考 释放:在释放前的任意读写操作不能放在此操作之后. 获取:在获取后的任意读写操作不能放在此操作之前. 放松:只保证本操作的原子性,一般用于统计. 消费:在加载后的依赖本原子变量的,都不能重排在本操作之前. 获取释放:获取释放 序列一致,完全一致....
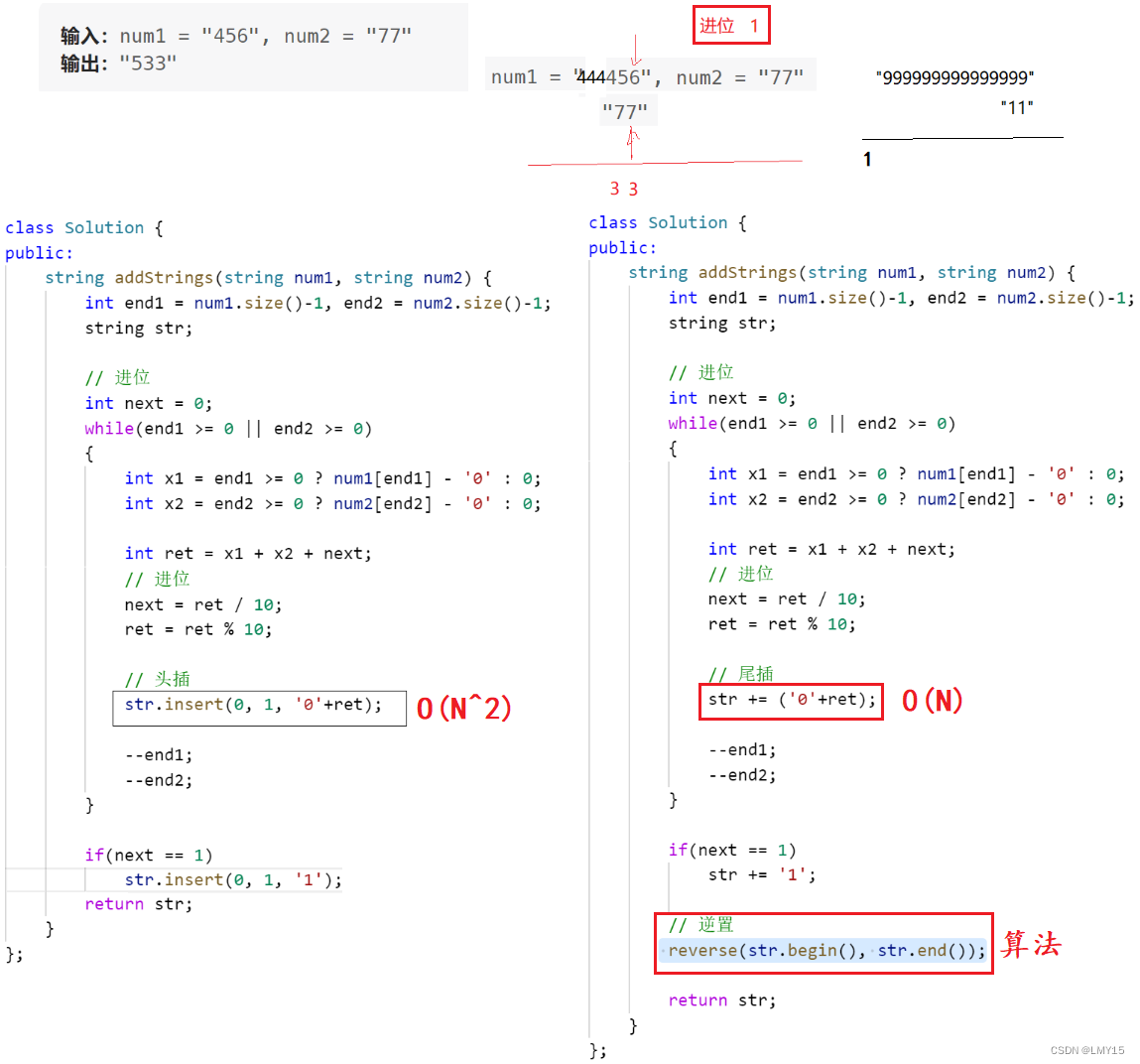
【C++】string的使用
1、string的使用 #define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> #include<string> using namespace std;void Test1() {string s1;string s2("hello");cin >> s1;cout << s1 << endl;//strcat【字符串拼接】string ret1 s…...

Android 周期任务
AlarmManager使用 1.创建意图 // 创建意图,启动MonthlyTaskServiceIntent intent new Intent(getContext(), TimeTaskService.class); // 传递数据intent.putExtra(TimeTaskService.KEY_TITLE,userRemind.getTitle());intent.putExtra(TimeTaskService.KEY_DEC,u…...
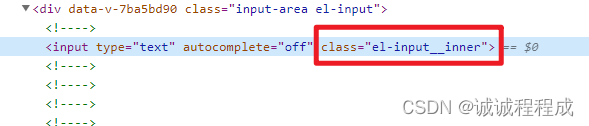
修改第三方组件默认样式
深度选择器 修改el-input的样式: <el-input class"input-area"></el-input>查看DOM结构: 原本使用 /deep/ 但是可能不兼容 使用 :deep .input-area {:deep(.el-input__inner){background-color: blue;} }将 input 框背景色改为…...

【游戏客户端】制作你玩我猜Like玩法
【游戏客户端】制作你玩我猜Like玩法 大家好,我是Lampard猿奋~~ “你画我猜”相信大家都不陌生,当初这款小游戏可谓茶余饭后必玩之选,风头一时无二。今天要和大家分享如何实现一个你玩我猜Like的玩法。 我们可以简单的把需求拆成两个个部分&…...

分页查询从接口到实现,统一对日期类型进行格式化处理
编写Service实现类编写Mapper的sql,但复杂的sql语句需要写到mapper对应的xml文件中日期类型格式化处理 /*** 扩展springmvc框架的消息转换器* param converters*/Overrideprotected void extendMessageConverters(List<HttpMessageConverter<?>> conve…...
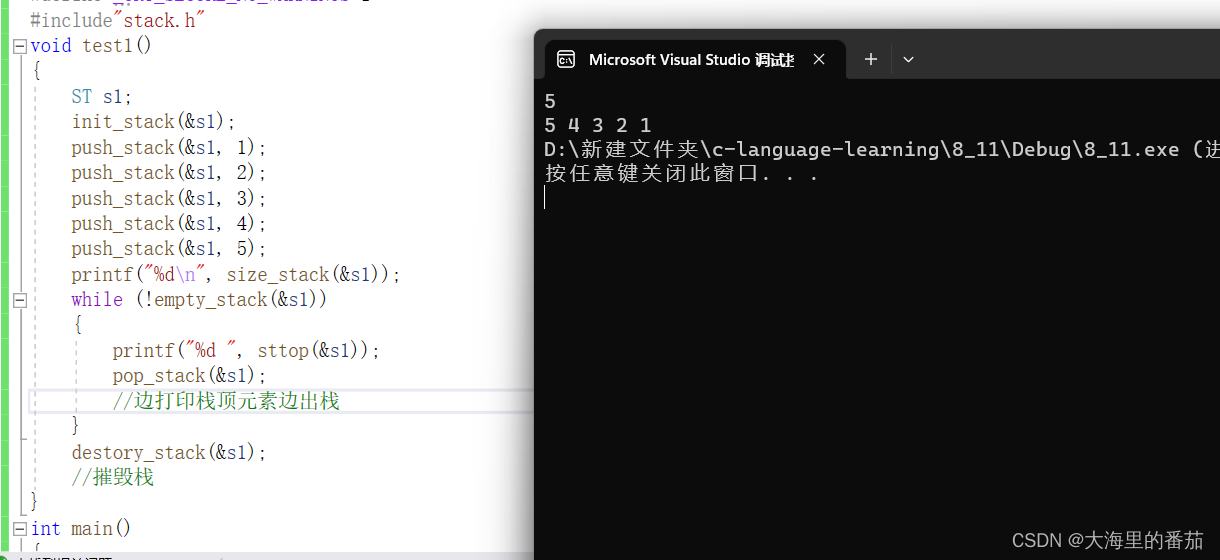
栈和队列详解(1)
目录 一、什么是栈? 二、创建一个我们自己的栈 1.前置准备 1.1需要的三个文件 1.2结构体的创建和头文件的引用 2.接口的实现 2.1初始化栈结构体 2.2尾插(压栈) 2.3栈存放的元素个数和判断栈是否为空 2.4获取栈顶元素 2.5出栈 2.6摧毁栈 2.7测试接口 三、…...

苏州OV泛域名RSA加密算法https
RSA加密算法是一种非对称加密算法,它被广泛应用于信息安全领域。与对称加密算法不同,RSA加密算法使用了两个密钥,一个公钥和一个私钥。公钥可以公开,任何人都可以使用它加密信息,但只有私钥的持有者才能解密信息。RSA加…...

凯迪正大—微机继电保护校验仪
一、继电保护测试仪产品概述 KDJB-802继电保护测试仪是在参照电力部颁发的《微机型继电保护试验装置技术条件(讨论稿)》的基础上,听取用户意见,总结目前国内同类产品优缺点,充分使用现代的微电子技术和器件实现的一种新…...

Linux文件属性与权限管理(可读、可写、可执行)
Linux把所有文件和设备都当作文件来管理,这些文件都在根目录下,同时Linux中的文件名区分大小写。 一、文件属性 使用ls -l命令查看文件详情: 1、每行代表一个文件,每行的第一个字符代表文件类型,linux文件类型包括&am…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...

P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上,小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...

[QMT量化交易小白入门]-六十二、ETF轮动中简单的评分算法如何获取历史年化收益32.7%
本专栏主要是介绍QMT的基础用法,常见函数,写策略的方法,也会分享一些量化交易的思路,大概会写100篇左右。 QMT的相关资料较少,在使用过程中不断的摸索,遇到了一些问题,记录下来和大家一起沟通,共同进步。 文章目录 相关阅读1. 策略概述2. 趋势评分模块3 代码解析4 木头…...
