当前位置： 首页 > news >正文

【密码学】穴居人密码

news 2026/2/10 11:53:21

穴居人密码

文字记载中，有时会把来自古希腊文化之前的各种记录作为密码学的例子，但称它们为密码学一定太不严格了，这是因为那些方法都太原始了。密码学的起源能追溯到多早，取决于你把密码学的相关定义确定得有多宽泛。大多数作者都认为亨利·E·兰根在他的《密码分析—密码学教程》（Cryptanalytics—A Course in Cryptography）中，把密码学起源确定得太早：

早期的史前穴居人可能通过口中发出的声音，或象形标识，形成了一套彼此之间传递消息的系统。

我们更乐意从古代苏美尔的“密码学原型”的例子讲起。苏美尔人信奉很多神，但是只有12个神是“大圈（GreatCircle）”的一部分，其中包括六男六女。

男性 女性

60-Anu 55-Antu

50-Enlil 45-Ninlil

40-Ea/Enki 35-Ninki

30-Nanna/Sin 25-Ningal

20-Utu/Shamash 15-Inanna/Ishtar

10-Ishkur/Adad 5-Ninhursag

每位神对应的编号有时可以代替这位神的名字！，这样我们就得到了一套代换密码。一般来说，尽管在引言中解释过了，当整个单词或名字被更换为数字或字母时，就将其称之为编码而不是密码。

好像每一种发展了书写的文化在此之后不久就孕育出了密码（如果大部分人是文盲，书写本身就提供了某种秘密性）。

参考文献：

1.《密码历史与传奇》 [美] 克雷格·鲍尔（Craig P.Bauer）人民邮电出版社 2019-4-1

相关文章：

【密码学】穴居人密码

穴居人密码 文字记载中，有时会把来自古希腊文化之前的各种记录作为密码学的例子，但称它们为密码学一定太不严格了，这是因为那些方法都太原始了。密码学的起源能追溯到多早，取决于你把密码学的相关定义确定得有多宽泛。大多数作者都…...

编程日记 2023/8/12 3:05:39

neo4j的CQL命令实例演示

天行健，君子以自强不息；地势坤，君子以厚德载物。 每个人都有惰性，但不断学习是好好生活的根本，共勉！ 文章均为学习整理笔记，分享记录为主，如有错误请指正，共同学习进步。…...

编程日记 2023/8/12 3:04:37

vue3+ts使用antv/x6

使用 2.x 版本 x6.antv 新官网: 安装 npm install antv/x6 //"antv/x6": "^2.1.6",项目结构 1、初始化画布 index.vue <template><div id"container"></div> </template><script setup langts> import { onM…...

编程日记 2023/8/12 3:03:37

wsl1 ubuntu通过宿主机代理连接外网

文章目录 环境变量配置apt换源apt安装&#xff0c;测试是否能通外网可能出现的问题&#xff1a;Temporary failure resolving 参考 背景&#xff1a;公司电脑是局域网&#xff0c;通过走代理来连接外网 wsl1 ubuntu想要通过来连接宿主机的局域网代理&#xff0c;访问外网 可以…...

编程日记 2023/8/12 3:02:35

ubuntu20.04 opencv4.2 安装笔记

参考&#xff1a; https://docs.opencv.org/4.x/d7/d9f/tutorial_linux_install.html Build with opencv_contrib # 1. Install minimal prerequisites&#xff0c; libgtk2.0-dev pkg-config 用来显示图像 sudo apt update && sudo apt install -y cmake g wget un…...

编程日记 2023/8/12 3:01:34

ubuntu安装nginx以及php的部署

目录 1.安装依赖包 2.安装nginx 3.编译nginx 4.启动nginx 5.访问nginx 6.增加源地址 7.安装php 8.配置php-fpm 9.修改权限 10.配置nginx里的php 11.启动php-fpm 12.配置php文件以及权限 13.登陆查看 1.安装依赖包 apt-get install gcc apt-get install libpcre3 l…...

编程日记 2023/8/12 3:00:33

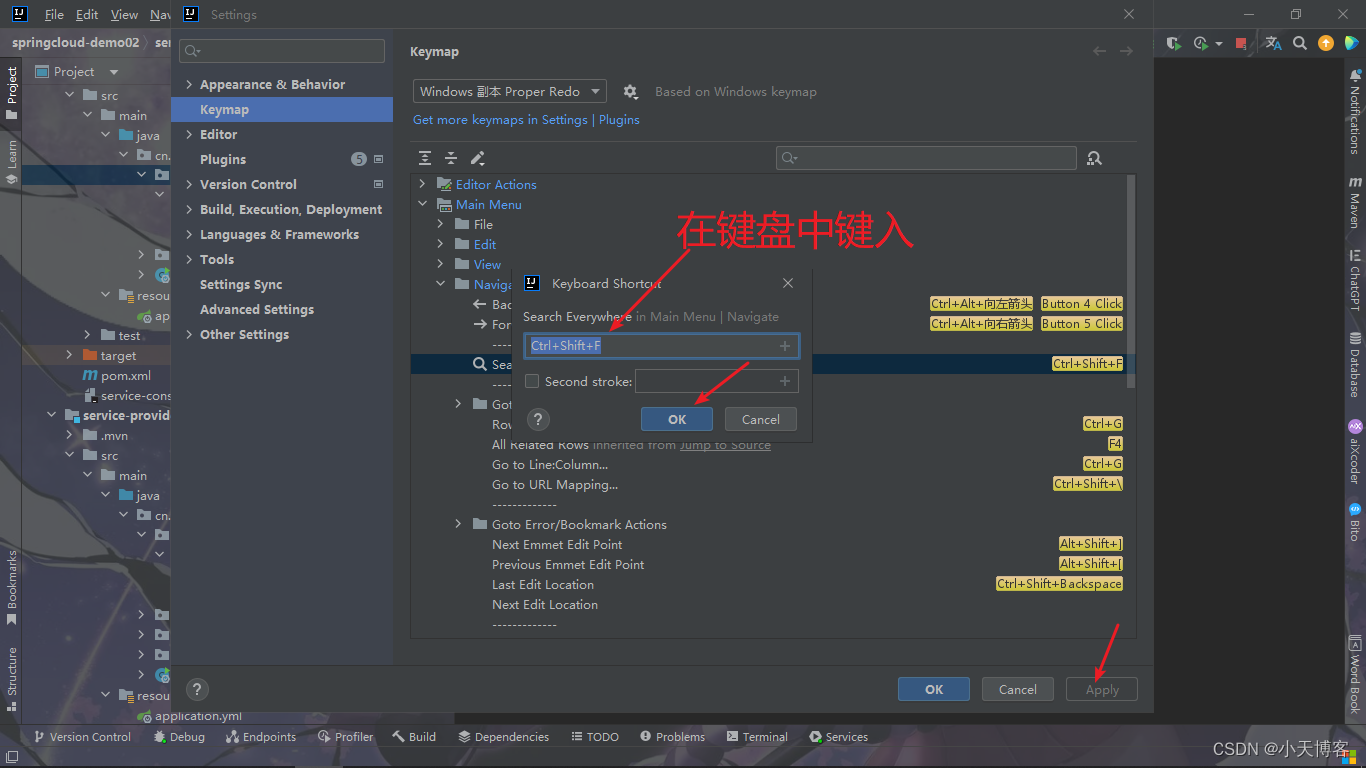
IntelliJ IDEA 2021/2022关闭双击shift全局搜索

我这里演示的是修改&#xff0c;删除是右键的时候选择Remove就好了 IDEA左上角 File-->Settings 找到Navigate -->Search Everywhere &#xff0c;右键添加快捷键。 OK --> Apply应用...

编程日记 2023/8/12 2:59:31

HTML 元素中的name 属性

name 属性是 HTML 元素中常用的属性之一。它用于指定表单元素的名称&#xff0c;以便在提交表单时将其值与对应的键关联起来。 每个表单元素&#xff08;例如 <input>、<select> 和 <textarea>&#xff09;都可以具有一个 name 属性&#xff0c;该属性为元素…...

编程日记 2023/8/12 2:58:30

快速上手React：从概述到组件与事件处理

前言 「作者主页」&#xff1a;雪碧有白泡泡 「个人网站」&#xff1a;雪碧的个人网站 「推荐专栏」&#xff1a; ★java一站式服务 ★ ★ React从入门到精通★ ★前端炫酷代码分享 ★ ★ 从0到英雄&#xff0c;vue成神之路★ ★ uniapp-从构建到提升★ ★ 从0到英雄&#xff…...

编程日记 2023/8/12 2:57:29

K8S系列文章之 离线安装自动化工具Ansible

参考 文档 离线安装 Ansible - DevOps - dbaselife 一、Ansible简介 Ansible是一款开源的IT配置管理工具&#xff0c;常被IT界的小伙伴们用于自动化的场景&#xff0c;多用在服务部署、配置管理方面。配置文件采用最常见的yaml格式&#xff0c;学习起来也是比较容易&#xff…...

编程日记 2023/8/12 2:56:27

mysql8.0.3集群搭建

下载mysql安装包&#xff1a; https://dev.mysql.com/downloads/mysql/5.7.html#downloads 准备环境 1、准备三台服务器并设置hosts 192.168.236.143 mysql1 192.168.236.144 mysql2 192.168.236.145 mysql32、设置免密登陆 #生成秘钥 ssh-keygen -t rsa #一直按Enter即可…...

编程日记 2023/8/12 2:55:25

vue中router路由的原理？两种路由模式如何实现？(vue2) -(上)

平时我们编写路由时&#xff0c;通常直接下载插件使用&#xff0c;在main.js文件中引入直接通过引入vue-router中的Router通过Vue.use使用以后定义一个routeMap数组&#xff0c;里边是我们编写路由的地方&#xff0c;最后通过实例化一个 Router实例 将routes我们定义的routeMao…...

编程日记 2023/8/12 2:54:24

消息队列(3) -封装数据库的操作

前言 上一篇博客我们写了, 关于交换机, 队列,绑定, 写入数据库的一些建库建表的操作 这一篇博客中,我们将建库建表操作,封装一下实现层一个类来供上层服务的调用 , 并在写完该类之后, 测试代码是否完整 实现封装 在写完上述的接口类 与 xml 后, 我们想要 创建一个类 ,来调用…...

编程日记 2023/8/12 2:53:23

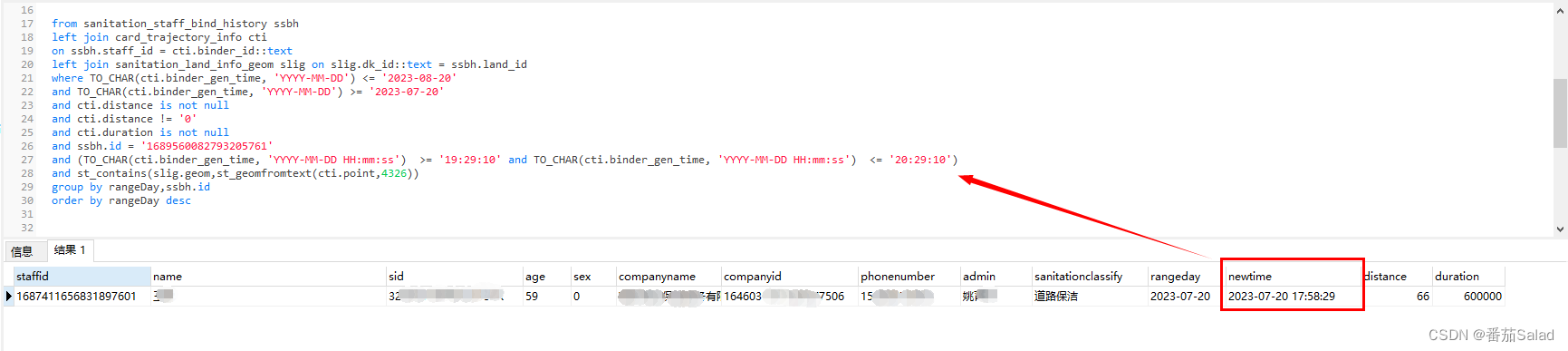
PostgreSQL中根据时间段范围查询数据，如19:29:10到20:29:10范围内的数据，排除年月日

数据格式如下 问题描述 我的SQL语句条件是 WHERE (TO_CHAR(cti.binder_gen_time, YYYY-MM-DD HH:mm:ss) > 19:29:10 AND TO_CHAR(cti.binder_gen_time, YYYY-MM-DD HH:mm:ss) < 20:29:10)为什么我数据的时间是2023-07-20 17:58:29也能被查出来&#xff1f; 问题解决…...

编程日记 2023/8/12 2:52:22

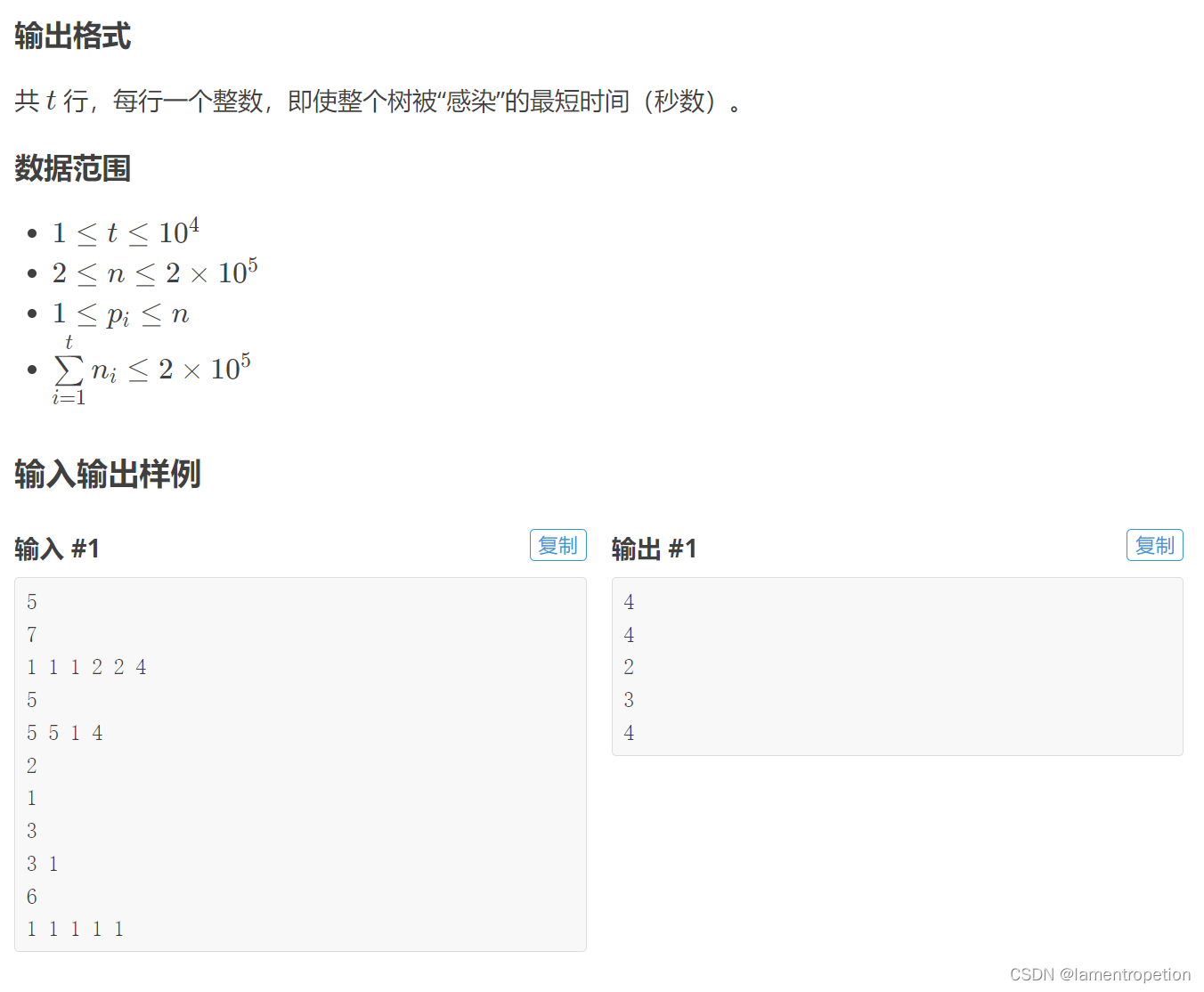
【二分+贪心】CF1665 C

Problem - C - Codeforces 题意&#xff1a; 思路&#xff1a; 一开始想太简单wa6了 只想到先感染大的分量&#xff0c;然后最后把最大的分量剩下的染色 但是可能会有别的分量更大&#xff08;因为最后给最大的染色之后可能不再是最大的&#xff09; 可以用堆维护&#xf…...

编程日记 2023/8/12 2:51:21

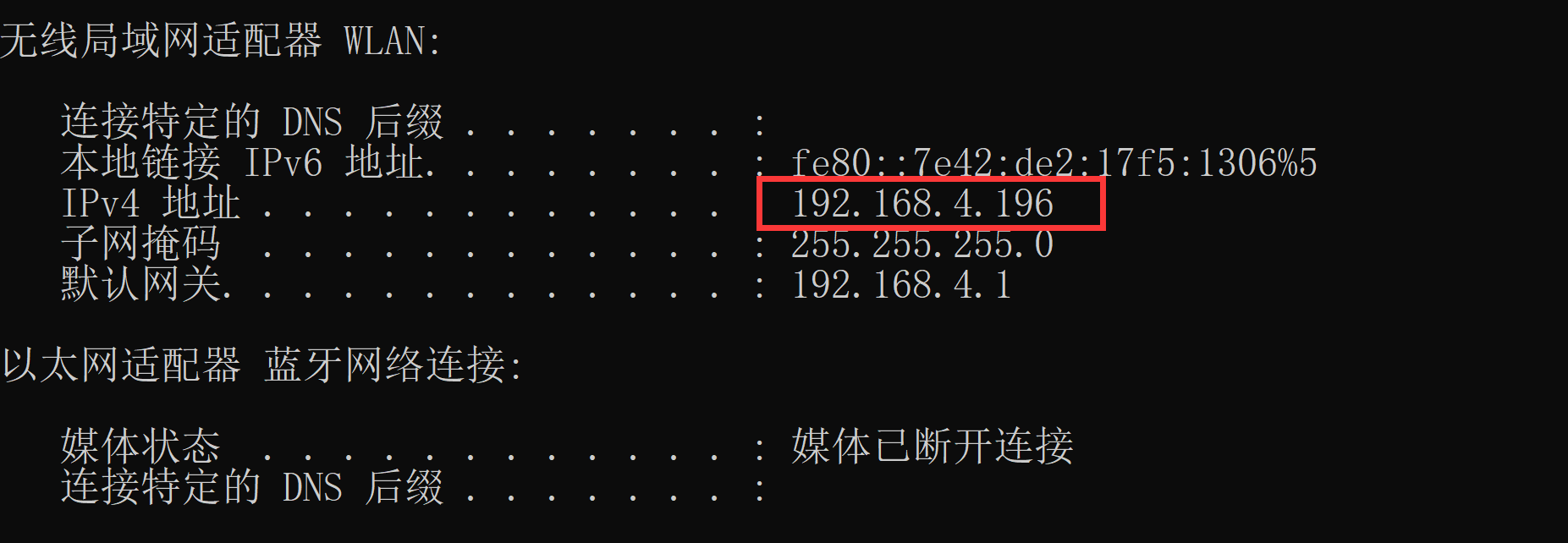
【Wamp】安装 | 局域网内设备访问

安装教程&#xff1a; https://wampserver.site/article/1.html 下载 https://www.wampserver.com/en/ 安装路径上不能有中文 安装好之后图标呈绿色 放入网页文件 将网页文件放置于wamp文件夹的www子文件夹 例如&#xff1a;\Wamp\program\www 修改http端口 WAMP服务器…...

编程日记 2023/8/12 2:50:20

【golang】类型推断和变量重声明

类型推断是一种编程语言在编译期自动解释表达式类型的能力。 1.Go语言的类型推断可以带来哪些好处&#xff1f; 在写代码时&#xff0c;我们通过使用Go语言的类型推断会节省敲击次数&#xff0c;而节省下来的键盘敲击次数几乎可以忽略不记。但它真正的好处&#xff0c;往往会…...

编程日记 2023/8/12 2:49:18

“算法详解”系列第3卷贪心算法和动态规划出版

“算法详解”系列图书共有4卷&#xff0c;目前1到3卷已经出版。最新出版的是第3卷—贪心算法和动态规划。 算法详解 卷3 贪心算法和动态规划 “算法详解”系列图书共有4卷&#xff0c;本书是第3卷—贪心算法和动态规划。其中贪心算法主要包括调度、最小生成树、集群、哈夫曼编…...

编程日记 2023/8/12 2:48:17

CSS前端开发指南：创造精美的用户界面

简介&#xff1a; 《CSS前端开发指南&#xff1a;创造精美的用户界面》是一本旨在帮助读者掌握CSS技术&#xff0c;实现令人惊叹的前端用户界面的实用指南。无论您是初学者还是有经验的开发者&#xff0c;本书都将为您提供全面的知识和实用技巧&#xff0c;帮助您创建引人注目…...

编程日记 2023/8/12 2:47:16

代数学与理论物理中常见的群

代数学与理论物理中常见的群 代数学与理论物理中常见的群 四阶群 六阶群 对称群 二维转动群 三维转动群 三维正交群 群 O3群...

编程日记 2023/8/12 2:46:14

今日学习：Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存

文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

编程新知 2026/1/27 16:41:02

以光量子为例，详解量子获取方式

光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学&#xff08;silicon photonics&#xff09;的光波导&#xff08;optical waveguide&#xff09;芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中&#xff0c;光既是波又是粒子。光子本…...

编程新知 2026/2/7 11:51:32

Linux nano命令的基本使用

参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时&#xff0c;显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

编程新知 2026/1/31 2:17:41

django blank 与 null的区别

1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是&#xff0c;要注意以下几点&#xff1a; Django的表单验证与null无关&#xff1a;null参数控制的是数据库层面字段是否可以为NULL&#xff0c;而blank参数控制的是Django表单验证时字…...

编程新知 2025/7/7 3:34:13

从“安全密码”到测试体系：Gitee Test 赋能关键领域软件质量保障

关键领域软件测试的"安全密码"&#xff1a;Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天&#xff0c;软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力&#xff0c;从金融交易到交通管控&#xff0c;这些关乎国计民生的关键领域…...

编程新知 2026/2/2 20:26:17

小智AI+MCP

什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析&#xff1a;AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github&#xff1a;https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

编程新知 2026/2/8 11:51:37

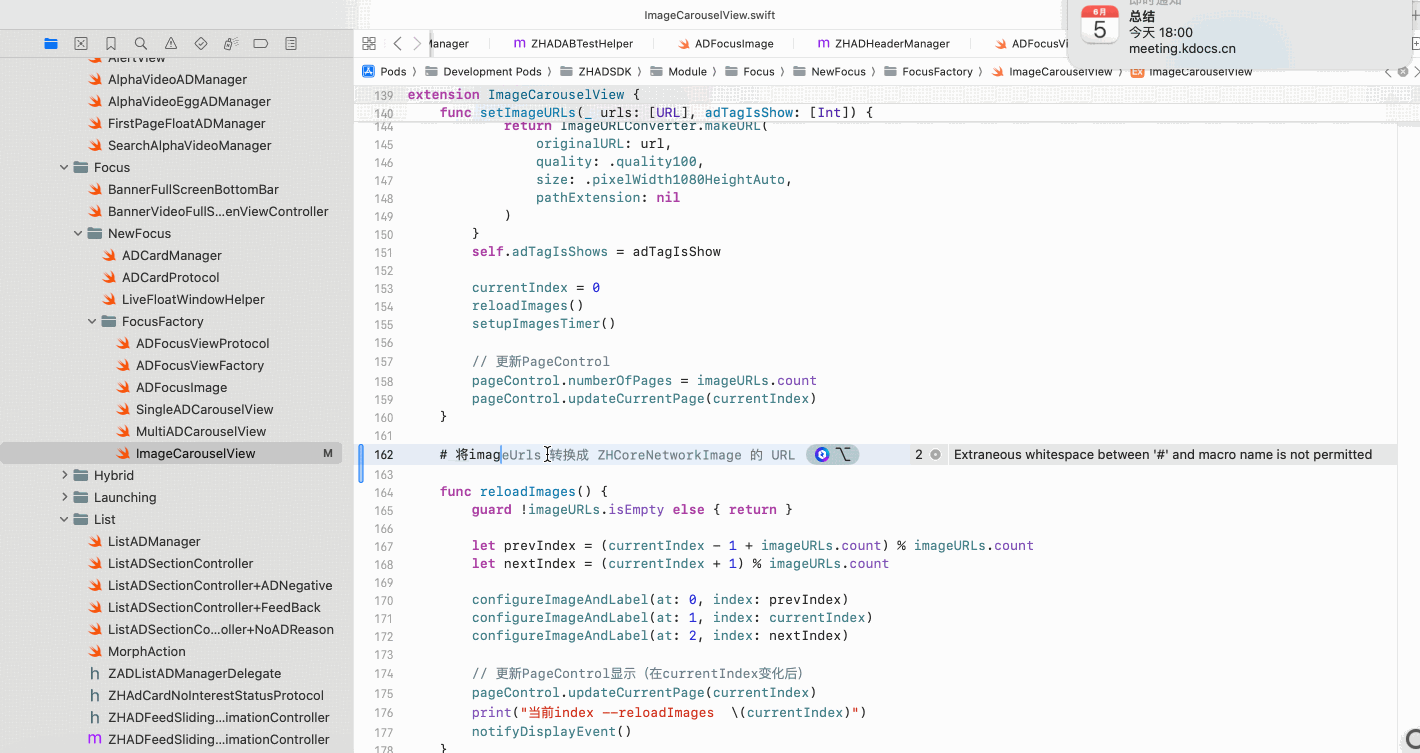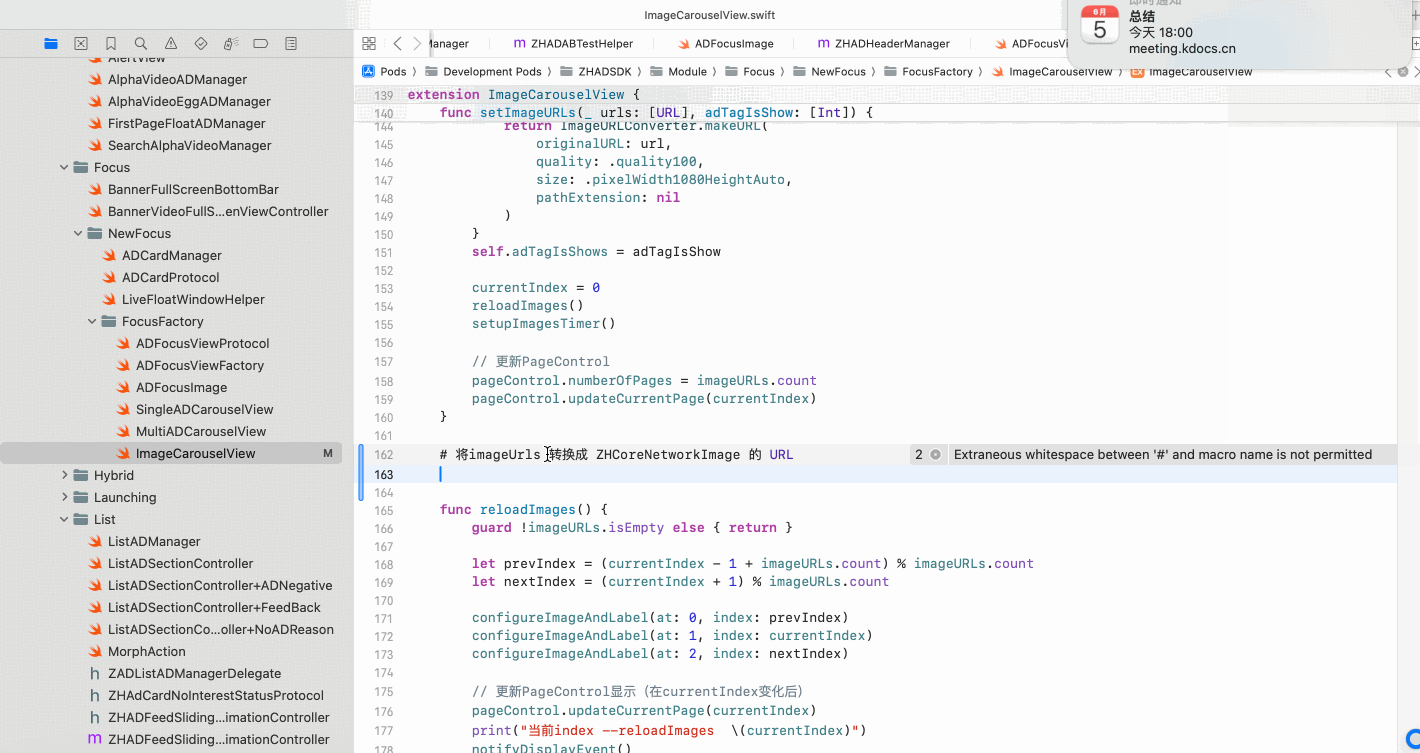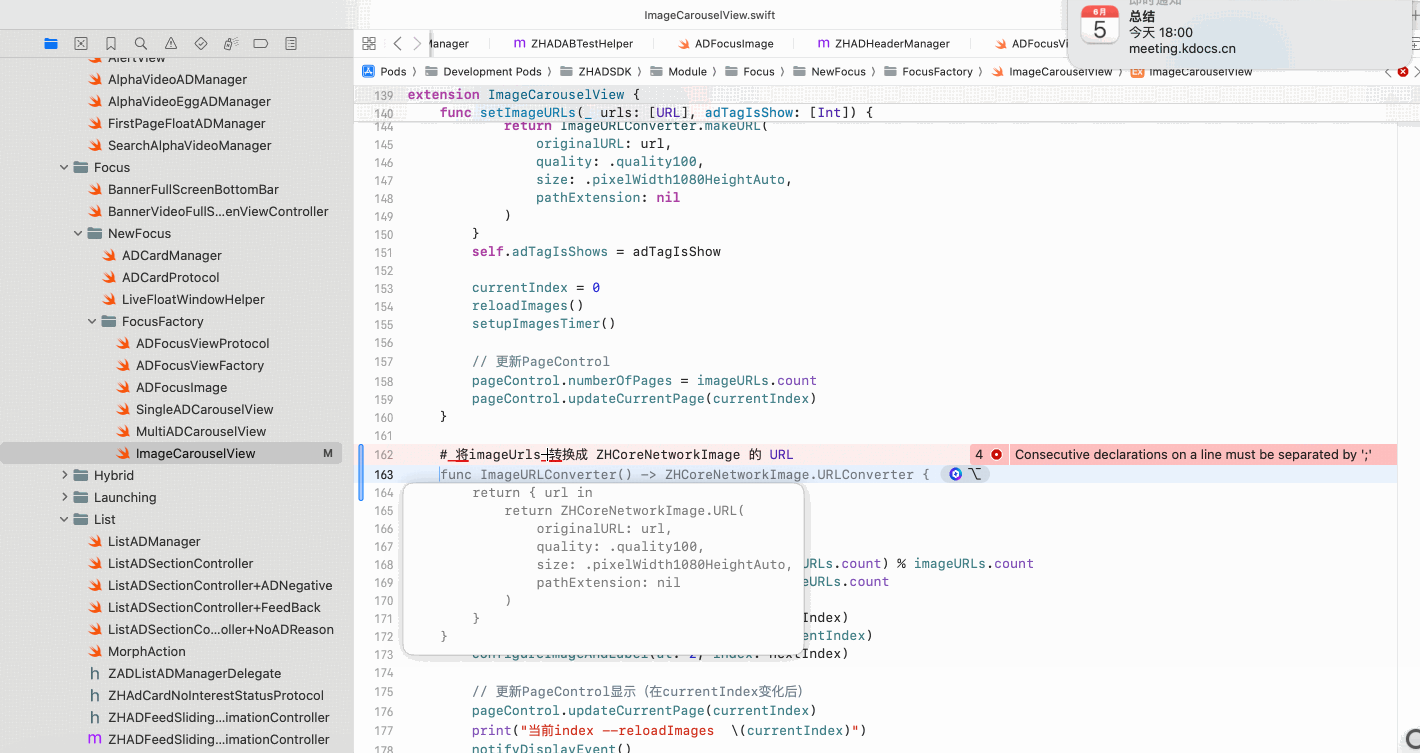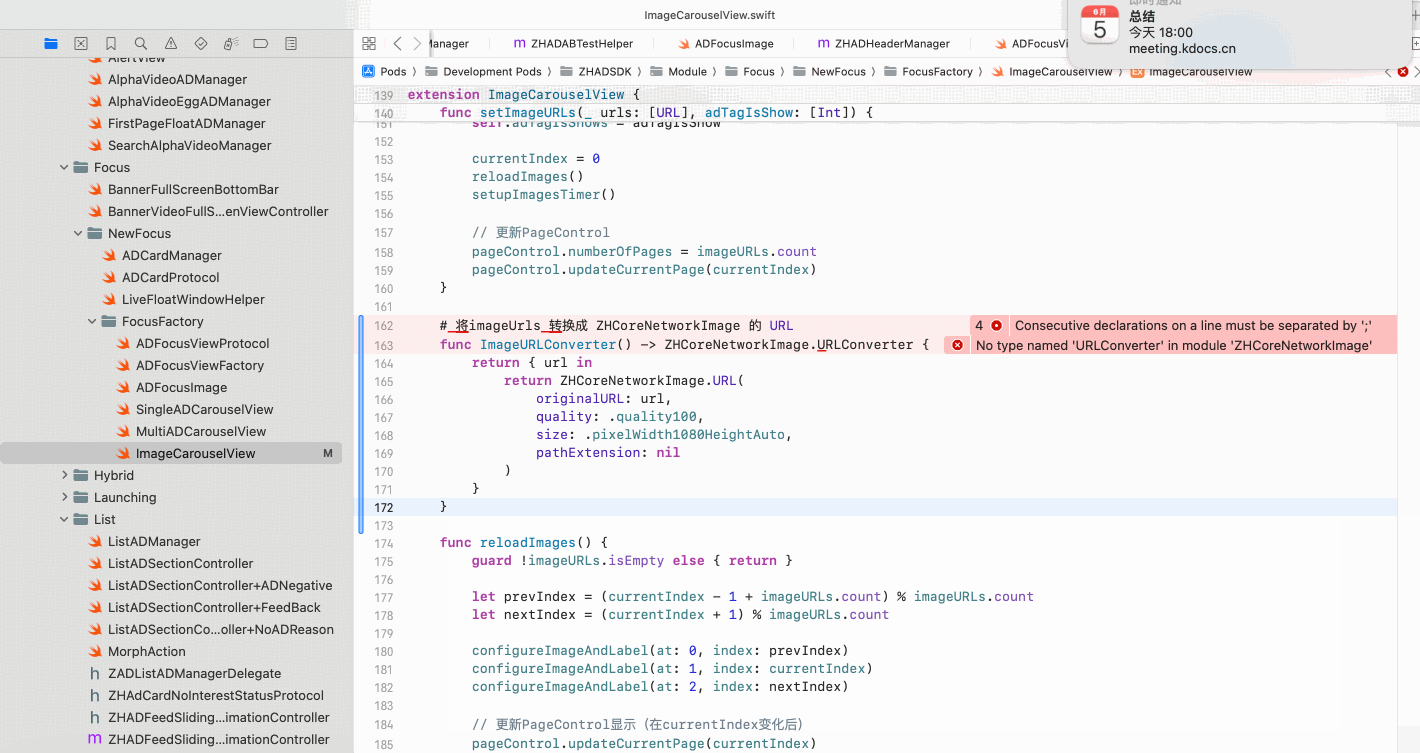
Copilot for Xcode (iOS的 AI辅助编程)

Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot&#xff0c;它能根据上下文补全代码&#xff0c;快速生成常用…...

编程新知 2026/1/26 20:00:58

C#中用于控制自定义特性（Attribute）

我们来详细解释一下 [AttributeUsage(AttributeTargets.Class, AllowMultiple false, Inherited false)] 这个 C# 属性。 在 C# 中&#xff0c;Attribute&#xff08;特性&#xff09;是一种用于向程序元素&#xff08;如类、方法、属性等&#xff09;添加元数据的机制。Attr…...

编程新知 2026/2/9 6:24:59

codeforces C. Cool Partition

目录 题目简述&#xff1a; 思路&#xff1a; 总代码&#xff1a; https://codeforces.com/contest/2117/problem/C 题目简述&#xff1a; 给定一个整数数组&#xff0c;现要求你对数组进行分割&#xff0c;但需满足条件&#xff1a;前一个子数组中的值必须在后一个子数组中…...

编程新知 2025/12/31 1:58:19

HarmonyOS-ArkUI 自定义弹窗

自定义弹窗 自定义弹窗是界面开发中最为常用的一种弹窗写法。在自定义弹窗中&#xff0c; 布局样式完全由您决定&#xff0c;非常灵活。通常会被封装成工具类&#xff0c;以使得APP中所有弹窗具备相同的设计风格。 自定义弹窗具备的能力有 打开弹窗自定义布局&#xff0c;以…...

编程新知 2026/2/7 20:50:09