2023.8.13
atcoder_abc\AtCoder Beginner Contest 310\E_NAND_repeatedly
//题意:给定一个n长度的01串,计算f(l,r)(l<=r,l在1~n,r在1~n)的和,f的计算(ai,a(i+1))运算,有0就为1,11为0
//若f(l,r)=1,则f(l,r-1)为0或sr为0,即只取决于上一位的情况和当前位,枚举右端点,对答案的贡献即有多少左端点使得f(i,r)=1;
#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>#include<unordered_map>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define int128 __int128_t#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define fer(i,x) for(int i=e.head[x];i;i=e.next[i])#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;ll poww(ll x, ll k){if(k == 1) return x;if(k == 0) return 1;ll tmp = poww(x, k / 2);if(k & 1) return tmp * tmp % mod * x % mod;return tmp * tmp % mod;}template<size_t size>struct Road{int to[size], next[size], head[size], cnt = 1;ll w[size];void add(int x, int y, ll ww){to[cnt] = y;w[cnt] = ww;next[cnt] = head[x];head[x] = cnt ++;}void clear(int n){for(int i = 0; i <= n; i ++){head[i] = 0;}cnt = 1;}};template<size_t size>struct Combinatorial_number{int fact[size], finv[size]; // fact[x]是x的阶乘,inv[x]是fact[x]的逆元void init(){fact[0] = 1;for(int i = 1; i < (int)size; i ++){fact[i] = 1ll * fact[i - 1] * i % mod;}finv[size - 1] = poww(fact[size - 1], mod - 2);for(int i = size - 2; i >= 0; i --){finv[i] = 1ll * finv[i + 1] * (i + 1) % mod;}}ll C(int n, int m){if(m < n || n < 0 || m < 0) return 0;return 1ll * fact[m] * finv[n] % mod * finv[m - n] % mod;}ll A(int n, int m){if(m < n || n < 0 || m < 0) return 0;return 1ll * fact[m] * finv[m - n] % mod;}ll llC(int n, int m){//求解不进行取余mod的可能爆longlong的C(n,m)值;if(m < n || n < 0 || m < 0) return 0;swap(n, m);long long sum = 1;if (m > n - m) m = n - m;n = n - m + 1;for (int i = 1; i <= m; i ++){sum *= n ++;sum /= i;}return sum;}};template<size_t size>struct Prime{int con[size], tot = 0, vis[size];void init(){for(int i = 2; i < (int)size; i ++){if(vis[i] == 0) con[++ tot] = i;for(int j = 1; j <= tot && i * con[j] < (int)size; j ++){vis[i * con[j]] = con[j];if(i % con[j] == 0) break;}}}};// Road <N> e; // 无向图 * 2// Combinatorial_number <N> comb;// Prime <N> prime;//题意:给定一个n长度的01串,计算f(l,r)(l<=r,l在1~n,r在1~n)的和,f的计算(ai,a(i+1))运算,有0就为1,11为0//若f(l,r)=1,则f(l,r-1)为0或sr为0,即只取决于上一位的情况和当前位,枚举右端点,对答案的贡献即有多少左端点使得f(i,r)=1;//int n,m;int a[N];int dp[N][2]; //dp[i][0/1]表示f(l,i)==0的数量或f(l,i)==1的数量void solve(){cin>>n;string s;cin>>s;s=" "+s;int ans=0;fr(i,1,s.size()-1){if(s[i]=='0'){dp[i][0]=1; //本身dp[i][1]=dp[i-1][0]+dp[i-1][1]; //考虑上一位有多少f(l,i-1)==0的数量或f(l,i-1)==1的数量}else{dp[i][0]=dp[i-1][1];dp[i][1]=dp[i-1][0]+1;}ans+=dp[i][1];}cout<<ans<<'\n';}signed main(){int t=1;// cin>>t;while(t--) solve();return 0;}atcoder_abc\AtCoder Beginner Contest 313\D_Odd_or_Even
//题意:交互题,给定n,可以选择k个数(k为奇数且k<n),程序告诉k个数的异或值,求可以唯一确定的n长度序列(数值只会为0或1)
//思路:以n=4,k=3为例,先查询1 2 3,1 3 4,1 2 4三个结果的异或值,将三个结果异或就可以得知a1的值,同理,前k+1个数也可推出
//要知道第k+2个数,查询3,4..k+2的异或值,再异或a3,a4...ak+1即可
//k为奇数是为了保证在k次查询中除查询的其他均出现偶数次
#include <bits/stdc++.h>using namespace std;using LL = long long;int main(void) {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n, k;cin >> n >> k;vector<int> ans(n);auto solve = [&](int l, int r) {vector<int> tmp(r - l);vector<int> q;for (int i = l; i < r; ++i) {q.clear();for (int j = l; j < r; ++j)if (j != i)q.push_back(j);cout << "?";for (auto& i : q)cout << ' ' << i + 1;cout << endl;cin >> tmp[i - l];}for (int i = l; i < r; ++i) {for (int j = l; j < r; ++j) {if (j != i) {ans[i] ^= tmp[j];}}}};solve(0, k + 1);for (int i = k + 1; i < n; i++) {cout << "?";for (int j = i; j > i - k; --j) {cout << ' ' << j + 1;}cout << endl;cin >> ans[i];for (int j = i - 1; j > i - k; --j)ans[i] ^= ans[j];}cout << "!";for (auto& i : ans)cout << ' ' << i;cout << endl;return 0;}//题意:给定一个字符串,由()?组成,可以将?替换成(或),求能组成满足()的个数
//状态:dp[i][j]表示在i位置,(记作1,)表示-1,j表示前缀和
#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>#include<unordered_map>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define int128 __int128_t#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;ll poww(ll x, ll k){if(k == 1) return x;if(k == 0) return 1;ll tmp = poww(x, k / 2);if(k & 1) return tmp * tmp % mod * x % mod;return tmp * tmp % mod;}template<size_t size>struct Road{int to[size], next[size], head[size], cnt = 1;ll w[size];void add(int x, int y, ll ww){to[cnt] = y;w[cnt] = ww;next[cnt] = head[x];head[x] = cnt ++;}void clear(int n){for(int i = 0; i <= n; i ++){head[i] = 0;}cnt = 1;}};template<size_t size>struct Combinatorial_number{int fact[size], finv[size]; // fact[x]是x的阶乘,inv[x]是fact[x]的逆元void init(){fact[0] = 1;for(int i = 1; i < (int)size; i ++){fact[i] = 1ll * fact[i - 1] * i % mod;}finv[size - 1] = poww(fact[size - 1], mod - 2);for(int i = size - 2; i >= 0; i --){finv[i] = 1ll * finv[i + 1] * (i + 1) % mod;}}ll C(int n, int m){if(m < n || n < 0 || m < 0) return 0;return 1ll * fact[m] * finv[n] % mod * finv[m - n] % mod;}ll A(int n, int m){if(m < n || n < 0 || m < 0) return 0;return 1ll * fact[m] * finv[m - n] % mod;}ll llC(int n, int m){//求解不进行取余mod的可能爆longlong的C(n,m)值;if(m < n || n < 0 || m < 0) return 0;swap(n, m);long long sum = 1;if (m > n - m) m = n - m;n = n - m + 1;for (int i = 1; i <= m; i ++){sum *= n ++;sum /= i;}return sum;}};template<size_t size>struct Prime{int con[size], tot = 0, vis[size];void init(){for(int i = 2; i < (int)size; i ++){if(vis[i] == 0) con[++ tot] = i;for(int j = 1; j <= tot && i * con[j] < (int)size; j ++){vis[i * con[j]] = con[j];if(i % con[j] == 0) break;}}}};// Road <maxn> e; // 无向图 * 2// Combinatorial_number <N> comb;// Prime <N> prime;//题意:给定一个字符串,由()?组成,可以将?替换成(或),求能组成满足()的个数int n,m;int a[N];int dp[3010][3010]; //dp[i][j]表示在i位置,(记作1,)表示-1,j表示前缀和void solve(){string s;cin>>s;n=s.size();s=' '+s;dp[0][0]=1;int Max=0;fr(i,1,n){fr(j,0,i){if(s[i]=='('){if(j)dp[i][j]=dp[i-1][j-1];}else if(s[i]==')'){dp[i][j]=dp[i-1][j+1];}else {if(!j) dp[i][j]=dp[i-1][j+1];else dp[i][j]=(dp[i-1][j+1]+dp[i-1][j-1])%mod;}}}cout<<dp[n][0]<<'\n';}signed main(){int t=1;// cin>>t;while(t--) solve();return 0;}相关文章:

2023.8.13
atcoder_abc\AtCoder Beginner Contest 310\E_NAND_repeatedly //题意:给定一个n长度的01串,计算f(l,r)(l<r,l在1~n,r在1~n)的和,f的计算(ai,a(i1))运算,有0就为1,11为0 //若f(l,r)1,则f(l,r-1)为0或sr为0,即只取决于上一位的情况和当前位ÿ…...

kvm not all arguments converted during string
kylin virt-manager 远程镜像制作问题记录(not all arguments ) 项目场景: 服务器端安装的OS版本:Kylin-Server-10-SP1-Release-Build20-20210518-arm64-2021-05-18 客户端安装的OS版本:Kylin-Server-10-SP1-Release-Build20-20210518-x86_…...

JVM 基础
巩固基础,砥砺前行 。 只有不断重复,才能做到超越自己。 能坚持把简单的事情做到极致,也是不容易的。 JVM 类加载机制 JVM 类加载机制分为五个部分:加载,验证,准备,解析,初始化&am…...

智谷星图赵俊:让人才和区块链产业“双向奔赴”丨对话MVP
区块链产业需要什么样的人才?赵俊很有发言权。 赵俊是北京智谷星图科技有限公司的技术总监,也是FISCO BCOS官方认证讲师。他2017年接触区块链,随后选择人才培育领域深耕。“为区块链行业引进更多人才这件事很有价值,跟我的职业理…...
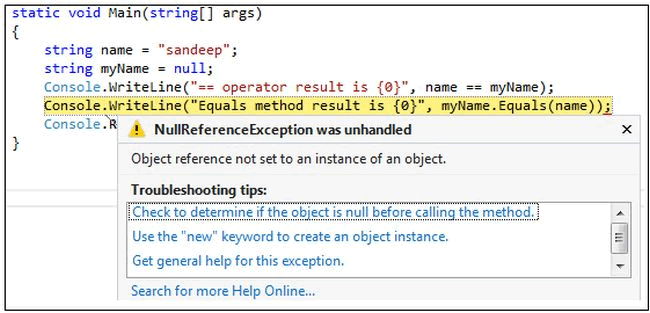
C# Equals()方法报错:NullReferenceException was unhandled
下面是一个C# Equals()方法的例子,执行时报错了 static void Main(string[] args) {string name "sandeep";string myName null;Console.WriteLine(" operator result is {0}", name myName);Console.WriteLine("Equals method result…...
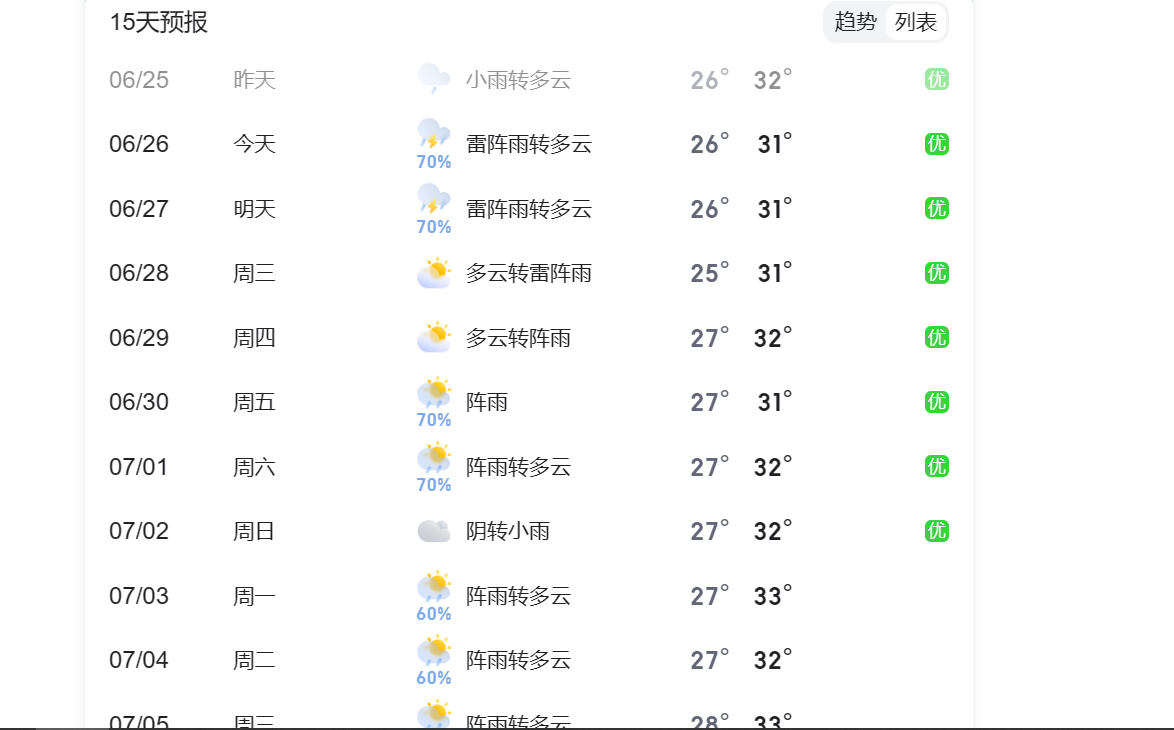
Linux下C语言调用libcurl库获取天气预报信息
一、概述 当前文章介绍如何在Linux(Ubuntu)下使用C语言调用libcurl库获取天气预报的方法。通过HTTP GET请求访问百度天气API,并解析返回的JSON数据,可以获取指定城市未来7天的天气预报信息。 二、设计思路 【1】使用libcurl库进…...

“深入解析JVM:Java虚拟机原理和内部结构“
标题:深入解析JVM:Java虚拟机原理和内部结构 摘要:本文将深入解析JVM(Java虚拟机)的原理和内部结构。我们将从JVM的基础概念开始,逐步介绍其组成部分,包括类加载器、运行时数据区、字节码解释器…...
 返回的list不能add,remove)
Arrays.asList() 返回的list不能add,remove
一.Arrays.asList() 返回的list不能add,remove Arrays.asList()返回的是List,而且是一个定长的List,所以不能转换为ArrayList,只能转换为AbstractList 原因在于asList()方法返回的是某个数组的列表形式,返回的列表只是数组的另一个视图,而数组本身并没…...
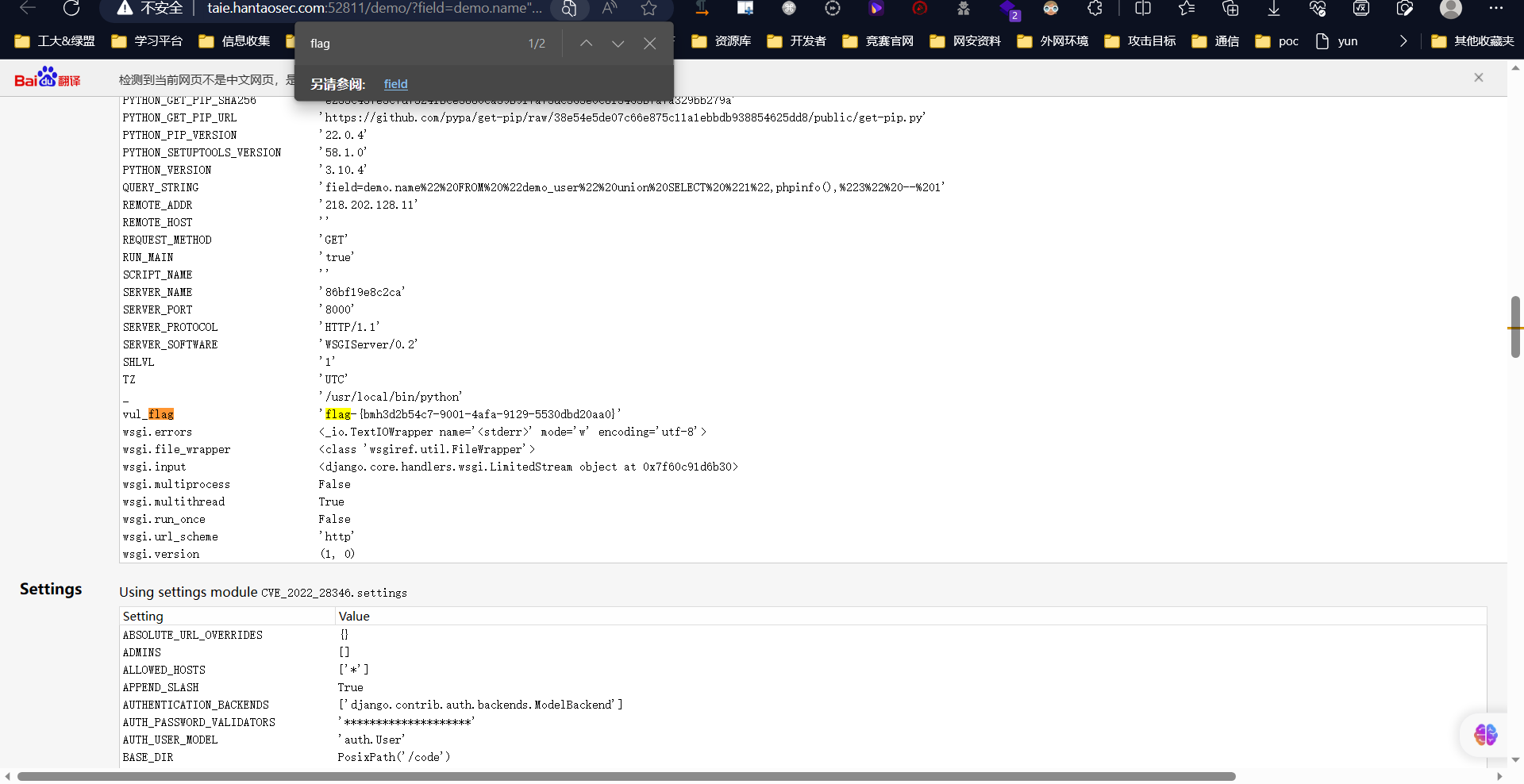
命令执行漏洞
1、命令执行漏洞 1.1、简介 Django是用Python开发的一个免费开源的Web结构,几乎包括了Web使用方方面面,能够用于快速建立高性能、文雅的网站,Diango提供了许多网站后台开发常常用到的模块,使开发者可以专注于业务部分。 1.2、漏…...

Hive 中 sort by 和 order by 的区别
文章目录 数据量大小区别作用范围 在 Hive 中, SORT BY 和 ORDER BY 都用于对查询结果进行排序,但它们在实现方式和适用场景上有一些区别。 数据量大小区别 SORT BY: SORT BY 用于在 Hive 中对查询结果进行排序,它的主要特点是在…...

网络资源利用最大化:爬虫带宽优化解决方案
大家好,作为一名专业的爬虫程序员,我们都知道在爬取大量数据的过程中,网络带宽是一个十分宝贵的资源。如果我们不合理地利用网络带宽,可能会导致爬虫任务的效率低下或者不稳定。今天,我将和大家分享一些优化爬虫带宽利…...

STDF - 基于 Svelte 和 Tailwind CSS 打造的移动 web UI 组件库,Svelte 生态里不可多得的优秀项目
Svelte 是一个新兴的前端框架,组件库不多,今天介绍一款 Svelte 移动端的组件库。 关于 STDF STDF 是一个移动端的 UI 组件库,主要用来开发移动端 web 应用。和我之前介绍的很多 Vue 组件库不一样,STDF 是基于近来新晋 js 框架 S…...
C语言一些有趣的冷门知识
文章目录 概要1.访问数组元素的方法运行结果 2.中括号的特殊用法运行结果 3.大括号的特殊用法运行结果 4.sizeof的用法运行结果 5.渐进运算符运行结果 小结 概要 本文章只是介绍一些有趣的C语言知识,纯属娱乐。这里所有的演示代码我是使用的编译器是Visual Studio …...

Oracle数据库审计
1.什么是审计 审计是用来监控和记录用户的数据库操作的 2.审计级别 语句审计权限审计对象审计 3.查看审计功能是否开启: show parameter audit;相关参数: audit_file_destOS中审计信息存放位置audit_sys_operations默认值为FALSE,即不审…...

Node.js新手在哪儿找小项目练手?
前言 可以参考一下下面的nodejs相关的项目,希望对你的学习有所帮助,废话少说,让我们直接进入正题>> 1、 NodeBB Star: 13.3k 一个基于Node.js的现代化社区论坛软件,具有快速、可扩展、易于使用和灵活的特点。它支持多种数…...
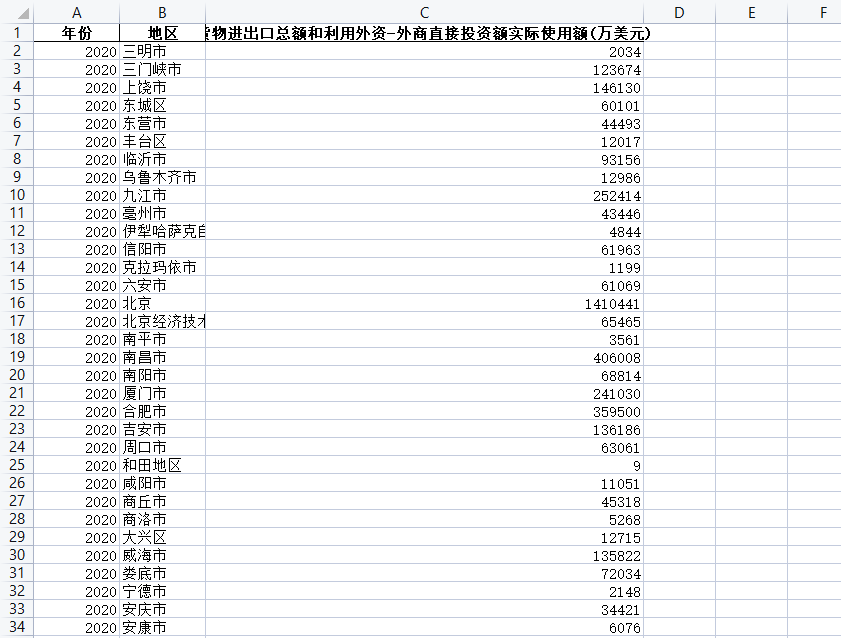
全国各城市-货物进出口总额和利用外资-外商直接投资额实际使用额(1999-2020年)
最新数据显示,全国各城市外商直接投资额实际使用额在过去一年中呈现了稳步增长的趋势。这一数据为研究者提供了对中国外商投资活动的全面了解,并对未来投资趋势和政策制定提供了重要参考。 首先,这一数据反映了中国各城市作为外商投资的热门目…...

CentOS 7查看磁盘空间
CentOS如何查看硬盘大小 CentOS是一种基于Linux的操作系统,主要用于服务器端应用。在服务器管理中,硬盘大小是一个非常重要的指标,查看硬盘大小可以帮助系统管理员有效地管理硬盘空间和避免硬盘满了的情况。 方法一:使用df命令 …...

基于PHP的轻量级博客typecho
本文完成于 5 月中旬,发布时未在最新版本上验证; 什么是 typecho ? Typecho 是一款基于 PHP 的博客软件,旨在成为世界上最强大的博客引擎。Typecho 在 GNU 通用公共许可证 2.0 下发布。支持多种数据库,原生支持 Markdo…...
MySQL多表查询
1.创建student和score表 创建score表 2.为student表和score表增加记录 向student表插入记录的INSERT语句如下: 向score表插入记录的INSERT语句如下: 1.查询student表的所有记录 2.查询student表的第2条到4条记录 3.从student表查询所有学生的学号&#…...
 - 定义服务器类)
消息队列(12) - 定义服务器类
目录 前言设计思想 前言 之前,我们写了通信协议的具体设计,接下来我们设计服务器类 设计思想 我们先只考虑一个虚拟主机的情况下, 在一个虚拟主机的情况下,我们需要有一个session会话来帮助我们存储信息,并且既然是网络通信,那么socket关键字肯定也必不可少,我们在引入一个线…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
