Leetcode 剑指 Offer II 039. 直方图最大矩形面积
题目难度: 困难
原题链接
今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复
剑指offer2就能看到该系列当前连载的所有文章了, 记得关注哦~
题目描述
给定非负整数数组 heights ,数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:

- 输入:heights = [2,1,5,6,2,3]
- 输出:10
- 解释:最大的矩形为图中红色区域,面积为 10
示例 2:
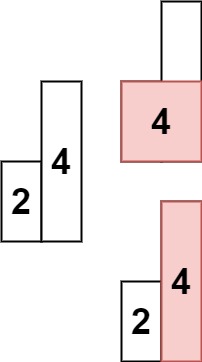
- 输入: heights = [2,4]
- 输出: 4
提示:
- 1 <= heights.length <=10^5
- 0 <= heights[i] <= 10^4
题目思考
- 如何优化时间复杂度?
解决方案
思路
- 分析题目, 最容易想到的思路是暴力两层循环, 具体做法如下:
- 外层循环遍历每个柱子, 记录其高度 h
- 内层向左右两边扩展, 直到超出数组范围或低于当前柱子, 记录对应的下标 l 和 r
- 此时即为使用当前柱子高度时的矩形, 计算其面积 (r-l-1)*h 并更新最终结果
- 这样遍历完成后就覆盖了所有可能的矩形, 其最大面积即为所求
- 暴力算法虽然简单, 但其时间复杂度达到了 O(N^2), 根据题目输入规模, 肯定会超时, 如何优化呢?
- 我们的目的是计算所有矩形的面积, 而高度是已知的, 如何快速得到每个柱子的左右边界呢?
- 由于柱子的左右边界需低于当前柱子, 而且我们既需要知道高度, 又需要知道宽度(下标), 所以这里可以采用单调栈存下标的方式实现, 具体做法如下:
- 单调栈存柱子下标, 且保证从栈顶到栈底的高度递减
- 遍历某个柱子时, 先将其与栈顶高度比较
- 如果栈顶更高, 则将栈顶弹出, 保证单调性, 同时栈顶对应的矩形面积也可以计算了, 其右边界就是当前柱子, 左边界就是栈顶下面一个元素或者-1(对应栈顶左边没有更低柱子的情况),
右-左-1就是矩形的宽 - 否则就退出循环, 将当前柱子压入栈中, 此时栈顶到栈底的高度仍是递减的
- 如果栈顶更高, 则将栈顶弹出, 保证单调性, 同时栈顶对应的矩形面积也可以计算了, 其右边界就是当前柱子, 左边界就是栈顶下面一个元素或者-1(对应栈顶左边没有更低柱子的情况),
- 遍历完所有柱子后, 栈中仍可能存在一些柱子, 此时说明这些柱子右边没有更高的柱子, 其右边界就是数组长度, 左边界和上面情况一样, 依次将其弹出并计算面积
- 最终结果就是上述所有矩形面积的最小值
- 利用单调栈, 我们使用和暴力算法一样的思路计算所有矩形面积, 但却将时间复杂度成功降低到了 O(N), 因为每个柱子只需要处理两次(一次入栈一次出栈)
- 下面的代码就对应了上面的整个过程, 并且有详细的注释, 方便大家理解
复杂度
- 时间复杂度 O(N): 数组每个元素最多处理 2 遍 (压入和弹出栈)
- 空间复杂度 O(N): 栈最多存 N 个元素
代码
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:# stack存储柱子的下标, 且其高度满足从栈顶到栈底递减stack = []res = 0for r, h in enumerate(heights):while stack and heights[stack[-1]] > h:# 栈顶高度大于当前高度, 可以计算栈顶柱子对应的矩形面积了# 栈顶柱子的右边界r就是当前下标, 左边界l是上一个栈顶或-1(上一个栈顶不存在时)ch = heights[stack.pop()]l = -1 if not stack else stack[-1]# 宽*高res = max(res, (r - l - 1) * ch)stack.append(r)# 如果遍历结束后栈中仍有元素, 则说明这些柱子右边没有比它更低的柱子了, 需要计算它们对应的矩形面积while stack:ch = heights[stack.pop()]# 栈顶柱子的右边界r就是数组长度, 左边界l是上一个栈顶或-1(上一个栈顶不存在时)r = len(heights)l = -1 if not stack else stack[-1]# 宽*高res = max(res, (r - l - 1) * ch)return res
大家可以在下面这些地方找到我~😊
我的 GitHub
我的 Leetcode
我的 CSDN
我的知乎专栏
我的头条号
我的牛客网博客
我的公众号: 算法精选, 欢迎大家扫码关注~😊

相关文章:

Leetcode 剑指 Offer II 039. 直方图最大矩形面积
题目难度: 困难 原题链接 今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 给定非负整数数组 heights ,数组中的数字用来表示柱状…...

SpringBoot案例-部门管理-修改
目录 前言 查看页面原型,明确需求 页面原型 需求 阅读接口文件 思路分析 功能接口开发 控制层(Controller类) 业务层(Service类) 业务类 业务实现类 持久层(Mapper类) 接口测试 前…...
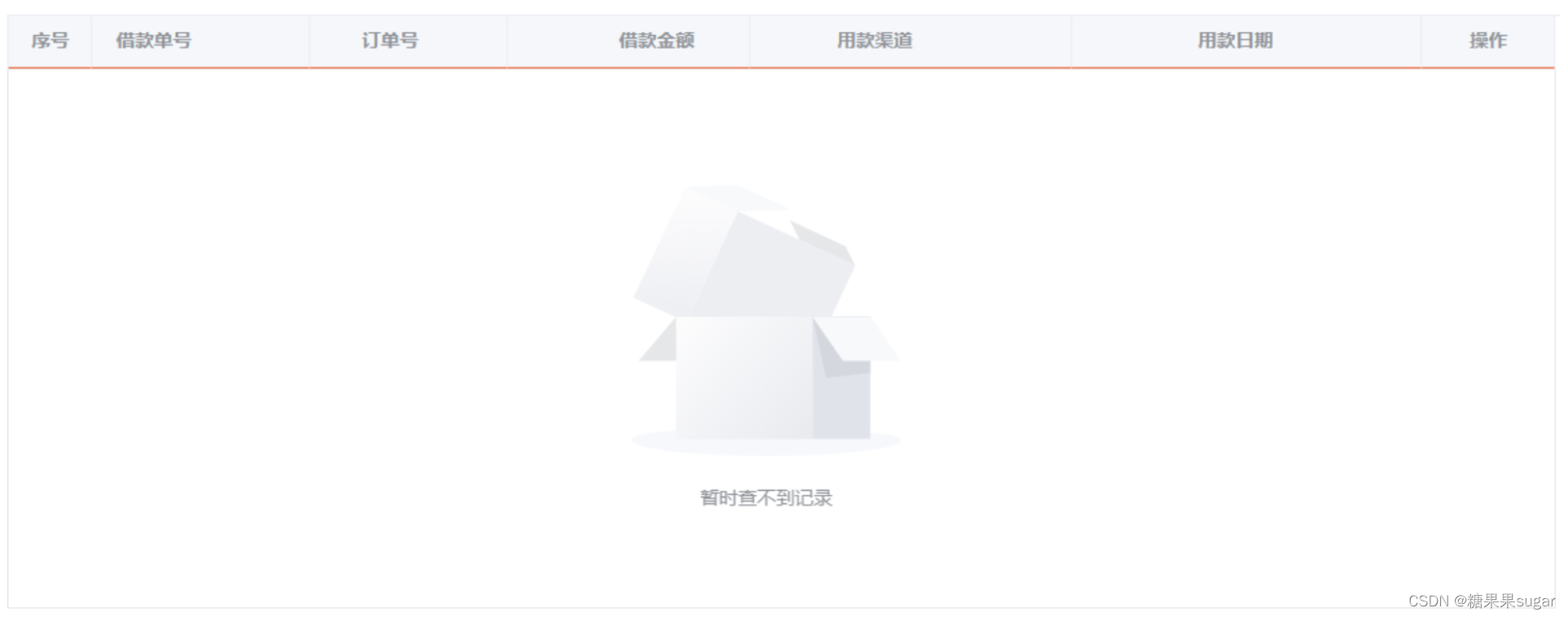
element-ui表格数据为空,图片占位提示
当表格的绑定数据为空时常需要显示暂无数据等字样,这时候就用到了empty-text <el-table:data"tableData"stripeborderempty-text"暂无数据"> 但,当数据为空,想用图片展示呢,如下图 方法一:…...

C++ STL vector 模拟实现
✅<1>主页:我的代码爱吃辣 📃<2>知识讲解:C之STL 🔥<3>创作者:我的代码爱吃辣 ☂️<4>开发环境:Visual Studio 2022 💬<5>前言:上次我们已经数字会用…...

51单片机学习--红外遥控(外部中断)
需要利用下面这个红外接收头,OUT口会发出红外信号对应的高低电平,由于发送的速度很快,所以需要把OUT引脚接在外部中断引脚上,当OUT一旦产生下降沿,马上进中断,这样响应会更及时。 外部中断引脚位于P3_2和P…...
后端开发10.规格模块
概述 简介 效果图...
腾讯出了一个新聊天软件M8
众所周知,如今国内互联网,微信和QQ无疑是社交领域的霸主。 下载:https://www.123pan.com/s/BP5A-RW4xh.html 不过,它们也有各自局限性,比如难以结识新朋友、功能过于复杂等。 这让用户产生厌倦,再加上近几年AI、元宇…...
C++ QT(一)
目录 初识QtQt 是什么Qt 能做什么Qt/C与QML 如何选择Qt 版本Windows 下安装QtLinux 下安装Qt安装Qt配置Qt Creator 输入中文配置Ubuntu 中文环境配置中文输入法 Qt Creator 简单使用Qt Creator 界面组成Qt Creator 设置 第一个Qt 程序新建一个项目项目文件介绍项目文件*.pro样式…...

微信小程序时钟
微信小程序自定义时钟,模拟翻牌时钟。1、页面布局 <view class"date-time-box"><view class"date-box">{{nowDate}}</view><view class"time-box"><view><image class"pic01 {{move[0]?move…...

HttpRunner自动化工具之设置代理和请求证书验证
httprunner设置代理: httprunner 库本身没有提供设置代理的接口,但是底层使用了urllib.requests 等库,可以设置HTTP_PROXY 和HTTPS_PROXY 环境变量,常用的网络库会自动识别这些环境变量。 日常调试使用代理(如charles…...
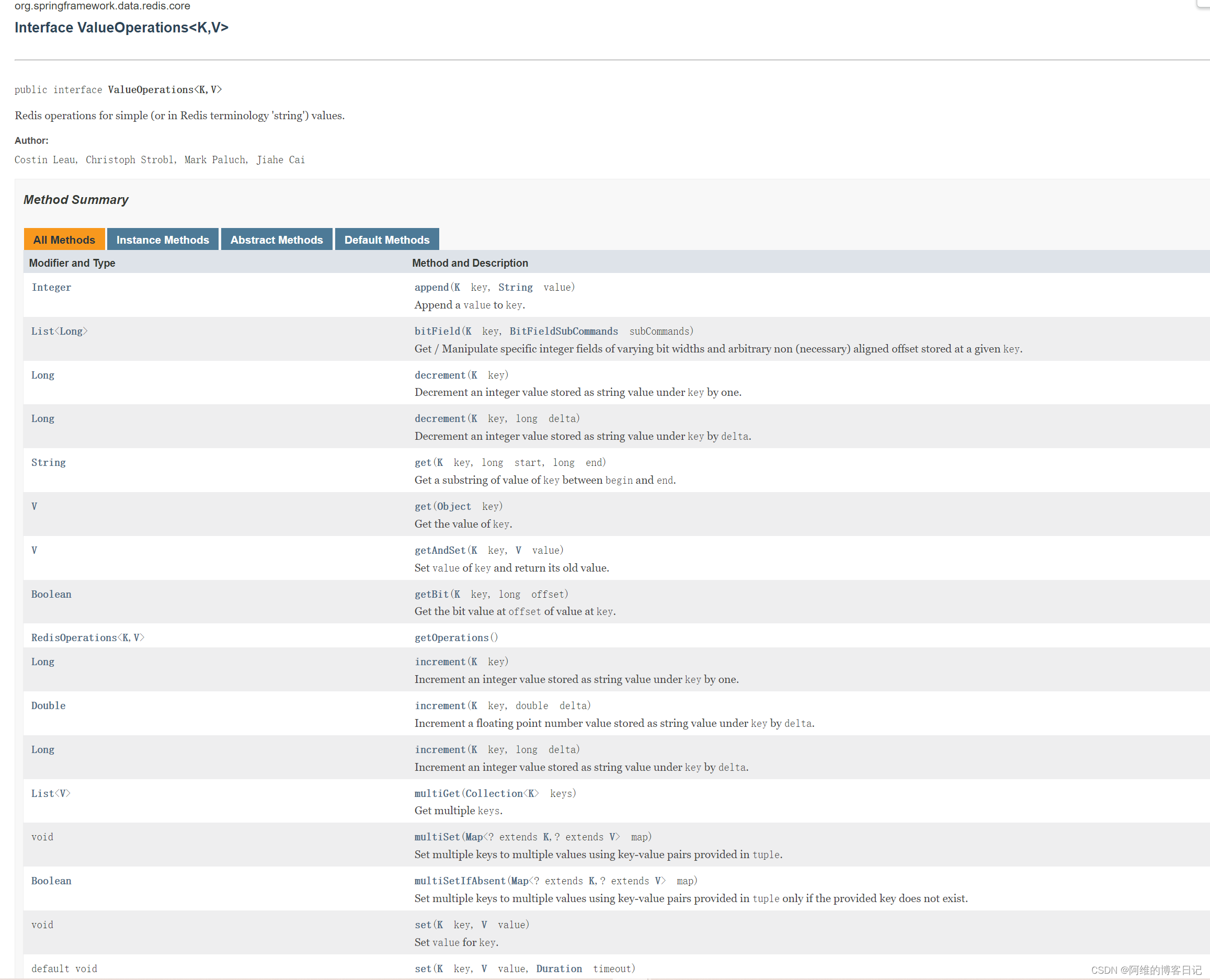
opsForHash() 与 opsForValue 请问有什么区别?
👉:🔗官方API参考手册 如图,opsForHash()返回HashOperations<K,HK,HV>但是 opsForValue()返回ValueOperations<K,V>… 区别就是opsForHash的返回值泛型中有K,HK,HV,其中K是Redis指定的某个数据库里面某一个关键字(由…...
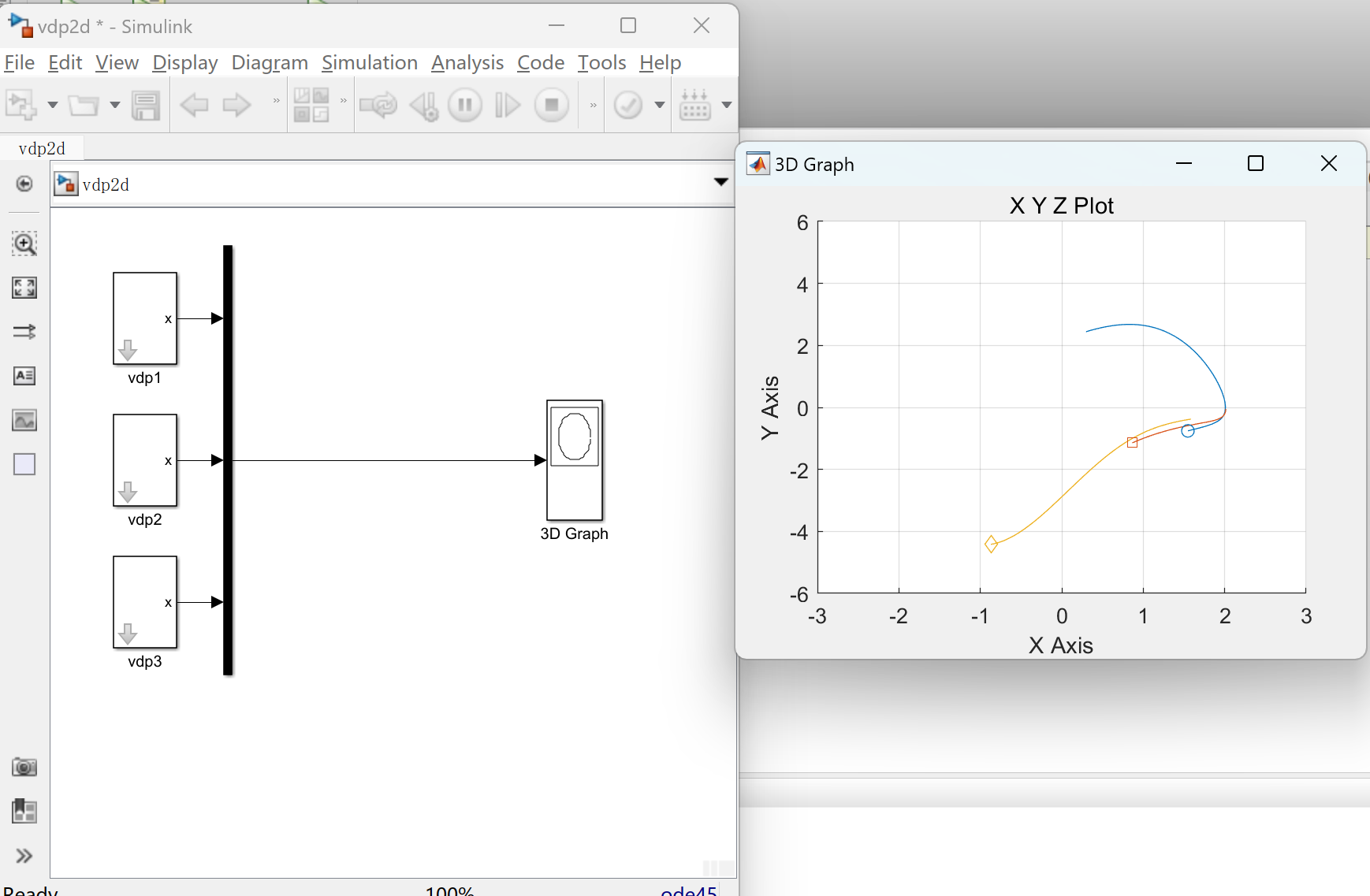
具有吸引子的非线性系统(MatlabSimulink实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Linux一些常见的命令
1. 基础命令 1. ls: 列出目录内容。- 例如:ls -l 以长格式列出文件和目录。2. cd: 切换工作目录。- 例如:cd /home/user 进入 /home/user 目录。3. pwd: 显示当前工作目录的路径。4. mkdir: 创建新目录。-…...

正则表达式的基本知识
正则表达式是一种用于匹配和操作字符串的强大工具。它是由一系列字符和特殊符号组成的模式,可以用来检查字符串是否符合某种模式,进行匹配、替换、提取等操作。 下面是一些常见的正则表达式元字符和语法: 1. 字符匹配: - 普通…...

如何⽤webpack 来优化前端性能
如何⽤webpack 来优化前端性能? ⽤webpack 优化前端性能是指优化 webpack 的输出结果,让打包的最终结果在浏览器运⾏快速⾼效。 压缩代码:删除多余的代码、注释、简化代码的写法等等⽅式。可以利⽤webpack的 UglifyJsPlugin 和 ParallelUgl…...

人机交互中的混合多重反馈
人机交互中态、势、感、知的混合多重反馈是指在交互过程中综合运用不同方面的反馈信息,包括用户态度(态)、行为动势(势)、情感体验(感)和认知反馈(知)。这种多重反馈可以…...

CSS:服务器字体 与 响应式布局(用法 + 例子 + 效果)
文章目录 服务器字体定义 服务器字体使用例子 响应式布局设备类型设备特性例子 服务器字体 解决字体不一致而产生的。 首先,在网上把字体下载好。 定义 服务器字体 font-face{font-family:字体名称;src:url(字体资源路径); }使用 在需要使用的选择器里加上 font…...

24届近3年上海电力大学自动化考研院校分析
今天给大家带来的是上海电力大学控制考研分析 满满干货~还不快快点赞收藏 一、上海电力大学 学校简介 上海电力大学(Shanghai University of Electric Power),位于上海市,是中央与上海市共建、以上海市管理为主的全日…...
PostgreSQL查询慢sql原因和优化方案
PostgreSQL sql查询慢优化方案有一下几种解决方案: 1.关闭会话 查询慢sql的执行会话,关闭进程。 查看数据库后台连接进程 SELECT count(*) FROM pg_stat_activity;SELECT * FROM pg_stat_activity; 查看数据库后台连接进程,但是此条SQL不…...

Leetcode 21. 合并两个有序链表
题目描述 题目链接:https://leetcode.cn/problems/merge-two-sorted-lists/description/ 思路 两个链表都是升序链表,新建一个链表,引入伪头节点作为辅助节点,将各节点添加到伪节点之后,再用一个cur节点指向新链表的…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
