ID3 决策树
西瓜数据集D如下:
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 2 | 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 3 | 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 4 | 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 5 | 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 6 | 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 7 | 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 是 |
| 8 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 9 | 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
| 10 | 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 否 |
| 11 | 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 12 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 否 |
| 13 | 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 14 | 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 15 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 否 |
| 16 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
| 17 | 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
即集合D为分类问题,分类瓜的好坏是一个二分类问题,故|y| =2 ,故只存在p1,p2
信息熵为衡量信息混乱程度的量
记好瓜比例为p1,坏瓜比例为p2
1. 若全是好瓜 , 则 p 1 = 1 , p 2 = 0 E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k = − ( p 1 l o g 2 p 1 + p 2 l o g 2 p 2 ) = 1 ⋅ l o g 2 ⋅ 1 + 0 ⋅ l o g 2 ⋅ 0 = 0 2. 若全是好瓜 , 则 p 1 = 0 , p 2 = 1 E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k = − ( p 1 l o g 2 p 1 + p 2 l o g 2 p 2 ) = 0 ⋅ l o g 2 ⋅ 0 + 1 ⋅ l o g 2 ⋅ 1 = 0 则完全不混乱为全是好瓜或全是坏瓜 , E n t ( D ) = 0 2. 若全是好坏瓜个一半 , 则 p 1 = 1 2 , p 2 = 1 2 E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k = − ( p 1 l o g 2 p 1 + p 2 l o g 2 p 2 ) = − ( 1 2 ⋅ l o g 2 ⋅ 1 2 + 1 2 ⋅ l o g 2 ⋅ 1 2 ) = 1 则最混乱为 E n t ( D ) = 1 1.若全是好瓜,则p_1=1,p_2=0 \\ Ent(D) = -\sum\limits _{k=1}^{|y|}p_klog_2p_k \\= -(p_1log_2p_1 + p_2log_2p_2 ) \\=1\cdot log_2\cdot 1 + 0\cdot log_2\cdot 0 \\=0\\ 2.若全是好瓜,则p_1=0,p_2=1 \\ Ent(D) = -\sum\limits _{k=1}^{|y|}p_klog_2p_k \\= -(p_1log_2p_1 + p_2log_2p_2 ) \\=0\cdot log_2\cdot 0 + 1\cdot log_2\cdot 1 \\=0\\ 则完全不混乱为全是好瓜或全是坏瓜,Ent(D) = 0\\ 2.若全是好坏瓜个一半,则p_1=\frac12,p_2=\frac12 \\ Ent(D) = -\sum\limits _{k=1}^{|y|}p_klog_2p_k \\= -(p_1log_2p_1 + p_2log_2p_2 ) \\=-(\frac12\cdot log_2\cdot \frac12 + \frac12\cdot log_2\cdot \frac12 )\\=1\\ 则最混乱为Ent(D) = 1 1.若全是好瓜,则p1=1,p2=0Ent(D)=−k=1∑∣y∣pklog2pk=−(p1log2p1+p2log2p2)=1⋅log2⋅1+0⋅log2⋅0=02.若全是好瓜,则p1=0,p2=1Ent(D)=−k=1∑∣y∣pklog2pk=−(p1log2p1+p2log2p2)=0⋅log2⋅0+1⋅log2⋅1=0则完全不混乱为全是好瓜或全是坏瓜,Ent(D)=02.若全是好坏瓜个一半,则p1=21,p2=21Ent(D)=−k=1∑∣y∣pklog2pk=−(p1log2p1+p2log2p2)=−(21⋅log2⋅21+21⋅log2⋅21)=1则最混乱为Ent(D)=1
当前样本集合D中第k类样本所占比例为pk(k=1,2,3,…,|y|),则D的信息熵为:
E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k Ent(D) = -\sum\limits _{k=1}^{|y|}p_klog_2p_k Ent(D)=−k=1∑∣y∣pklog2pk
信息增益为:
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a) = Ent(D) - \sum\limits _{v=1}^V \frac{|Dv|}{|D|}Ent(D^v) Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
import math
D = [
['青绿','蜷缩','浊响','清晰','凹陷','硬滑','是'],
['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑','是'],
['乌黑','蜷缩','浊响','清晰','凹陷','硬滑','是'],
['青绿','蜷缩','沉闷','清晰','凹陷','硬滑','是'],
['浅白','蜷缩','浊响','清晰','凹陷','硬滑','是'],
['青绿','稍蜷','浊响','清晰','稍凹','软粘','是'],
['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','是'],
['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','是'],
['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','否'],
['青绿','硬挺','清脆','清晰','平坦','软粘','否'],
['浅白','硬挺','清脆','模糊','平坦','硬滑','否'],
['浅白','蜷缩','浊响','模糊','平坦','软粘','否'],
['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','否'],
['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','否'],
['乌黑','稍蜷','浊响','清晰','稍凹','软粘','否'],
['浅白','蜷缩','浊响','模糊','平坦','硬滑','否'],
['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑','否']
]
A = ['色泽','根蒂','敲声','纹理','脐部','触感','好瓜']# 当前样本集合D中第k类样本所占比例为pk(k=1,2,3,…,|y|)
# 计算A的信息熵,以数据最后一列为分类
def getEnt(D):# 获取一个类型k->出现次数的mapkMap = dict()for dLine in D:# 获取分类值kk = dLine[len(dLine) - 1]# 获取当前k出现的次数kNum = kMap.get(k)if kNum is None:kMap[k] = 1else:kMap[k] = kNum + 1# 遍历mapdLen = len(D)rs = 0for kk in kMap:pk = kMap[kk]/dLenrs = rs + pk * math.log2(pk)return -rs# 求信息增益,aIndex为属性列号
def getGain(D,aIndex):dMap = dict()for dLine in D:# 获取属性k = dLine[aIndex]# 属性所属的数组dChildren = dMap.get(k)if dChildren is None:dChildren = []dMap[k] = dChildrendChildren.append(dLine)rs = 0 for key in dMap:dChildren = dMap[key]entx = getEnt(dChildren)print(entx)r = len(dChildren)/len(D) * entxrs = rs + rreturn getEnt(D) - rs
相关文章:

ID3 决策树
西瓜数据集D如下: 编号色泽根蒂敲声纹理脐部触感好瓜1青绿蜷缩浊响清晰凹陷硬滑是2乌黑蜷缩沉闷清晰凹陷硬滑是3乌黑蜷缩浊响清晰凹陷硬滑是4青绿蜷缩沉闷清晰凹陷硬滑是5浅白蜷缩浊响清晰凹陷硬滑是6青绿稍蜷浊响清晰稍凹软粘是7乌黑稍蜷浊响稍糊稍凹软粘是8乌黑稍蜷浊响清晰…...

简单线性回归:预测事物间简单关系的利器
文章目录 🍀简介🍀什么是简单线性回归?🍀简单线性回归的应用场景使用步骤:注意事项: 🍀代码演示🍀结论 🍀简介 在数据科学领域,线性回归是一种基本而强大的统…...
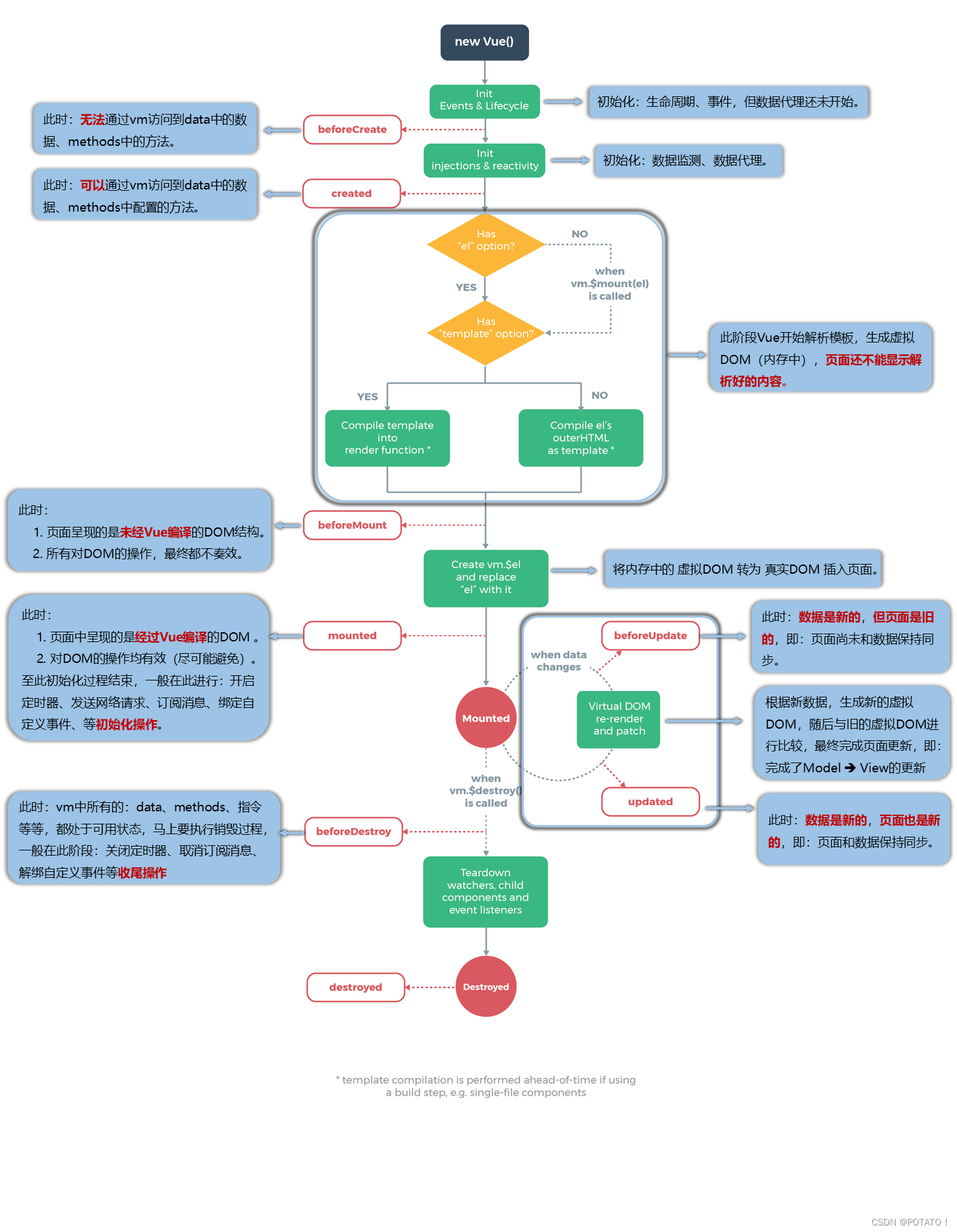
Vue2-收集表单数据、过滤器、内置指令与自定义指令、Vue生命周期
🥔:我徒越万重山 千帆过 万木自逢春 更多Vue知识请点击——Vue.js VUE2-Day4 收集表单数据1、不同标签的value属性2、v-model的三个修饰符 过滤器内置指令与自定义指令1、内置指令2、自定义指令定义语法(1)函数式(2&am…...

正则表达式学习详解
正则表达式 正则表达式(Regular Expression),通常简称为正则或正则表达式,是一种用于描述字符串模式的工具。它是由一系列字符和特殊字符组成的字符串,用于定义搜索模式或进行字符串匹配、替换、提取等操作。 正则表…...
)
工具箱:在线免费使用的文档工具:(PDF转换,图片压缩等)
这些都是博主亲自使用过的,可以使用。 PDF转换器: http://www.pdfdo.com/ 图片压缩: 免费在线图片/视频压缩工具 | 图片压缩 | 免费 JPG PNG GIF 图像压缩 (yalijuda.com) 文档OCR转EXCEL: 文字识别 OCR_ 图片文字识别_图片文字智能识别…...
Qt6之QStackedWidget——Qt仿ToDesk(2)
一、 QStackedWidget概述 QStackedWidget也叫堆栈窗体类,它继承于QFrame,主要与QListWidget等结合使用,实现“一个界面多个页面切换”。 二、QStackedWidget示例 如下图,当点击左边 QListWidget里的菜单时,右边跟随切…...
Harbor企业镜像仓库部署(本地)
简述: Docker 官方镜像仓库是用于管理公共镜像的地方,大家可以在上面找到想要的镜像,也可以把自己的镜像推送上去。但是有时候服务器无法访问互联网,或者不希望将自己的镜像放到互联网上,那么就需要用到 Docker Regis…...

【Linux】如何打包成动静态库,第三方动静态库如何使用?
文章目录 1. 打包成静态库2. 打包成动态库(共享库)3. 使用第三方静态库4. 使用第三方动态库 5. 动态库的加载6. 注意事项 库的名称:去掉前面的 lib 去掉后面的 .a(版本号) .so(版本号) 剩下的,才是库正真的名称。 查看文件依赖库…...

SAP MM学习笔记20- SAP中的英文2 - SD中英文,日语,中文
SD模块中的英文,日语,中文 对照。 販売管理 日本語英語中国語受注伝票sales order销售订单出荷伝票delivery order交货订单ピッキングリストpicking list领货清单シップメント伝票shipment document发运单据出庫確認post goods issue发货确认請求伝票b…...

计算机网络中的一些基本概念
IP地址: 址用于定位主机的网络地址。是一个32位的二进制数,通常被分割为4个“8位二进制数”(也就是4个字节).**端口号:**在网络通信中,IP地址用于标识主机网络地址,端口号可以标识主机中发送数据、接收数据的进程。简单…...

pytest 用例运行方式
一、命令行方式运行 执行某个目录下所有的用例,符合规范的所有用例 进入到对应的目录,直接执行pytest; 例如需要执行testcases 下的所有用例; 可以进入testcases 目录; 然后执行pytest 进入对应目录的上级目录,执行pytest 目录名称/ ; ; 例如需要执行testcases 下…...

简单入门seleniumUI自动化测试
目录 一、selenium的介绍 二、selenium的原理 三、selenium的八种元素定位的方法 1、ID定位: 2 、name定位: 3、class定位: 4、tag定位: 5、link_text定位: 6、partial_link_text定位: 7、css定位…...

Excel(1):表头或列头冻结
1.需求 对于较大的excel,通常需要固定一部分内容,另一份内容为可翻动。 2.解决方式 在视图中选择冻结窗格,需要注意的是,选择冻结窗格时,窗格的左上方的表格区域是固定不动的,只可以向下或者向右活动。...
通达OA SQL注入漏洞【CVE-2023-4166】
通达OA SQL注入漏洞【CVE-2023-4166】 一、产品简介二、漏洞概述三、影响范围四、复现环境POC小龙POC检测工具: 五、修复建议 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损…...
全网最细,Python接口自动化测试-Session会话保持(实战详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 在接口测试的过程…...

Java项目初始化ES、MYSQL表结构及表数据
一、初始化MYSQL数据 public boolean initMysql() throws Exception {log.info("initMysql.start");//获取所连接的数据库名称String database systemMapper.getDatabase();if (StringUtils.isBlank(database)) {throw new BusinessException("连接数据库失败,…...

2023-08-13力扣每日一题
链接: 88. 合并两个有序数组 题意: 如题 解: 从后往前(从大到小)插入排序,这样就不会影响原先的有序性 实际代码: #include<bits/stdc.h> using namespace std; void merge(vector…...
下一代深度学习的思考与若干问题
下一代深度学习的思考和若干问题...

【Linux】IP协议——网络层
目录 IP协议 基本概念 IP协议格式 分片与组装 网段划分 特殊的IP地址 IP地址的数量限制 私网IP地址和公网IP地址 路由 路由表生成算法 IP协议 IP协议全称为“网际互连协议(Internet Protocol)”,IP协议是TCP/IP体系中的网络层协议…...
【CSS学习笔记】
学习内容 1.css是什么 2.CSS怎么用(快速入门) 3.CSS选择器(重点 难点) 4.美化页面(文字、阴影、超链接、列表、渐变…) 5.盒子模型 6.浮动 7.定位 8.网页动画(特效) 1.什么是CSS C…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
