P1123 取数游戏
取数游戏
题目描述
一个 N × M N\times M N×M 的由非负整数构成的数字矩阵,你需要在其中取出若干个数字,使得取出的任意两个数字不相邻(若一个数字在另外一个数字相邻 8 8 8 个格子中的一个即认为这两个数字相邻),求取出数字和最大是多少。
输入格式
第一行有一个正整数 T T T,表示了有 T T T 组数据。
对于每一组数据,第一行有两个正整数 N N N 和 M M M,表示了数字矩阵为 N N N 行 M M M 列。
接下来 N N N 行,每行 M M M 个非负整数,描述了这个数字矩阵。
输出格式
共 T T T 行,每行一个非负整数,输出所求得的答案。
样例 #1
样例输入 #1
3
4 4
67 75 63 10
29 29 92 14
21 68 71 56
8 67 91 25
2 3
87 70 85
10 3 17
3 3
1 1 1
1 99 1
1 1 1
样例输出 #1
271
172
99
提示
样例解释
对于第一组数据,取数方式如下:
[ 67 ] 75 63 10 29 29 [ 92 ] 14 [ 21 ] 68 71 56 8 67 [ 91 ] 25 \begin{matrix} [67] & 75 & 63 & 10 \\ 29 & 29 & [92] & 14 \\ [21] & 68 & 71 & 56 \\ 8 & 67 & [91] & 25 \\ \end{matrix} [67]29[21]87529686763[92]71[91]10145625
数据范围及约定
- 对于 20 % 20\% 20%的数据, 1 ≤ N , ≤ 3 1\le N, \le 3 1≤N,≤3;
- 对于 40 % 40\% 40%的数据, 1 ≤ N , M ≤ 4 1\le N,M\le 4 1≤N,M≤4;
- 对于 60 % 60\% 60%的数据, 1 ≤ N , ≤ 5 1\le N, \le 5 1≤N,≤5;
- 对于 100 % 100\% 100%的数据, 1 ≤ N , M ≤ 6 1\le N, M\le 6 1≤N,M≤6, 1 ≤ T ≤ 20 1\le T\le 20 1≤T≤20。
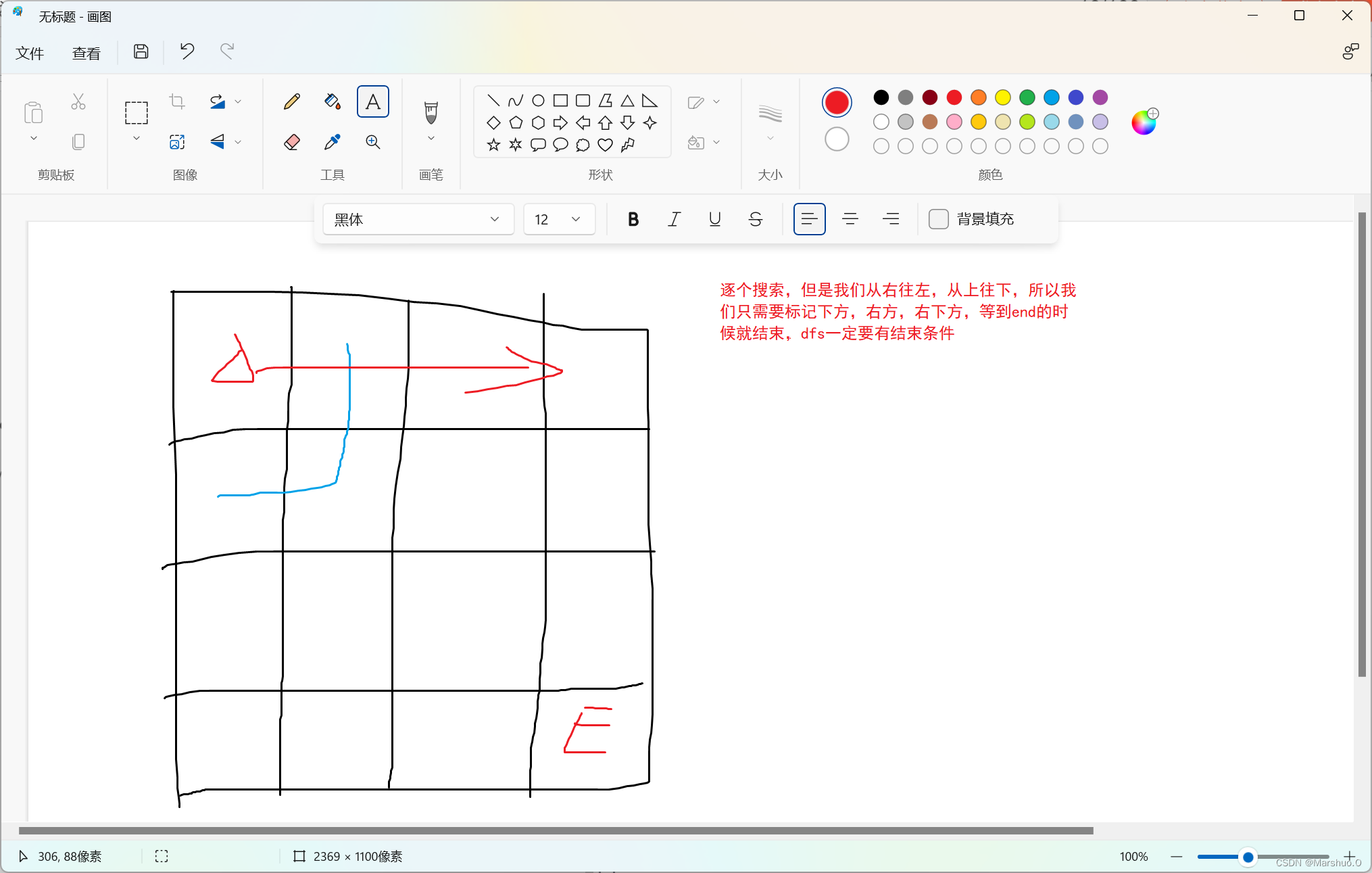
#include<bits/stdc++.h>
using namespace std;
int t,n,m,ans,maxn;
int a[37];
int vis[7][7];
void dfs(int x)
{if(x>=m*n){maxn=max(maxn,ans);return ;}dfs(x+1);if(vis[x/m+1][x%m+1]==0){ans+=a[x];for(int i=x/m;i<=x/m+2;i++){for(int j=x%m;j<=x%m+2;j++)vis[i][j]++;}dfs(x+1);ans-=a[x];for(int i=x/m;i<=x/m+2;i++){for(int j=x%m;j<=x%m+2;j++)vis[i][j]--;}}
}
int main()
{cin>>t;while(t--){cin>>n>>m;for(int i=0;i<n*m;i++)cin>>a[i];memset(vis,0,sizeof vis);dfs(0);cout<<maxn<<endl;maxn=0,ans=0;memset(a,0,sizeof a);}return 0;
}相关文章:

P1123 取数游戏
取数游戏 题目描述 一个 N M N\times M NM 的由非负整数构成的数字矩阵,你需要在其中取出若干个数字,使得取出的任意两个数字不相邻(若一个数字在另外一个数字相邻 8 8 8 个格子中的一个即认为这两个数字相邻),求…...

JavaScript高级:原型与原型链继承方式
在 JavaScript 中,继承是一种重要的概念,它使得对象可以从其他对象继承属性和方法,实现代码的重用和扩展。原型与原型链是 JavaScript 中实现继承的核心机制,虽然听起来有些高深,但我们可以通过通俗易懂的方式来理解它…...
使用vue-grid-layout时 You may need an appropriate loader to handle this file type.
使用vue-grid-layout时 You may need an appropriate loader to handle this file type. node版本不匹配 我的node v14.16.0 vue-gride-layout 需要用 v 2.3.7的版本 卸载后重新安装即可...

C# 2048小游戏核心算法
文章目录 01.程序结构划分02.去零03.合并04.上移05.下移/左移/右移,只是取数据的方向不同06.提高可读性 01.程序结构划分 02.去零 有序向量“唯一化”的思路。 /// <summary>/// 去零/// </summary>/// <param name"row">对于一行或一…...

设计模式(5)代理模式
一、介绍: 【Subject/抽象角色】定义了RealSubject和Proxy的共用接口,这样就可以在任何使用RealSubject的地方都可以使用Proxy 【RealSubject/真实角色】定义Proxy所代表的真实实体 【Proxy/代理角色】保存一个引用使得代理可以访问实体,并…...
Django配置(部署环境较乱,暂时启用)
django配置 web服务器中部署项目及WSGI简介 web服务器 WSGI 在IIS中部署django项目 安装 wfastcgi :pip install wfastcgi安装IIS: 以上选择项勾选后确定 将CGI文件复制到项目中, 将项目复制到IIS默认目录中 部署IIS 添加变量信息如下…...
【设计模式】桥接模式
桥接(Bridge)是用于把抽象化与实现化解耦,使得二者可以独立变化。这种类型的设计模式属于结构型模式,它通过提供抽象化和实现化之间的桥接结构,来实现二者的解耦。 这种模式涉及到一个作为桥接的接口,使得…...

ol问题总结二
一、加载坐标系是4326格式的,使用wfsServer发布的服务,图层加载失败;坐标系是3857格式的。图层加载正常 原因:4326格式的,发布出来的,经纬度是颠倒的 解决方案一:将经纬度进行反转 <templa…...

批量打印-----jsPDF将图片转为pdf,并合并pdf
安装依赖并引入 import jsPDF from jspdf; import { PDFDocument, } from pdf-lib;注意一、 使用jspdf将图片(jpg/jpeg/png/bmp)转pdf(记为pdfA),得到的pdf(pdfA)和需要合并的pdf(记为pdfB)类…...
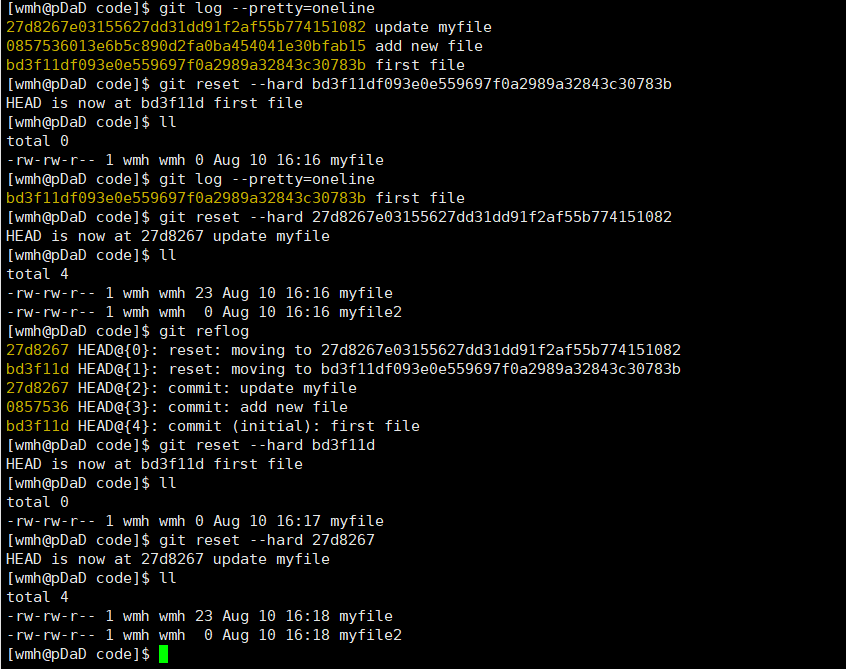
【Git】版本控制器详解之git的概念和基本使用
版本控制器git 初始Gitgit的安装git的基本使用初始化本地仓库配置本地仓库三区协作添加---add修改文件--status|diff版本回退--reset撤销修改删除文件 初始Git 为了能够更⽅便我们管理不同版本的⽂件,便有了版本控制器。所谓的版本控制器,就是⼀个可以记…...
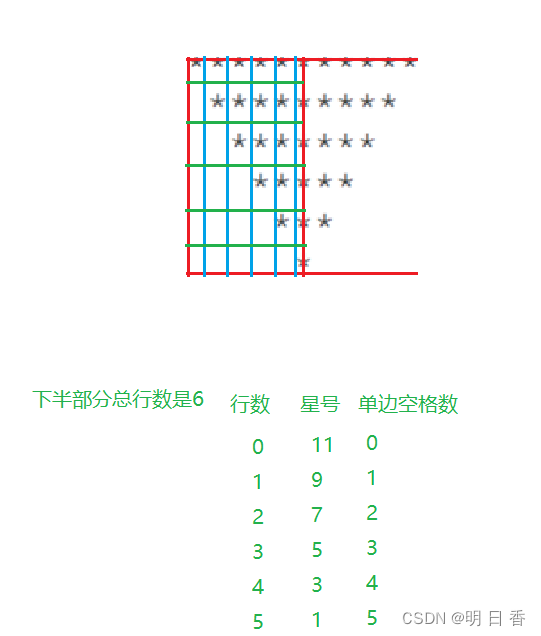
C语言 棱形图案
目录 一、问题分析 上部分: 下部分: 二、代码演示 一、问题分析 如上图所示,我们可以将棱形进行拆解,分为上下两个部分。 上部分: 通过观察,我们得到 单边空格数 上半部分总行数 - 行数 - 1 …...

在idea使用GitHub账号、Copilot异常
登录GitHub显示这样的信息: Invalid authentication data.Connection refused: connect Failed to initiate the GitHub login process. Please try again. 修改hosts(C:\Windows\System32\drivers\etc\hosts),添加以下参数即可…...

面试热题(反转字符串中的单词)
给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。 注意:输入字符串 s中可能会存在前导空格、尾随空格…...

Stable Diffusion WebUI 从零基础到入门
本文主要介绍Stable Diffusion WebUI的实际操作方法,涵盖prompt推导、lora模型、vae模型和controlNet应用等内容,并给出了可操作的文生图、图生图实战示例。适合对Stable Diffusion感兴趣,但又对Stable Diffusion WebUI使用感到困惑的同学&am…...
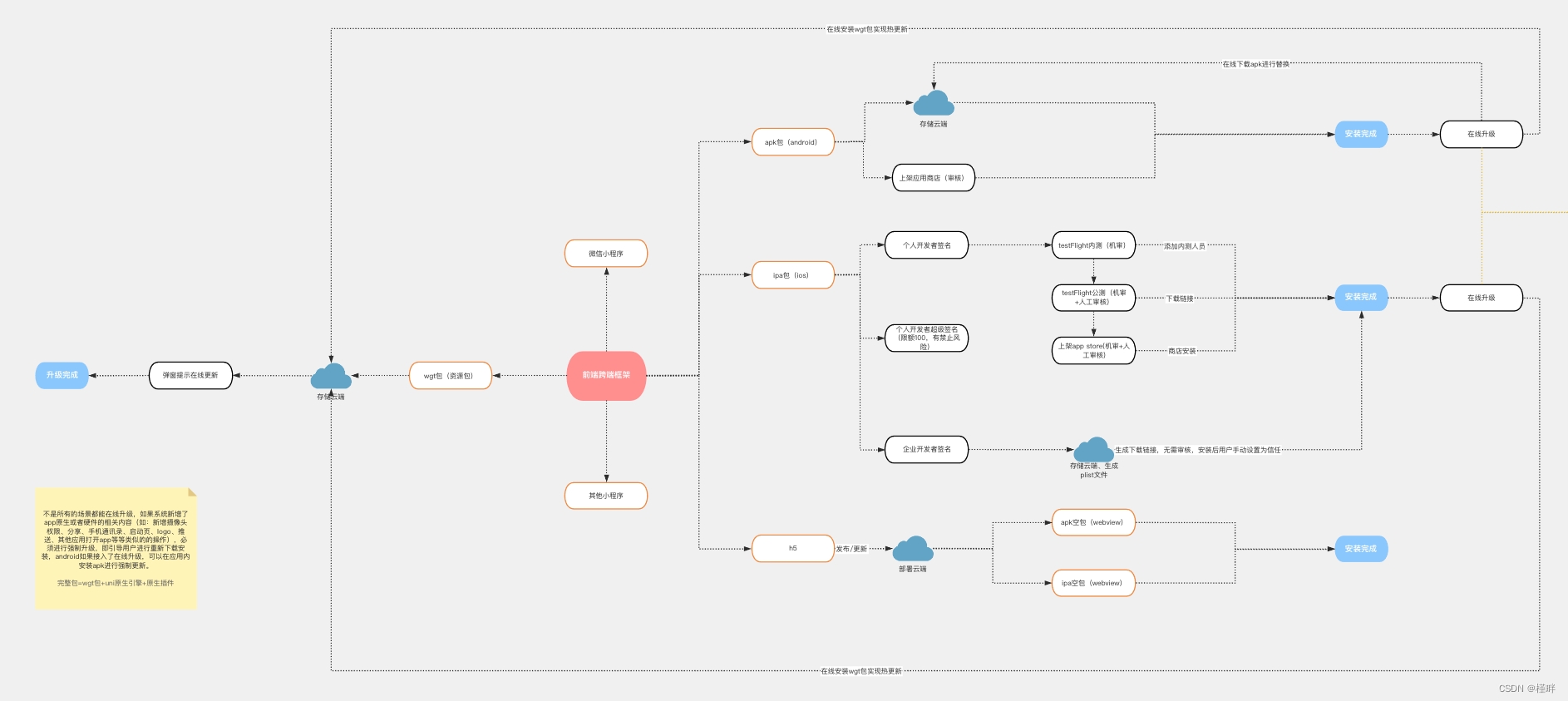
【uniapp】一文读懂app端安装包升级
一、前言 首先,在app端开发上线的过程中,会面临一个问题,就是关于app端的版本升级的问题。如果不做相关处理来引导用户的话,那么app就会出现版本没有更新出现的各种问题,我们常见的有在线升级和去指定地址下载安装两种…...

【算法题】2518. 好分区的数目
题目: 给你一个正整数数组 nums 和一个整数 k 。 分区 的定义是:将数组划分成两个有序的 组 ,并满足每个元素 恰好 存在于 某一个 组中。如果分区中每个组的元素和都大于等于 k ,则认为分区是一个好分区。 返回 不同 的好分区的…...

编写守护进程
守护进程是一个后台进程,当操作系统启动时就可以运行的进程,当操作系统结束时结束的进程,与终端无关。 结果 不想要了就杀死...

stable-diffusion-webui启动No Python at ‘C:\xxx\xxx\python.exe‘
打开webui.bat 把 if not defined VENV_DIR (set "VENV_DIR%~dp0%venv") 中的%~dp0venv改成自己python的安装路径就行获取直接set值即可 如 set VENV_DIRD:\Users\xxx\AppData\Local\Programs\Python\Python310 另外就是直接运行webui-user.bat也可以 如果运行…...
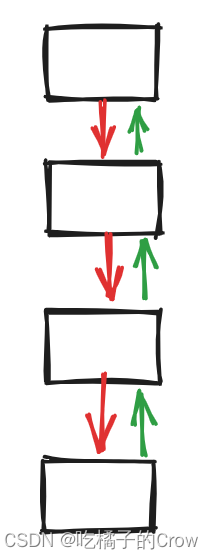
面试热题(合并两个有序列表)
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 合并链表这类型题也是比较经典的题了,因为链表是由指针相互指向而确定位置,所以我们只需要改变某些节点的指针便可以做到对链表进行排序 今天这个方法…...
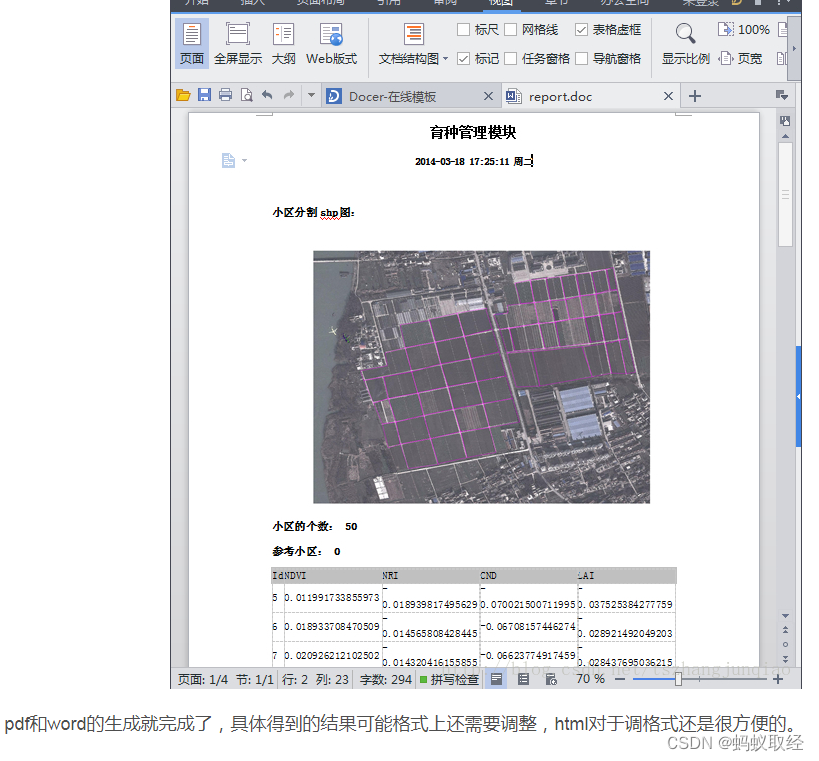
QT生成Word PDF文档
需求:将软件处理的结果保存为一个报告文档,文档中包含表格、图片、文字,格式为word的.doc和.pdf。生成word是为了便于用户编辑。 开发环境:qt4.8.4vs2010 在qt的官网上对于pdf的操作介绍如下:http://qt-project.org/…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...
