论文阅读_AlphaGo_Zero
论文信息
name_en: Mastering the game of Go without human knowledge
name_ch: 在没有人类知识的情况下掌握围棋游戏
paper_addr: http://www.nature.com/articles/nature24270
doi: 10.1038/nature24270
date_publish: 2017-10-01
tags: [‘深度学习’,‘强化学习’]
if: 69.504 Q1 B1 Top
journal: Nature
author: David Silver
zotero id: 8Z2VCLXT
citation: 8443
读后感
AlphaGo Zero是AlphaGo的改进版本,之前版本都使用有监督学习和强化学习相结合的方式。如题——它与之前版本不同的是不需要通过学习人类棋手的下法,其Zero 意思是无师自通。其核心算法是将价值网络和策略网络二合一,并在卷积网络中加入残差。
介绍
文章分两部分,第一部分介绍其整体,第二部分展示了算法细节和一些背景知识(在参考资料之后)。
AlphaGo 是深度强化学习的精典应用范例,围棋领域之所以复杂是因为:在广阔的搜索空间中,需要有精确而精细的前瞻性。
AlphaGo的第一个版本,简称AlphaGo Fun,指2015年战胜樊麾的版本;它使用两个神经网络:价值网络和策略网络。其中的策略网络一开始通过专家数据有监督训练,后期利用强化学习细化;价值网络通过策略网络自我对弈得到数据,从中采样训练;通过蒙特卡洛树搜索(MCTS),价值网络用于计算树中节点的价值,策略网络用于计算最高价值的策略。Alpha Lee是第二个版本,在2016年战胜了李世石,它相对第一版进行了微调,且具有更大的神经网络,也需要更大算力。Alpha Master 是进一步优化版本。
相对于之前版本,AlphaGo Zero有以下优势:
- 使用自我对弈的强化学习,不需要专家知识
- 只使用了棋盘上的黑白子作为输入特征,没有手工构造特征
- 使用单网络:结合了价值网络和策略网络
- 使用简单的树搜索,而不依赖蒙特卡洛展开(Monte Carlo rollouts)
AlphaGo Zero中的强化学习
设环境状态为s,它包含当前状态和历史数据;p表示策略概率,v是当前状态s最终获胜的概率:
(p,v)=fθ(s)(p,v)=f_\theta(s)(p,v)=fθ(s)
其中f是神经网络,theta是网络参数,它根据当前状态输出策略和价值。Zero还对神经网络结构进行了调整:对卷积层加入了残差块,以实现批量归一化和非线性整流。
在每个状态s,都执行神经网络引导下的MCTS搜索,输出是每一种走法的概率π,它先于直接使用f网络输出的策略p,也就是说MCTS改进了神经网络输出的策略。自我对弈后是否胜利又可作为更强的策略评估。训练的目标包含两个:能更准确地评估p和v,且能最终取胜。
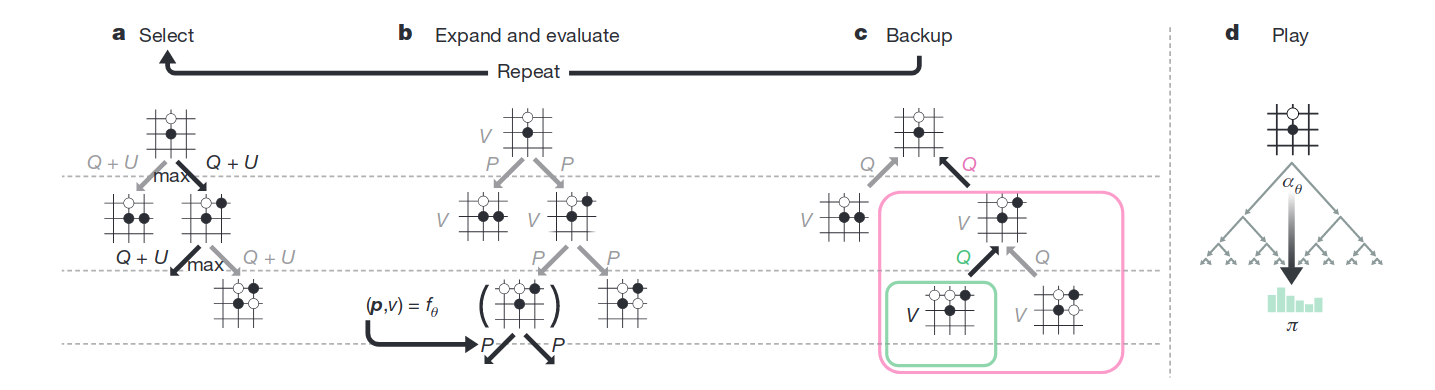
图-2展示了每一次模拟的过程:
- 树中的每个边是其上状态s和选择动作a的组合;
- 每条边都包含:动作的先验概率P(s,a),该边的访问次数N(s,a),动作价值Q(s,a)
- 每一步都选择Q+U最大(上图中子图1),以确认下一步走法,其中U是上置信区间:
U(s,a)∝P(s,a)/(1+N(s,a))U(s, a) ∝ P(s, a) / (1 + N(s, a))U(s,a)∝P(s,a)/(1+N(s,a))
这里的P可视为神经网络f的策略输出(上图中子图2),而引入N是为了平衡探索与利用。当N值小访问次数少时,U更大,以鼓励探索未知领域。
Q计算了下一步可能动作a能到达的状态s’的平均价值(上图中子图3):
Q(s,a)=1/N(s,a)∑s′∣s,a→s′V(s′)Q(s, a)=1 / N(s, a) \sum_{s^{\prime} \mid s, a \rightarrow s^{\prime}} V\left(s^{\prime}\right)Q(s,a)=1/N(s,a)s′∣s,a→s′∑V(s′) - 当搜索完成后,返回搜索概率π
最终公式如下:
(p,v)=fθ(s)and l=(z−v)2−πTlogp+c∥θ∥2(\boldsymbol{p}, v)=f_{\theta}(s) \text { and } l=(z-v)^{2}-\pi^{\mathrm{T}} \log \boldsymbol{p}+c\|\theta\|^{2}(p,v)=fθ(s) and l=(z−v)2−πTlogp+c∥θ∥2
其中l是损失函数。z是实际价值,v是网络输出的价值,p是网络输出的策略概率,π是通过MCTS修正过的策略,c是正则化项,用以约束网络参数,防止过拟合。
训练&分析
在整个训练过程中,共生成了490万次自我对弈,每个MCTS使用1600次模拟,相当于每次移动大约0.4 s的思考时间。
图-3分别对比了,AlphaGo Lee,强化学习 Zero,以及在一开始使用有监督学习的强化学习,随着学习时间增加的模型效果,子图a中Elo rating是用于评价棋手水平;子图b用于预测人类棋手动作;子图c用于预测谁能获胜。
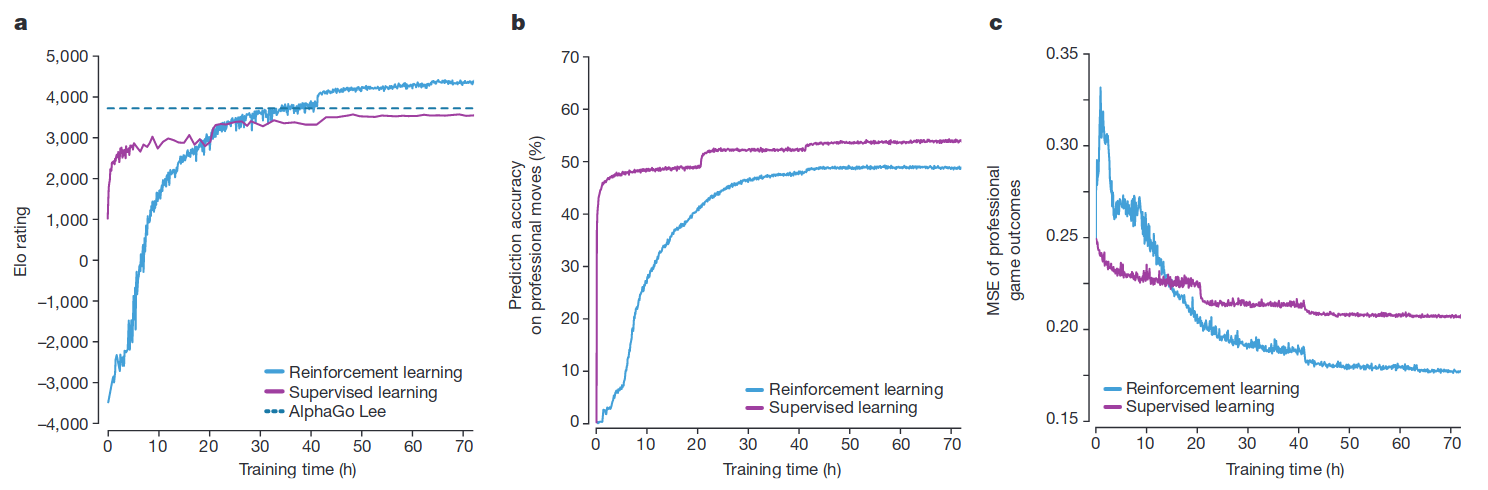
Alpha Zero仅用了36 小时就超过了Alpha Lee,72小时后完胜。相比之下,Alpha Zero使用4个TPU的单机,Alpha Lee分布在多台机器上,经过了几个月的训练。
比较出人意料的是,前期向专家学习反而限制了最终模型的效果;另外,和专家学习能更好地预测人的动作,但不能达到最好的效果,似乎说明学习专家反而抑置机器的表现(不过,我觉得这可能和计算U时的N有关,也是可改进的)。
作者还实验了修改网络结构对模型的影响,发现加入残差层和神经网络二合一分别提升了模型效果。
学到的知识和最终效果
AlphaGo Zero从完全随机的动作迅速发展到对围棋概念的复杂理解,包括引信、战术、生死、ko 、yose、捕获比赛、哨兵、形状、影响和领地……
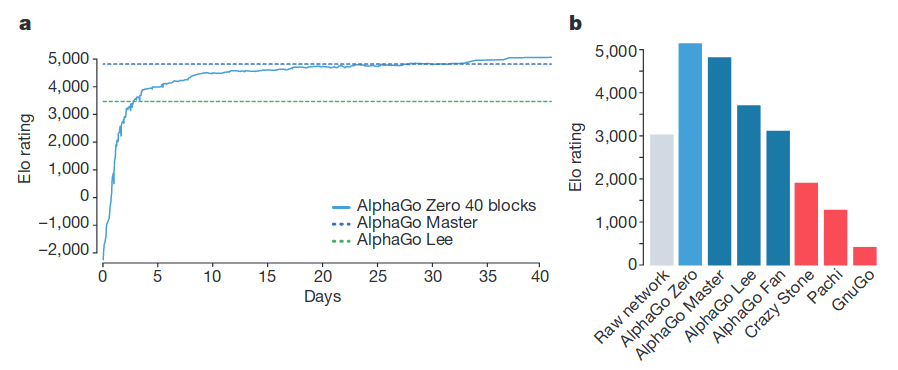
图-6展示了Zero与其它模型的对比效果,Elo rating中200分的差距对应75 %的获胜概率。
相关文章:

论文阅读_AlphaGo_Zero
论文信息 name_en: Mastering the game of Go without human knowledge name_ch: 在没有人类知识的情况下掌握围棋游戏 paper_addr: http://www.nature.com/articles/nature24270 doi: 10.1038/nature24270 date_publish: 2017-10-01 tags: [‘深度学习’,‘强化学习’] if: 6…...

一文教你用Python创建自己的装饰器
python装饰器在平常的python编程中用到的还是很多的,在本篇文章中我们先来介绍一下python中最常使用的staticmethod装饰器的使用。 目录一、staticmethod二、自定义装饰器python类实现装饰器python函数嵌套实现装饰器多个装饰器调用三、带参数的装饰器一、staticmet…...
)
华为OD机试 - 任务总执行时长(JS)
任务总执行时长 题目 任务编排服务负责对任务进行组合调度。参与编排的任务又两种类型,其中一种执行时长为taskA,另一种执行时长为taskB。任务一旦开始执行不能被打断,且任务可连续执行。服务每次可以编排num个任务。 请编写一个方法,生成每次编排后的任务所有可能的总执…...
pytorch离线快速安装
1.pytorch官网查看cuda版本对应的torch和torchvisionde 版本(ncvv -V,nvidia-sim查看cuda对应的版本) 2.离线下载对应版本,网址https://download.pytorch.org/whl/torch_stable.html 我下载的: cu113/torch-1.12.0%2Bcu113-cp37-cp37m-win_…...
)
华为OD机试 - 数组合并(JS)
数组合并 题目 现在有多组整数数组,需要将他们合并成一个新的数组。 合并规则,从每个数组里按顺序取出固定长度的内容合并到新的数组中, 取完的内容会删除掉, 如果该行不足固定长度或者已经为空, 则直接取出剩余部分的内容放到新的数组中,继续下一行。 如样例1,获得长度3,先遍…...

不要让GPT成为你通向“学业作弊”的捷径——使用GPT检测工具来帮助你保持正确的方向
不要让GPT成为你通向“学业作弊”的捷径——使用GPT检测工具来帮助你保持正确的方向 最近,多所美国高校以及香港大学等都明确禁止在校使用ChatGPT等智能文本生成工具。GPT(Generative Pre-trained Transformer)是一种自然语言处理技术&#x…...
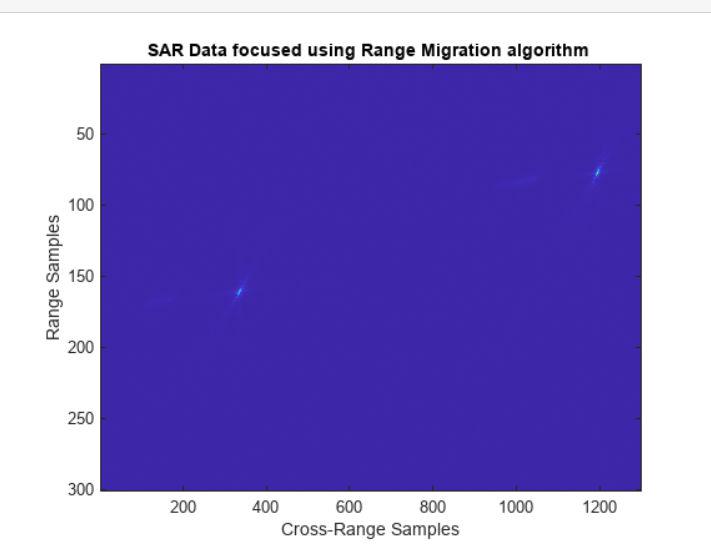
基于matlab的斜视模式下SAR建模
一、前言此示例说明如何使用线性 FM (LFM) 波形对基于聚光灯的合成孔径雷达 (SAR) 系统进行建模。在斜视模式下,SAR平台根据需要从宽侧斜视一定角度向前或向后看。斜视模式有助于对位于当前雷达平台位置前面的区域进行…...

15-基础加强-1-类加载器反射
文章目录1.类加载器1.1类加载器【理解】1.2类加载的过程【理解】1.3类加载的分类【理解】1.4双亲委派模型【理解】1.5ClassLoader 中的两个方法【应用】2.反射2.1反射的概述【理解】2.2获取Class类对象的三种方式【应用】 第1步:获取类的Class对象2.3反射获取构造方…...
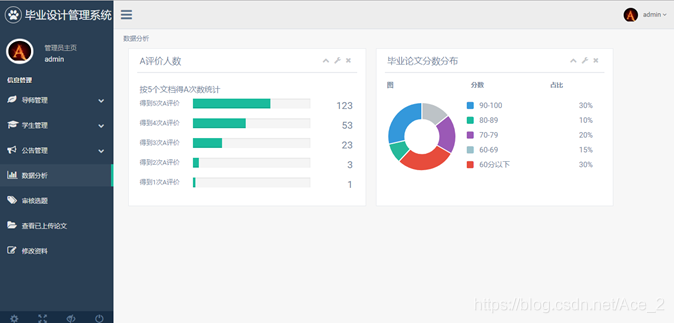
基于SSM,Spring, BootStrap 毕业设计管理系统的设计与实现
目录 一.前言介绍 二、主要技术 2.1 SSM框架介绍 2.2 MYSQL数据库 2.3 持久层框架MyBatis 2.4 前端框架BootStrap 三. 系统设计 3.1 系统架构设计 3.2 系统功能模块 3.2.1 学生模块 3.2.2 教师模块 3.2.3 管理员模块 四、数据库设计 4.1 数据分析 4.2 概念设计 …...

一招鉴别真假ChatGPT,并简要介绍ChatGPT、GPT、GPT2和GPT3模型之间的区别和联系
以下内容除红色字体部分之外,其他均来源于ChatGPT自动撰写。 ChatGPT是基于GPT模型的对话生成模型,旨在通过对话模拟实现自然语言交互。它是为了改善人机对话体验而设计的,主要应用于聊天机器人、智能客服等场景。 与GPT模型相比,…...
)
华为OD机试 - 特异性双端队列(JS)
特异性双端队列 题目 有一个特异性的双端队列,该队列可以从头部到尾部添加数据,但是只能从头部移除数据。 小A一次执行 2n 个指令往队列中添加数据和移除数据, 其中 n 个指令是添加数据(可能从头部也可以从尾部添加) 依次添加 1 到 n , n 个指令是移出数据 现在要求移除数…...

Nginx自动封禁可疑Ip
文章目录一、Nginx封禁ip1、简介2、nignx 禁止IP访问2.1 方法一2.2 方法二3、关于 deny 的使用二、脚本自动封禁Ip1、流程介绍2、脚本实战2.1 核心脚本解释2.2 编写shell脚本2.3 crontab定时一、Nginx封禁ip 1、简介 在网站维护过程中,有时候我们需要对一些IP地址…...
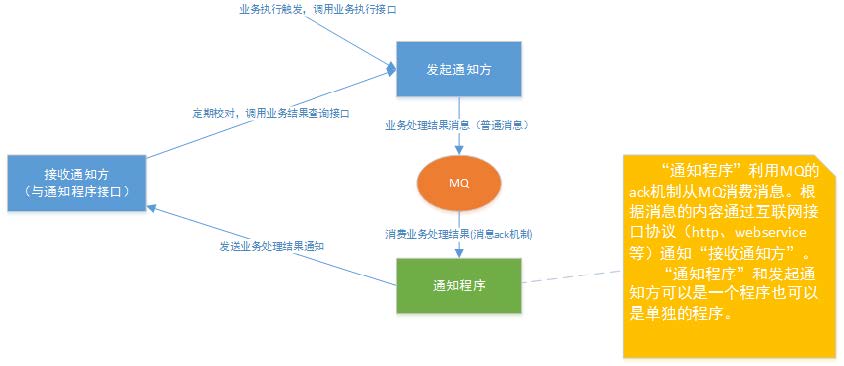
分布式事务--理论基础
1、事务基础 1.1、什么是事务 事务可以看做是一次大的活动,它由不同的小活动组成,这些活动要么全部成功,要么全部失败。 1.2、本地事务 在同一个进程内,控制同一数据源的事务,称为本地事务。例如数据库事务。 在计…...
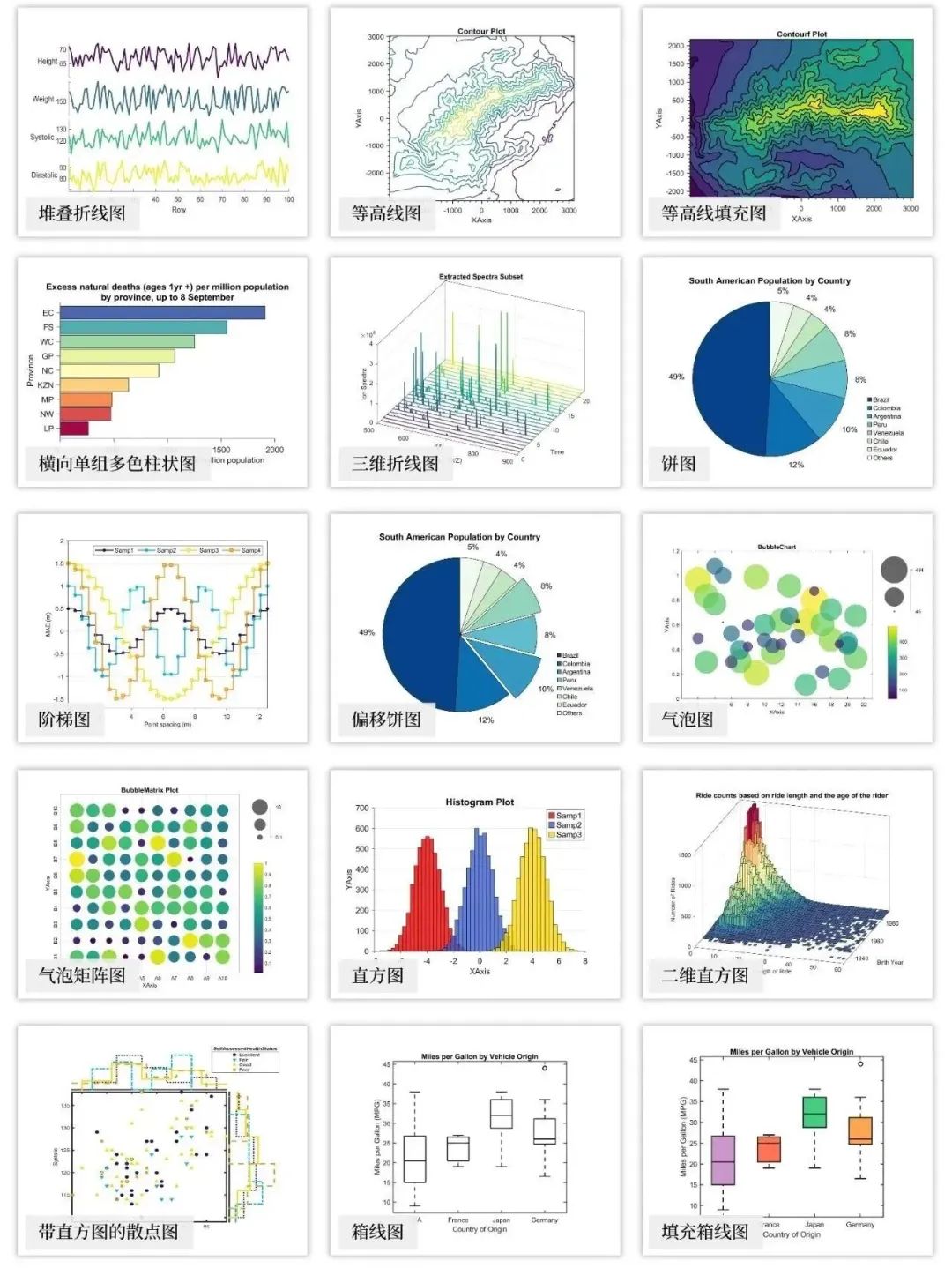
Matlab数学建模常用算法及论文插图绘制模板资源合集
最近有很多朋友咨询我关于Matlab论文插图绘制方面的问题。 问了一下,这些朋友中,除了写博士论文的,大部分都是要参加美赛的。 这让我突然想起,自己曾经为了水论文,购买过一批Matlab数学建模的资料。 想了想…...

C语言【动态内存管理 后篇】
动态内存管理 后篇🫅经典例题🤦♂️题目1🤦♂️题目2🤦♂️题目3🤦♂️题目4🫅C/C程序的内存开辟前面的一篇文章动态内存管理 前篇,我们已经了解过了动态内存管理的相关信息,…...
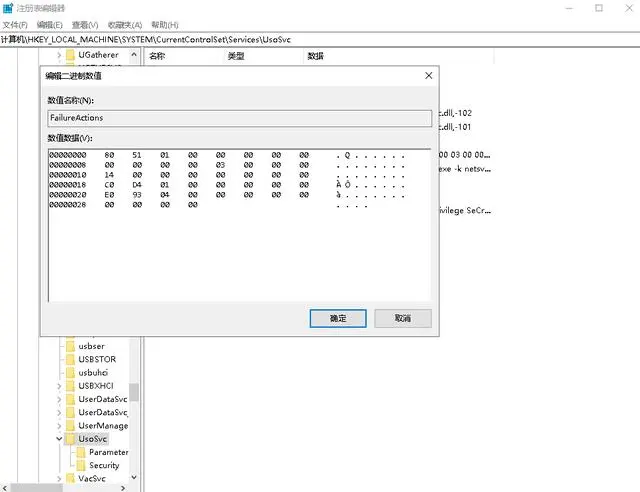
四大步骤,教你彻底关闭Win10自动更新
文章目录一、禁用Windows Update服务二、在组策略里关闭Win10自动更新相关服务三、禁用任务计划里边的Win10自动更新四、在注册表中关闭Win10自动更新参考资料一、禁用Windows Update服务 1、同时按下键盘 Win R,打开运行对话框,然后输入命令 services…...
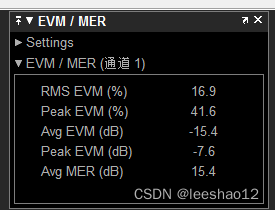
通信算法之一百零四:QPSK完整收发仿真链路
1.发射机物理层基带仿真链路 1.1 % Generates the data to be transmitted [transmittedBin, ~] BitGenerator(); 2.2 % Modulates the bits into QPSK symbols modulatedData QPSKModulator(transmittedBin); 2.3 % Square root Raised Cosine Transmit Filter %comm…...
时间复杂度(超详解+例题)
全文目录引言如何衡量一个算法的好坏时间复杂度时间复杂度的定义时间复杂度的大O表示法实例test1test2test3test4test5总结引言 如何衡量一个算法的好坏 我们在写算法的时候,对于实现同样的作用的不同算法,我们如何判断这个算法的好坏呢? …...

【Java面试总结】Maven篇
【Java面试总结】Maven篇1.Maven坐标是啥2.Maven常见的依赖范围有哪些?3.多模块如何聚合4.对于一个多模块项目,如果管理项目依赖的版本5.maven怎么解决版本冲突6.Maven常用命令有哪些?1.Maven坐标是啥 一般maven使用groupID,artifactId&…...

【每日一题Day123】LC1792最大平均通过率 | 堆
最大平均通过率【LC1792】 一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生&#…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...
