河南工程学院2.17蓝桥杯培训
乘法口诀数列:https://www.acwing.com/problem/content/3466/
剪绳子:https://www.acwing.com/problem/content/68Sin
SinSine之舞:http://lx.lanqiao.cn/problem.page?gpid=D5272
数列:https://www.acwing.com/problem/content/430/
1,乘法口诀
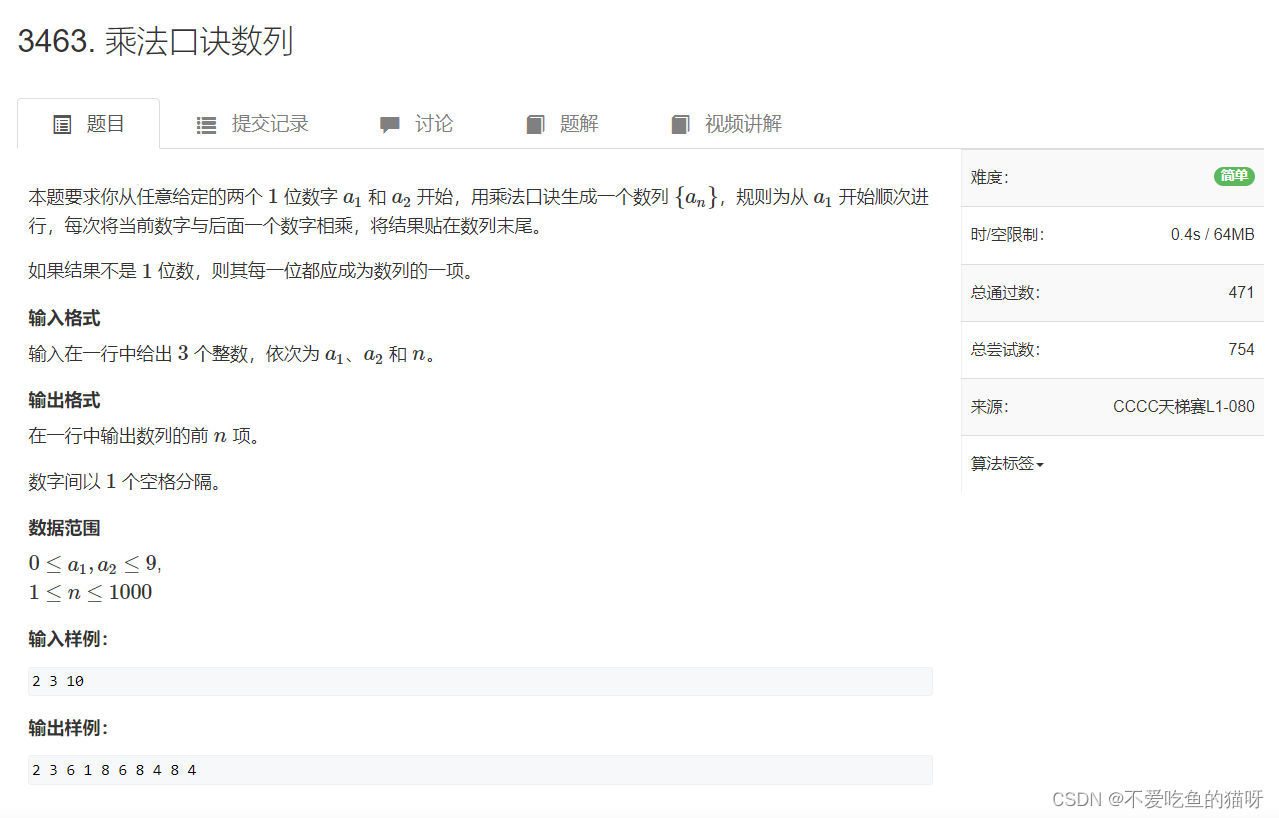
这道题没有多大难度,纯模拟即可
i++ 即后加加,原理是:先自增,然后返回自增之前的值
++i 即前加加,原理是:先自增,然后返回自增之后的值
#include <bits/stdc++.h>
using namespace std;
int m;
int a[1010].
int main(){int a1,a2,ans=0;cin>>a1>>a2>>m;a[0]=a1,a[a2.ans=a1*a2;for(int i=2,j=1;i<m;j++,i++){if(ans<10) a[i]=ans;else{a[i]=ans/10;a[++i]=ans%10;}ans=a[j]*a[j+1];}for(int i=0;i<m;i++)cout<<a[i]<<" ";return 0;
}2,剪绳子
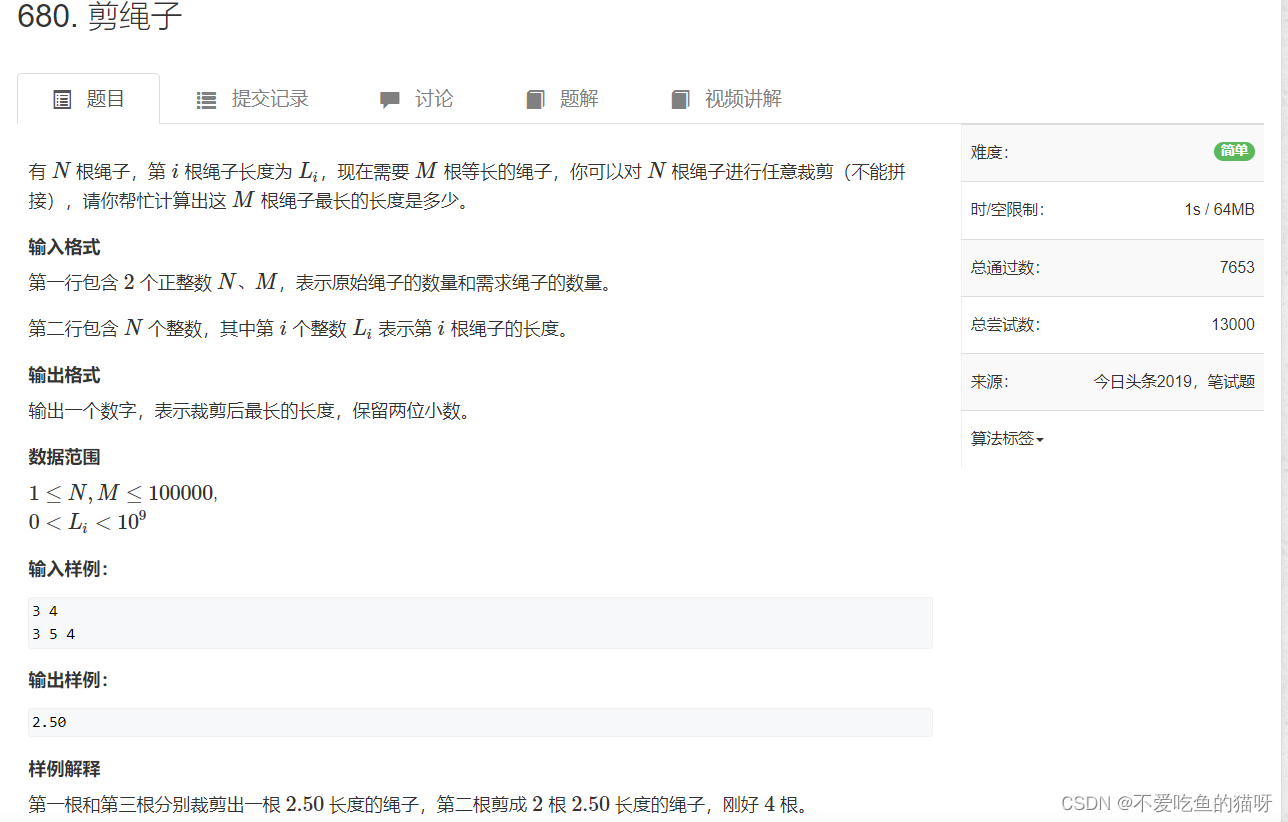
这道题用到的算法是浮点二分,需要找到最优解,但是如果直接做会比较麻烦,但可以用二分寻找答案,可以先设一个满足条件的X(是这道题具有判断性),然后确定是不是最优的
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],n,m;
bool check(double mid){int cnt=0;for(int i=0;i<n;i++){cnt+=a[i]/mid;//向下取整}return cnt>=m;//,满足条件返回true
}
int main(){scanf("%d%d",&n,&m);for(int i=0;i<n;i++)scanf("%d",&a[i]);double l=0.0,r=1e9;while(r-l>1e-4)//最小精度{double mid=(l+r)/2;.//注意与整数二分的区别if(check(mid))l=mid;else r=mid;}printf("%.2lf\n",l);
}3,Sine之舞
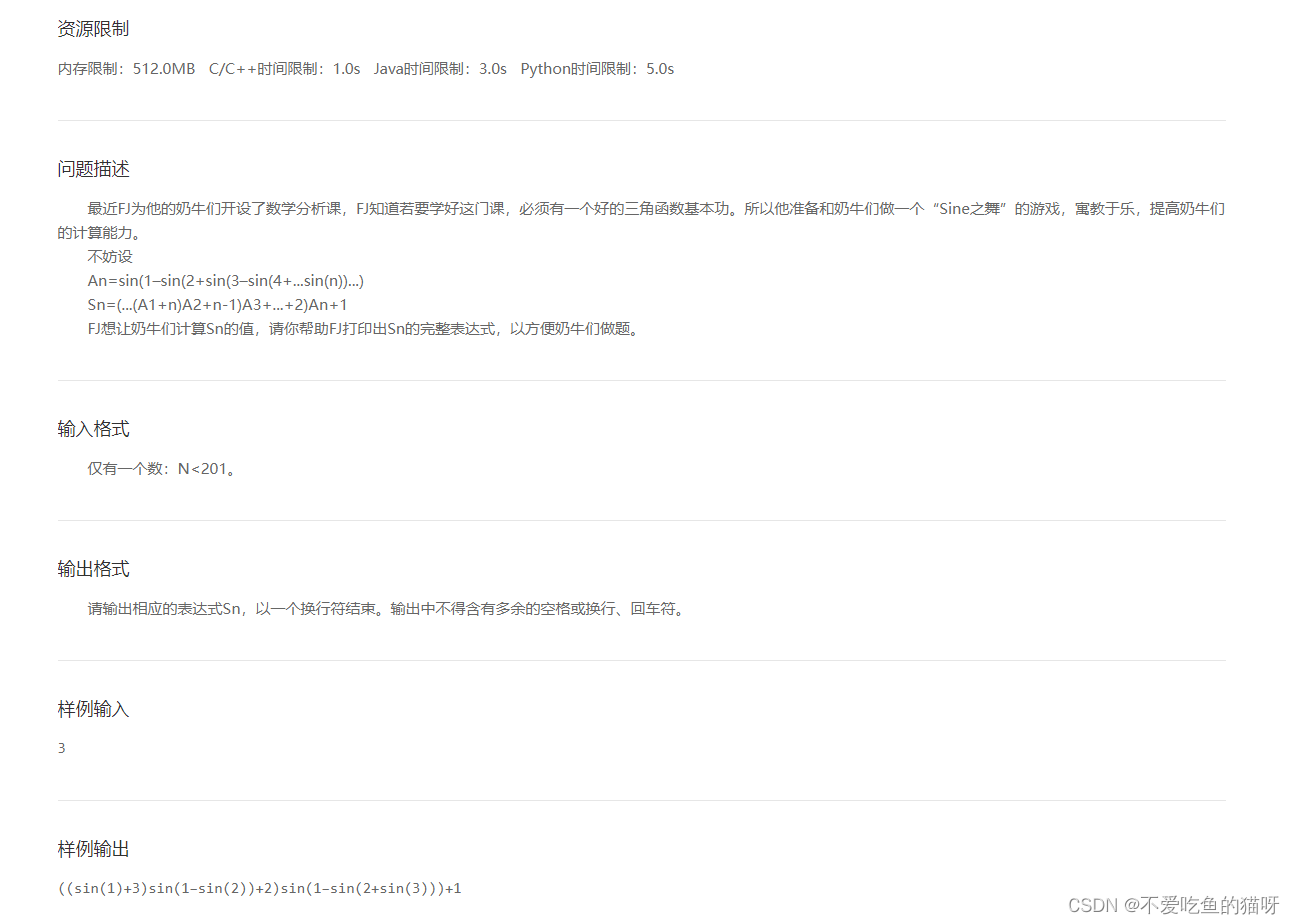
这道题主要考察递归算法和递推思想,是有点难度的,需要确定An,Sn,且Sn递归中包括An递归,
A1=sin(1);
A2=sin(1-sin(2)),
S1=A1+1
S2=(A1+2)A2+1
#include <bits/stdc++.h>
using namespace std;
void An(int i,int n){if(i==1)cout<<"sin("<<i<<")";else{if(i%2==0){cout<<"sin("<<i<<"+";An(i+1,n);cout<<")";}else{cout<<"sin("<<i<<"-";An(i+1,n);cout<<")";}}
}
void Sn(int n,int i){if(n==1){An(1,n);cout<<"+"<<i;}else{cout<<"(";Sn(n-1,i+1);cout<<")";An(1,n);cout<<"+"<<i;}
}
int main()
{int n;cin>>n;Sn(n,1);return 0;
}相关文章:

河南工程学院2.17蓝桥杯培训
乘法口诀数列:https://www.acwing.com/problem/content/3466/ 剪绳子:https://www.acwing.com/problem/content/68Sin SinSine之舞:http://lx.lanqiao.cn/problem.page?gpidD5272 数列:https://www.acwing.com/problem/content/…...

【JavaSE】数据类型与变量
JAVA之父:詹姆斯高斯林 (James Gosling) 前言: 大家好,我是程序猿爱打拳。今天我给大家讲解的是Java基础中的数据类型。主要讲解的是各个类型的应用场景以及注意事项。 目录 1.数据类型 2.常量与变量 2.1常量 2.2变…...

生成模型技术发展过程
生成模型生成模型和判别模型的差异生成模型的目标是在给定了数据集D,并且假设这个数据集的底层分布(underlying distribution)是Pdata,我们希望够近似出这个数据分布。如果我们能够学习到一个好的生成模型,我们就能用这个生成模型为下游任务做…...
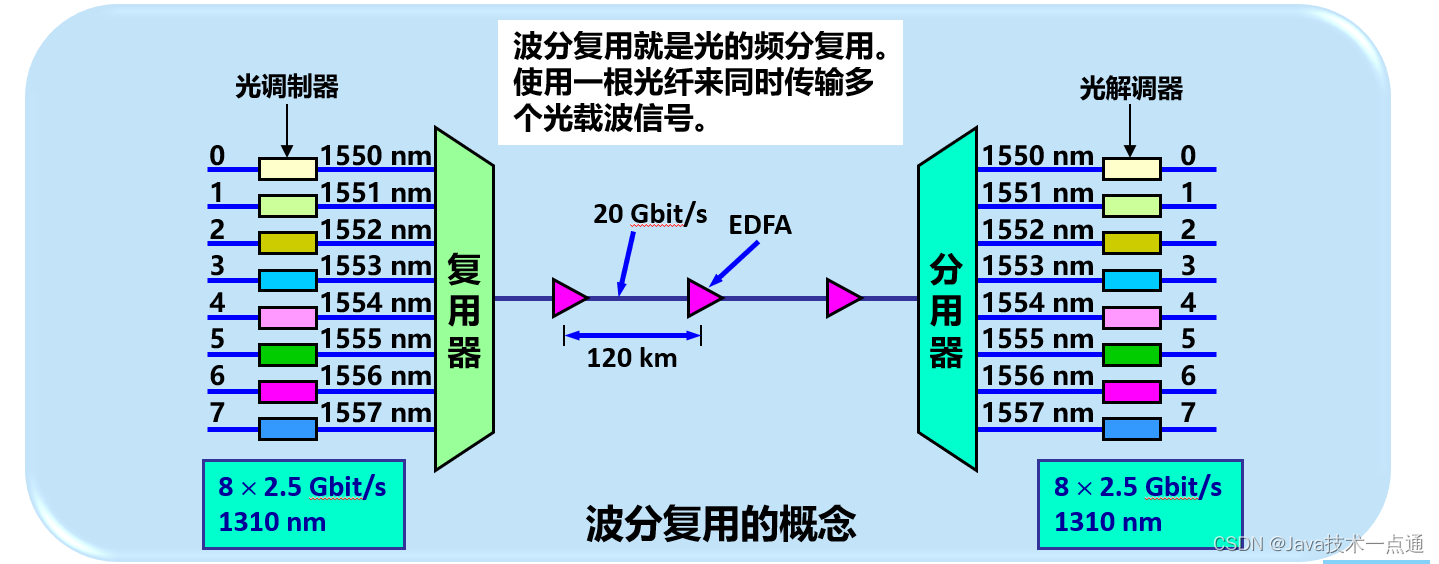
计算机网络第2章(物理层)学习笔记
❤ 作者主页:欢迎来到我的技术博客😎 ❀ 个人介绍:大家好,本人热衷于Java后端开发,欢迎来交流学习哦!( ̄▽ ̄)~* 🍊 如果文章对您有帮助,记得关注、点赞、收藏、…...

4564: 保留尾部*
描述规定输入的字符串中只包含字母和*号,除了尾部的*号之外,请将字符串中其他*号全部删除。输入输入数据包括一串字符串,只包含字母和*,总长度不超过80。输出输出按要求删除*后的字符串。样例输入*******A*BC*DEF*G****样例输出AB…...
安卓项目搭建grpc环境
本篇文章使用的IDE是Android Studio。这里先吐槽一句,安卓项目搭建grpc环境,不管是引入插件还是引入第三方库,对于版本的要求都极为苛刻,一旦版本不匹配就会报错,所以对于版本的搭配一定要注意。 下面介绍的这个版本搭…...
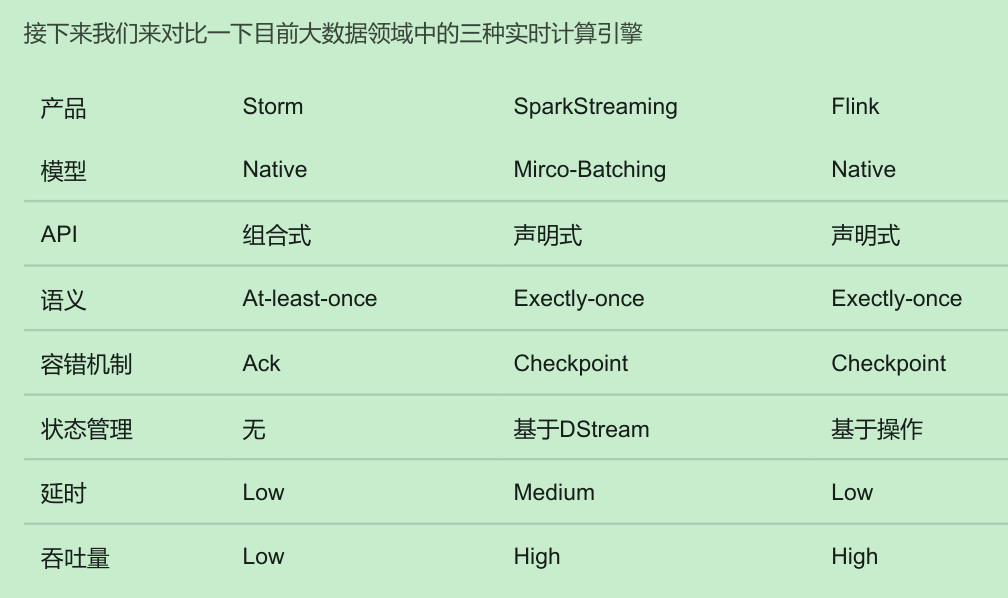
Flink01: 基本介绍
一、什么是Flink 1. Flink是一个开源的分布式,高性能,高可用,准确的流处理框架 (1)分布式:表示flink程序可以运行在很多台机器上, (2)高性能:表示Flink处理性…...

设计模式之单例模式
文章の目录一、什么是单例模式二、如何实现单例模式1、利用JavaScript中的全局对象2、静态成员改造参考写在最后一、什么是单例模式 单例模式也称为单体模式,保证一个类仅有一个实例,并提供一个访问它的全局访问点。 举个栗子:一个班级只有一…...

[oeasy]python0086_ASCII_出现背景_1963年_DEC_PDP系列主机_VT系列终端
编码进化 回忆上次内容 上次 回顾了 字符编码的新陈代谢 ibm 曾经的EBCDIC 由于 字符不连续导致 后续 出现无数问题 随着 网络的发展 数据交换的 需要原来的小隐患现在 产生了 巨大问题 Bemer 联合各方巨头 想要推出 字符连续的编码集 这新编码集 具体长什么样 呢࿱…...
基于FFmpeg实现的无声音屏幕录制
UI自动化测试时,有时需要进行录屏操作,这时我们是不需要声音的,我们可以通过FFmpeg进行简单的录制工作。 以下是在windows10环境下,基于FFmpeg实现的简单录制: Ffmpeg简介: 功能:有非常强大的…...
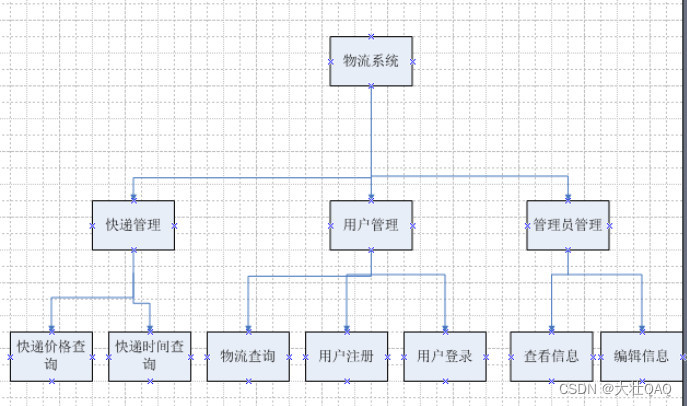
【项目精选】基于JSP物流信息网(论文+源码+视频)
点击下载源码 近年来,随着时代的进步,社会随之不断发展,经济也快速发展起来了,人民的消费水平在不断地提高,平常的实体店消费已经不能满足人们的需求;在者,互联网技术的不断发展也为电子商务的兴…...
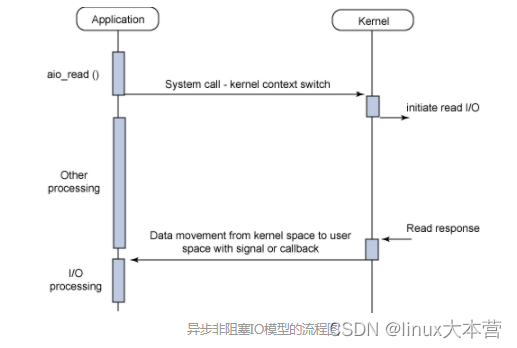
linux异步IO编程实例分析
在Direct IO模式下,异步是非常有必要的(因为绕过了pagecache,直接和磁盘交互)。linux Native AIO正是基于这种场景设计的,具体的介绍见:KernelAsynchronousI/O (AIO)SupportforLinux。下面我们就来分析一下…...
)
日常英语口语练习-情景交际场景25(三)
登山踏青m: hey Carol, what are you doing this weekend?o: im going hiking /haikiŋ/登山with my husband and our hiking clubm: you have a hiking culb?o: yes, we do, we have 30 to 40 people of all ages and skill levelsm: thats great, do you gus do…...

Qt 工程师进阶技术23种设计模式
Qt 工程师进阶技术23种设计模式【1】23种设计模式【1】23种设计模式 设计模式是解决特定问题的一系列套路,这套方案提高代码可复用性、可读性、稳健性、可维护性及安全性。 23种设计模式可分为三类:结构型模式(侧重类与对象之间的组合)、行为型模式(侧重…...
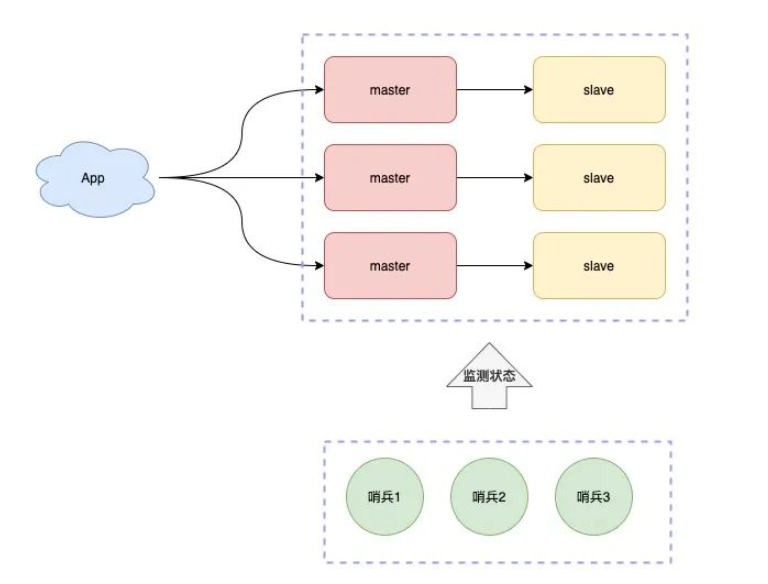
Redis 强化
(Redis入门使用查看)https://blog.csdn.net/weixin_73849581/article/details/128390152?spm1001.2014.3001.5501缓存使用原则什么时候,什么样的数据能够保存在Redis中?1.数据量不能太大2.使用越频繁,Redis保存这个数据越值得3.保存在Redis中的数据一般不会是数据库中频繁修改…...
)
华为OD机试题 - 众数和中位数(JavaScript)
最近更新的博客 华为OD机试题 - 任务总执行时长(JavaScript) 华为OD机试题 - 开放日活动(JavaScript) 华为OD机试 - 最近的点 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试题 - 最小步骤数(JavaScript) 华为OD机试题 - 任务混部(JavaScript) 华为OD机试题 - N 进…...

Go: expected pseudo-register found R13 error
报错描述: 启动Go项目时,报错: ../../../.go/pkg/mod/github.com/choleraehyq/pidv0.0.10/pid_go1.5_amd64.s:28: expected pseudo-register; found R13 原因分析: github.com/choleraehyq/pid这个依赖包的版本太低,需…...
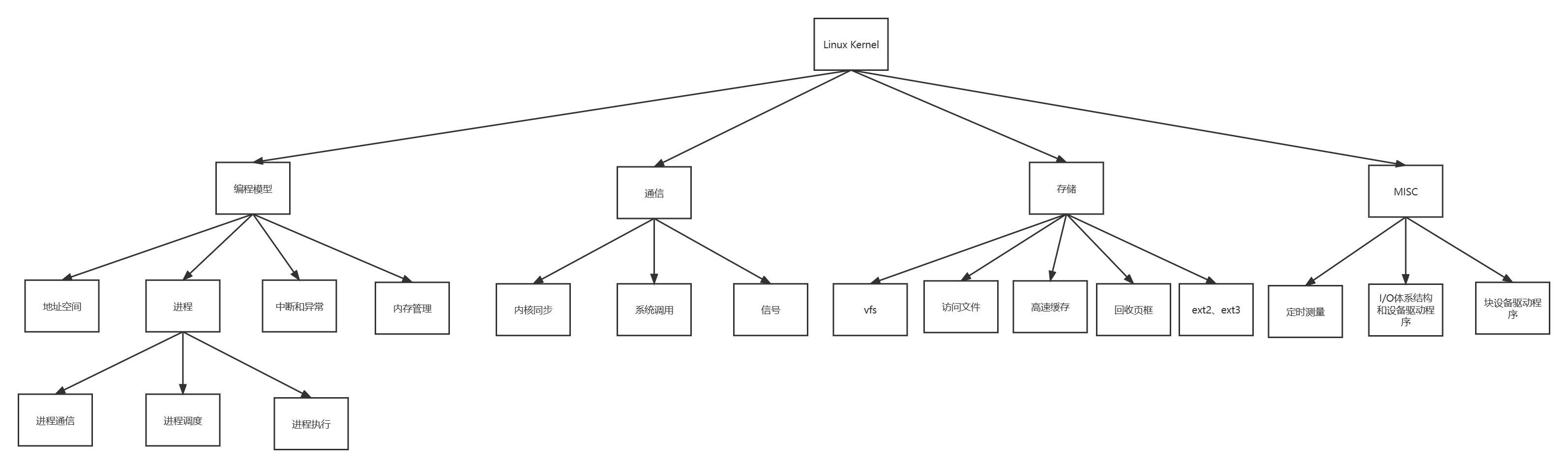
程序员必备的技能-深入理解 Linux 内核拆解
841 页的《深入理解 Linux内核》堪称经典,时隔多年打开,泛黄的纸张上面仍然跳跃出一个个让人心潮澎湃的知识点,突然让我想起一位微信朋友的昵称:知识的舔狗!拆,开始~前言第一章 绪论Linux与其他类Unix内核…...
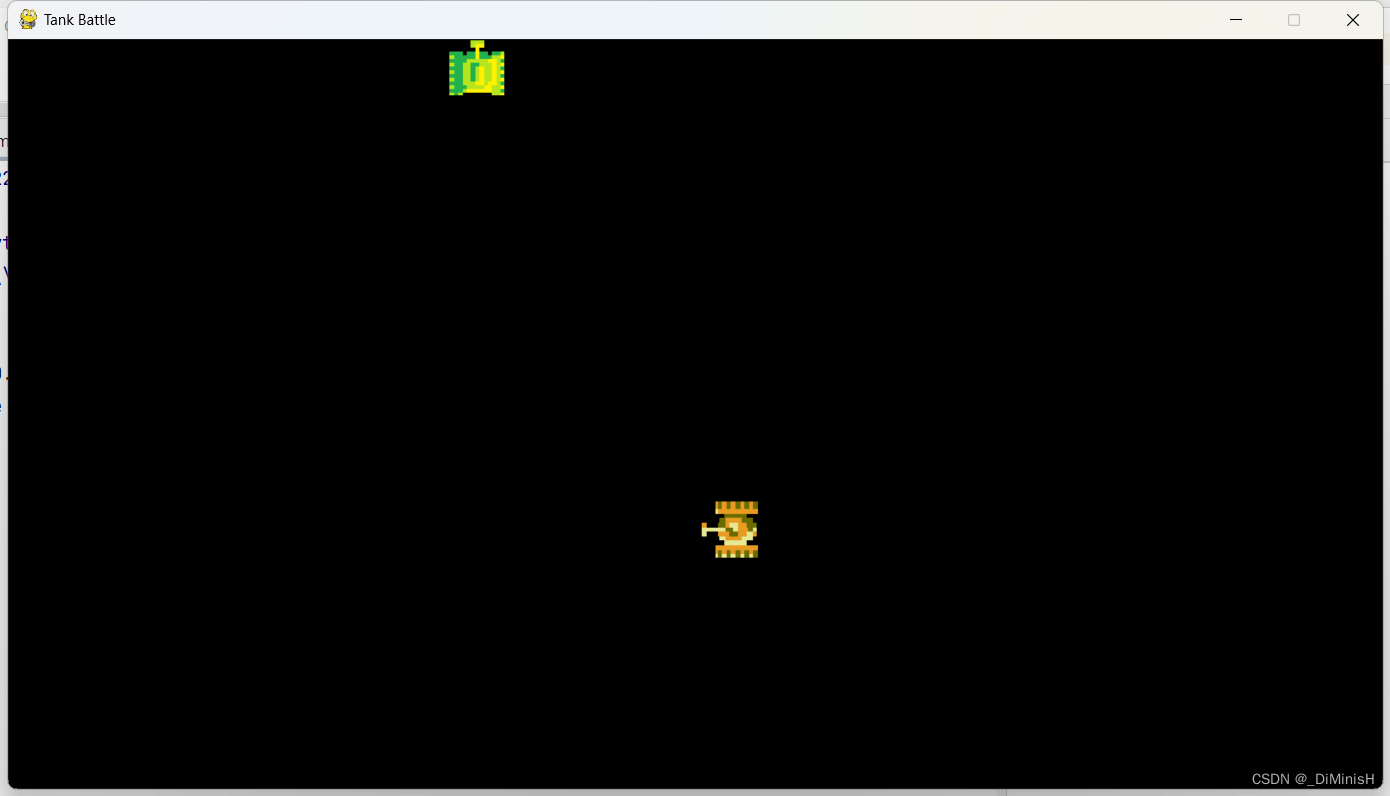
学习 Python 之 Pygame 开发坦克大战(三)
学习 Python 之 Pygame 开发坦克大战(三)坦克大战物体碰撞检测编写1. 实现敌方坦克与我方坦克间的碰撞2. 实现敌方坦克间的碰撞3. 实现玩家子弹与敌方坦克间的碰撞4. 实现敌方子弹与我方坦克间的碰撞 和 玩家复活5. 爆炸效果类6. 为子弹爆炸添加爆炸效果…...
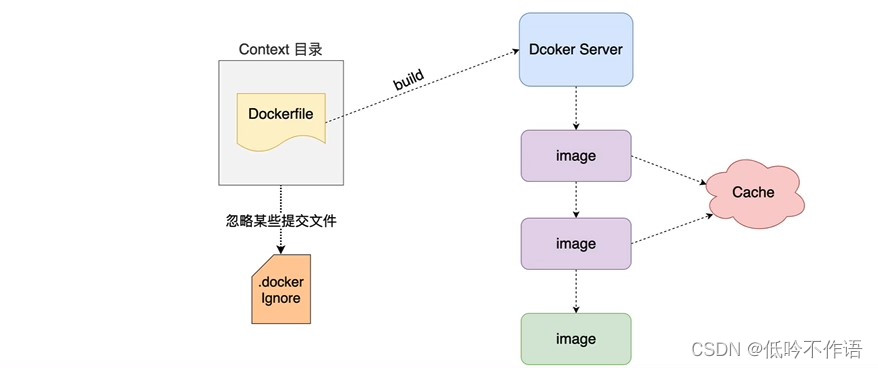
Docker 学习笔记
概述 1. 什么是 Docker? Docker 是一个应用容器平台,管理项目中用到的所有环境(MySQL、Redis…) 2. Docker 和虚拟机的区别 虚拟机是携带操作系统的,本身很小的应用程序因为携带了操作系统而变得十分笨重࿰…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
