途乐证券-KDJ分别代表什么?
 KDJ是一种技能剖析东西,常见于股票、期货等商场中,它的全称是随机目标(KDJ)。KDJ目标包括三条线,分别为K线、D线和J线。那么,KDJ分别代表什么呢?本文将从多个视点进行剖析。
KDJ是一种技能剖析东西,常见于股票、期货等商场中,它的全称是随机目标(KDJ)。KDJ目标包括三条线,分别为K线、D线和J线。那么,KDJ分别代表什么呢?本文将从多个视点进行剖析。
1. KDJ的简单介绍
KDJ目标的计算公式如下:
RSV=(收盘价-最低价)÷(最高价-最低价)×100
其间,最近n个交易日的最高价和最低价给出的数值为n日高点和低点。
其次,K值为RSV的M日移动平均线,D值为K值的N日移动平均线,J值为3K-2D。
KDJ目标的规矩如下:
1. 当K值大于D值时,行情有利多方;
2. 当K值小于D值时,行情有利空方;
3. 当K值从上向下穿过D值时,向下跌破,为卖出信号,反之为买入信号;
4. K值大于80时为超买区,K值小于20时为超卖区。
2. KDJ的作用
KDJ目标是衡量股票价格动摇强度的一种技能剖析东西。KDJ是经过当时股价与最近n天的最高价和最低价比较得出的随机目标。首要用于研究商场超买和超卖情况、剖析股价走势的强弱和买卖信号。
3. KDJ的优缺点
在使用KDJ目标时,需要留意以下几点:
1. KDJ目标关于短期趋势的剖析较为灵敏,但关于长期趋势的剖析能力较弱;
2. 股市处于震动状况时,KDJ动摇会较大,难以精确判别买卖点;
3. 在前期下跌趋势中,KDJ目标会一直处在超卖区,难以判别止损点。
4. KDJ的使用
KDJ目标能够使用于股票、期货等商场中,评价商场情况,辅助决策。在实际操作过程中,能够配合其他技能目标和相关信息归纳剖析,进步精确性。
相关文章:

途乐证券-KDJ分别代表什么?
KDJ是一种技能剖析东西,常见于股票、期货等商场中,它的全称是随机目标(KDJ)。KDJ目标包括三条线,分别为K线、D线和J线。那么,KDJ分别代表什么呢?本文将从多个视点进行剖析。 1. KDJ的简单介绍 …...

用C语言重写的原始Matlab OpenShoe算法:深入理解和实现步态分析的关键技术
一、引言 在许多领域,如医疗健康、体育科学、虚拟现实和机器人技术中,步态分析都是一个重要的研究领域。步态分析可以帮助我们理解人体运动的机制,评估疾病的影响,优化运动员的表现,甚至设计更自然的机器人运动。Open…...

什么开放式耳机音质好?值得推荐的开放式耳机分享
与封闭式耳机相比,开放式耳机具有更为自然、真实的音质,能够更好地还原音乐现场的声音环境。以下是几款值得推荐的开放式耳机,都来看看有哪些吧。 推荐一:NANK南卡00压开放式耳机 点评:体验最好的开放式耳机没有之一…...

mac harbor的安装
harbor的安装 为什么要整这个呢,因为我在学习k8s,但是需要一个自己的镜像仓库。于是,最开始想到的就是在本地直接部署一个,还比较安全、快速。 直接下载了官方的项目,运行脚本发现出了异常,这种异常我已经…...

SetActive和Enable有什么不同?
介绍 在Unity中,SetActive和Enable都是常用的方法,用于在运行时控制对象的可见性和功能开启状态。尽管它们的目的相似,但在使用时有一些区别。 SetActive SetActive是GameObject类的方法,用于启用或禁用游戏对象及其所有子对象…...
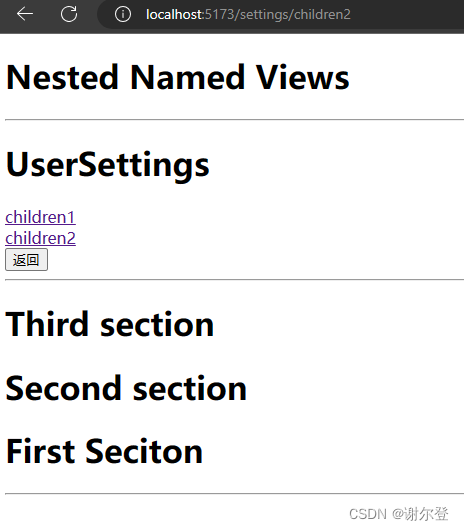
【Vue-Router】重定向
First.vue <template><h1>First Seciton</h1> </template>Second.vue,Third.vue代码同理 UserSettings.vue <template><h1>UserSettings</h1><router-link to"/settings/children1">children1</ro…...

vulnhub靶场之ADROIT: 1.0.1
准备: 攻击机:虚拟机kali、本机win10。 靶机:Adroit: 1.0.1,下载地址:https://download.vulnhub.com/adroit/Adroit-v1.0.1.ova,下载后直接vbox打开即可。 知识点:shell反弹(jar&…...
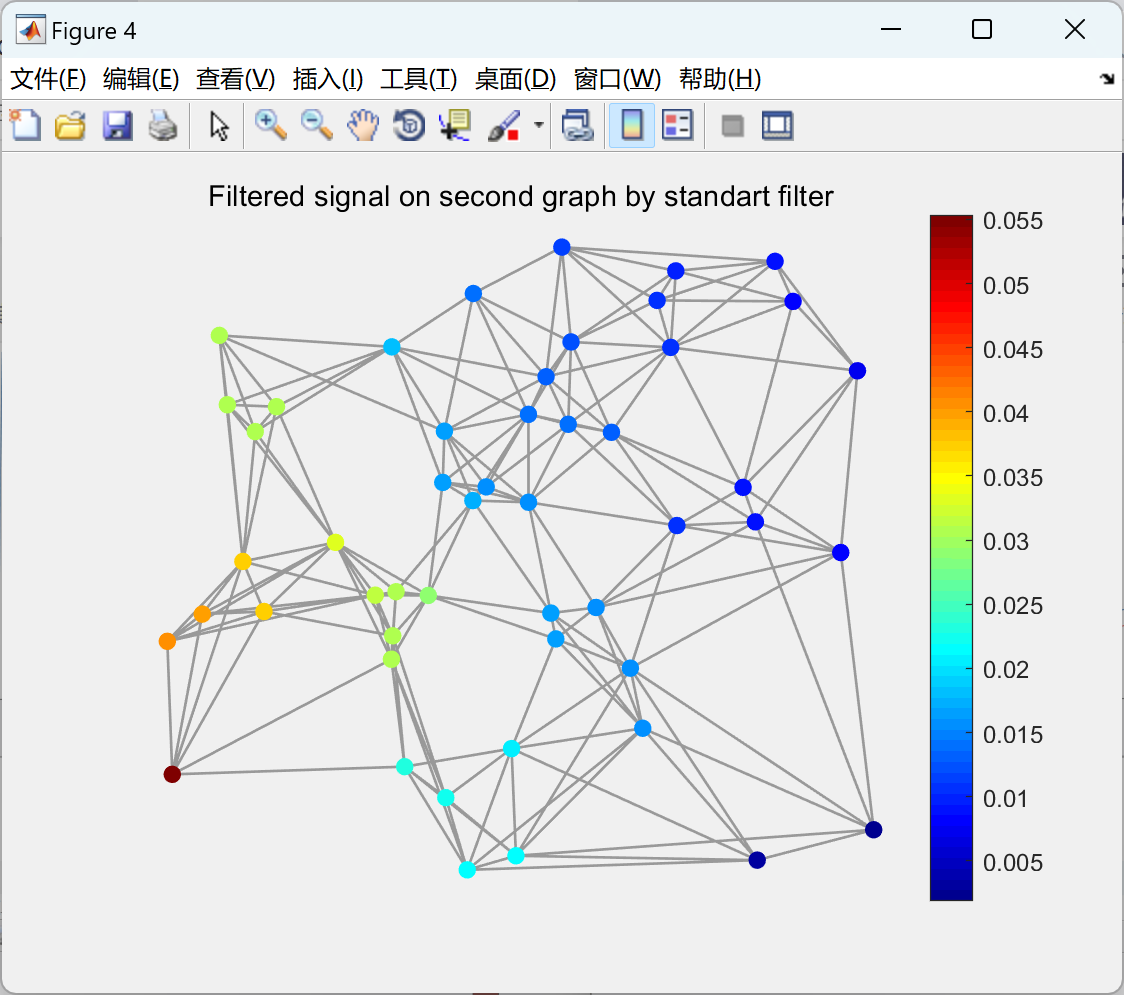
【非欧几里得域信号的信号处理】使用经典信号处理和图信号处理在一维和二维欧几里得域信号上应用低通滤波器研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
【深入理解ES6】字符串和正则表达式
概念 字符串(String)是JavaScript6大原始数据类型。其他几个分别是Boolean、Null、Undefined、Number、Symbol(es6新增)。 更好的Unicode支持 1. UTF-16码位 字符串里的字符有两种: 前 个码位均以16位的编码单元…...

易服客工作室:Pixwell主题 – 现代杂志/WordPress新闻主题
PixWell主题概述 Pixwell主题是一个强大、多用途和现代的WordPress杂志主题,具有像素完美的设计、出色的功能、完全响应和移动友好。它非常灵活,非常适合食谱、时尚、旅行、技术、个人或任何其他很棒的杂志和博客网站。 该主题与 Elementor、Cooked&am…...
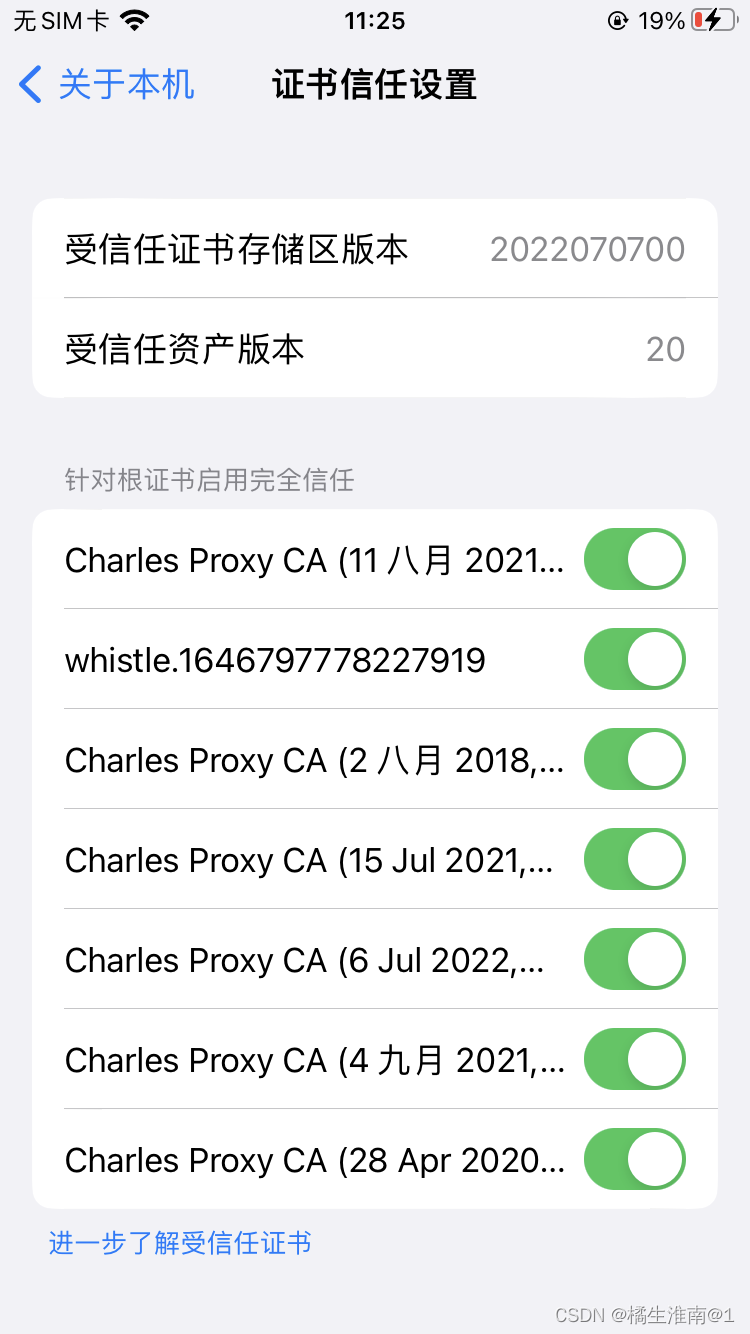
iOS手机无法安装Charles 的ssl证书
问题描述 iOS客户端安装证书时一直卡在下载这一步,无法抓包 1、打开Charles,选择help→SSL Proxying→Install Charles Root Certificate on a Mobile Device or Remote Browser 2、按照步骤1中的提示进行操作,手机连接电脑代理,…...

Promise处理异步操作
Promise是一种在JavaScript中处理异步操作的技术。Promise对象表示一个尚未完成的异步操作,它可以在将来的某个时候产生结果。Promise对象的状态可以是未完成、已完成或已拒绝。当Promise对象处于未完成状态时,我们可以附加一个或多个处理程序࿰…...
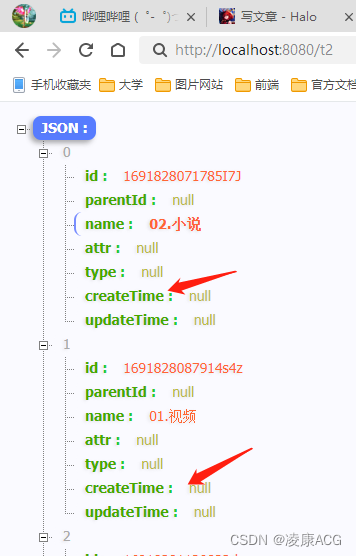
jpa查询返回自定义对象、返回指定VO、POJO
jpa查询返回自定义对象、返回指定VO、POJO jpa查询返回自定义对象、返回指定VO、POJO,JPA查询前会做大量处理,还有线程通知的操作。若并发大,处理性能直线下降。但是jpa就因为做了大量处理,对多数据库兼容极好,操作方…...
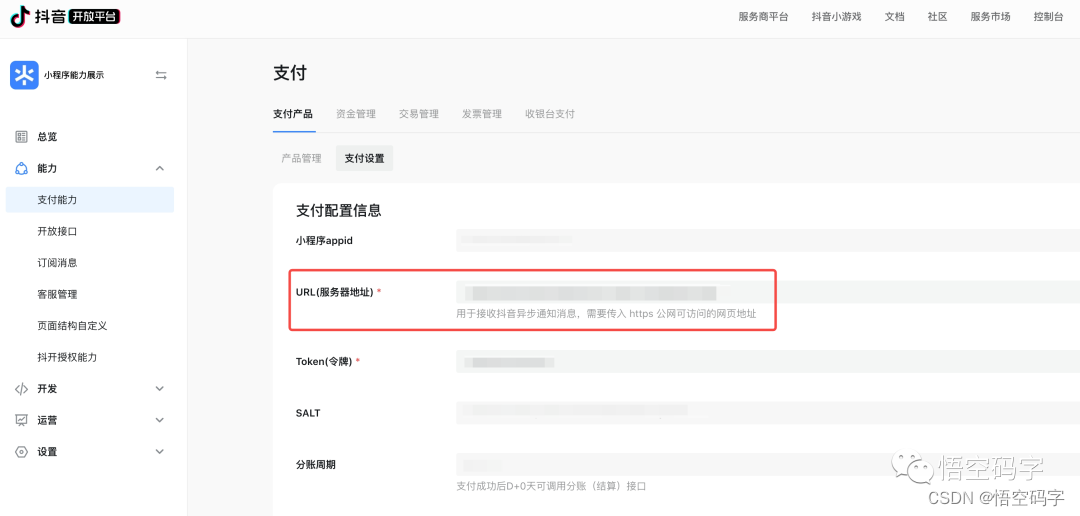
抖音小程序开发,收银台支付回调通知
大家好,我是小悟 关于抖音小程序收银台支付,可阅读【抖音小程序开发,唤起收银台,包括抖音支付、支付宝支付、微信支付】。 做支付功能最重要的一步就是异步回调通知,所谓回调通知就是唤起收银台支付,支付…...

selenium 爬虫
selenium 可以动态爬取网页数据,就像真实用户操作浏览器一样,从终端用户的角度测试应用程序,WebDriver通过原生浏览器支持或者浏览器扩展直接控制浏览器 webdriver下载 因为selenuim对浏览器的版本存在兼容问题,顾需要针对指定浏…...

亚商投资顾问 早餐FM/0815生成式人工智能服务管理
01/亚商投资顾问 早间导读 商务部等9部门:促进农村大宗商品消费更新换代中央财办等九部门印发指导意见推动农村流通高质量发展《生成式人工智能服务管理暂行办法》今起施行 02/亚商投资顾问 新闻早餐 // 热点聚焦 // 商务部等9部门印发《县域商业三年行动计划&…...

C语言题目的多种解法分享 2之字符串左旋和补充题
前言 有的时候,这个系列专栏中的解法之间并无优劣,只是给大家提供不同的解题思路 我决定将代码实现的过程写成注释,方便大家直接找到对应的函数,只有需要补充说明的知识才会单拿出来强调 这个系列的文章会更的比较慢࿰…...

科技云报道:算力之战,英伟达再度释放AI“炸弹”
科技云报道原创。 近日,在计算机图形学顶会SIGGRAPH 2023现场,英伟达再度释放深夜“炸弹”,大模型专用芯片迎来升级版本。 英伟达在会上发布了新一代GH200 Grace Hopper平台,该平台依托于搭载全球首款搭载HBM3e处理器的新型Grac…...

油电同价、标配8155,奇瑞猛攻10-15万中型SUV市场
8月8日,奇瑞瑞虎8冠军家族在北京国家奥林匹克体育中心正式上市,推出了瑞虎8 PRO冠军版、瑞虎8新能源冠军版两款新车,燃油混动双线同步发力。 其中,瑞虎8 PRO冠军版共推7款车型,官方指导价12.69万元-16.39万元…...
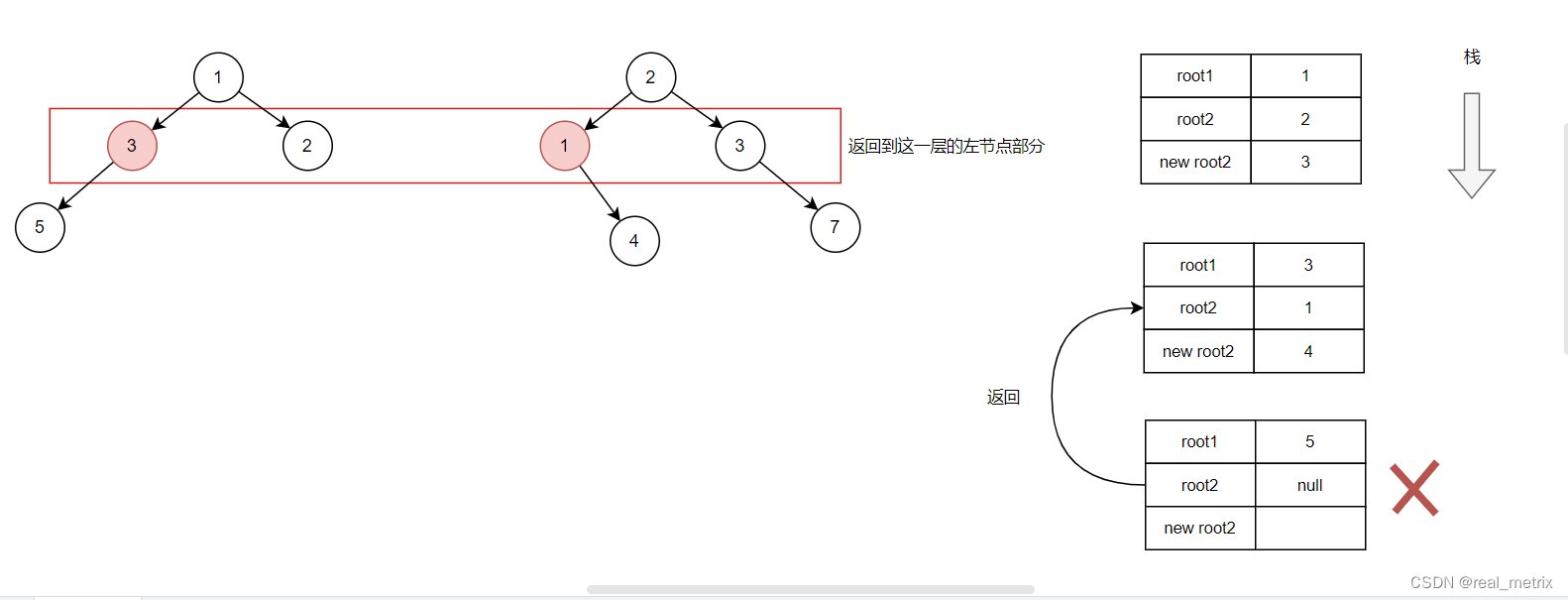
【leetcode】【图解】617. 合并二叉树
题目 难度:简单 给你两棵二叉树: root1 和 root2 。 想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
