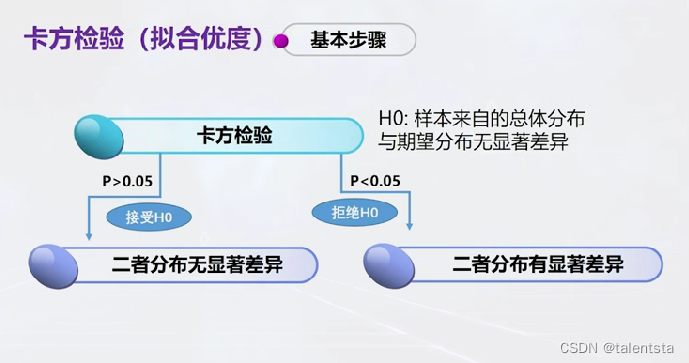
推断统计中非参数检验之卡方检验、列联表分析和游程检验
一、(卡方检验):赛马比赛的赛道会影响成绩吗
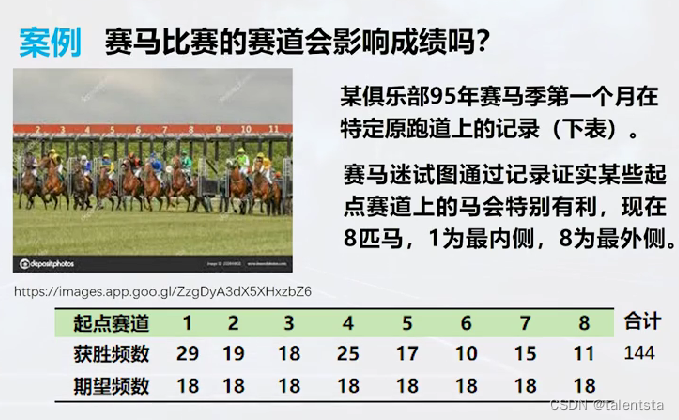
这里以一个实例赛马比赛的赛道是否会影响成绩为例,实际就是检验获胜频数与期望频数之间有无显著性差异。


import pandas as pd'''step1 调用包'''
from scipy.stats import chisquare
import numpy as np'''step2 读(导)入数据'''
# f_obs = np.array([29,19,18,25,17,10,15,11])
# f_exp = np.array([18,18,18,18,18,18,18,18])
data = pd.read_excel('data_chi2.xlsx')
f_obs=data.qi
f_exp=data.ping
'''Step3 卡方检验'''
chi = chisquare(f_obs,f_exp)
print('卡方统计量值为:',np.round(chi[0],3))
print('\n P值为:',np.round(chi[1],3))
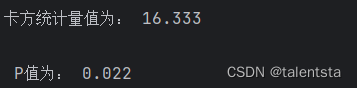
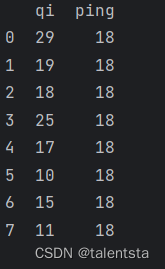
这里我们进行卡方分析的导入的包是从 scipy 中导入 chisquare进行分析,同时这里我们读取或者直接导入数据都是可以的,都可以经过分析产生一样的结果。经过分析我们这里求出的p值为0.022,是小于0.05的,此时我们应该拒绝原假设,认为二者分布有显著性差异,即赛马比赛的赛道会影响成绩。
二、(列联表分析):感冒与是否喝牛奶有关吗?

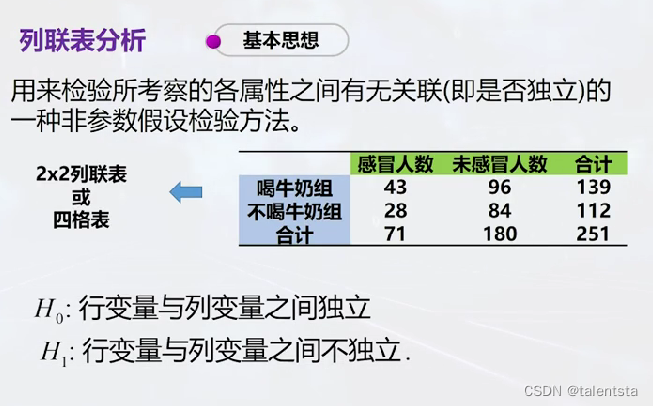

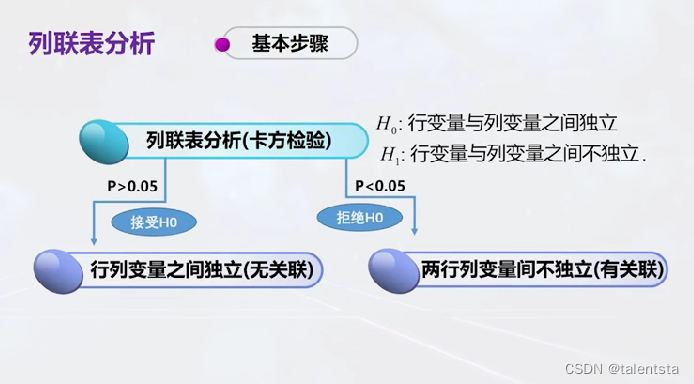
原假设是行变量与列变量之间是相互独立的,也就是是否感冒与是否喝牛奶之间没有关系,同时此时的检验统计量选择的卡方检验,决策方法依然是采用p值进行决策。

'''step1 调用包'''
from scipy.stats import chi2_contingency
import numpy as np'''step2 读(导)入数据'''
data = np.array([[43,96], [28,84]])'''Step3 列联表分析(卡方检验)'''
chi = chi2_contingency(data)
print('卡方统计量值为:',np.round(chi[0],3))
print('\n P值为:',np.round(chi[1],3))
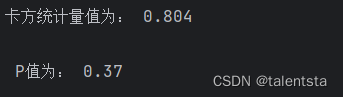

从这里我们可以看出此时的p值为0.37,此时不能拒绝原假设,认为感冒与喝牛奶之间相互独立,感冒与否与是否喝牛奶之间没有关联。
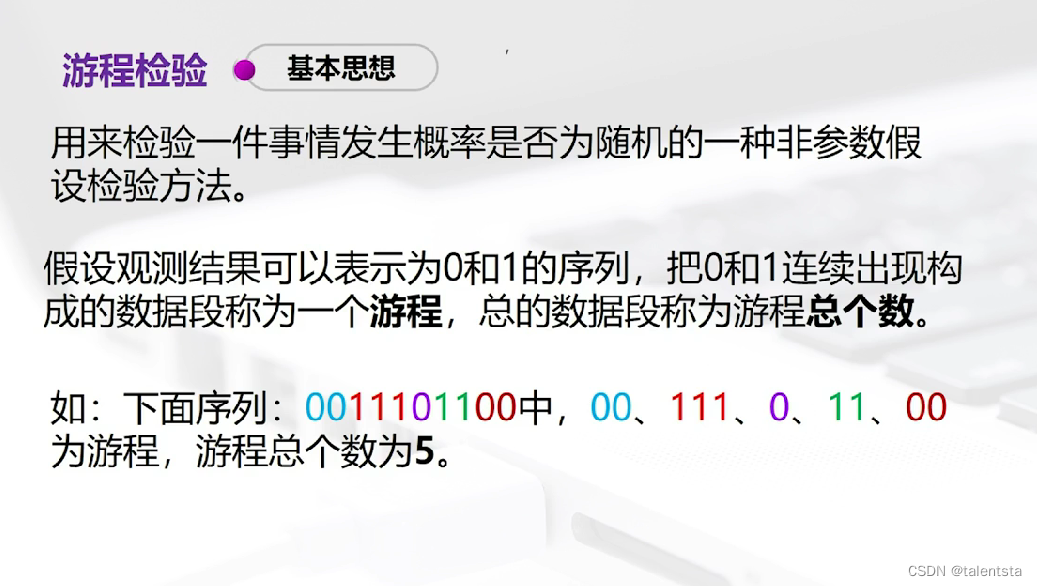
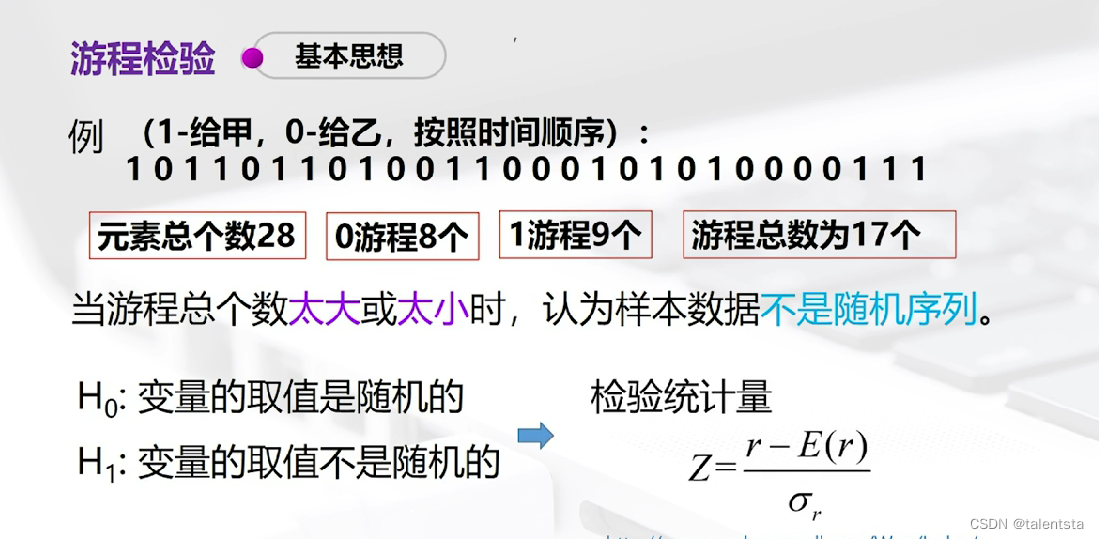
三、(游程检验):足球裁判执法公平吗?


'''step1 调用包'''
from statsmodels.sandbox.stats.runs import runstest_1samp
import numpy as np'''step2 读(导)入数据'''
seq =np.array([1,0,1,1,0,1,1,0,1,0,0,1,1,0,0,0,1,0,1,0,1,0,0,0,0,1,1,1])'''Step3 游程检验'''
res = runstest_1samp(seq)
print('Z统计量值为:',np.round(res[0],3))
print('\n P值为:',np.round(res[1],3))
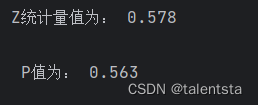
从这里我们可以看到此时的p值为0.563,我们不能拒绝原假设,认为此时的变量取值是随机的,也就是足球裁判执法是公平的。
从这我们也可以归纳出假设检验的基本步骤就是读入数据之后选择合适的数据输入形式,此时根据不同的检验统计量,不一样的检验方法的检验统计量也不同。
相关文章:

推断统计中非参数检验之卡方检验、列联表分析和游程检验
一、(卡方检验):赛马比赛的赛道会影响成绩吗 这里以一个实例赛马比赛的赛道是否会影响成绩为例,实际就是检验获胜频数与期望频数之间有无显著性差异。 import pandas as pdstep1 调用包 from scipy.stats import chisquare impor…...

AI社交来了,百度、Soul“双向奔赴”
随着科技的飞速进步和迅猛发展,AI技术已经开始渗透到教育、工作、社交、娱乐和健康多个领域,并为人们生活中的多个场景带来了诸多的创新和可能性。甚至可以说,AI技术已经深刻地介入到了我们日常生活的方方面面,让我们的生活方式发…...
【【verilog 典型电路设计之加法器树乘法器】】
verilog 典型电路设计之加法器树乘法器 加法器树乘法器 加法器树乘法器的设计思想是“移位后加”,并且加法运算采用加法器树的形式。乘法运算的过程是,被乘数与乘数的每一位相乘并且乘以相应的权值,最后将所得的结果相加,便得到了…...

选择最适合自己的NIO, 一探流技术
目录 一、Channel1、FileChannel代码示例2、DatagramChannel代码示例3、SocketChannel 和 ServerSocketChannel代码示例 二、Buffer1、ByteBuffer示例代码2、CharBuffer示例代码3、ShortBuffer、IntBuffer、LongBuffer、FloatBuffer、DoubleBuffer 等示例代码 三、Selector1、S…...
---socket网络控制线程封装)
智能家居(3)---socket网络控制线程封装
封装socket网络线程实现对智能家居中各种灯光的控制 main.Pro(主函数) #include <stdio.h> #include "controlDevice.h" #include "inputCommand.h" #include <pthread.h>struct Devices *pdeviceHead NULL; //设备工厂链表…...

ubuntu 安装 emscripten 时 install latest 安装报错问题
学习官网参考:Compiling a New C/C Module to WebAssembly - WebAssembly | MDN (mozilla.org) 报错信息 形如: Error: Downloading URL https://storage.googleapis.com/webassembly/emscripten-releases-builds/linux/b90507fcf011da61bacfca613569…...
concrt140.dll丢失怎么恢复?教你5种修复方法
首先介绍一下concrt140.dll是什么 concrt140.dll是Microsoft Visual C Redistributable for Visual Studio 2015所需的一个动态链接库文件。它是用于支持C程序运行的重要组件之一。当系统中缺少或丢失concrt140.dll文件时,可能会导致一些程序无法正常运行。 首先&a…...

【Vue-Router】路由入门
路由(Routing)是指确定网站或应用程序中特定页面的方式。在Web开发中,路由用于根据URL的不同部分来确定应用程序中应该显示哪个内容。 构建前端项目 npm init vuelatest //或者 npm init vitelatest安装依赖和路由 npm install npm instal…...

蓝牙耳机运动耳机哪个好、好用的运动蓝牙耳机推荐
如今的蓝牙耳机已经成为手机的最佳伴侣,也是运动爱好者的必备装备。然而,在众多蓝牙耳机中做出选择可能会让人感到困惑。其实,在选购运动蓝牙耳机时需要注意的事项还挺多的,比如舒适度、稳定性和音质等多个方面,逐一对照这些要点来…...

大数据面试题:Kafka的ISR机制
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:1)从ISR踢出去之后呢;2)一般Leader怎么判断Follower挂掉? 参考答案: …...

Windows:解决MySQL登录ERROR 1045 (28000): Access denied for user ‘root‘@‘localhost‘ (using passwor=YES)问题
我在下载的MySQL是8.0.32版本,刚下的时候没什么问题第二天启动MySQL服务就出现了 ERROR 1045 (28000): Access denied for user rootlocalhost (using password: YES) 或 ERROR 1045 (28000): Access denied for user rootlocalhost (using password: NO) 这样的问题…...
springboot整合kafka多数据源
整合kafka多数据源 项目背景依赖配置生产者消费者消息体 项目背景 在很多与第三方公司对接的时候,或者处在不同的网络环境下,比如在互联网和政务外网的分布部署服务的时候,我们需要对接多台kafka来达到我们的业务需求,那么当kafk…...
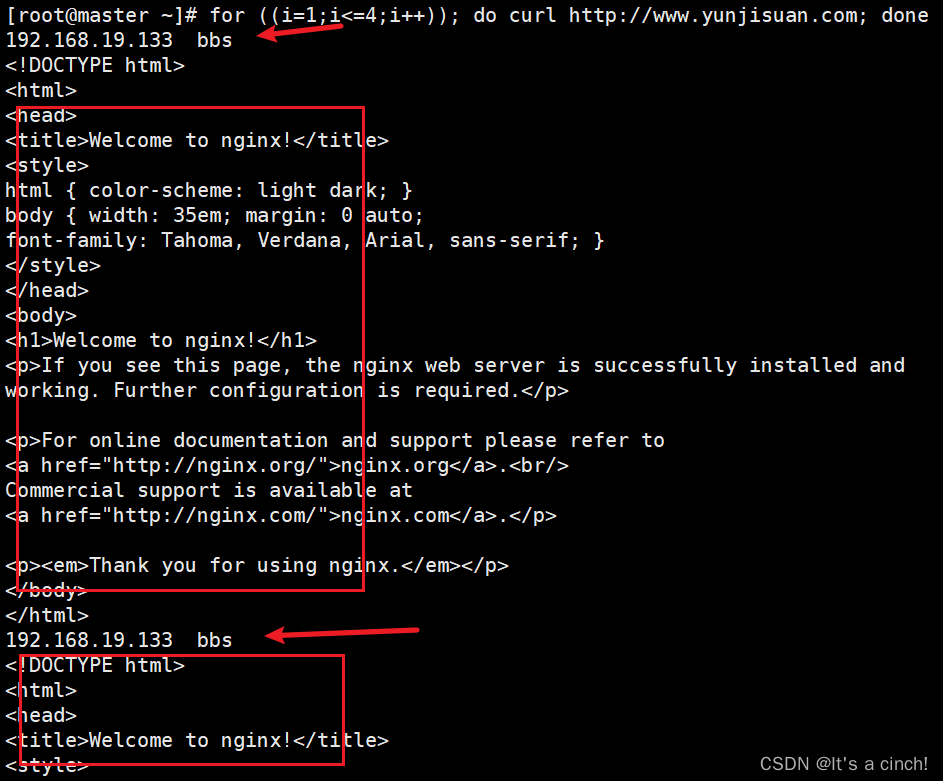
基于CentOS 7 配置nginx负载均衡
搭建负载均衡服务的需求如下: 1 ) 把单台计算机无法承受的大规模并发访问或数据流量分担到多台节点设备上,分别进行处理, 减少用户等待响应的时间, 提升用户体验。 2 ) 单个重负载的运算分担到多台节点设备上做并行处理ÿ…...

WordToPDF2.java
用Java将Word转PDF 本例子测试了spire.doc.free-3.9.0.jar的包 <dependency><groupId> e-iceblue </groupId><artifactId>spire.doc.free</artifactId><version>3.9.0</version></dependency> package word;import com.spire.…...

k8s服务注册发现
Service 是 将运行在一个或一组pod上的网络应用程序公开为网络服务的方法。 定义service前端为service名称、ip、端口等不变的部分,后端为符合标签选择的pod集合 注册 通过api server提交注册service请求到DNSservice随后得到clusterIP(虚拟ip地址&am…...
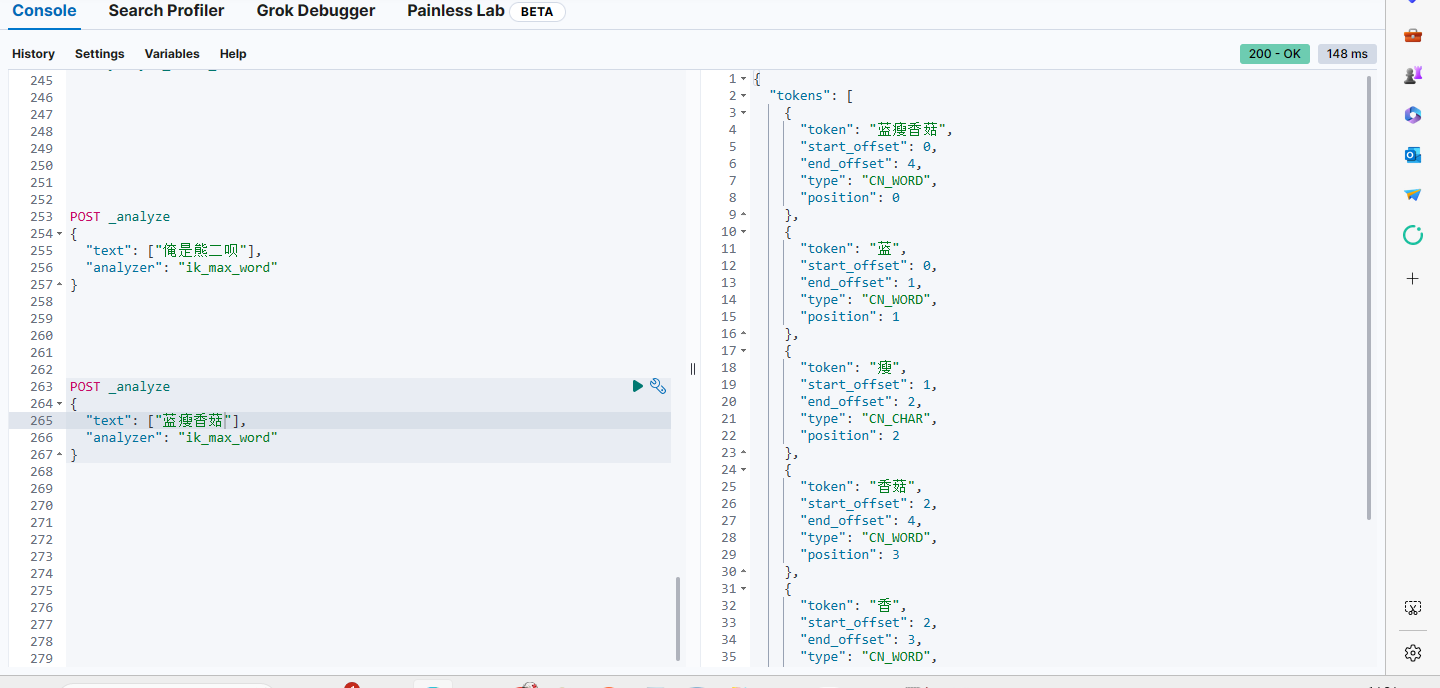
IK分词器升级,MySQL热更新助一臂之力
ik分词器采用MySQL热更新 官方所给的IK分词器只支持远程文本文件热更新,不支持采用MySQL热更新,没关系,这难不倒伟大的博主,给哈哈哈。今天就来和大家讲一下如何采用MySQL做热更新IK分词器的词库。 一、建立数据库表 CREATE…...
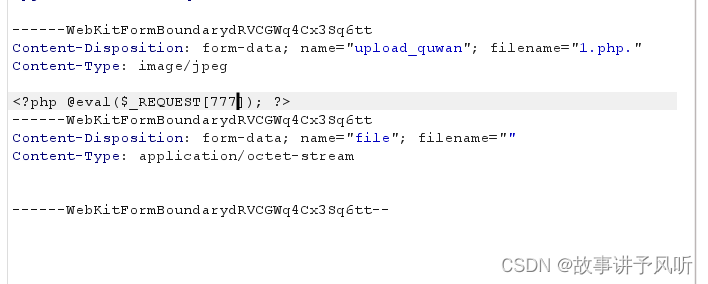
泛微 E-Office文件上传漏洞复现
声明 本文仅用于技术交流,请勿用于非法用途 由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,文章作者不为此承担任何责任。 文章作者拥有对此文章的修改和解释权。如欲转载或传播此文章,…...

bug的生命周期
bug的生命周期 bugbug的生命周期bug等级 bug 当且仅当规格说明书是存在的并且正确的,程序和规格说明书之间的不匹配才是错误当产品规格说明书没有提到时,以用户需求为准,当程序最终没有实现用户的合理预期的功能要求时,就是软件错…...

mysql分库分表相关
3小时快速上手sharding-jdbc 百亿级数据 分库分表 后面怎么分页查询? Java实战:教你如何进行数据库分库分表...

云原生k8s---资源限制、探针
目录 一:资源限制 1、资源限制原因 2、Pod 和 容器 的资源请求和限制 3、CPU 资源单位 4、内存 资源单位 5、事例 (1)事例一 (2)事例二 二:重启策略 1、重启策略模式 2、事例 三:探针…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...

Vuex:Vue.js 应用程序的状态管理模式
什么是Vuex? Vuex 是专门为 Vue.js 应用程序开发的状态管理模式 库。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。 在大型单页应用中,当多个组件共享状态时,简单的单向数据流…...
