LeetCode 1572. 矩阵对角线元素的和
【LetMeFly】1572.矩阵对角线元素的和
力扣题目链接:https://leetcode.cn/problems/matrix-diagonal-sum/
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
示例 1:
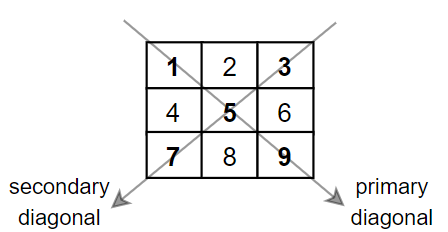
输入:mat = [[1,2,3],[4,5,6],[7,8,9]] 输出:25 解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25 请注意,元素 mat[1][1] = 5 只会被计算一次。
示例 2:
输入:mat = [[1,1,1,1],[1,1,1,1],[1,1,1,1],[1,1,1,1]] 输出:8
示例 3:
输入:mat = [[5]] 输出:5
提示:
n == mat.length == mat[i].length1 <= n <= 1001 <= mat[i][j] <= 100
方法一:模拟
假设 m a t mat mat的大小是 n × n n\times n n×n,则可以:
用 i i i从 0 0 0到 n − 1 n - 1 n−1遍历 m a t mat mat的每一行, a n s ans ans加上这一行的 i i i和 n − i − 1 n - i - 1 n−i−1。
最后,如果 n n n是奇数,则还需要减去对主副对角线重叠的元素 m a t [ ⌊ n 2 ⌋ ] [ ⌊ n 2 ⌋ ] mat[\lfloor\frac{n}{2}\rfloor][\lfloor\frac{n}{2}\rfloor] mat[⌊2n⌋][⌊2n⌋]
- 时间复杂度 O ( n ) O(n) O(n),其中 s i z e ( m a t ) = n × n size(mat) = n\times n size(mat)=n×n
- 空间复杂度 O ( 1 ) O(1) O(1)
AC代码
C++
class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size();int ans = 0;for (int i = 0; i < n; i++) {ans += mat[i][i] + mat[i][n - i - 1];}if (n % 2) {ans -= mat[n / 2][n / 2];}return ans;}
};
Python
# from typing import Listclass Solution:def diagonalSum(self, mat: List[List[int]]) -> int:n = len(mat)ans = 0for i in range(n):ans += mat[i][i] + mat[i][n - i - 1]if n % 2:ans -= mat[n // 2][n // 2]return ans
同步发文于CSDN,原创不易,转载请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/132223172
相关文章:

LeetCode 1572. 矩阵对角线元素的和
【LetMeFly】1572.矩阵对角线元素的和 力扣题目链接:https://leetcode.cn/problems/matrix-diagonal-sum/ 给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 示例 1&…...

SQLSERVER 查询语句加with (NOLOCK) 报ORDER BY 报错 除非另外还指定了 TOP、OFFSET 或 FOR XML
最近有一个项目在客户使用时发现死锁问题,用的数据库是SQLSERVER ,死锁的原因是有的客户经常去点报表,报表查询时间又慢,然后又有人在做单导致了死锁,然后主管要我们用SQLSERVER查询时要加with (NOLOCK),但是我在加完 …...

创建react native项目的笔记
创建react native项目的笔记 重新下载 ruby安装 watchman安装 cocoapods安装 react native 项目创建好项目后安装 ios 依赖清除设备缓存安装 android 依赖链接 网易 mumu 模拟器安装路由 Navigation页面之间的跳转逻辑自定义头部样式判断不同设备平台代码示例安装 Axios安装本地…...

Java自动化测试之Chrome网页爬取
记录一个好玩的小插件,可以通过它获取网页上的某个元素,然后得到他的值,不过需要懂前端技术,同时还需要一个chrome的小工具,工具放在我的共享文件里了,叫 chromedriver插件 pom 依赖 <dependency>&…...

boost下的asio异步高并发tcp服务器搭建
C 网络编程 asio 使用总结 - 知乎 (zhihu.com) 基于Boost::asio的多线程异步TCP服务器,实现了io_service线程池,测试了1万左右的并发访问,读写无压力_boost asio支持最大并发_E404的博客-CSDN博客 单线程 server.cpp #include <cstdlib&g…...
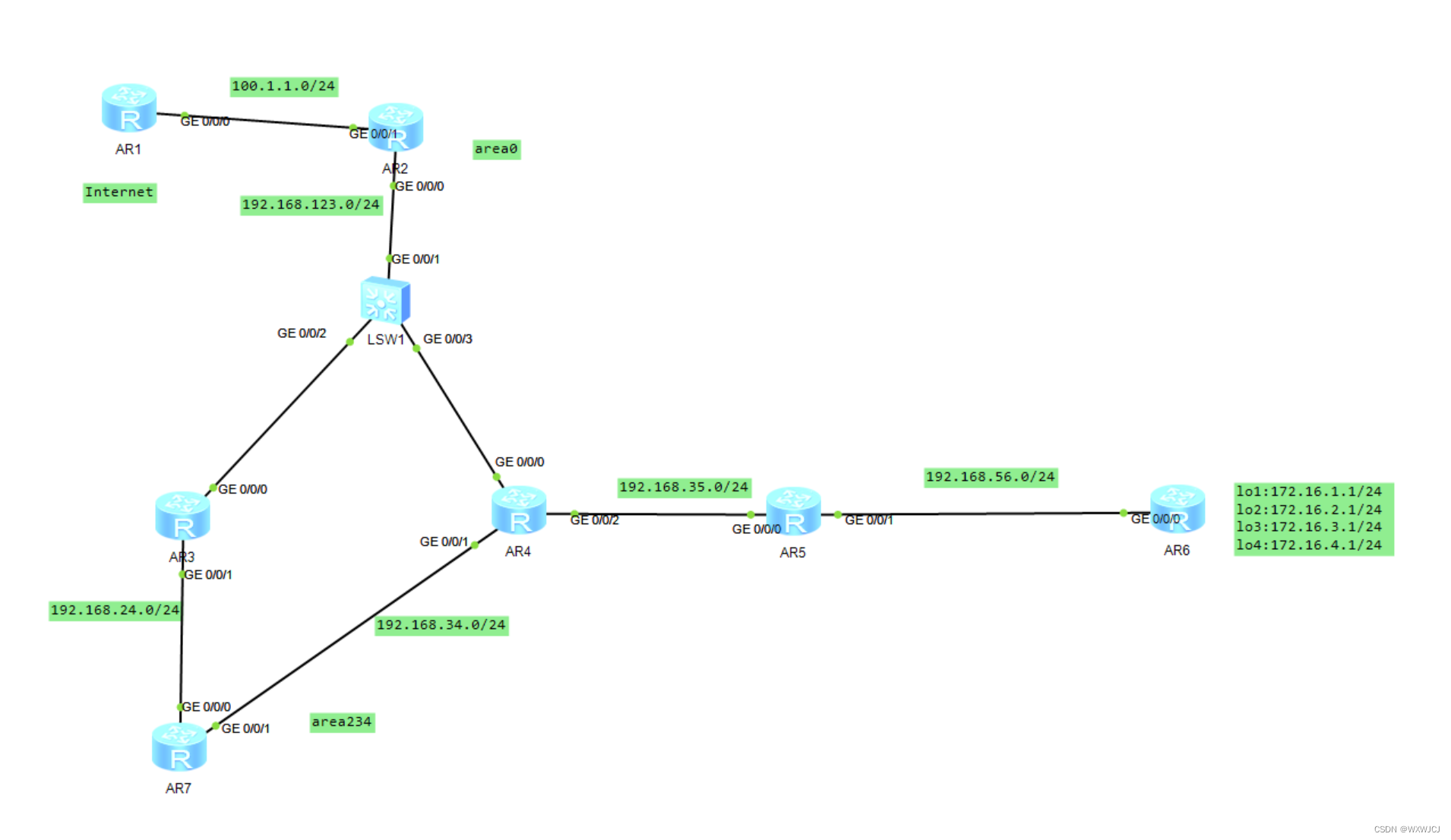
HCIP第五节------------------------------------------ospf
一、OSPF基础 1、动态路由分类 2、距离矢量协议 运行距离矢量路由协议的路由器周期性地泛洪自己的路由表。通过路由的交互,每台路由器都从相邻的路由器学习到路由,并且加载进自己的路由表中,然后再通告给其他相邻路由器。 对于网络中的所有…...

Golang下载安装
目录 1. 下载压缩包 2. 解压 3. 查看SDK是否安装成功 4. 配置环境变量 5. 查看环境变量是否配置成功 1. 下载压缩包 官网下载地址: All releases - The Go Programming Language Windows64位选择如下下载: 2. 解压 解压后内容如下: …...

工作时使用redis,kafka查阅的资料链接
不分先后 一 、redis查阅地址 一篇文章讲清楚RedisRedis原理介绍一篇详文带你入门 Redis内存耗尽后Redis会发生什么Redis 深入了解键的过期时间redis持久化机制Redis延迟问题全面排障指南一文搞定Redis高级特性与性能调优Redis 在 Linux 系统的配置优化Redis 的延迟问题&…...
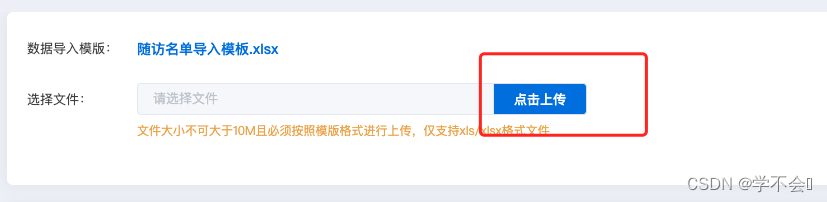
上传excel文件
文件上传,其实就是用el-upload组件来实现上传,只是换了样式,和图片上传一样 <el-form-item label"选择文件"><el-input placeholder"请选择文件" v-model"form.file" disabled style"width: 45…...

leetcode 力扣刷题哈希表初尝试
哈希表 刷题初尝试 哈希表基础知识242. 有效的字母异位词383. 赎金信49. 字母异位词分组438. 找到字符串中所有字母异位词 哈希表基础知识 哈希表是一种数据结构,也叫散列表。哈希表中存储的是键值对,即(key,value),根据key直接查…...
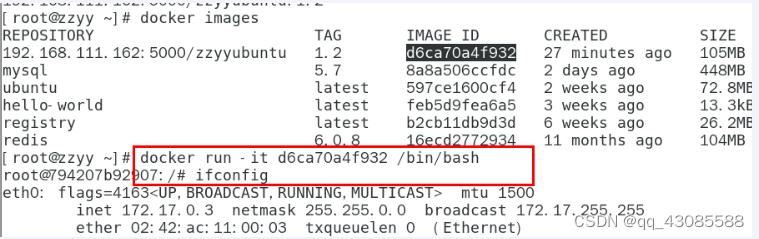
Docker 本地镜像发布到私有仓库
1. 本地镜像发布到私有库流程 2. 是什么 1 官方Docker Hub地址:https://hub.docker.com/,中国大陆访问太慢了且准备被阿里云取代的趋势,不太主流。 2 Dockerhub、阿里云这样的公共镜像仓库可能不太方便,涉及机密的公司不可能提供镜…...

计算机网络和 Internet 的基本概念
计算机网络和互联网(Internet)是现代计算机科技中的重要概念。它们为计算机之间的通信和数据交换提供了基础架构。以下是它们的基本概念: **计算机网络:** 计算机网络是指将多台计算机连接在一起,以便它们可以共享资…...

高并发数据抓取实战:使用HTTP爬虫ip提升抓取速度
又到每天一期学习爬虫的时间了,作为一名专业的爬虫程序员,今天要跟你们分享一个超实用的技巧,就是利用HTTP爬虫ip来提升高并发数据抓取的速度。听起来有点高大上?别担心,我会用通俗易懂的话来和你们说,让你…...

CSS3 中新增了哪些常见的特性?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 圆角(Border Radius)⭐ 渐变(Gradients)⭐ 阴影(Box Shadow)⭐ 文本阴影(Text Shadow)⭐ 透明度(Opacity)⭐ 过渡&…...

简单认识excel篇章1
excel是Office办公软件中的组件之一,它专长于对表格中的数据进行计算和统计管理,通常用于财务或其他数据管理的表格制作,同时excel还有很好的可视化能力,可用于制作各种行业报告。 在Microsoft Excel中,excel文件的后缀…...

CentOS系统环境搭建(九)——centos系统下使用docker部署项目
centos系统环境搭建专栏🔗点击跳转 关于Docker-compose安装请看CentOS系统环境搭建(三)——Centos7安装Docker&Docker Compose,该文章同样收录于centos系统环境搭建专栏。 Centos7部署项目 采用前后端分离的形式部署。使用Do…...
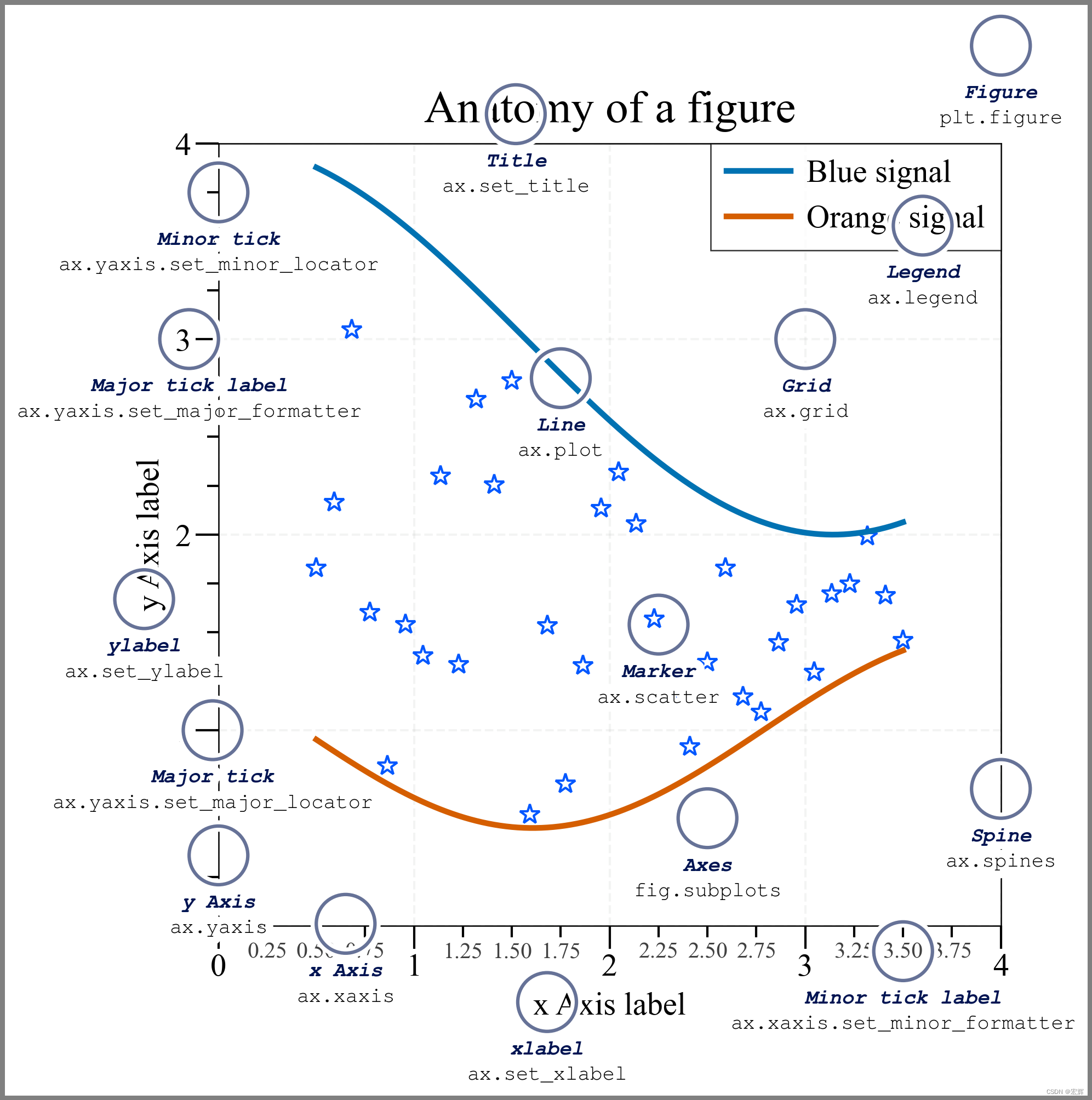
【科研论文配图绘制】task1 掌握科研绘图的基本知识
【科研论文配图绘制】task1 掌握科研绘图的基本知识 写在最前 8月份Datawhale组队学习,写下该博客记录学习内容 1.科研论文配图的分类与构成 2.科研论文配图的格式和尺寸 3.科研论文配图中的字体和字号设置 4.科研论文配图的版式设计、结构布局和颜色搭配 占个…...
YAML资源清单
目录 YAML资源清单 (一)YAML 语言 (1)基本语法 (2)支持的数据结构 (二)通过资源清单管理容器资源 YAML 语法格式: 创建Service资源清单 (三ÿ…...

数据分析两件套ClickHouse+Metabase(二)
Metabase篇 Metabase安装部署 任何问题请查看 -> 官方文档 jar包从GitHub下载 -> 地址 同样有个问题, 默认数据源里没有ClickHouse, 不过ClickHouse官方提供了插件包 -> 插件包 在安装metabase目录下新建一个plugins文件夹, 把下载的clickhouse.metabase-driver.ja…...

神经网络基础-神经网络补充概念-20-激活函数
概念 激活函数是神经网络中的一个重要组成部分,它引入了非线性性质,使得神经网络可以学习和表示更复杂的函数关系。激活函数对于将输入信号转换为输出信号起到了关键作用,它在神经元的计算过程中引入了非线性变换。 几种常见的激活函数及其…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
