day-18 代码随想录算法训练营(19)二叉树 part05
513.找树左下角的值
思路一:层序遍历,每一层判断是不是最后一层,是的话直接返回第一个;
如何判断是不是最后一层呢,首先队列头部,其次记录左右子节点都没有的节点数是不是等于que.size();或者直接判断队列是否为空。其实也不用判断,因为最后一次记录的队列头就是最左下角节点
class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*>que;que.push(root);int res=0;while(!que.empty()){int n=que.size();int mid=que.front()->val;for(int i=0;i<n;i++){TreeNode*node=que.front();que.pop();if(node->left)que.push(node->left);if(node->right)que.push(node->right);}if(que.empty())res=mid;}return res;}
};
思路二:递归,每次遍历到叶子节点时记录节点值和深度,使用数组,找到深度最深的第一个
class Solution {
public:vector<vector<int>> ans;void judge(TreeNode*root,int deepth){if(root==nullptr)return;if(root->left==nullptr && root->right==nullptr)ans.push_back({deepth,root->val});judge(root->left,deepth+1);judge(root->right,deepth+1);}int findBottomLeftValue(TreeNode* root) {judge(root,0);int mid=0,res=0;for(int i=0;i<ans.size();i++){if(ans[i][0]>mid){mid=ans[i][0];res=i;}}return ans[res][1];}
};思路三:递归,不使用额外空间,每次遍历到叶子节点是进行深度判断
class Solution {
public:int maxDeepth=-1;int res=0;void judge(TreeNode*root,int deepth){if(root==nullptr)return;if(root->left==nullptr && root->right==nullptr)//遍历到叶子节点时{if(deepth>maxDeepth){maxDeepth=deepth;res=root->val;}}judge(root->left,deepth+1);judge(root->right,deepth+1);}int findBottomLeftValue(TreeNode* root) {judge(root,0);return res;}
};注意:deepth是值传递,只有父节点的改变影响子节点的值;同为子节点是相互不影响的,所以相当于回溯了。
112.路径总和
思路:递归前序遍历二叉树,在叶子节点处进行判断
class Solution {
public:bool res=false;void judge(TreeNode*root,int targetSum,int sum){if(root==nullptr)return;if(root->left==nullptr && root->right==nullptr){if(sum+root->val==targetSum)res=true;//cout<<sum;}sum+=root->val;// if(sum>targetSum)// return;judge(root->left,targetSum,sum);judge(root->right,targetSum,sum);}bool hasPathSum(TreeNode* root, int targetSum) {judge(root,targetSum,0);return res;}
};113.路径总和||
思路一:还是直接递归,然后在叶子节点处判断
注意:每次当前节点判断完之后需要删除路径的最后一个节点,即回溯到另一个节点
class Solution {
public:vector<vector<int>>res;vector<int>mids;void judge(TreeNode*root,int targetSum,int sum){if(root==nullptr)return;if(root->left==nullptr && root->right==nullptr){if(sum+root->val==targetSum){mids.push_back(root->val);res.push_back(mids);mids.erase(mids.end()-1);return;}}sum+=root->val;mids.push_back(root->val);judge(root->left,targetSum,sum);judge(root->right,targetSum,sum);mids.erase(mids.end()-1);}vector<vector<int>> pathSum(TreeNode* root, int targetSum) {//思路一:直接递归,在叶子节点处判断if(root==nullptr)return vector<vector<int>>();judge(root,targetSum,0);return res;}
};106.从中序与后序遍历序列构造二叉树
分析:这个递归切割的想法很精妙
class Solution {
private:TreeNode*judge(vector<int>&inorder,vector<int>&postorder){if(postorder.size()==0) return NULL;//后续遍历数组最后一个元素,就是当前二叉树的中间节点int rootValue=postorder[postorder.size()-1];TreeNode*root=new TreeNode(rootValue);//叶子节点if(postorder.size()==1) return root;//找到中序遍历的切割点int midLastIndex;for(midLastIndex=0;midLastIndex<inorder.size();midLastIndex++){if(inorder[midLastIndex]==rootValue) break;}//切割中序数组//左闭右开区间[0,midLastIndex]vector<int> leftInorder(inorder.begin(),inorder.begin()+midLastIndex);vector<int> rightInorder(inorder.begin()+midLastIndex+1,inorder.end());//删除后序数组的末尾元素postorder.resize(postorder.size()-1);//切割后序数组//依然左闭右开,注意这里使用了左中序数组大小作为切割点vector<int> leftPostorder(postorder.begin(),postorder.begin()+leftInorder.size());vector<int> rightPostorder(postorder.begin()+leftInorder.size(),postorder.end());root->left=judge(leftInorder,leftPostorder);root->right=judge(rightInorder,rightPostorder);return root;}
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if(inorder.empty() || postorder.empty()) return nullptr;return judge(inorder,postorder);}
};105.从前序和中序遍历序列构造二叉树
分析:和中序和后序遍历序列构造二叉树几乎一摸一样
思路:每次构建中间节点,把前序和中序遍历序列进行分割,再递归到下一层,把分割后的序列传入下一层,最后依次把创建出来的中间节点返回给上一层连接(回溯)
class Solution {
public:TreeNode* judge(vector<int>&preorder,vector<int>&inorder){if(preorder.size()==0) return nullptr;int rootValue=preorder[0];TreeNode*root=new TreeNode(rootValue);if(preorder.size()==1) return root;//在中序序列中找到切割点int mid;for(mid=0;mid<inorder.size();mid++){if(inorder[mid]==rootValue) break;}//对中序遍历序列进行切割vector<int>leftInorder(inorder.begin(),inorder.begin()+mid);vector<int>rightInorder(inorder.begin()+mid+1,inorder.end());//删除中间节点preorder.erase(preorder.begin());//对前序遍历序列进行切割 注意,中间节点已经删除,所以第一个元素也为左边前序vector<int>leftPreorder(preorder.begin(),preorder.begin()+leftInorder.size());vector<int>rightPreorder(preorder.begin()+leftInorder.size(),preorder.end());//把切割后的序列传入下一层root->left=judge(leftPreorder,leftInorder);root->right=judge(rightPreorder,rightInorder);//把创建出来的中间节点传入上一层return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.empty() || inorder.empty()) return nullptr;return judge(preorder,inorder);}
};107.二叉树的层序遍历II
思路:简单的层序遍历,加入栈然后取出
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {//思路:层序遍历,然后把每一层的数据加入栈中,最后再从栈中取出vector<vector<int>>res;if(root==nullptr) return res;queue<TreeNode*>que;stack<vector<int>>midSt;que.push(root);while(!que.empty()){int n=que.size();vector<int>mids;for(int i=0;i<n;i++){TreeNode*cur=que.front();mids.push_back(cur->val);que.pop();if(cur->left) que.push(cur->left);if(cur->right) que.push(cur->right);}midSt.push(mids);}cout<<midSt.size();int len=midSt.size();for(int i=0;i<len;i++){res.push_back(midSt.top());midSt.pop();}return res;}
};今日问题:43.字符串相乘
849. 到最近的人的最大距离
相关文章:
二叉树 part05)
day-18 代码随想录算法训练营(19)二叉树 part05
513.找树左下角的值 思路一:层序遍历,每一层判断是不是最后一层,是的话直接返回第一个; 如何判断是不是最后一层呢,首先队列头部,其次记录左右子节点都没有的节点数是不是等于que.size();或…...

【数据结构OJ题】移除链表元素
原题链接:https://leetcode.cn/problems/remove-linked-list-elements/description/ 1. 题目描述 2. 思路分析 我们可以定义一个结构体指针变量cur,让cur一开始指向头结点,同时定义一个结构体指针prev,令prev初始化为空指针NULL…...

centos 安装 virtualbox
参考 https://phoenixnap.com/kb/how-to-install-virtualbox-centos-7 遇到 Gpg Keys Failue 这样解决 将 rpm 包下载到本地 –disablerepovirtualbox sudo yum --disablerepovirtualbox localinstall VirtualBox-7.0-7.0.10_158379_el7-1.x86_64 failure: repodata/repomd…...

Java8之Optional类的基本使用
文章目录 一、简介二、常见的Optional用法:1、创建Optional对象:1.1 使用of()方法:1.2 使用ofNullable()方法:1.3 使用empty()方法: 2、判断Optional是否包含值:2.1 使用isPresent()方法: 3、获…...

LinuxPTP时间同步
参考文献: http://linuxptp.sourceforge.net/ 0、硬件支持 查看网卡是否支持软硬件时间戳: sudo ethtool -T eno1 Time stamping parameters for eno1: Time stamping parameters for eno1: Capabilities: hardware-transmit (SOF_TIMESTAMPIN…...
【Django】Task1安装python环境及运行项目
【Django】Task1安装python环境及运行项目 写在最前 8月份Datawhale组队学习,在这个群除我佬的时代,写一下blog记录学习过程。 参考资源: 学习项目github:https://github.com/Joe-2002/sweettalk-django4.2 队长博客:…...
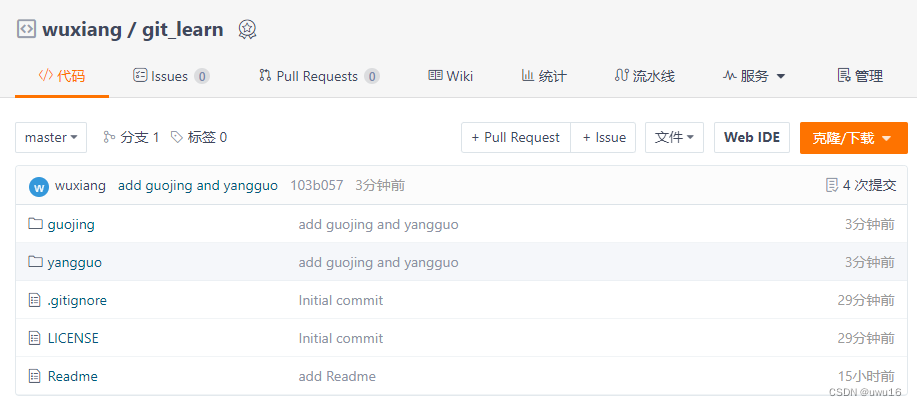
00 - 环境配置
查看所有文章链接:(更新中)GIT常用场景- 目录 文章目录 1. 环境说明2. 安装配置2.1 配置user信息2.2 config的三个作用域 3. 建git仓库3.1 把已有的项目代码纳入git管理3.2 新建的项目直接用git管理3.3 配置local的user和email3.4 优先级&…...
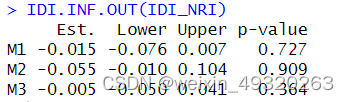
R语言实现计算净重新分类指数(NRI)和综合判别改善指数(IDI)
两个模型比较,与第一个模型相比,NRI(重新分对的 - 重新分错的)/总人数。IDI(新模型患者平均预测概率-旧模型患者平均预测概率)-(新模型非患者平均预测概率-旧模型非患者平均预测概率)…...

【面试总结】八股①
目录 数据库缓存穿透是什么常见的sql调优方法有哪些使用表的别名为什么能优化查询性能MySQL事务特性是哪些事务隔离级别有哪些 Java基础StringBuffer和StringBuilder的区别String直接引号新建和new String新建的区别Java中继承和实现的各种关系 消息队列Redis计算机常识缓冲击穿…...
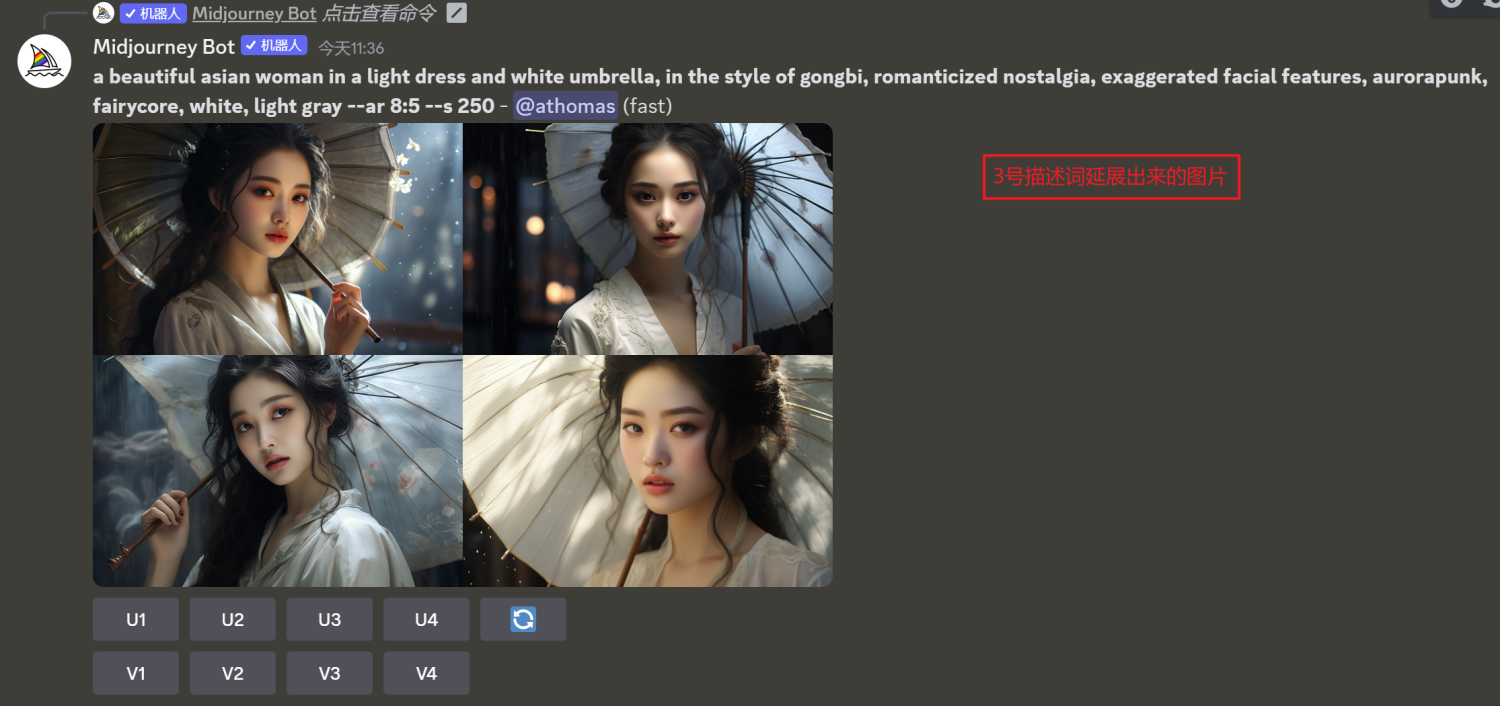
AI绘画 | 一文学会Midjourney绘画,创作自己的AI作品(快速入门+参数介绍)
一、生成第一个AI图片 首先,生成将中文描述词翻译成英文 然后在输入端输入:/imagine prompt:Bravely running boy in Q version, cute head portrait 最后,稍等一会即可输出效果 说明: 下面的U1、U2、U3、U4代表的第一张、第二张…...

MongoDB 数据库详细介绍
MongoDB 数据库详细介绍 MongoDB(来自“Humongous”,意为巨大的)是一个开源、高性能、无模式(NoSQL)、文档导向的分布式数据库。它以其灵活性、可扩展性和强大的查询功能而闻名于世。MongoDB 使用 JSON 格式的文档来存…...
Qt在mac安装
先在app store下载好Xcode 打开Xcode 随便建个文件给它取个名字找个地方放提醒没建立git link,不用理他打开终端, 输入/usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"...

STM32 F103C8T6学习笔记1:开发环境与原理图的熟悉
作为一名大学生,学习单片机有一段时间了,也接触过嵌入式ARM的开发,但从未使用以及接触过STM32C8T6大开发使用,于是从今日开始,将学习使用它~ 本文介绍STM32C8T6最小系统开发环境搭建注意问题,STM32C8T6单片…...

【Linux命令详解 | ps命令】 ps命令用于显示当前系统中运行的进程列表,帮助监控系统状态。
文章标题 简介一,参数列表二,使用介绍1. 基本用法2. 显示所有进程3. 显示进程详细信息4. 根据CPU使用率排序5. 查找特定进程6. 显示特定用户的进程7. 显示进程内存占用8. 查看进程树9. 实时监控进程10. 查看特定进程的详细信息11. 查看特定用户的进程统计…...

“超越传统的HTTP请求:深度解析Axios,打造前端开发的终极利器“
解锁前端开发的新境界 - 深入探索Axios,构建卓越的互联网应用 在当今数字化世界中,互联网应用的需求日益增长,而无论是大型企业还是初创公司,都需要一个强大而可靠的工具来处理与后端服务器之间的通信。这就是Axios的光辉时刻。作…...
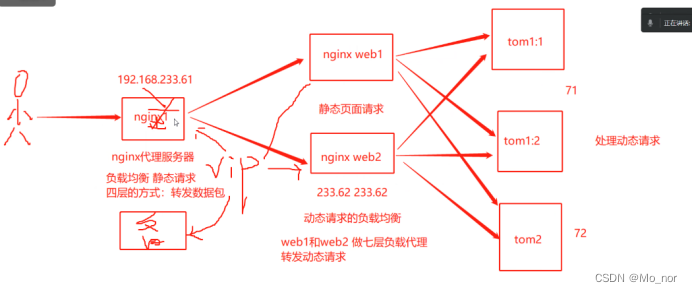
【Tomcat】tomcat的多实例和动静分离
多实例: 在一台服务器上有多台Tomcat;就算是多实例 安装telnet服务,可以用来测试端口通信是否正常 yum -y install telnettelnet 192.168.220.112 80 tomcat的日志文件 cd /usr/local/tomcat/logsvim catalina.out Tomcat多实例部署&…...

Python爬虫IP代理池的建立和使用
写在前面 建立Python爬虫IP代理池可以提高爬虫的稳定性和效率,可以有效避免IP被封锁或限制访问等问题。 下面是建立Python爬虫IP代理池的详细步骤和代码实现: 1. 获取代理IP 我们可以从一些代理IP网站上获取免费或付费的代理IP,或者自己租…...
)
Java面试题(dubbo)
目录 什么是dubbo?为什么要用? dubbo的使用场景和核心功能? dubbo核心组件 dubbo服务注册与发现的流程 dubbo与spring的关系 dubbo与springCloud的区别 dubbo有哪些注册中心? dubbo使用的什么通讯框架? dubbo…...

JVM源码剖析之Caused by: java.lang.OutOfMemoryError: GC overhead limit exceeded异常
写在前面: 版本信息: jdk版本:jdk8u40 垃圾回收器:ParallelScavenge new/old最近在群里看到有一位老哥拿着异常信息到处问,而发生的就是java.lang.OutOfMemoryError: GC overhead limit exceeded异常,恰好…...
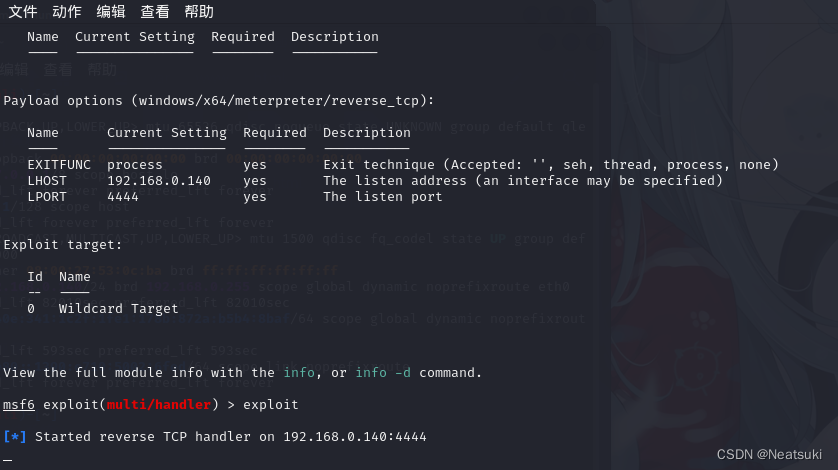
使用PDF文件入侵任何操作系统
提示:我们8月28号开学,所以我得快点更新了,不能拖了😥 文章目录 前言一、打开终端总结 前言 PDF文件被广泛应用于共享信息,电子邮件,网站或文档或存储系统的真实链接 它可以用于恶意软件的载体。 不要问我什么意思&am…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
