qrcode.react生成二维码
-
qrcode.react是一个**用于生成二维码(QR 码)的React组件库。**它提供了一个React组件,可以轻松地在React应用程序中生成和显示QR码。 -
使用
qrcode.react,可以以声明式的方式在React组件中定义QR码的内容、尺寸、颜色等属性,并将其渲染为可交互的二维码图像。该库使用了底层的QR码生成库,以便高效地生成QR码图像。
以下是 qrcode.react 库的一些特点和用法:
- 简单易用:使用 qrcode.react,您只需要在 React 组件中导入并使用 组件即可生成二维码。
- 支持自定义属性:您可以通过传递属性来自定义生成的二维码,例如 value(二维码内容)、size(尺寸)、fgColor(前景色)、bgColor(背景色)等。
- 动态更新:您可以通过更新组件的属性来动态改变生成的二维码,例如根据用户输入的内容动态生成二维码图像。
- 事件处理:qrcode.react 还提供了一些事件处理属性,例如 onError(二维码生成错误时的回调)、onClick(点击二维码时的回调)等,以便您可以对二维码的交互进行处理。
- 响应式支持:您可以使用 CSS 样式和布局技术来使生成的二维码图像具有响应式的特性,以适应不同的屏幕尺寸和设备。
具体用法如下:
import QRCode from 'qrcode.react';<QRCode value={url} size={180} fgColor="#000000" />
相关文章:

qrcode.react生成二维码
qrcode.react 是一个**用于生成二维码(QR 码)的 React 组件库。**它提供了一个 React 组件,可以轻松地在 React 应用程序中生成和显示 QR 码。 使用 qrcode.react,可以以声明式的方式在 React 组件中定义 QR 码的内容、尺寸、颜色…...

ETF套利及交易者如何进行套利的
ETF套利 什么是ETF套利为什么同一ETF在不同交易所上的价格会出现差异?如何操作ETF套利交易所如何解决ETF套利问题的? 什么是ETF套利 ETF(Exchange-Traded Fund)套利是一种通过利用市场中不同交易所交易价格之间的差异来获得利润的…...

了解异或的好处和用途
1.什么是异或? 异或:对于二进制,相同为0 不同为11 ⊕ 1 00 ⊕ 0 01 ⊕ 0 10 ⊕ 1 1 2.异或的好处? 异或的好处?1.快速比较两个值 2.xor a a例如 a 3 011xor 0110003.可以使用 异或 来使某些特定的位翻转【原因…...

vue函数式组件
<template>改为<template functional> 即可然后模板里使用到父组件参数的话,需在变量前面加上 props,如 <div>{{count}}</div> 改为 <div>{{props.count}}</div>如果组件比较简单,只是展示数据的话&…...
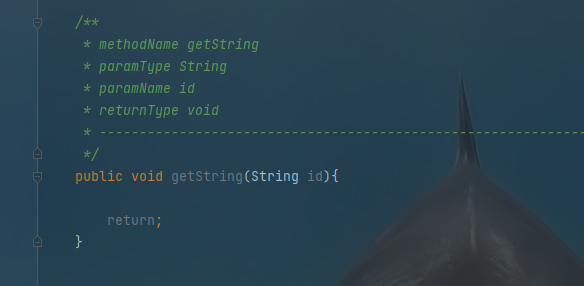
Idea Live Template 功能总结
文章目录 Java自带的template属性模板psf——public static finalpsfi——public static final intpsfi——public static final StringSt——String 方法模板psvm——main方法sout——打印语句iter——for迭代循环fori——for循环 代码块模板if-e —— if elseelse-if 自定义自…...
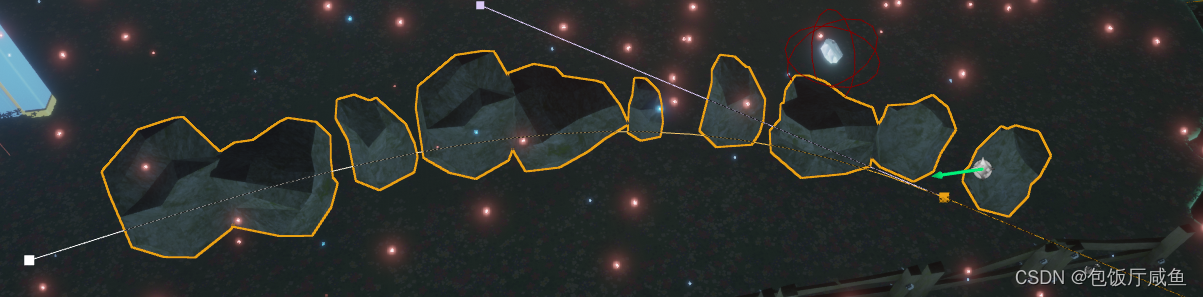
场景入门12----构造脚本搭建栅栏和石头墙
打开任意一个蓝图都有构造脚本,就是当这个蓝图在诞生时就会运行的东西 新建一个蓝图,在构造函数里添加静态网格体,把蓝图拖出来就能显示 多个栅栏 创建多个栅栏。新建一个变量为栅栏数量,数组从0开始,所以countt要减一…...
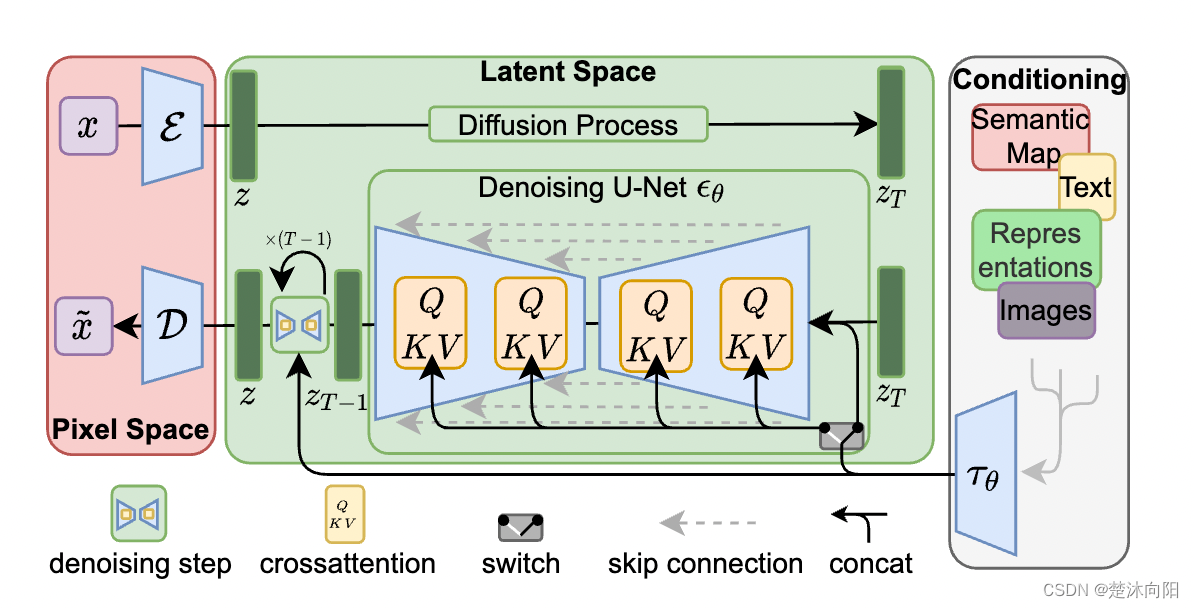
零基础看懂免费开源的Stable Diffusion
文章目录 前言Diffusion模型推理过程训练过程 Stable Diffusion模型参考 前言 前面一篇文章主要讲了扩散模型的理论基础,还没看过上篇的小伙伴可以点击查看:DDPM理论基础。这篇我们主要讲一下一经推出,就火爆全网的Stable Diffusion模型。St…...

Zmq适配Win7 SP0 / Win XP/ Win 2k
1.目的 由于发布版本的libzmq使用了较多新的系统特性,导致在低版本windows平台上无法使用。 因此,需要对zmq源码进行修改以适配低版本的系统,如Win7 SP0,Win XP,Win2003等等。 2.Win7 SP0 #if defined ZMQ_HAVE_WIN…...
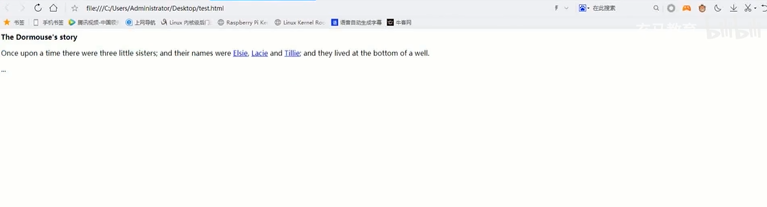
掌握Python的X篇_30_使用python解析网页HTML
本篇将会介绍beutifulsoup4模块,可以用于网络爬虫、解析HTML和XML,对于没有接触过前端,不了解HTML是如何工作的,需要先解释一下什么事HTML。 1. HTML 网页中的各种布局等的背后都是非常简单的纯文本格式,那种格式称为…...
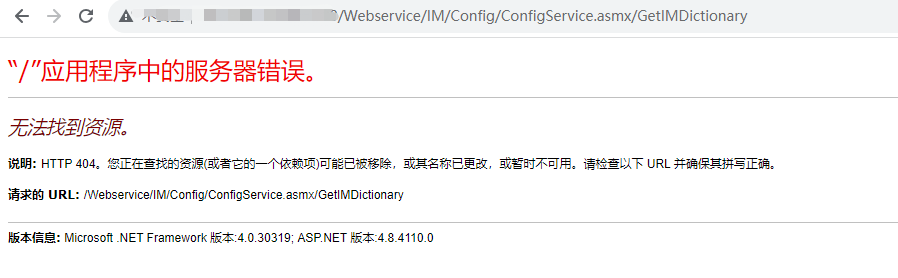
广联达OA前台sql注入+后台文件上传漏洞复现分析
文章目录 前言资产特征前台sql注入后台文件上传解决办法 前言 最近看到广联达OA的前端sql注入和后端文件上传漏洞联动的poc 广联达科技股份有限公司以建设工程领域专业应用为核心基础支撑,提供一百余款基于“端云大数据”产品/服务,提供产业大数据、产业…...
No view found for id 0x7f0901c3 for fragment解决以及线上bug排查技巧
情景再现 开发这么久,不知道你们是否也经历过这样的情况,测试或者用户,反馈app闪退,结果你自己打开开发工具,去调试,一切正常,然后闪退还是存在,只是在开发环境中不能重现。这种情况…...
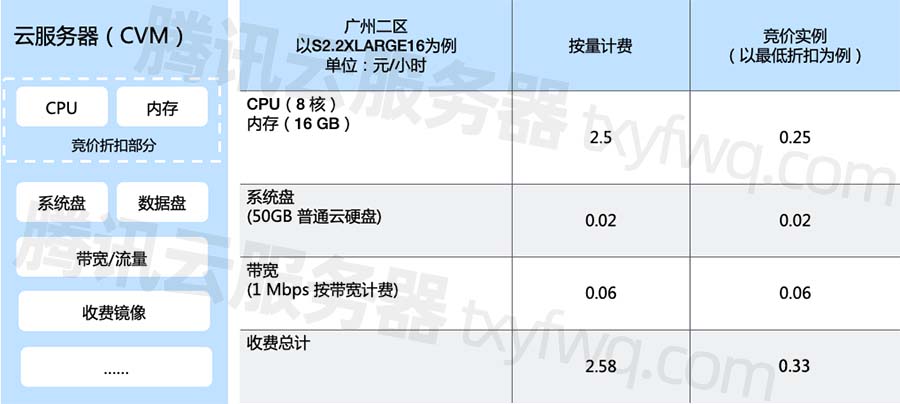
腾讯云CVM服务器竞价实例是什么?和按量计费有什么区别?
腾讯云服务器CVM计费模式分为包年包月、按量计费和竞价实例,什么是竞价实例?竞价实例和按量付费相类似,优势是价格更划算,缺点是云服务器实例有被自动释放风险,腾讯云服务器网来详细说下什么是竞价实例?以及…...

Kali Linux助您网络安全攻防实战
Kali Linux:黑客与防御者的神器 Kali Linux是一款专为网络安全测试和攻防实践而设计的操作系统。它汇集了大量的安全工具,可以用于渗透测试、漏洞扫描、密码破解等任务,不仅为黑客提供了强大的攻击能力,也为安全防御者提供了测试和…...
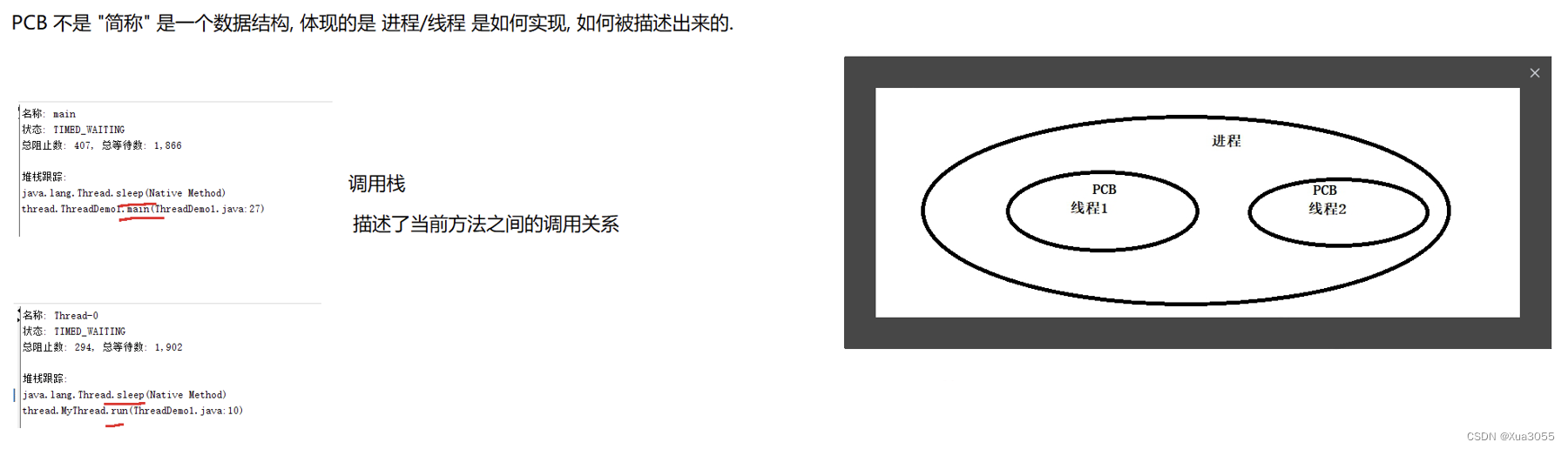
JavaEE初阶:多线程 - 编程
1.认识线程 我们在之前认识了什么是多进程,今天我们来了解线程。 一个线程就是一个 "执行流". 每个线程之间都可以按照顺讯执行自己的代码. 多个线程之间 "同时" 执行 着多份代码. 引入进程这个概念,主要是为了解决并发编程这样的…...
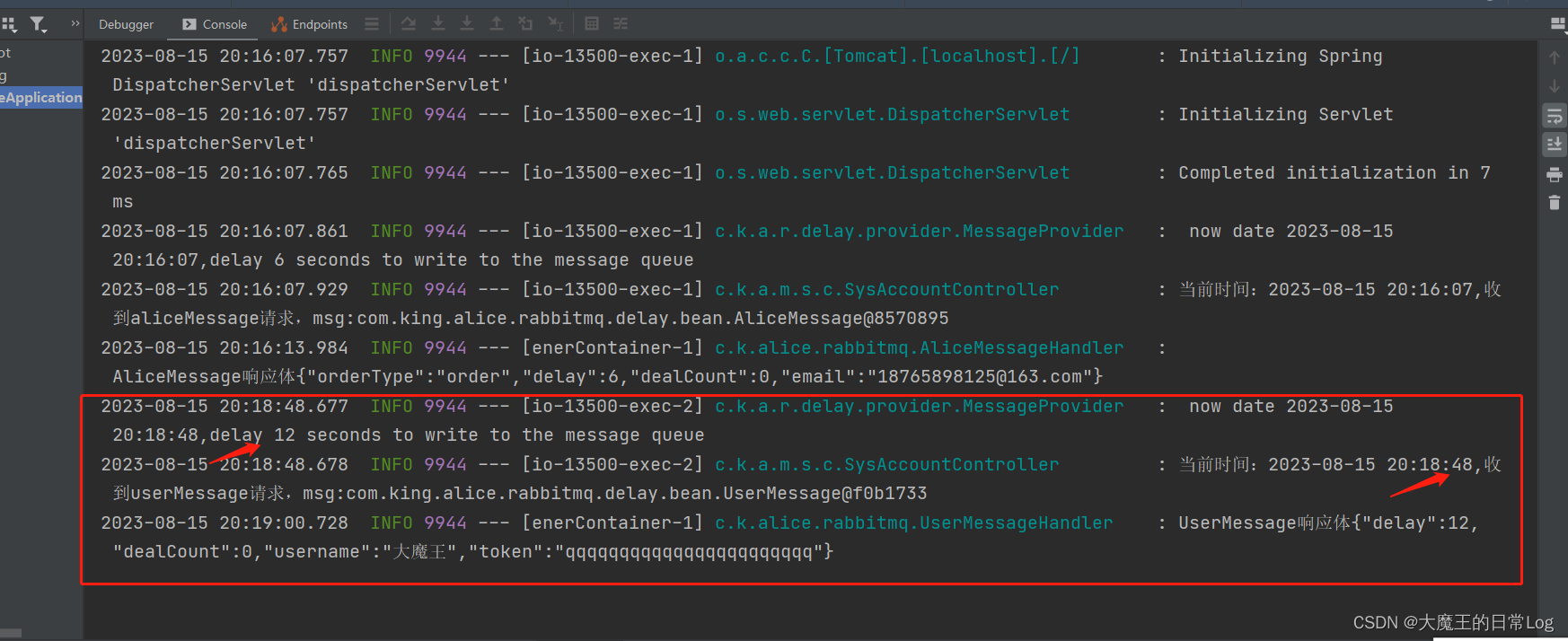
一种多策略下RabbitMQ的延时队列实现
1.为什么会用到延时队列? 场景: 最近在开发一款系统中遇到这样一个场景,A系统开通套餐需要把套餐信息以邮件的形式发送给相关工作人员,经过人工审核通过后,在B系统里面开通,A系统会调B系统套餐列表接口查询套餐是否开通成功,开通成功则从A系统去完成订单,假如超过设定时间未开…...

解密 AI 客服;在不同硬件设备上运行大型语言模型的可能性
🦉 AI新闻 🚀 微软必应首席执行官称必应聊天优于OpenAI的GPT-4,但成本更高 摘要:微软必应的首席执行官米哈伊尔・帕拉欣表示,必应聊天表现优于OpenAI的GPT-4,但使用了更高成本的检索增强推理技术。必应聊…...
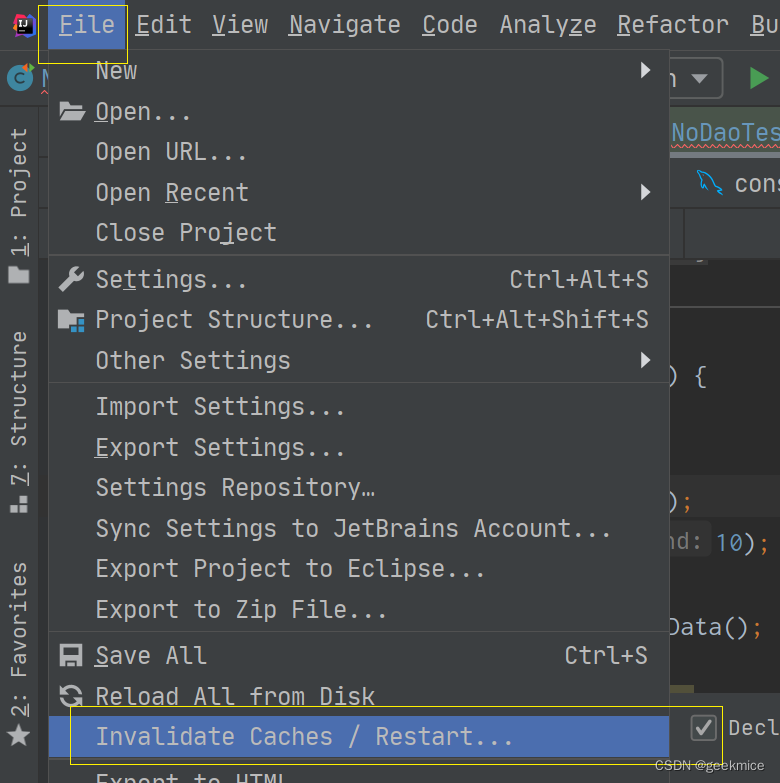
问题:【IntelliJ IDEA】解决idea自动声明变量加finall修饰符问题
问题:【IntelliJ IDEA】解决idea自动声明变量加finall修饰符问题 场景复现 1 new String() 2 快捷方式生成变量 final修饰的 final String s new String();步骤一:确保settings配置信息 settings-----》Editor------》Code Style--------》java下的这两个选项不…...

SpringBoot基于Zookeeper实现分布式锁
文章目录 问题背景前言实现搭建Zookeeper容器引入依赖ZK客户端的配置类ZK客户端的工厂类注入bean构建测试类 问题背景 研究分布式锁,基于ZK实现,需要整合到SpringBoot使用 前言 参考自SpringBoot集成Curator实现Zookeeper基本操作,Zookeeper入…...
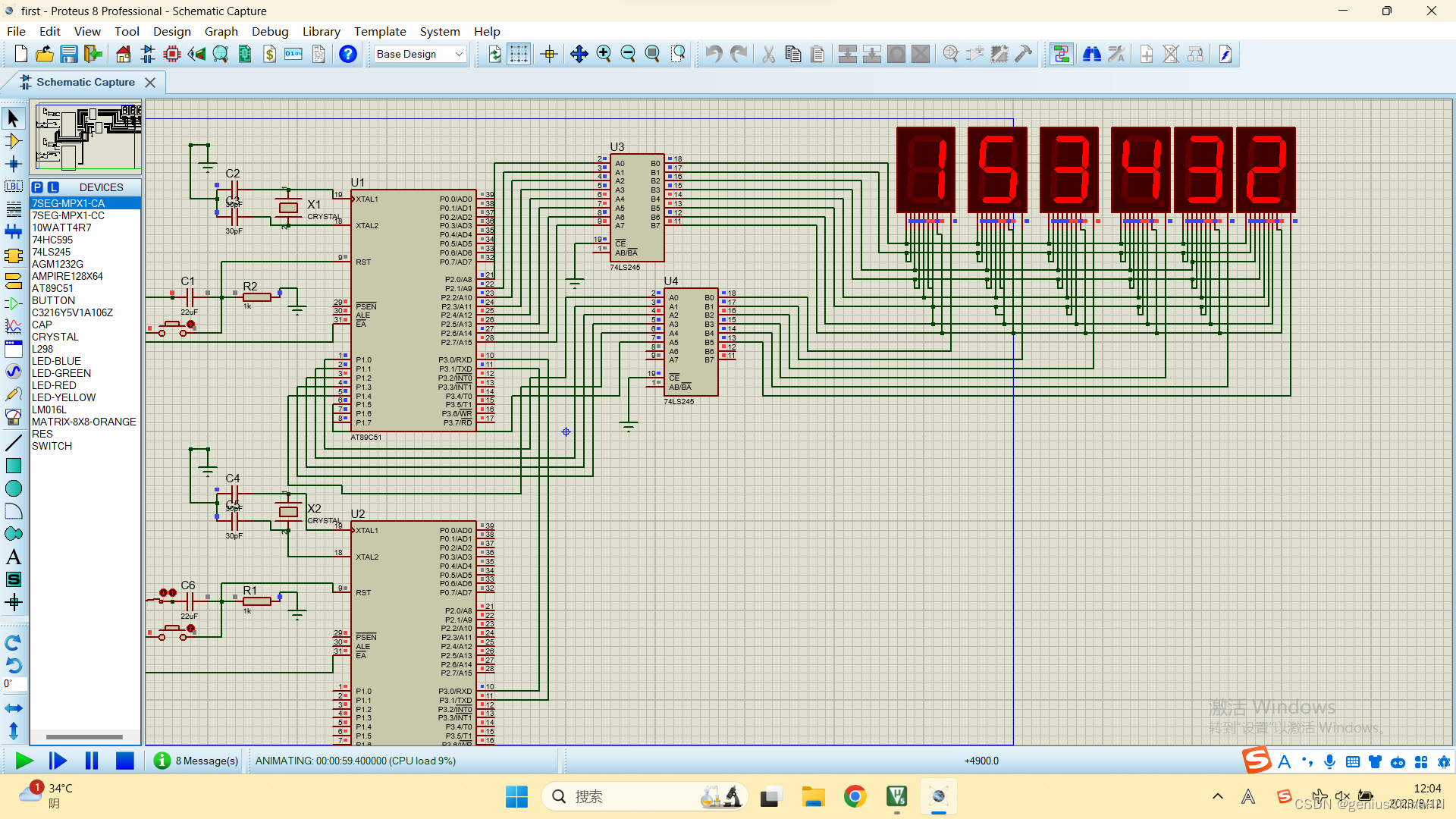
AT89C51单片机实现单片机串口互动(中断方式,单片机--单片机,应答)
说一下功能:客户机发送0x01到服务机 2服务单片机应答0xf2到客户机 3客户机接收到0xf2,发送信息153432这6个数字到服务机 4client发送完信息后发送0xaa结束通信 5server接收到0xaa后回复0xaa结束通信,从此老死不相往来 看代码: //发送端…...

九耶丨阁瑞钛伦特-请说说你在工作中的PRD文档是如何撰写的?
1、背景说明(解释清楚为什么要做这样一件事,以及做这件事的价值,先把观点拉齐,才方便接下来的工作开展) 简要介绍与项目相关的背景信息、项目要满足的用户需求、开展项目的主要原因、项目期望上线时间、项目涉及的具体…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
