浙大数据结构第七周之Saving James Bond - Hard Version
题目详情:
This time let us consider the situation in the movie "Live and Let Die" in which James Bond, the world's most famous spy, was captured by a group of drug dealers. He was sent to a small piece of land at the center of a lake filled with crocodiles. There he performed the most daring action to escape -- he jumped onto the head of the nearest crocodile! Before the animal realized what was happening, James jumped again onto the next big head... Finally he reached the bank before the last crocodile could bite him (actually the stunt man was caught by the big mouth and barely escaped with his extra thick boot).
Assume that the lake is a 100 by 100 square one. Assume that the center of the lake is at (0,0) and the northeast corner at (50,50). The central island is a disk centered at (0,0) with the diameter of 15. A number of crocodiles are in the lake at various positions. Given the coordinates of each crocodile and the distance that James could jump, you must tell him a shortest path to reach one of the banks. The length of a path is the number of jumps that James has to make.
Input Specification:
Each input file contains one test case. Each case starts with a line containing two positive integers N (≤100), the number of crocodiles, and D, the maximum distance that James could jump. Then N lines follow, each containing the (x,y) location of a crocodile. Note that no two crocodiles are staying at the same position.
Output Specification:
For each test case, if James can escape, output in one line the minimum number of jumps he must make. Then starting from the next line, output the position (x,y) of each crocodile on the path, each pair in one line, from the island to the bank. If it is impossible for James to escape that way, simply give him 0 as the number of jumps. If there are many shortest paths, just output the one with the minimum first jump, which is guaranteed to be unique.
Sample Input 1:
17 15
10 -21
10 21
-40 10
30 -50
20 40
35 10
0 -10
-25 22
40 -40
-30 30
-10 22
0 11
25 21
25 10
10 10
10 35
-30 10
Sample Output 1:
4
0 11
10 21
10 35
Sample Input 2:
4 13
-12 12
12 12
-12 -12
12 -12
Sample Output 2:
0简单翻译:
相比于简单版本,要求找到最短路
主要思路:
麻了,搞了一星期,在Dijkstra和BFS反复横跳,最后其实是BFS + Dijkstra的组合拳模式解决
设置path[n](path[i]表示节点i的上一级节点),这样可以利用堆栈回溯
(一):数据初始化,将读入的鳄鱼按从近到远排序
(二):构建图
第一次写错误:
代码实现:
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>const int INF = 0x3f3f3f3f;struct Point {int x, y;
};int jumpDist(Point *point, int pos1, int pos2);
int findSrc(int *path, int pos);
int srcDist(Point *point, int pos);
int BFS(Point *point, int *path, int n, int r);int main() {int n, r;scanf("%d %d", &n, &r);Point point[n];for (int i = 0; i < n; i++) {scanf("%d %d", &point[i].x, &point[i].y);}if (7.5 + r >= 50) { // 如果一步就可以跳到边界,直接输出1即可。最后一个测试点会卡这种情况printf("1\n");}else {int path[n]; // 数组的下标对应点的编号,用来记录该点的前一个点的编号std::fill(path, path + n, -1); // 初始化为-1代表没有点可以跳跃到该点int minId = BFS(point, path, n, r); // 调用上述的BFS,返回的是跳跃的最后一个点的数组下标位置if (minId == -1) { // 如果返回-1说明找不到可以到达边界的路线printf("0\n");}else {std::stack<int> s;for (int i = minId; i != -1; i = path[i]) {s.push(i); // 把整个跳跃过程经过的点的下标位置压入栈中,压的顺序是从终点到始点}printf("%d\n", s.size() + 1);while (!s.empty()) {int i = s.top(); // 把每个点的下标位置弹出来,打印的顺序是从始点到终点s.pop();printf("%d %d\n", point[i].x, point[i].y);}}}return 0;
}// 用来计算两个点的欧氏距离的平方
int jumpDist(Point *point, int pos1, int pos2) {return (point[pos1].x - point[pos2].x) * (point[pos1].x - point[pos2].x) + (point[pos1].y - point[pos2].y) * (point[pos1].y - point[pos2].y);
}// 用来找到经过该点的路径的始点
int findSrc(int *path, int pos) {return path[pos] == -1 ? pos : findSrc(path, path[pos]);
}// 用来计算该点与原点(0, 0)的欧氏距离的平方
int srcDist(Point *point, int pos) {return point[pos].x * point[pos].x + point[pos].y * point[pos].y;
}int BFS(Point *point, int *path, int n, int r) {int dist[n], minId = -1, minDist = INF; // minDist用来记录最小的跳跃次数,minId用来记录最小跳跃次数对应的那条路线的最后一个点std::fill(dist, dist + n, INF);std::queue<int> q;for (int i = 0; i < n; i++) {int d = srcDist(point, i);if (d > 7.5 * 7.5 && d <= (7.5 + r) * (7.5 + r)) { // 如果该点不再给定的原点范围内,并且可以从原点范围跳跃到该点q.push(i); // 就把该点压入队列中dist[i] = 1; // 同时到该点的跳跃次数+1}}while (!q.empty()) { // 队列不为空int tmp = q.front();q.pop();for (int i = 0; i < n; i++) {int d = jumpDist(point, tmp, i);// 如果不可以跳跃到这个点,或者这条鳄鱼在岛上,忽略这个点,走下一次的循环if (d > r * r || srcDist(point, i) <= 7.5 * 7.5) continue;//经过上面语句筛选后下来的节点都是可以跳到且不在岛上的节点//下面这个if语句用了Dijkstra思想if (dist[tmp] + 1 < dist[i]) { // 如果从原点经过tmp跳跃到该点的次数比之前直接从原点跳跃到该点的跳跃次数小dist[i] = dist[tmp] + 1; // 更新为更小的跳跃次数path[i] = tmp; // 同时把到该点点的前一个节点更新为tmpq.push(i); // 把该点压入队列}if (50 - abs(point[i].x) <= r || 50 - abs(point[i].y) <= r) { // 如果可以从该点跳跃到边界if (minDist > dist[i]) { // 到该点的跳跃次数比之前记录的最小跳跃次数小minDist = dist[i]; // 更新最小跳跃次数minId = i; // 更新对应路径的最后一个点}else if (minDist == dist[i]) { // 如果最小的跳跃次数相同int src1 = findSrc(path, minId); // 找到minId对应路径的的始点int src2 = findSrc(path, i); // 找到该点对应路径的始点if (srcDist(point, src2) < srcDist(point, src1)) minId = i; // 如果该点对应路径的始点到原点的距离更小,更新minId}}}}return minId;
}有问题的代码:
排过序,用Dijkstra
/*
建图
图的权值
最短路
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define MAX_NODE_NUMS 105
#define INFINITY 1005
#define RADIUS 7.5
#define BOUNDRY 50
#define FALSE 0
#define TRUE 1
#define NONE -1
typedef int bool;
typedef struct MatrixGrapbNode MatrixGrapbNode;
typedef MatrixGrapbNode* MGraph;
struct MatrixGrapbNode {int VertexNums, EdgeNums;int Weight[MAX_NODE_NUMS][MAX_NODE_NUMS];
};
/*建图,难点是如何判断在两个节点之间插入边*/
MGraph CreateEmptyGraph(int vertexNums) {MGraph graph = (MGraph)malloc(sizeof(MatrixGrapbNode));graph->VertexNums = vertexNums;for(int i = 0; i < vertexNums; i++) {for(int j = 0; j < vertexNums; j++) {if(i == j) {graph->Weight[i][j] = FALSE;}else {graph->Weight[i][j] = INFINITY;}}}return graph;
}
void InsertEdge(int start, int end, int weight, MGraph graph) {graph->Weight[start][end] = weight;graph->Weight[end][start] = weight;return;
}
typedef struct Node Node;
struct Node {int xLabel, yLabel;
};
Node node[MAX_NODE_NUMS];
int DistanceSquare(int difX, int difY) {return pow(difX, 2) + pow(difY, 2);
}
bool CanJump(int start, int end, int jumpDistance, int vertexNums) {bool flag = FALSE;int x1 = node[start].xLabel; int y1 = node[start].yLabel;int x2 = node[end].xLabel; int y2 = node[end].yLabel;int difX = x1 - x2; int difY = y1 - y2;if(start == 0 || end == 0) {if(DistanceSquare(difX, difY) <= pow(RADIUS + jumpDistance, 2)) {flag = TRUE;}}else if(start == vertexNums - 1 || end == vertexNums - 1) {if(abs(difX) <= jumpDistance || abs(difY) <= jumpDistance) {flag = TRUE;}}else {if(DistanceSquare(difX, difY) <= pow(jumpDistance, 2)) {flag = TRUE;}}return flag;
}
void Swap(Node* a, Node* b) {Node temp = *a;*a = *b;*b = temp;return;
}
void Sort(MGraph graph) {for(int i = 1; i < graph->VertexNums - 1; i++) {for(int j = i + 1; j < graph->VertexNums - 1; j++) {int distanceSquare1ToCenter = DistanceSquare(node[i].xLabel, node[i].yLabel);int distanceSquare2ToCenter = DistanceSquare(node[j].xLabel, node[j].yLabel);if(distanceSquare1ToCenter > distanceSquare2ToCenter) {Swap(&node[i], &node[j]);}}}
}
MGraph BuildGraph(int crocodileNums, int jumpDistance) {int vertexNums = crocodileNums + 2;MGraph graph = CreateEmptyGraph(vertexNums);//node[0].xLabel = 0; node[0].yLabel = 0;node[vertexNums - 1].xLabel = BOUNDRY; node[vertexNums - 1].yLabel = BOUNDRY;for(int i = 1; i <= crocodileNums; i++) {scanf("%d %d", &(node[i].xLabel), &(node[i].yLabel));}Sort(graph);for(int i = 0; i < vertexNums; i++) {for(int j = 0; j < vertexNums; j++) {if(CanJump(i, j, jumpDistance, vertexNums)) {InsertEdge(i, j, TRUE, graph);}}}return graph;
}
int FindNearest(MGraph graph, int dis[], int collected[]) {int minDis = INFINITY;int nearestNode = NONE;for(int i = 0; i < graph->VertexNums; i++) {if(collected[i] == FALSE && dis[i] < minDis) {minDis = dis[i];nearestNode = i;}}return nearestNode;
}
/*dikstra寻找最短路*/
void Dikistra(MGraph graph, int start) {int path[graph->VertexNums]; //path[i]记录的是节点i的上一级节点int dis[graph->VertexNums]; //dis[i]记录的是从起点到节点i的距离int collected[graph->VertexNums]; //collected[i]记录的是当前节点i有没有访问过/*初始化*/for(int i = 0; i < graph->VertexNums; i++) {dis[i] = graph->Weight[start][i];if(dis[i] < INFINITY) {path[i] = start;}else {path[i] = NONE;}collected[i] = FALSE;}//先将起点放入集合dis[start] = 0;collected[start] = TRUE;while(TRUE) {int nearest = FindNearest(graph, dis, collected);if(nearest == NONE) {break;}collected[nearest] = TRUE;for(int i = 0; i < graph->VertexNums; i++) {if(collected[i] == FALSE && graph->Weight[nearest][i] < INFINITY) {if(graph->Weight[nearest][i] < 0) {printf("%d", FALSE);return;}if(dis[nearest] + graph->Weight[nearest][i] < dis[i]) {dis[i] = dis[nearest] + graph->Weight[nearest][i];path[i] = nearest;}}}}if(path[graph->VertexNums - 1] != NONE) {int shortestDistance = dis[graph->VertexNums - 1]; printf("%d\n", shortestDistance);Node* shortestWay[shortestDistance];for(int i = 0; i < shortestDistance; i++) {shortestWay[i] = NULL;} int count = shortestDistance; //当前还剩的节点数量int pathIndex = graph->VertexNums - 1; //指向path的指针int shortestWayIndex = shortestDistance - 1; //指向shortestWay的指针int parent = NONE;while(count) {shortestWay[count - 1] = &(node[pathIndex]); pathIndex = path[pathIndex];count--;}for(int i = 0; i < shortestDistance - 1; i++) {printf("%d %d\n", shortestWay[i]->xLabel, shortestWay[i]->yLabel);}} else {printf("%d", FALSE);}return;
}
int main() {int crocodileNums, jumpDistance;scanf("%d %d", &crocodileNums, &jumpDistance);MGraph graph = BuildGraph(crocodileNums, jumpDistance);Dikistra(graph, 0);free(graph);return 0;
}相关文章:

浙大数据结构第七周之Saving James Bond - Hard Version
题目详情: This time let us consider the situation in the movie "Live and Let Die" in which James Bond, the worlds most famous spy, was captured by a group of drug dealers. He was sent to a small piece of land at the center of a lake f…...

线程同步条件变量
为何要线程同步 在线程互斥中外面解决了多线程访问共享资源所会造成的问题。 这篇文章主要是解决当多线程互斥后引发的新的问题:线程饥饿的问题。 什么是线程饥饿?互斥导致了多线程对临界区访问只能改变为串行,这样访问临界资源的代码只能…...
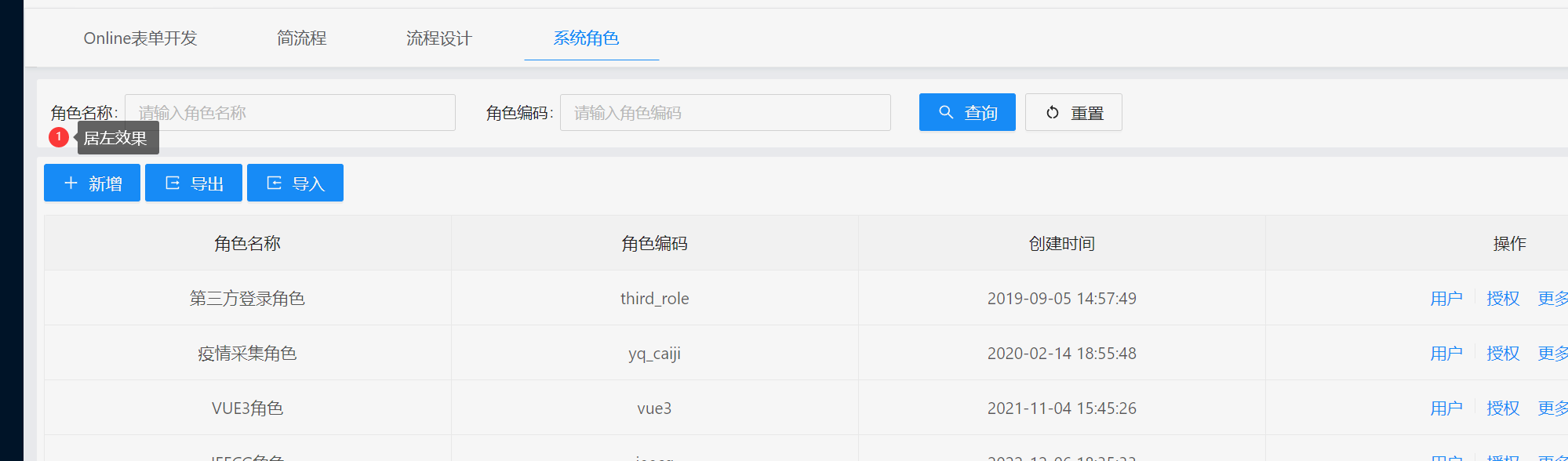
jeecgboot-vue3 查询区 label 文字居左实现
以系统管理中的系统角色界面为例 操作步骤 1. 通过路由或者工具找到当前代码所在的文件 src/views/system/role/index.vue 2. 找到 useListPage 调用,fromConfig 对象加入 labelWidth 和 rowProps 属性 formConfig: {labelWidth: 65, // 设置所有的label宽rowPr…...
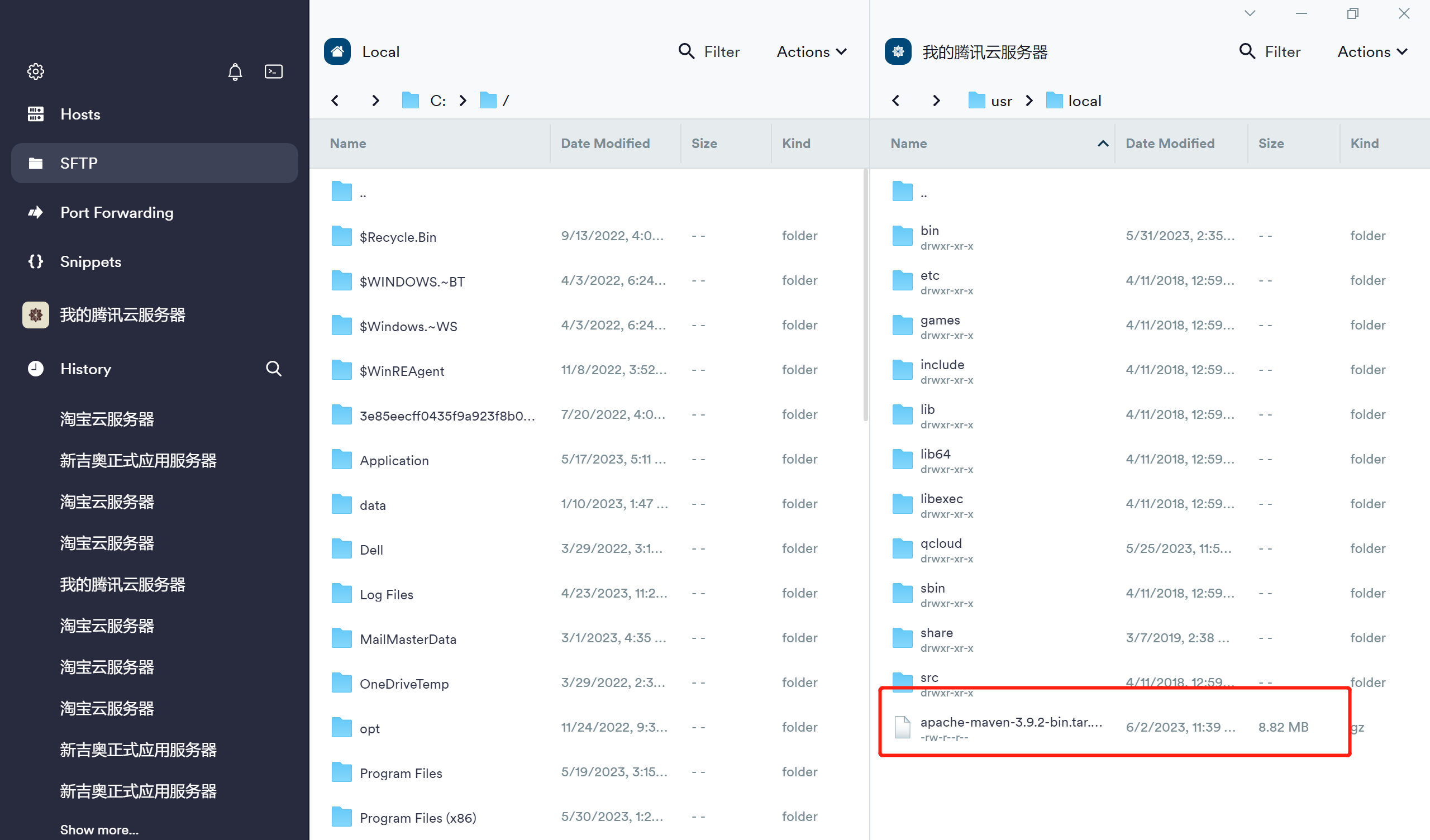
CentOS系统环境搭建(五)——Centos7安装maven
centos系统环境搭建专栏🔗点击跳转 Centos7安装maven 下载压缩包 maven下载官网 解压 压缩包放置到/usr/local tar -xvf apache-maven-3.9.2-bin.tar.gz配置环境变量 vim /etc/profile在最下面追加 MAVEN_HOME/usr/local/apache-maven-3.9.2 export PATH${MAV…...

.eslintrc配置
ESLint 标准规则 /*** AlloyTeam ESLint 规则** 包含所有 ESLint 规则* 使用 babel-eslint 作为解析器** fixable 表示此配置支持 --fix* off 表示此配置被关闭了,并且后面说明了关闭的原因*/module.exports {parser: babel-eslint,parserOptions: {ecmaVersion: 2…...
LangChain手记 Models,Prompts and Parsers
整理并翻译自DeepLearning.AILangChain的官方课程:Models,Prompts and Parsers(源码可见) 模型,提示词和解析器(Models, Prompts and Parsers) 模型:大语言模型提示词:构建传递给模…...

Cannot resolve plugin ... maven插件和依赖无法下载解决方法
将 maven/conf/settings.xml 配置文件中的mirror修改成如下即可 <?xml version"1.0" encoding"UTF-8"?> <settings xmlns"http://maven.apache.org/SETTINGS/1.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"…...

【skynet】skynet 服务间通信
写在前面 skynet 服务之间有自己的一套高效通信 API 。本文给出简单的示例。 文章目录 写在前面准备工作编写代码运行结果 准备工作 首先要有一个编译好,而且工作正常的 skynet 。 编写代码 在 skynet/example 目录编写一个配置文件,两个代码文件。 …...
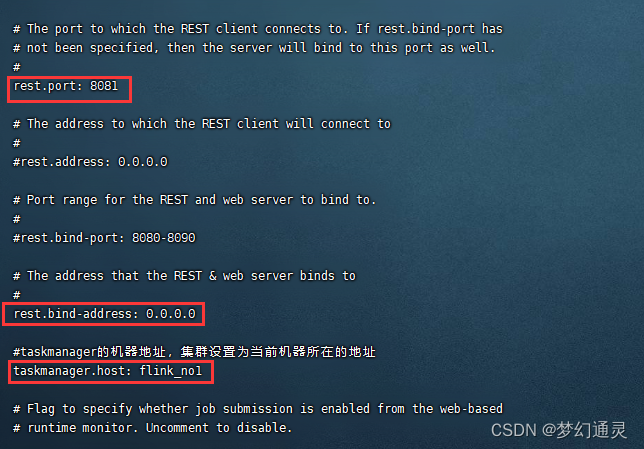
Flink的Standalone部署实战
在Flink是通用的框架,以混合和匹配的方式支持部署不同场景,而Standalone单机部署方便快速部署,记录本地部署过程,方便备查。 环境要求 1)JDK1.8及以上 2)flink-1.14.3 3)CentOS7 Flink相关信…...
像素的操作)
open cv学习 (一)像素的操作
open cv 入门 像素的操作 demo1 import cv2 import os import numpy as np# 1、读取图像 # imread()方法# 设置图像的路径 Path "./img.png" # 设置读取颜色类型默认是1代表彩色图 0 代表灰度图 # 彩色图 flag 1 # 灰度图 #flag 0# 读取图像,返回值…...
基于C#的消息处理的应用程序 - 开源研究系列文章
今天讲讲基于C#里的基于消息处理的应用程序的一个例子。 我们知道,Windows操作系统的程序是基于消息处理的。也就是说,程序接收到消息代码定义,然后根据消息代码定义去处理对应的操作。前面有一个博文例子( C#程序的启动显示方案(无窗口进程发…...
C语言刷题指南(一)
📙作者简介: 清水加冰,目前大二在读,正在学习C/C、Python、操作系统、数据库等。 📘相关专栏:C语言初阶、C语言进阶、数据结构刷题训练营、有感兴趣的可以看一看。 欢迎点赞 👍 收藏 ⭐留言 &am…...
VMware虚拟机Ubuntu无法连接网络的解决方法
一、解决办法 网络适配器设置 终端依次执行下面命令即可 sudo nmcli networking off sudo nmcli networking onsudo service network-manager start #或者 sudo service NetworkManager start成功出现这个图标,即代表网络连接成功。...
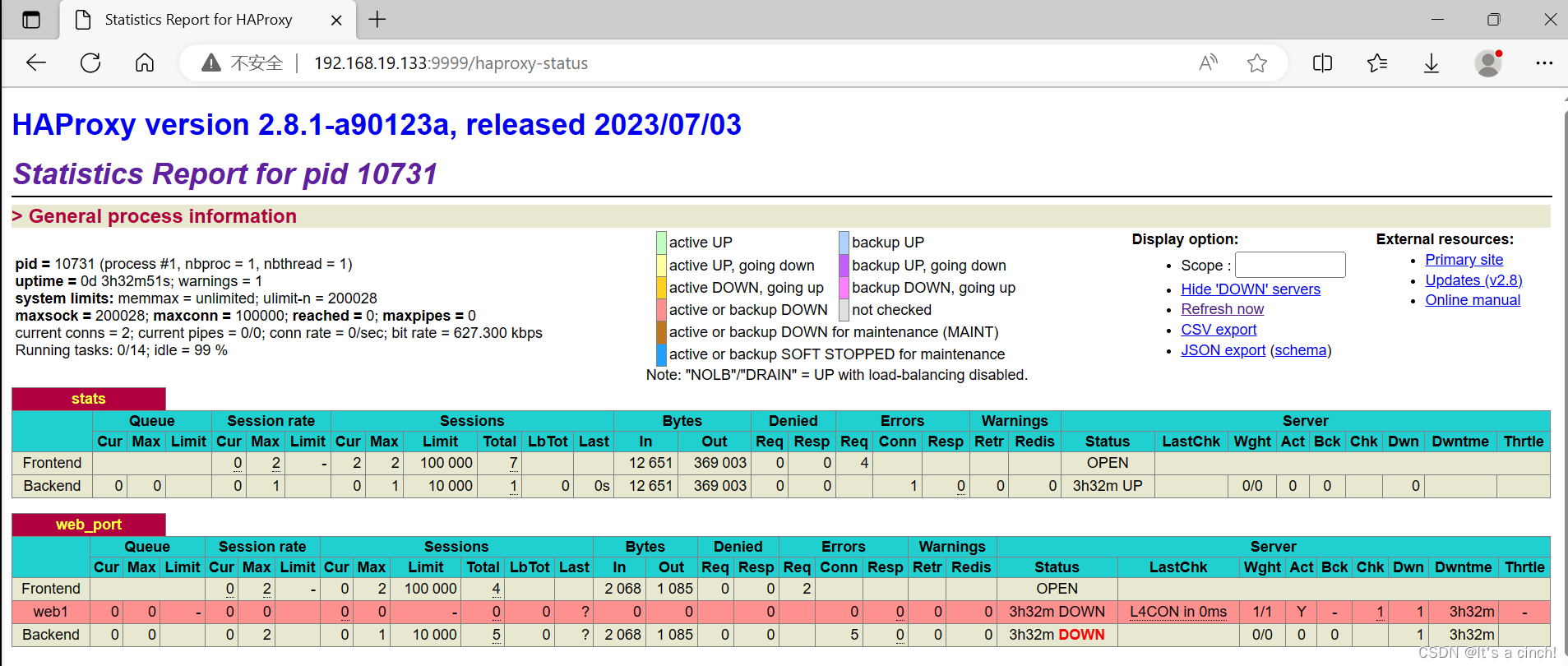
基于CentOS 7 部署社区版Haproxy
HAProxy是法国开发者 威利塔罗(Willy Tarreau) 在2000年使用C语言开发的一个开源软件,是一款具 备高并发(一万以上)、高性能的TCP和HTTP负载均衡器,支持基于cookie的持久性,自动故障切换,支 持正则表达式及web状态统计。 目录 1…...
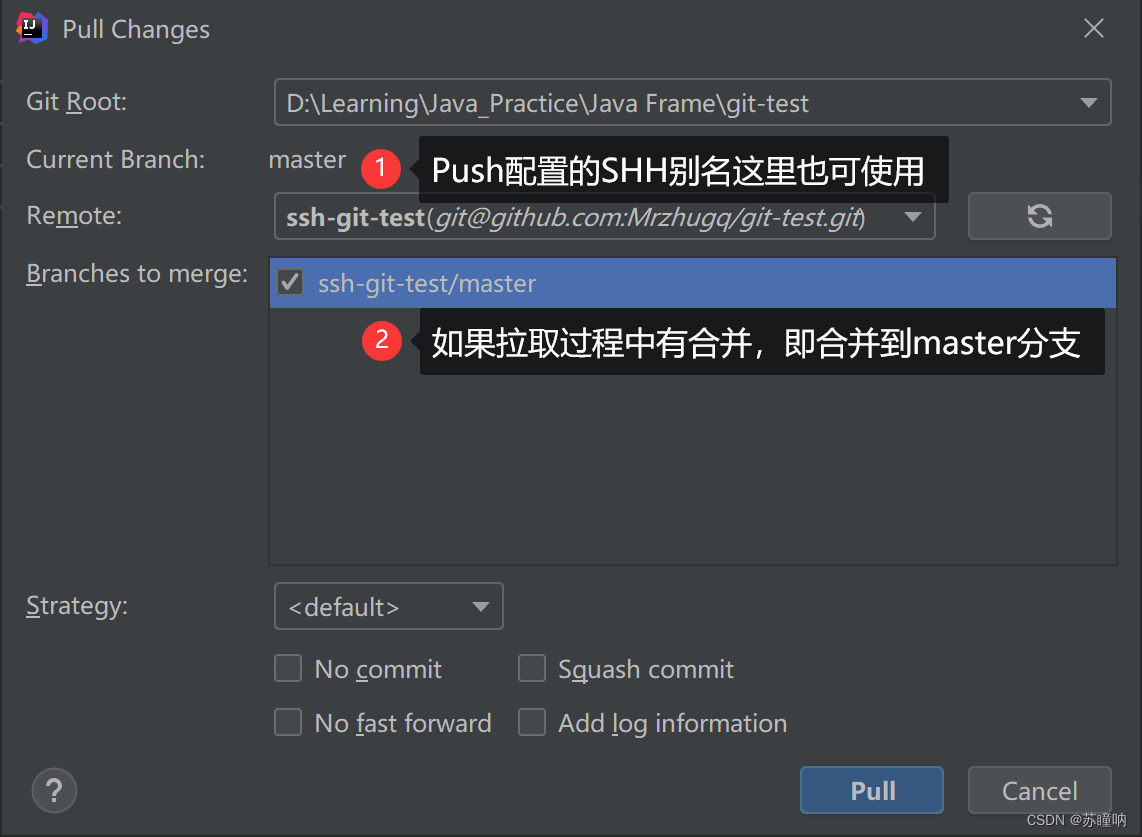
Git和GitHub
文章目录 1.Git介绍2. 常用命令3. Git分支操作4. Git团队协作机制5. GitHub操作6. IDEA集成Git7.IDEA操作GitHub8. Gitee 1.Git介绍 Git免费的开源的分布式版本控制系统,可以快速高效从小到大的各种项目 Git易于学习,占地面积小,性能快。它…...

spring入门基本介绍及注入方式---详细介绍
一,spring的简介 Spring是一个开源框架,它由Rod Johnson创建。它是为了解决企业应用开发的复杂性而创建的。 提供了许多功能强大且易于使用的特性,使得开发者能够更加轻松地构建可维护且可扩展的应用程序,简单来说: Spring使用基…...

神经网络基础-神经网络补充概念-24-随机初始化
由来 在神经网络的训练过程中,权重和偏差的初始值对模型的性能和训练过程的收敛速度都有影响。随机初始化是一种常用的权重和偏差初始值设置方法,它有助于打破对称性,避免网络陷入局部最优解。 概念 当所有权重和偏差都被设置为相同的初始…...
K8S之存储卷
K8S之存储卷 一、emptyDir emptyDir:可实现Pod中的容器之间共享目录数据,但emptyDir存储卷没有持久化数据的能力,存储卷会随着Pod生命周期结束而一起删除二、hostPath hostPath:将Node节点上的目录/文件挂载到Pod容器的指定目录…...

8月17日,每日信息差
1、专家称无需太过担心EG.5变异株 2、快手职级体系调整,职级序列由双轨变单轨 3、抖音、火山引擎、中国电影资料馆发起“经典香港电影修复计划”,一年内将100部香港电影修复至4K版本。本次修复工作由火山引擎提供技术支持,与中国电影资料馆…...

VBA技术资料MF44:VBA_把数据从剪贴板粘贴到Excel
【分享成果,随喜正能量】人皆知以食愈饥,莫知以学愈愚,生命中所有的不期而遇都是你努力的惊喜.人越纯粹,就越能感受到美。大江、大河、大海、大山、大自然,这些风景从来都不会受“属于谁”的污染,人人都感受到它们的美…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...
