算法导论【分治思想】—大数乘法、矩阵相乘、残缺棋盘
这里写自定义目录标题
- 分治法概述
- 特点
- 大数相乘问题
- 分治算法
- 矩阵相乘
- 分治算法
- 残缺棋盘
- 分治算法
分治法概述
在分而治之的方法中,一个问题被划分为较小的问题,然后较小的问题被独立地解决,最后较小问题的解决方案被组合成一个大问题的解决。
通常,分治算法有三个部分:
- 分解:将问题划分为若干子问题,这些子问题是同一问题的较小实例。
- 解决:通过递归地解决子问题来征服它们。如果它们足够小,则将子问题作为基本情况解决。
- 合并:将子问题的解决方案合并为原始问题的解决方法。
特点
分治方法支持并行性,因为子问题是独立的。因此,使用该技术设计的算法可以在多处理器系统上或在不同的机器上同时运行。在这种方法中,大多数算法都是使用递归设计的,因此内存管理非常高。对于递归函数堆栈,需要存储函数状态。
大数相乘问题
-
输入:两个n位整数X和Y。
-
输出:X和Y的乘积。
-
示例:X=1980 Y=2315
-

-
这是你在小学学的算法。注意这需要O(n2) 时间
分治算法
-
按如下方式分解XY,得到一个新的计算公式,但这个公式仍然要计算:ac、ad、bc、bd四个乘式

-
因此它的递归式为:

-
运用主方法可以求出,递归式的解为T(n)=O(n2)。与原始方法相比,该方法没有显著改进。为了减少时间复杂性,我们必须减少乘法次数
-
修改计算公式如下:

-
最后两个XY乘法方案的复杂度为O(nlog3),但考虑到a+b,c+d可能得到n+1位的结果,这使得问题的规模更大,因此没有选择第三个方案。
-
可以列出如下递归式:

-
解得T(n)=O(nlog3)=O(n1.59)。
矩阵相乘
- 让我们考虑两个矩阵A和B。我们想通过乘以A和B来计算得到的矩阵C。
- 朴素方法是如果A=(aij)和B=(bij)是n×n的矩阵,那么在乘积C=A·B中,我们定义条目cij,对于i,j=1,2,。。。,n、 通过cij=∑k=1naik⋅bkjcij=\sum^n_{k=1}a_{ik}·b_{kj}cij=∑k=1naik⋅bkj。
- 我们必须计算n2个矩阵条目,每个条目都是n个值的总和。
- 我们假设整数运算需要O(1)时间。该算法中有三个for循环,一个嵌套在另一个循环中。因此,该算法需要O(n3)时间来执行

分治算法
下面是两个方阵相乘的简单除法。
- 将矩阵A和B分成4个子矩阵,大小为N/2×N/2,如下图所示。
- 递归计算以下值

- 在上述方法中,我们对大小为N/2×N/2的矩阵进行了8次乘法运算和4次加法运算。两个矩阵相加需要O(n2) 时间。因此,时间复杂度为T(n)= 8T(n/2)+O(n2) 。根据主定理,上述方法的时间复杂度为 O(n3),不幸的是,这与上述朴素方法相同。简单的分治也会导致O(n3),有更好的方法吗?
- 在上述分治的方法中,高时间复杂度的主要组成部分是8个递归调用。Strassens方法的思想是将递归调用的数量减少到7。Strassens方法与上述简单除法和征服法相似,因为该方法也将矩阵划分为大小为N/2×N/2的子矩阵,如上图所示,但在Strassens法中,使用以下公式计算结果的四个子矩阵。
- Strassen算法定义了新的矩阵

- 仅使用7次乘法(对每个MkM_kMk)而不是8次。我们现在可以用Mk表示Ci:

- 两个矩阵的加法和减法需要O(n2)时间。因此,时间复杂性可以写成:

- 根据主定理,上述方法的时间复杂度为O(nlog7),近似于O(n2.8074)
-
Hopcroft和Kerr证明(1971)在两个2×2矩阵的乘法中需要7次乘法。因此,为了进一步提高矩阵乘法复杂度的时间,它不能再基于计算2×2矩阵的7倍乘法的方法。也许应该研究3×3或5×5矩阵的更好算法。目前,最佳计算时间上限为O(n 2.376)。
残缺棋盘
- 定义:有缺陷的棋盘是一块2k×2k的正方形棋盘,正好有一个有缺陷的正方形
- 例子:

- 要求用一种化合物来平铺(覆盖)所有非残缺方格。
- 化合物是一种L形物体,可以覆盖棋盘的三个方格。
- 有四个方向:

分治算法
- 分成四个小棋盘。
- 其中一个是有缺陷的棋盘。

- 通过在其他三个棋盘的共同角落放置一个三分之一,使其有缺陷。
- 递归平铺四个有缺陷的棋盘

- 设n=2k,d是常数。 设t(k)是平铺2k×2k有缺陷棋盘所花费的时间。然后

- 这里,c是常数,表示为化合物找到合适位置和旋转化合物以获得所需形状所花费的时间。

- 由于每个网格必须花费θ(1)时间来放置每个化合物,因此不可能得到一个更快的算法来解决这个问题
相关文章:

算法导论【分治思想】—大数乘法、矩阵相乘、残缺棋盘
这里写自定义目录标题分治法概述特点大数相乘问题分治算法矩阵相乘分治算法残缺棋盘分治算法分治法概述 在分而治之的方法中,一个问题被划分为较小的问题,然后较小的问题被独立地解决,最后较小问题的解决方案被组合成一个大问题的解决。 通常…...
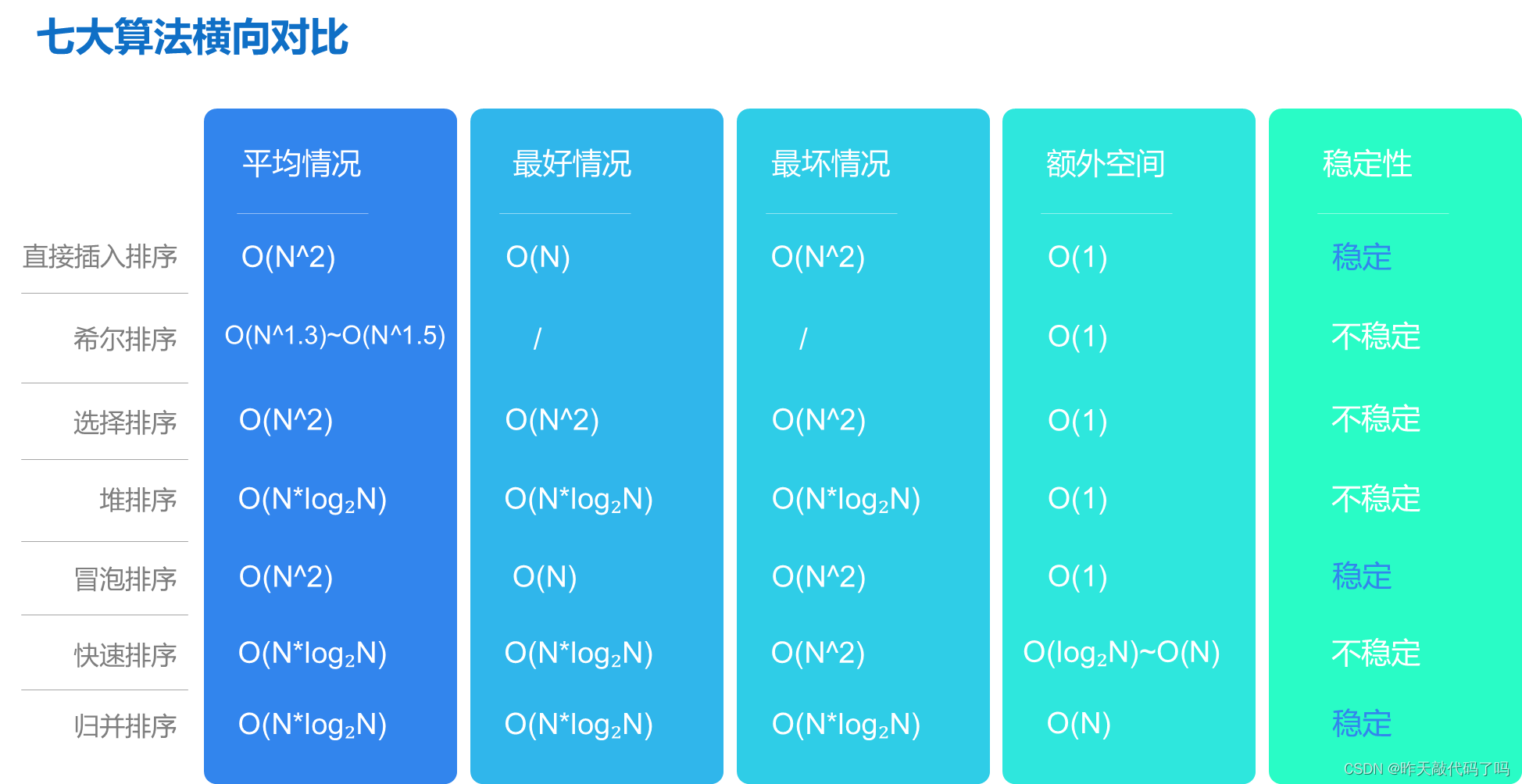
Java【七大排序】算法详细图解,一篇文章吃透
文章目录一、排序相关概念二、七大排序1,直接插入排序2,希尔排序3,选择排序4,堆排序5,冒泡排序5.1冒泡排序的优化6,快速排序6.1 快速排序的优化7,归并排序三、排序算法总体分析对比总结提示&…...

Autosar OS IOC
Inter-OS-Application Communicator 背景和基本原理General purposeIOC functionalityCommunicationNotificationIOC interface背景和基本原理 The IOC implementation shall be part of the Operating System IOC和操作系统紧密相关,是操作系统实现的一部分 The IO…...
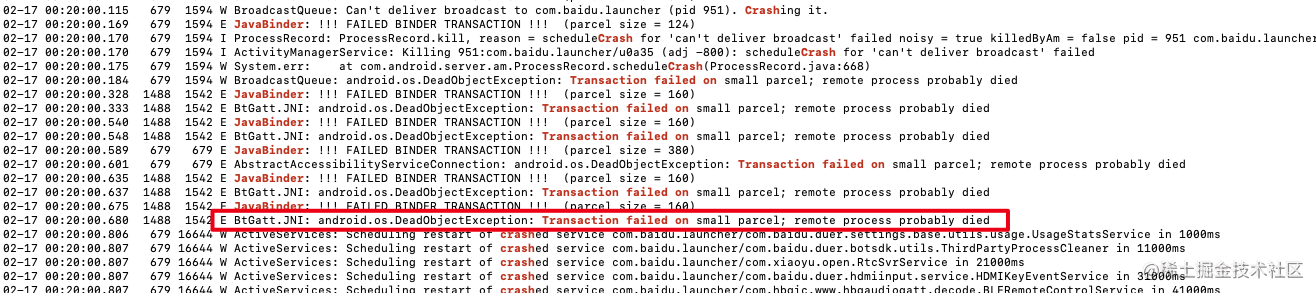
记录一次Binder内存相关的问题导致APP被杀的BUG排查过程
事情的起因的QA压测过程发生进程号变更,怀疑APP被杀掉过,于是开始看日志 APP的压测平台会上报进程号变更时间点,发现是在临晨12:20分,先大概确定在哪个日志文件去找关键信息一开始怀疑是crash,然后就在日志…...
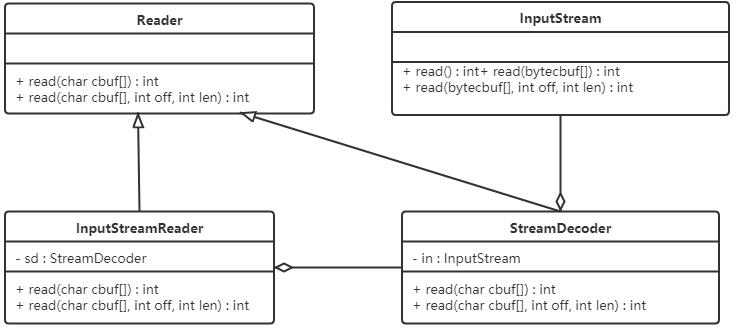
设计模式(十)----结构型模式之适配器模式
1、概述 如果去欧洲国家去旅游的话,他们的插座如下图最左边,是欧洲标准。而我们使用的插头如下图最右边的。因此我们的笔记本电脑,手机在当地不能直接充电。所以就需要一个插座转换器,转换器第1面插入当地的插座,第2面…...
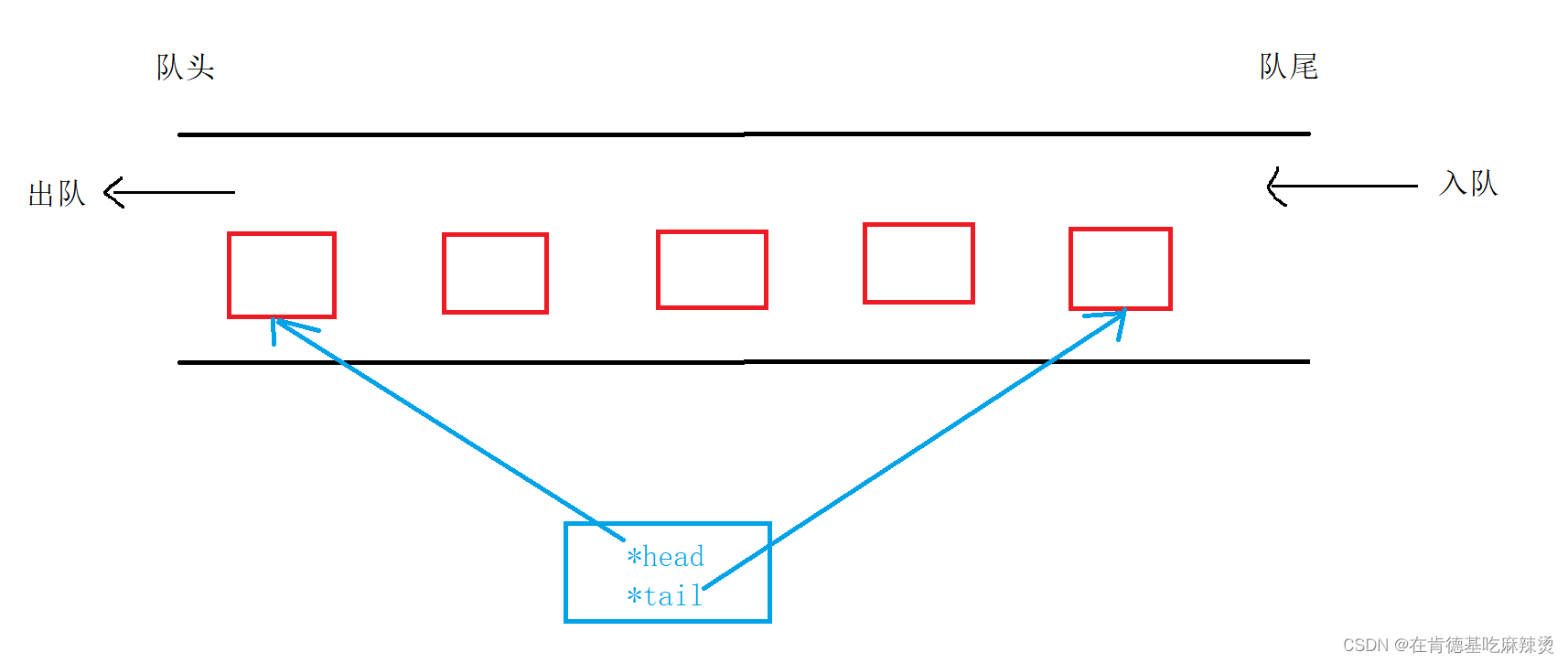
【数据结构】——队列
文章目录前言一.什么是队列,队列的特点二、队列相关操作队列的相关操作声明队列的创建1.队列的初始化2.对队列进行销毁3.判断队列是否为空队列4.入队操作5.出队操作6.取出队头数据7. 取出队尾数据8.计算队伍的人数总结前言 本文章讲述的是数据结构的特殊线性表——…...
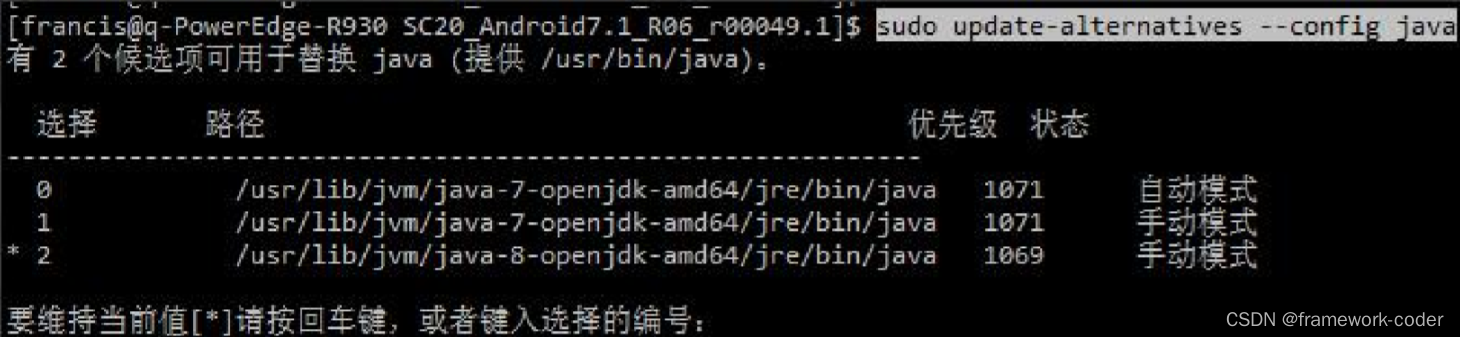
Android OTA升级常见问题的解决方法
1.1 多服务器编译 OTA 报错 Android7 以后引入了 jack-server 功能,也导致在公共服务器上 编译 Android7 以上的版本时,会出现 j ack-server 报错问题。 在多用户服务器上 编译 dist 时 会出现编译过程中 会将 port_service 和 port_admin 改为 默认的 …...
说说Hibernate
当你在实战项目中需要用到SSH时, 如果你之前只用过Mybatis那自然是不能解决问题的, 因为在很多银行类金融类项目中你可能会使用到Hibernate, 那么关于Hibernate你应该要了解什么呢, 本篇文章就以学习Hibernate框架为目的, 巩固在工作中可能需要用到的这种ORM技术, 同时也欢迎家…...

目标检测论文阅读:DETR算法笔记
标题:End-to-End Object Detection with Transformers 会议:ECCV2020 论文地址:https://link.springer.com/10.1007/978-3-030-58452-8_13 官方代码:https://github.com/facebookresearch/detr 作者单位:巴黎第九大学、…...

Golang sync.Once 源码浅析
本文分析了Golang sync.Once 源码,并由此引申,简单讨论了单例模式的实现、 atomic 包的作用和 Java volatile 的使用。 sync.Once 使用例子 sync.Once 用于保证一个函数只被调用一次。它可以用于实现单例模式。 有如下类型: type instanc…...
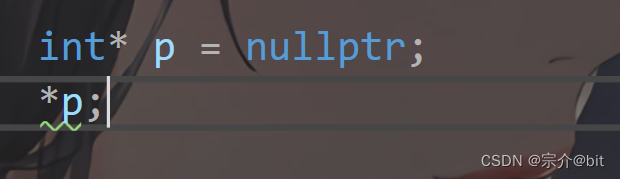
C++面向对象(上)
文章目录前言1.面向过程和面向对象初步认识2.引入类的概念1.概念与用法2.类的访问限定符及封装3.类的作用域和实例化4.类的大小计算5.this指针3.总结前言 本文将对C面向对象进行初步介绍,引入类和对象的概念。围绕类和对象介绍一些基础知识,为以后深入学…...

经常用但是不知道什么是BFC?
BFC学习 block formatting context 块级格式上下文 简单理解: 一个独立容器,内部布局不会受到外面的影响 形成条件: 1.浮动元素:float除none之外的值 2.绝对定位:position:absolute,fixed 3.display:inline-blo…...

GO的临时对象池sync.Pool
GO的临时对象池sync.Pool 文章目录GO的临时对象池sync.Pool一、临时对象池:sync.Pool1.1 临时对象的特点1.2 临时对象池的用途1.3 sync.Pool 的用法二、临时对象池中的值会被及时清理掉2.1 池清理函数2.2 池汇总列表2.3 临时对象池存储值所用的数据结构2.4 临时对象…...
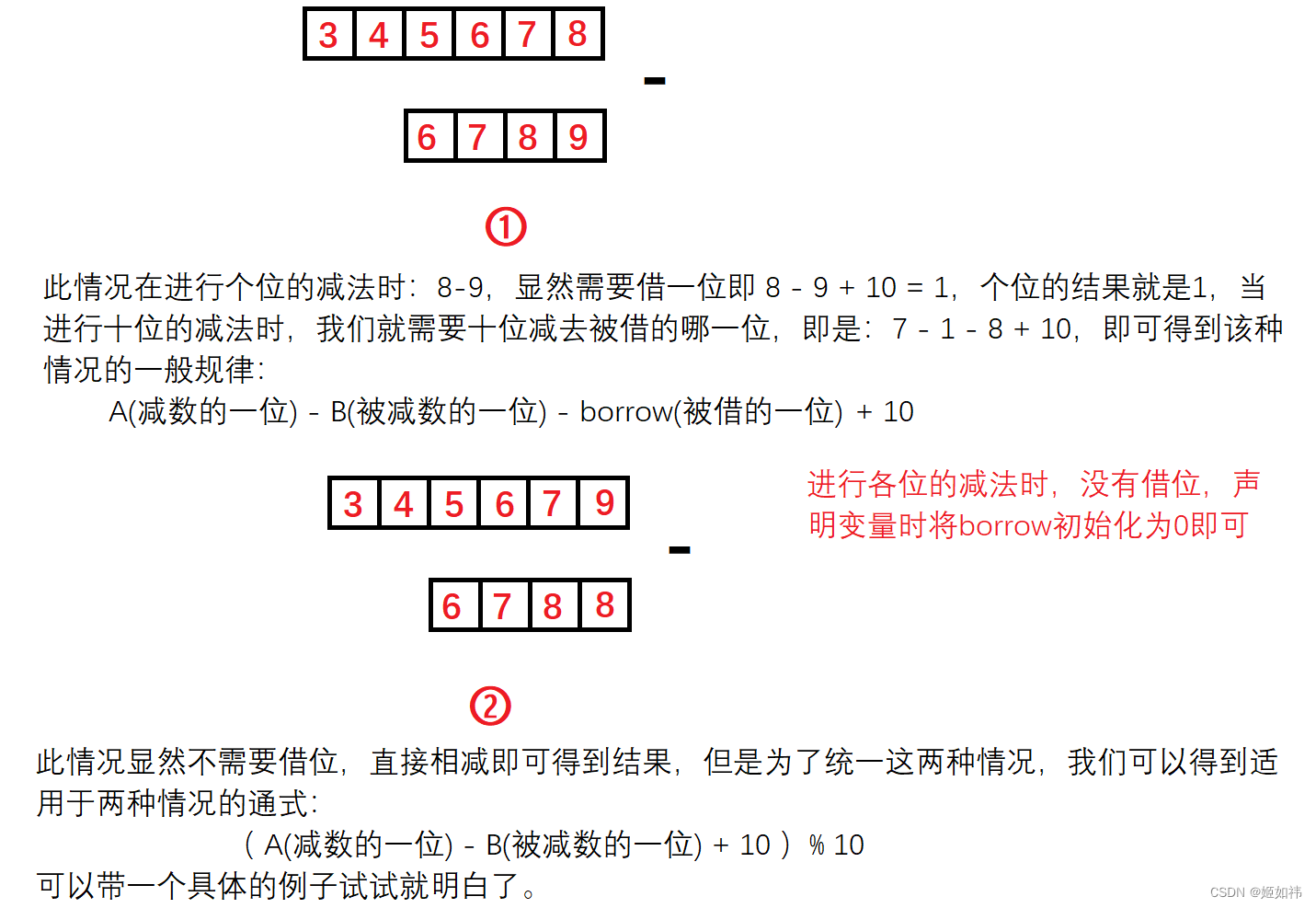
高精度算法一
目录 1. 基础知识 2. 大整数 大整数 3. 大整数 - 大整数 1. 基础知识 利用计算机进行数值计算,有时会遇到这样的问题:有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,…...

2023年全国最新食品安全管理员精选真题及答案1
百分百题库提供食品安全管理员考试试题、食品安全员考试预测题、食品安全管理员考试真题、食品安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.预包装食品的标签内容应使用规范的汉字,但可以同时使用&a…...
C++入门:引用
目录 一. 什么是引用 1.1 引用的概念 1.2 引用的定义 二. 引用的性质和用途 2.1 引用的三大主要性质 2.2 引用的主要应用 三. 引用的效率测试 3.1 传值调用和传引用调用的效率对比 3.2 值返回和引用返回的效率对比 四. 常引用 4.1 权限放大和权限缩小问题 4.2 跨…...
SpringSecurity的权限校验详解说明(附完整代码)
说明 SpringSecurity的权限校是基于SpringSecurity的安全认证的详解说明(附完整代码) (https://blog.csdn.net/qq_51076413/article/details/129102660)的讲解,如果不了解SpringSecurity是怎么认证,请先看下【SpringSecurity的安…...
Java-集合(5)
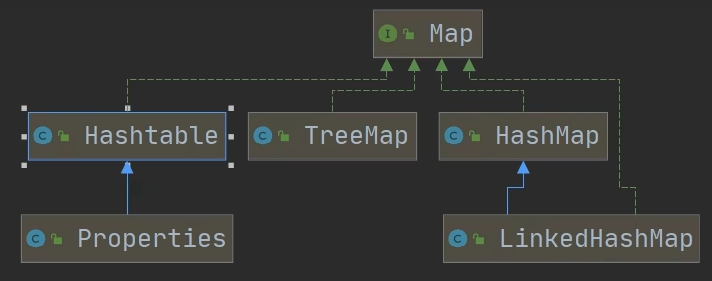
Map接口 JDK8 Map接口实现子类的特点 Map和Collection是并列关系,Map用于保存具有映射关系的数据:Key-ValueMap中的key和value可以是任何引用类型的数据,会封装到HashMap$Node对象中Map中的key不允许重复,原因和HashSet一样Map…...
设计定型阶段)
研制过程评审活动(四)设计定型阶段
1、设计定型阶段主要任务 设计定型的主要任务是对武器装备性能和使用要求进行全面考核,以确认产品是否达到《研制任务书》和《研制合同》的要求。 设计定型阶段应最终确定《产品规范》、《工艺规范》和《材料规范》的正式版本,并形成正式的全套生产图样、有关技术文件及目…...
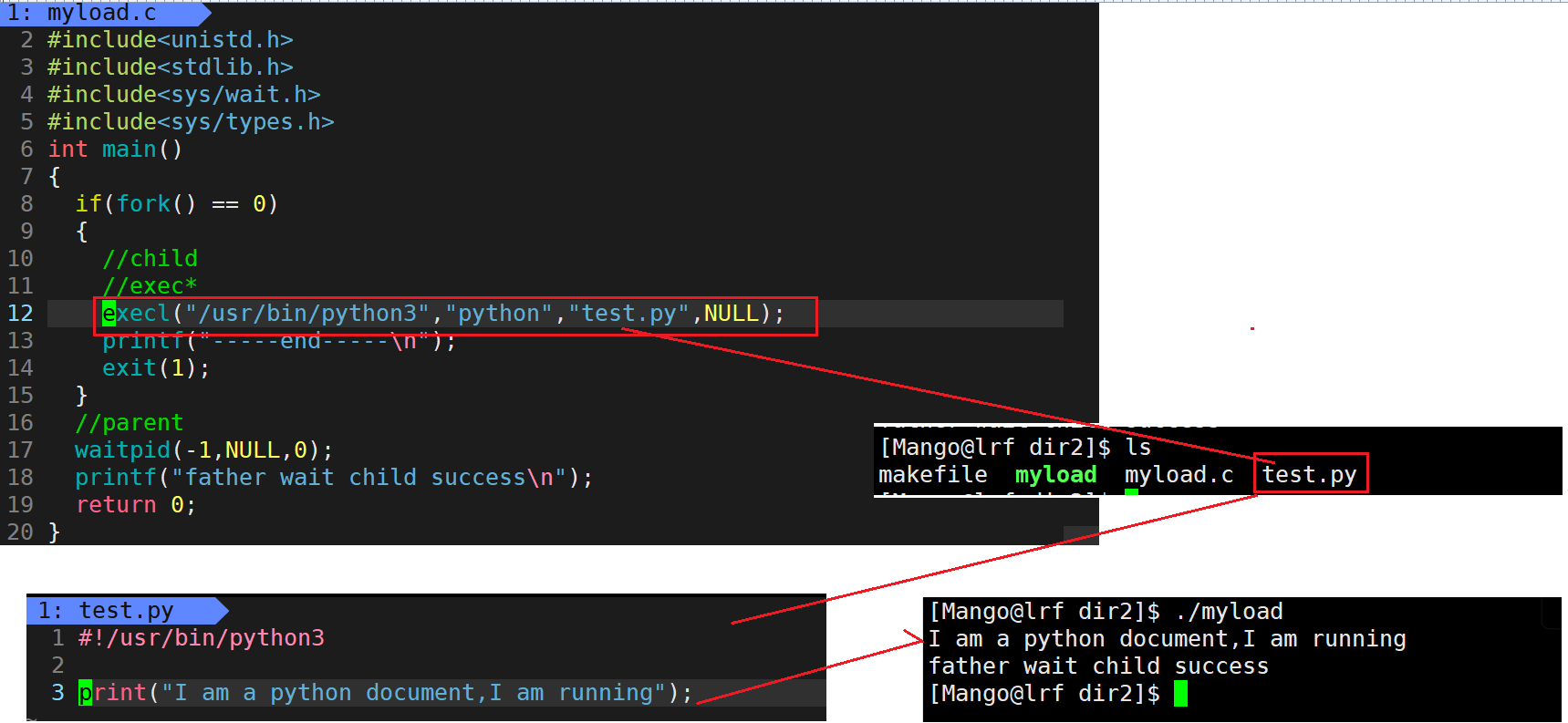
【Linux】进程替换
文章目录进程程序替换替换原理替换函数函数返回值函数命名理解在makefile文件中一次生成两个可执行文件总结:程序替换时运行其它语言程序进程程序替换 程序要运行要先加载到内存当中 , 如何做到? 加载器加载进来,然后程序替换 为什么? ->冯诺依曼 因为CPU读取数据的时候只…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
