信源分类及数学模型
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。
文章目录
- 信源分类
- 按照信源输出的信号取值分类
- 按照信源输出信号(符号间)的依赖关系
- 信源数学模型
- 离散信源
- 连续信源
- 单符号离散无记忆信源(DMS, Discrete memoryless source)
- 单个连续变量信源
- 多维离散无记忆信源
- 离散无记忆信源的扩展源
信源分类
按照信源输出的信号取值分类
1.连续(模拟)信源:
2.离散(数字)信源:

信源输出的信号是随机信号。
按照信源输出信号(符号间)的依赖关系
1、无记忆信源: 信源先后发出的符号相互统计独立,具有相同的概率分布;
2、有记忆信源: 信源先后发出的符号相互依赖。
连续信源是有记忆信源。
信源数学模型
信源:产生随机变量、随机序列和随机过程的信号源。
- 在通信系统中收信者在未收到消息以前对信源发出什么消息是不确定的,是随机的,所以可用随机变量、随机序列或随机过程来描述信源输出的消息,或者说用一个样本空间及其概率测度——概率空间来描述信源
信源的基本特性:具有随机不确定性。
香农信息论的基本观点
- 用随机变量或随机矢量来表示信源
- 用概率论和随机过程的理论来研究信息
离散信源
用离散随机变量X表示单符号离散信源(一个符号表示一完整消息,符号取值可列),X的可能取值为信源发出的各种不同符号,X的概率分布为各符号的先验概率。
例:信源 X 的取值有 NNN 个, x1,x2,…,xNx_{1}, x_{2}, \ldots, x_{N}x1,x2,…,xN , 称为信源字符集,各符号概率分布 P(x1),P(x2),…,P(xn)P\left(x_{1}\right), P\left(x_{2}\right), \ldots, P\left(x_{n}\right)P(x1),P(x2),…,P(xn) 且 ΣiP(xi)=1\Sigma_{i} P\left(x_{i}\right)=1ΣiP(xi)=1
连续信源
信源的取值为无穷不可数的连续值,其概率分布用概率密度函数p(x)表示,且
∫−∞∞p(x)dx=1\int_{-\infty}^{\infty} p(x) d x=1 ∫−∞∞p(x)dx=1
单符号离散无记忆信源(DMS, Discrete memoryless source)
如果信源 X\mathbf{X}X 的符号集 A={x1,…,xn}\mathbf{A}=\{\mathbf{x}_{1}, \ldots, \mathbf{x}_{\mathrm{n}}\}A={x1,…,xn} , 信源在离散时间发出单个符号, 且符号发生的概率相互独立, 称为单符号离散无记忆信源, 数学模型为:
[XP]=[x1⋯xnp(x1)⋯p(xn)]p(xi)≥0,∑i=1np(xi)=1\begin{array}{l} {\left[\begin{array}{l} X \\ P \end{array}\right]=\left[\begin{array}{ccc} x_{1} & \cdots & x_{n} \\ p\left(x_{1}\right) & \cdots & p\left(x_{n}\right) \end{array}\right]} \\ p\left(x_{i}\right) \geq 0, \quad \sum_{i=1}^{n} p\left(x_{i}\right)=1 \end{array} [XP]=[x1p(x1)⋯⋯xnp(xn)]p(xi)≥0,∑i=1np(xi)=1
其中 p(xi)p\left(x_{\mathrm{i}}\right)p(xi) 成为符号 xix_{\mathrm{i}}xi 的先验概率。
Example1:一个二元无记忆信源, 符号集 A={0,1} , p 为 X=0 的概率, q 为 X=1 的概率, q=1-p ; 请写出该信源的模型。
解:信源模型为[XP]=[01pq]\left[\begin{array}{l} X \\ P \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\ p & q \end{array}\right][XP]=[0p1q]
单个连续变量信源
[XP]=[x∈(a,b)p(x)],∫abp(x)dx=1\left[\begin{array}{l} X \\ P \end{array}\right]=\left[\begin{array}{c} x \in(a, b) \\ p(x) \end{array}\right], \quad \int_{a}^{b} p(x) d x=1[XP]=[x∈(a,b)p(x)],∫abp(x)dx=1,其中 p(x)≥0p(x) \geq 0p(x)≥0 为信源输出的概率密度函数
多维离散无记忆信源
若一个信源输出是一系列离散的符号, 而每个符号又是随机的, 即信源输出为一系列随机变量 (随机矢量), 从而信源的输出可用 L 维随机矢量 [X1,X2,…,XL]\left[X_{1}, X_{2}, \ldots, X_{L}\right][X1,X2,…,XL] 来描述, 其中 L\boldsymbol{L}L 为有限正整数或可数 的无限值。
上述随机矢量中, 若每个随机变量 Xi(i=1,2,…,L)X_{i}(\boldsymbol{i}=1,2, \ldots, L)Xi(i=1,2,…,L) 都是离散的, 则可用 L 维离散概率空间来描述这类信源。
即若 L\boldsymbol{L}L 维随机矢量 X=[X1X2…XL],XiX=\left[X_{1} X_{2} \ldots X_{L}\right], X_{\mathrm{i}}X=[X1X2…XL],Xi 的具体取值为 x∈(a1,a2,…an,)x \in\left(a_{1}, a_{2}, \ldots a_{n},\right)x∈(a1,a2,…an,) , 对应概率为 PX(x)=P(x1x2…xL)P_{X}(x)=P\left(x_{1} x_{2} \ldots x_{L}\right)PX(x)=P(x1x2…xL) 为 L\boldsymbol{L}L 维联合概率分布, 则该信源的数学模型为
(XLP(x))=((a1a1…a1)…(a1a2…am)…(anan…an)P(a1a1…a1)…P(a1a2…am)…P(anan…an))\begin{array}{l} \left(\begin{array}{c} X^{L} \\ P(x) \end{array}\right) =\left(\begin{array}{ccccc} \left(a_{1} a_{1} \ldots a_{1}\right) & \ldots & \left(a_{1} a_{2 \ldots} a_{m}\right) & \ldots & \left(a_{n} a_{n} \ldots a_{n}\right) \\ P\left(a_{1} a_{1} \ldots a_{1}\right) & \ldots & P\left(a_{1} a_{2 \ldots} a_{m}\right) & \ldots & P\left(a_{n} a_{n} \ldots a_{n}\right) \end{array}\right) \end{array} (XLP(x))=((a1a1…a1)P(a1a1…a1)……(a1a2…am)P(a1a2…am)……(anan…an)P(anan…an))
其中离散消息序列长度为 L\boldsymbol{L}L , 序列每符号有 n\boldsymbol{n}n 种取值, 整个消息序列共有 nLn^{L}nL 种取值。
当输出序列中的前后消息(符号)相互统计独立, 且具有相同的概率分布, 则 L 维随机矢量的联合概率分布满足
P(X)=∏i=1LP(Xi=xj),j=1,2,…,nP(X)=\prod_{i=1}^{L} P\left(X_{i}=x_{\boldsymbol{j}}\right), \boldsymbol{j}=1,2, \ldots, n P(X)=i=1∏LP(Xi=xj),j=1,2,…,n
即 L\boldsymbol{L}L 维随机矢量的联合概率分布可用随机矢量中单个随机变量的概率乘积来表示。这种信源为离散无记忆信源。
离散无记忆信源的扩展源
设信源为 X\mathrm{X}X , 则由 X\mathrm{X}X 构成 N 维随机矢量集合 XN=[X1X2…XN],(\mathbf{X}^{N}=\left[X_{1} X_{2} \ldots X_{N}\right], \quad\left(\right.XN=[X1X2…XN],( 其中 Xi\mathbf{X}_{\mathbf{i}}Xi 与 X\mathbf{X}X 同分布, 取自同一信源 X ),称为信源 X\mathrm{X}X 的 N 次扩展源。
Example2:求例1中信源的二次扩展源模型:
Ex1\mathbf{E x} 1Ex1 的二元无记忆信源模型为[XP]=[01pq]\left[\begin{array}{l} X \\ P \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\ p & q \end{array}\right][XP]=[0p1q]
其二次扩展信源为
[X2p(α)]=[α1(00)α2(01)α3(10)α4(11)p(α1)p(α2)p(α3)p(α4)]p(α1)=p2,p(α2)=p(1−p)=p(α3)p(α4)=(1−p)2\left[\begin{array}{l}X^{2} \\ p(\alpha)\end{array}\right]=\left[\begin{array}{llll}\alpha_{1}(00) & \alpha_{2}(01) & \alpha_{3}(10) & \alpha_{4}(11) \\ p\left(\alpha_{1}\right) & p\left(\alpha_{2}\right) & p\left(\alpha_{3}\right) & p\left(\alpha_{4}\right)\end{array}\right] \\ p\left(\alpha_{1}\right)=p^{2}, p\left(\alpha_{2}\right)=p(1-p)=p\left(\alpha_{3}\right) p\left(\alpha_{4}\right)=(1-p)^{2}[X2p(α)]=[α1(00)p(α1)α2(01)p(α2)α3(10)p(α3)α4(11)p(α4)]p(α1)=p2,p(α2)=p(1−p)=p(α3)p(α4)=(1−p)2
一个离散无记忆信源的 N\mathbf{N}N 次扩展信源描述如下:
设 X\mathbf{X}X 为离散无记忆信源, 则 X\mathbf{X}X 的 N\mathbf{N}N 次扩展信源记为XN,XN=[X1X2…XN]\mathbf{X}^{N} , \mathbf{X}^{N}=\left[X_{1} X_{2} \ldots X_{N}\right]XN,XN=[X1X2…XN] , 其模型为
(XNP)=(a1⋯aMp(a1)⋯p(aM))\left(\begin{array}{c} \mathbf{X}^{N} \\ P \end{array}\right)=\left(\begin{array}{ccc} a_{1} & \cdots & a_{M} \\ p\left(a_{1}\right) & \cdots & p\left(a_{M}\right) \end{array}\right) (XNP)=(a1p(a1)⋯⋯aMp(aM))
每个 XiX_{i}Xi 取自同一个字母表 A={a1,a2,…,aN}A=\{a_{1}, a_{2}, \ldots, a_{N}\}A={a1,a2,…,aN} , 且 XiX_{i}Xi 与 X\mathbf{X}X 同分布,因此, XN\mathbf{X}^{\mathrm{N}}XN 的符号集为 AN={a1,…,aN},ajA^{N}=\{\boldsymbol{a}_{1}, \ldots, \boldsymbol{a}^{N}\}, \boldsymbol{a}_{j}AN={a1,…,aN},aj 为多维信源中的一个矢量, 即 aj∈ANa_{j} \in A^{N}aj∈AN , 矢量的个数为nNn^{N}nN,aj=(aj1aj2,…,,ajN)\boldsymbol{a}_{\boldsymbol{j}}=\left(a_{j_{1}} a_{j_{2}, \ldots,}, a_{j N}\right)aj=(aj1aj2,…,,ajN),ajka_{j k}ajk 为 $\boldsymbol{a}_{j} $的第 k\mathbf{k}k 个分量, 且 p(aj)=∏k=1Npjkp\left(\boldsymbol{a}_{j}\right)=\prod_{k=1}^{N} p_{j k}p(aj)=∏k=1Npjk ,pjkp_{j k}pjk 为第 j\mathrm{j}j 个矢量第 k\mathrm{k}k 个分量取符号 ajk\boldsymbol{a}_{\mathrm{jk}}ajk 的概率。
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.
相关文章:

信源分类及数学模型
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录信源分类按照信源…...
Games101-202作业1
一. 将模型从模型空间变换到世界空间下 在这个作业下,我们主要进行旋转的变换。 二.视图变换 ,将相机移动到坐标原点,同时保证物体和相机进行同样的变换(这样对形成的图像没有影响) 在这个作业下我们主要进行摄像机的平移变换&am…...
Linux系统之终端管理命令的基本使用
Linux系统之终端管理命令的基本使用一、检查本地系统环境1.检查系统版本2.检查系统内核版本二、终端介绍1.终端简介2.Linux终端简介3.终端的发展三、终端的相关术语1.终端模拟器2.tty终端3.pts终端4.pty终端5.控制台终端四、终端管理命令ps1.直接使用ps命令2.列出登录详细信息五…...

【Mongoose笔记】MQTT 服务器
【Mongoose笔记】MQTT 服务器 简介 Mongoose 笔记系列用于记录学习 Mongoose 的一些内容。 Mongoose 是一个 C/C 的网络库。它为 TCP、UDP、HTTP、WebSocket、MQTT 实现了事件驱动的、非阻塞的 API。 项目地址: https://github.com/cesanta/mongoose学习 下面…...

数据结构概述
逻辑结构 顺序存储 随机访问是可以通过下标取到任意一个元素,即数组的起始位置下标 链式存储 链式存储是不连续的,比如A只保留了当前的指针,那么怎么访问到B和C呢 每个元素不仅存储自己的值还使用额外的空间存储指针指向下一个元素的地址&a…...
【前端】Vue3+Vant4项目:旅游App-项目总结与预览(已开源)
文章目录项目预览首页Home日历:日期选择开始搜索位置选择上搜索框热门精选-房屋详情1热门精选-房屋详情2其他页面项目笔记项目代码项目数据项目预览 启动项目: npm run dev在浏览器中F12: 首页Home 热门精选滑动到底部后会自动加载新数据&a…...
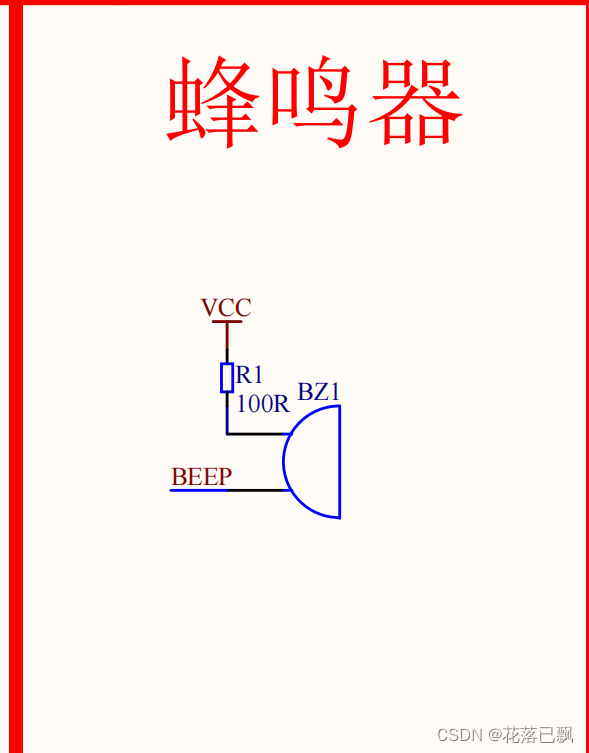
51单片机蜂鸣器的使用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、有源蜂鸣器和无源蜂鸣器的区别二、代码编写总结前言 本文旨在介绍如何使用51单片机驱动蜂鸣器。 一、有源蜂鸣器和无源蜂鸣器的区别 有源蜂鸣器是一种电子…...

算法练习-链表(二)
算法练习-链表(二) 文章目录算法练习-链表(二)1. 奇偶链表1.1 题目1.2 题解2. K 个一组翻转链表2.1 题目2.2 题解3. 剑指 Offer 22. 链表中倒数第k个节点3.1 题目3.2 题解3.2.1 解法13.2.2 解法24. 删除链表的倒数第 N 个结点4.1 …...
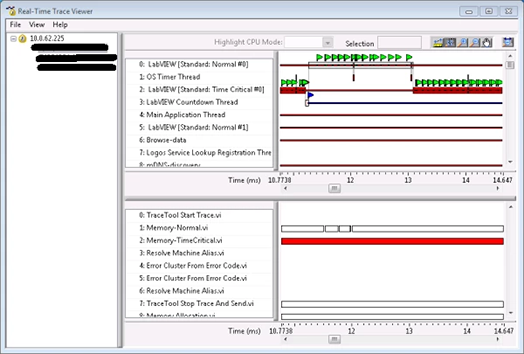
LabVIEW使用实时跟踪查看器调试多核应用程序
LabVIEW使用实时跟踪查看器调试多核应用程序随着多核CPU的推出,开发人员现在可以在LabVIEW的帮助下充分利用这项新技术的功能。并行编程在为多核CPU开发应用程序时提出了新的挑战,例如同步多个线程对共享内存的并发访问以及处理器关联。LabVIEW可自动处理…...

【go语言grpc之client端源码分析二】
go语言grpc之server端源码分析二DialContextparseTargetAndFindResolvergetResolvernewCCResolverWrapperccResolverWrapper.UpdateStatecc.maybeApplyDefaultServiceConfigccBalancerWrapper.updateClientConnState上一篇文章分析了ClientConn的主要结构体成员,然后…...

centos7安装RabbitMQ
1、查看本机基本信息 查看Linux发行版本 uname -a # Linux VM-0-8-centos 3.10.0-1160.11.1.el7.x86_64 #1 SMP Fri Dec 18 16:34:56 UTC 2020 x86_64 x86_64 x86_64 GNU/Linux cat /etc/redhat-release # CentOS Linux release 7.9.2009 (Core)2、创建创建工作目录 mkdir /…...
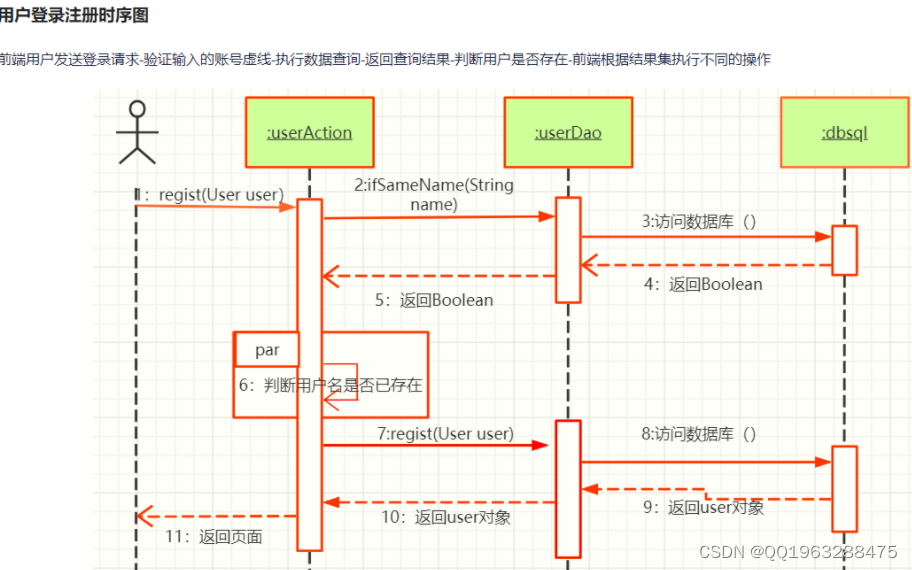
node基于springboot 口腔卫生防护口腔牙科诊所管理系统
目录 1 绪论 1 1.1课题背景 1 1.2课题研究现状 1 1.3初步设计方法与实施方案 2 1.4本文研究内容 2 2 系统开发环境 4 2.1 JAVA简介 4 2.2MyEclipse环境配置 4 2.3 B/S结构简介 4 2.4MySQL数据库 5 2.5 SPRINGBOOT框架 5 3 系统分析 6 3.1系统可行性分析 6 3.1.1经济可行性 6 3.…...
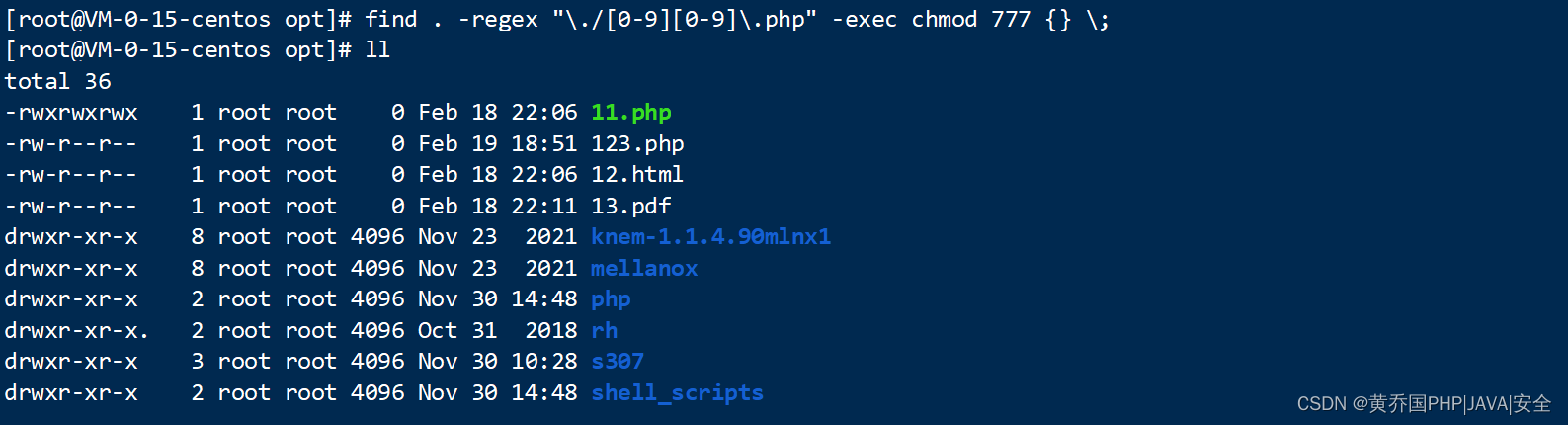
Linux常用命令之find命令详解
简介 find命令主要用于:用来在指定目录下查找文件。任何位于参数之前的字符串都将被视为欲查找的目录名。 如果使用该命令时,不设置任何参数,则find命令将在当前目录下查找子目录与文件。并且将查找到的子目录和文件全部进行显示。 是我们在…...

CMake 入门学习4 软件包管理
CMake 入门学习4 软件包管理一、Linux下的软件包管理1. 检索已安装的软件包2. 让自己编译软件支持pkg-config搜索3. 在CMakeLists查找已安装的软件包二、适合Windows下的包管理工具1. vcpkg2. Conan(1) 安装Conan(2) 配置Conan(3) 创建工程(4) 安装依赖库(5) 使用依赖库三、CMa…...

【数据库数据乱码错误】存进去的数据乱码(???)
目录 1.当我新增一条数据的时候,成功后查看数据库中的数据时,竟然变成???乱码格式了: 2.那么问题有3处需要注意: 第一:settings配置 第二:POM文件 第三:…...
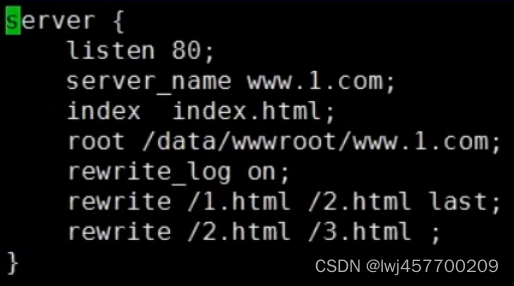
rewrite中的if、break、last
目录 rewrite 作用: 依赖: 打开重定向日志: if 判断: location {} 本身有反复匹配执行特征 在 location 中加入 break 和 last (不一样) 加了break后,立刻停止向下 且 跳出。 加了last…...

JavaSE-线程池(5)- 建议使用的方式
JavaSE-线程池(5)- 建议使用的方式 虽然JDK Executors 工具类提供了默认的创建线程池的方法,但一般建议自定义线程池参数,下面是阿里巴巴开发手册给出的理由: 另外Spring也提供了线程池的实现,比如 Thread…...

城市轨道交通供电系统研究(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

什么是 RESTful 风格?
一、什么是 REST ? REST即表述性状态传递(英文:Representational State Transfer,简称REST)是Roy Thomas Fielding博士在2000年他的博士论文中提出来的一种软件架构风格。它是一种针对网络应用的设计和开发方式&#…...
从业6年,对敏捷和自动化测试的一点心得
不久前,参加Thoughtworks组织的一场自动化测试的分享,同事由于出差国外不能参加,特意嘱托我提问两个问题: 在互联网这个将“敏捷”与“持续集成”进行积极实践的环境里,“敏捷测试”与“自动化测试”成了一个大家经常…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
