11-数据结构-栈和队列的应用(C语言)
栈和队列的应用
目录
栈和队列的应用
一、括号匹配(栈)
二、表达式的各种转换
(1)中缀转后缀(手工)
(2)后缀转中缀表达式(手工)
(3)中缀转后缀(栈)
(4)中缀转后缀(树)
(5)后缀表达式求值
(6)中缀表达式求值(栈)
三、栈在递归的应用
四、队列的应用
一、括号匹配(栈)
思想:括号匹配就是有() [] {},各种各样的括号,符合相应匹配的括号正确,否则为非法情况。
主要利用栈,给括号凑存入数组中。然后读取,当读取左括号时,入栈,当遇到右括号时,栈内出栈,与之对比,若匹配则继续扫描数组,否则则非法,程序结束,非法情况除了括号不对应外,还有,两种,一个是扫到右括号,去栈内拿括号,结果栈空了。另一种则是栈内还有括号,但是数组已经读取完了。
代码如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
//创建栈
typedef struct
{char data[50];int top;
}SqStack;
void InitStack(SqStack *s)
{s->top=-1;
}
//入栈
void StackPush(SqStack *s,char x)
{s->top++;s->data[s->top]=x;
}
//出栈
void StackPop(SqStack *s,char *e)
{if(s->top == -1){printf("栈都空了,没东西了\n");exit(-1);}*e =s->data[s->top];s->top--;
}
void KuohaoMatch(char *num,int len)
{SqStack s;InitStack(&s);int i;for(i=0;i<len;i++){if(num[i]=='(' || num[i]=='[' || num[i]== '{') StackPush(&s,num[i]);else{if(s.top== -1){printf("栈内没有匹配的括号,匹配失败\n"); exit(-1);}char e='a';StackPop(&s,&e);if(num[i]=='}' && e != '{') {printf("}匹配失败\n");exit(-1);}if(num[i]==']' && e != '[') {printf("]匹配失败\n");exit(-1);}if(num[i]==')' && e != '(') {printf(")匹配失败\n");exit(-1);}}} if(s.top==-1)printf("匹配完毕,未发现异常,匹配成功\n");elseprintf("栈内仍有括号,匹配失败\n"); }int main()
{char num[10]="{([])}";int len=strlen(num);KuohaoMatch(num,len);return 0;
}二、表达式的各种转换
表达式,根据操作符的位置,有不同的叫法,如a+b,为中缀,因为+在中间。同理+ab为前缀,ab-为后缀。
我们日常见到的为中缀表达式,但如果让计算机识别的话,比较费劲,因此我们如果给中缀表达式转化为后缀表达式(当计算机遇到两个操作数和一个操作算符就会直接计算)或前缀表达式(当计算机遇到一个操作算符和两个操作数就会直接计算),这计算机就可直接进行计算,
(1)中缀转后缀(手工)
如:A+B*(C-D)-E/F.
由于同级操作算符,中缀可以转不同的后缀表达式,不唯一,
两种计算方法:
方法一:我们可以根据优先级,一块一块的去算,先计算(C-D)为CD-,E/F为EF/,而B*(CD-)也是两操作数,因此为BCD-*,随后A+(BCD-*)为两个操作数,所以ABCD-*+,最后(ABCD-*+)-(EF/)为两个操作数,因此为:ABCD-*+EF/-.

方法二:从左至右书写字符,按照优先级,如果能计算,优先计算,

(2)后缀转中缀表达式(手工)
后缀表达式则跟中缀思想差不多,也是块思想,每一个小的操作计算,都是一小块一个整体,又内向外,逐层计算。
注意:变为中缀,要根据优先级,加括号记得,此外由后缀转中缀,结果唯一。
(3)中缀转后缀(栈)
之前是手工草稿推的,一般选择填空应用,够用了,不过如果,要求按照栈的思想,去实现中缀转后缀,则需要学一下这个。
大致思想:遍历到字符,直接输出,遍历到操作符,给它入栈,如果又遇到操作符,便与栈顶的操作符对比,如果栈顶的操作符优先级高,则给栈顶弹出,优先级低的,入栈。此外遇到(),先入(,之后遇见),则给栈内(之前的内容都弹出。

(4)中缀转后缀(树)
即给表达式,写成树的形式,其中根节点为符号,每一棵树为一个小计算整体,此外选每颗树的根时,先理清楚计算先后,以及整体。
给中缀先转化成树的形式。
根据计算优先级,划分括号,然后再原意义一样的情况下,组成树。最开始的根节点为操作符。
如:A+B*(C-D)-E/F

给出表达式树,求中缀或前缀,后缀表达式:

给每个结点表上1 2 3,然后从最上层开始画线,跑一圈,其中1代表前缀,2中缀,3后缀
(5)后缀表达式求值
利用栈的大致思想:给操作数入栈,遇到操作符,从栈中弹出两个数,进行计算,计算结果,接着入栈。依次类推。
最后几步,类似这样,一直弄完,

手工求解。
方法一:可先给后缀表达为中缀,(画框法,没每一个小块先转换,由内向外逐层转换)
方法二:遇到两个操作数和一个操作符,三者挨着的,优先计算,依次类推。前缀一样思想
(6)中缀表达式求值(栈)
创建两个栈,一个栈存操作符,一个栈存操作数,
当识别到操作符,并且比操作符栈顶操作符优先级小时,弹出两个数,进行计算,并入字符数栈。
优先级相同时,遵循最左原则,操作符栈内的优先计算,
如:3*(7-2),另外,进行栈求的时候,需要给表达式两边加上#号。
#3*(7-2)#
操作符栈:# * ( -
操作数栈:3 7 2
栈内-比)优先级高,-弹出,7 2 弹出,计算,7-2=5,5入数栈,另外计算减法时,按照原本意义计算,不能减反了
操作符栈:# *
操作数栈:3 5
栈内*比栈外,#优先级高,*弹出,3 5 弹出,计算3*5=15,15入栈
操作符栈:##
操作数栈:15
#检测到与它相等的#,程序结束。
三、栈在递归的应用
这里即递归的意义。
递归就是在系统栈中,开辟临时空间,进行操作。逐层创建内推,到最内层的结束条件时,再往回返回。
四、队列的应用
二叉树层次遍历,
从上而下,从左至右,一个树一个树的进行,每次遍历都是入队,然后从对头挨个处理即可!
相关文章:

11-数据结构-栈和队列的应用(C语言)
栈和队列的应用 目录 栈和队列的应用 一、括号匹配(栈) 二、表达式的各种转换 (1)中缀转后缀(手工) (2)后缀转中缀表达式(手工) (3)中缀转后缀(栈) (4)中缀转后缀(树) (5)后缀表达式求值 (6)中缀表达式求值(栈…...
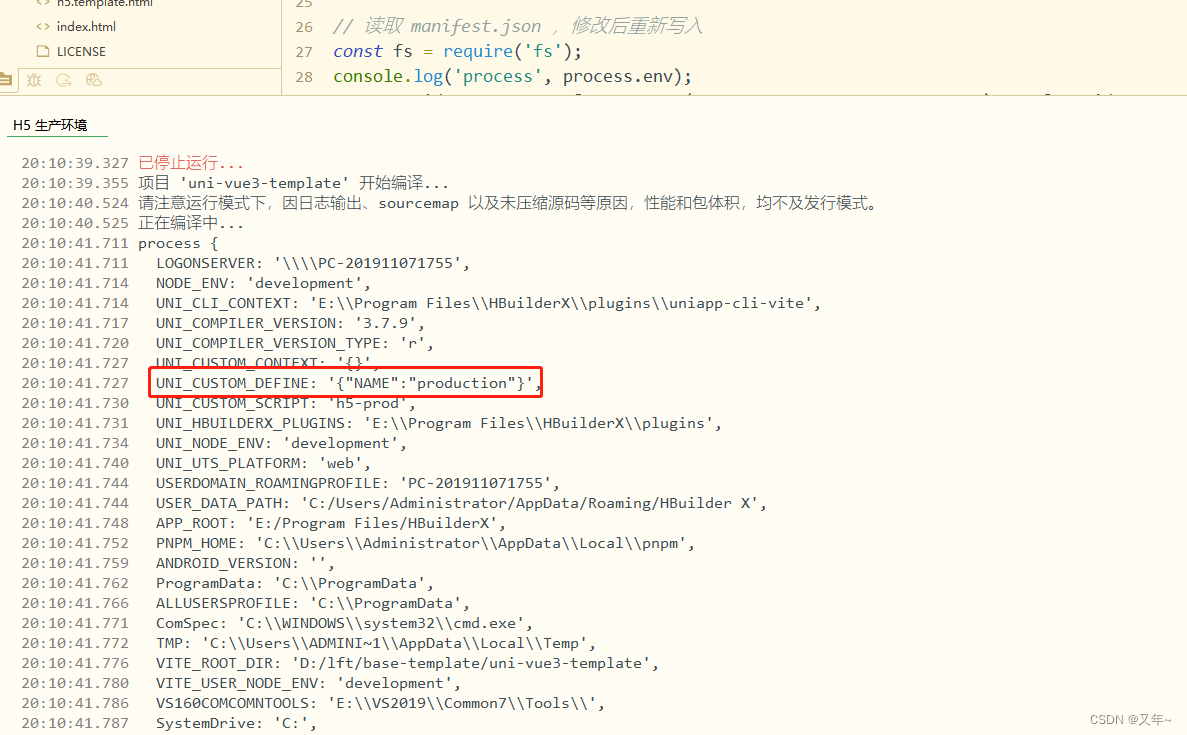
uni-app自定义多环境配置,动态修改appid
背景 在企业级项目开发中,一般都会分为开发、测试、预发布、生产等多个环境,在工程化中使用不同的打包命令改变环境变量解决不同环境各种变量需要手动修改的问题,比如接口请求地址,不同环境的请求路径前缀都是不同的。在使用uni-…...
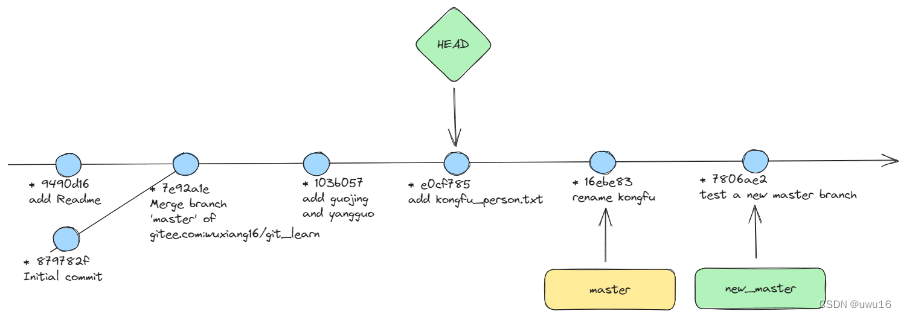
04 - 分离头指针情况、理解HEAD和branch
查看所有文章链接:(更新中)GIT常用场景- 目录 文章目录 1. 分离头指针2. HEAD和branch2.1 branch的一些操作2.2 HEAD 1. 分离头指针 分离头指针detached HEAD是一种HEAD指针指向了某一个具体的 commit id,而不是分支的情况。 切换…...
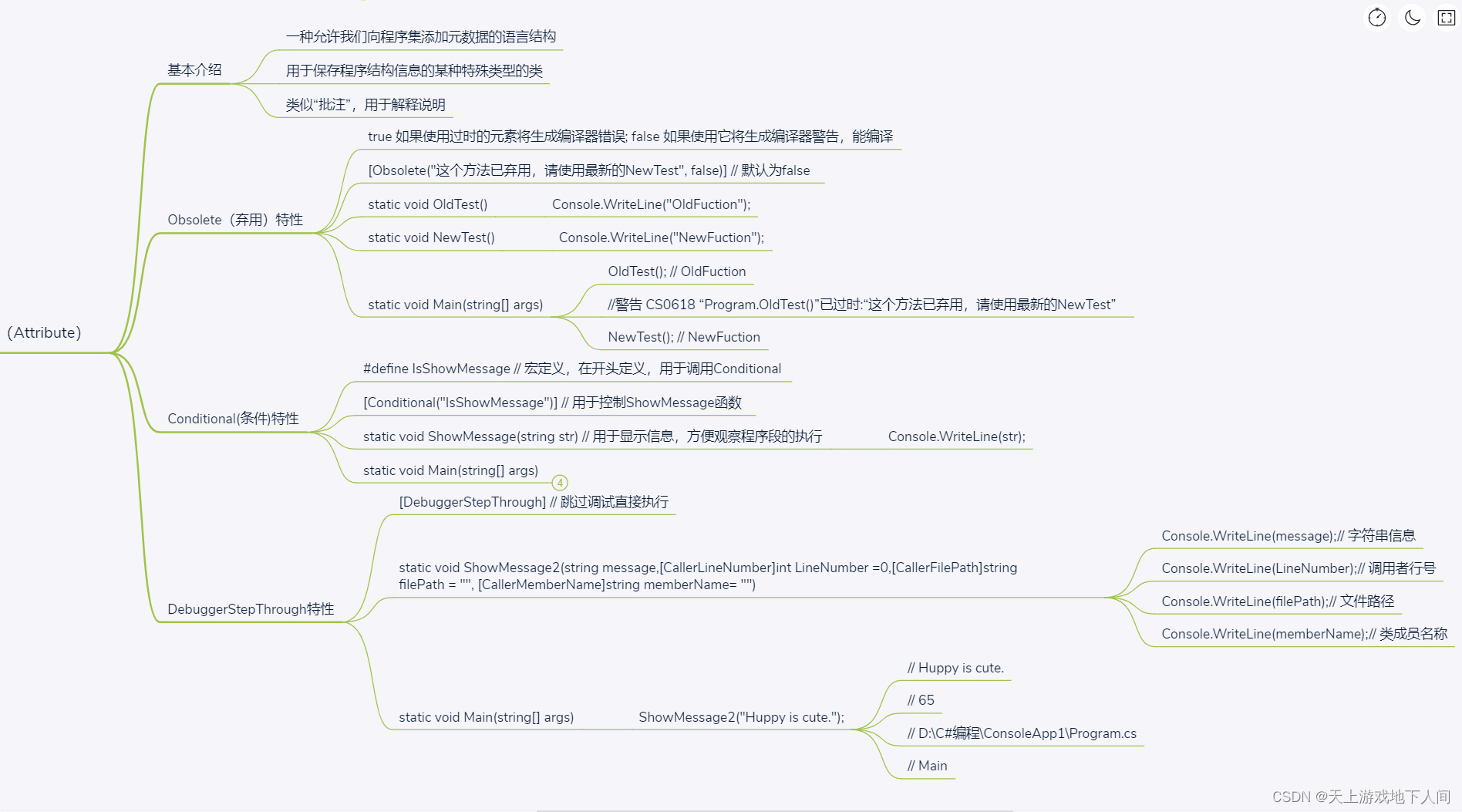
C#__基本特性和使用
// 特性(attribute): // 一种允许我们向程序集添加元数据的语言结构 // 用于保存程序结构信息的某种特殊类型的类 // 类似“批注”,用于解释说明 #define IsShowMessage // 宏定义,在开头定义࿰…...
)
mysql(3)
分库分表 分库:将数据库中的数据分散到不同数据库上,可以垂直分库和水平分库。 1.垂直分库:把单一的数据按照业务进行划分,不同的业务使用不同的数据库,进而将一个数据库的压力分散到多个数据库。 2.水平分库&#…...

阿里巴巴常用的12个后端开发工具
1 阿尔萨斯Java在线诊断工具 Arthas是一款用于Java应用程序的在线诊断工具,由阿里巴巴于2018年9月开源。 典型场景: 您不知道从中加载类的特定JAR包。 您想弄清楚为什么您的系统会抛出各种与类相关的异常。 您不知道为什么修改后的代码无法执行。您不…...

php base64转图片保存本地
调用函数 public function base64(){$img $this->request->param(img);$img data:image/jpeg;base64,/9j/4AAQSkZJRgABAQEAkACQAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIy…...
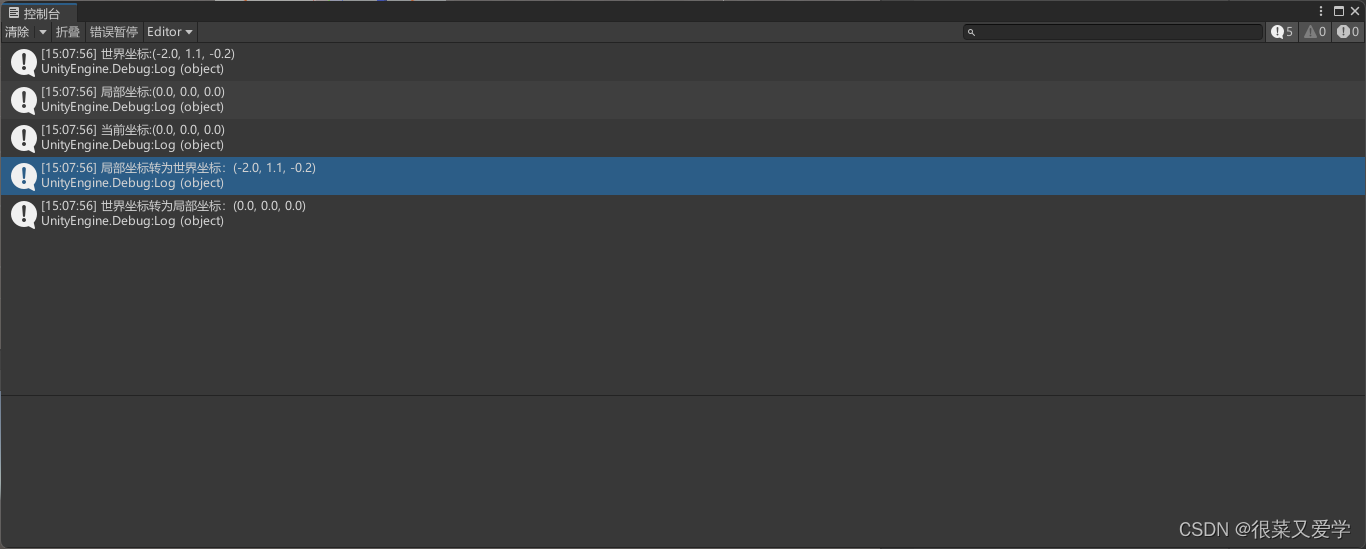
unity物体移动至指定位置
物体坐标与物体移动 世界坐标与局部坐标之间的转换物体移动至指定位置需求思路注意 世界坐标与局部坐标之间的转换 在Unity中,物体的坐标分为局部坐标和世界坐标。 局部坐标是相对于物体的父对象的坐标系,而世界坐标是相对于场景的整体坐标系。 使用tr…...

详解C#-static void Main(string[] args)
目录 简介: 举例: 输出结果:编辑 总结: 简介: 在C#中static void Main(string[] args)这个句话有什么作用,分别代表什么意思!! 这句话是入口函数的声明,指定了C#程序的入口点,并定义了一个名为”Mai…...

中大许少辉博士《乡村振兴战略下传统村落文化旅游设计》中国建筑工业出版社八一付梓。
中大许少辉博士《乡村振兴战略下传统村落文化旅游设计》中国建筑工业出版社八一付梓。...
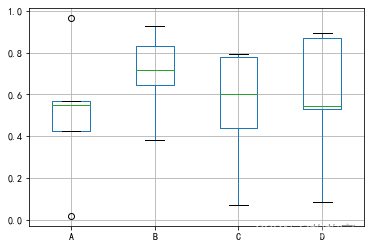
Matplotlib数据可视化(五)
目录 1.绘制折线图 2.绘制散点图 3.绘制直方图 4.绘制饼图 5.绘制箱线图 1.绘制折线图 import matplotlib.pyplot as plt import numpy as np %matplotlib inline x np.arange(9) y np.sin(x) z np.cos(x) # marker数据点样式,linewidth线宽,li…...

Python爬虫——requests_post请求
import requests import jsonurl https://fanyi.baidu.com/sugheaders {User-Agent: ,Cookie: }data {kw: hello }response requests.post(url, data, headersheaders)content response.textobj json.loads(content.encode(utf-8)) print(obj)总结: post请求…...
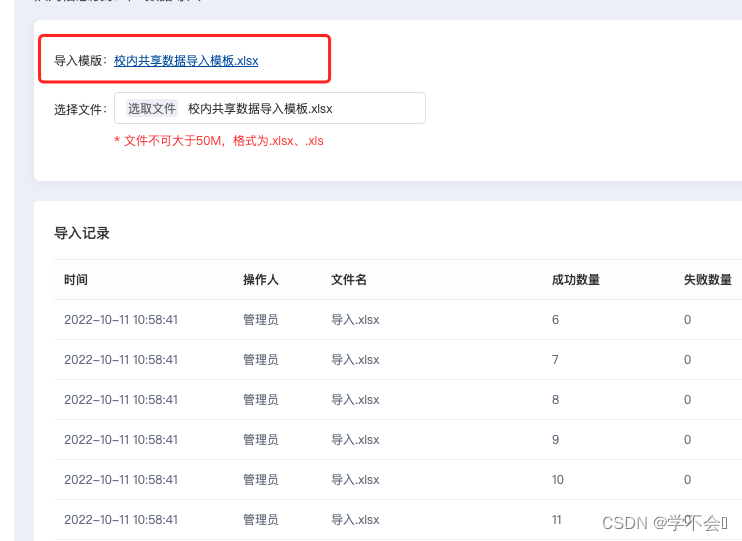
excel 下载方法封装
1.首先需要拿到后端返回的URL下载地址 2.写个下载方法 // url 接口返回的下载地址。例如:https://cancer-research.oss-cn-beijing.aliyuncs.com/yuance-platform-permission/校内共享数据导入模板.xlsx // name 文件名称 例如: 校内共享数据导入模板 /…...

按日,周,月,季,年统计;获取对应的时间段
按日,周,月,季,年统计;获取对应的时间段 1.周实体类:WeekEntity.java package com.test.common.entity;import java.time.LocalDate;public class WeekEntity {private String day;/*** 开始日期**/privat…...
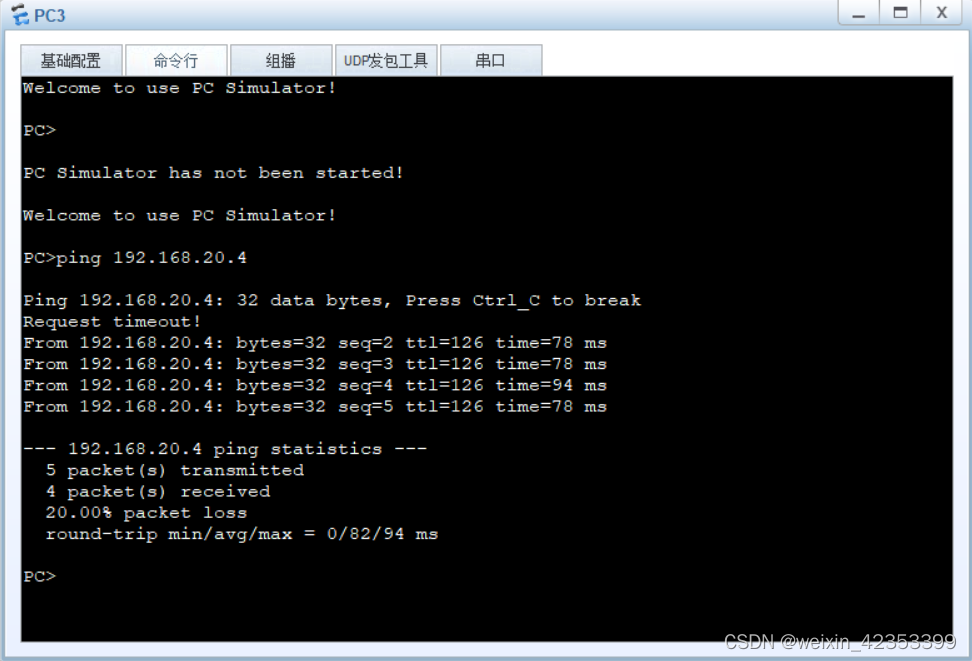
【eNSP】交换机(vlan和vlan间通信)
【eNSP】交换机(vlan和vlan间通信) 原理术语过程 实验根据图片连接模块配置设备名称和IP地址配置交换机交换机链路指定sw1配置sw2配置 设置网关交换机互联实验设置查看设置结果 ospf配置 原理 HUB集线器:它的作用可以简单的理解为将一些机器…...
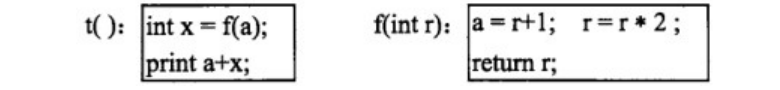
2011年下半年 软件设计师 上午试卷2
博主介绍:✌全网粉丝3W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...

Linux中安装MySQL8版本,安装MySQL步骤,MySQL8离线安装
Linux中安装MySQL8版本的步骤如下: 1.检查下libaio.so.1的位置 [roottdx ]# whereis libaio.so.1 libaio.so: /usr/lib64/libaio.so.1 如果没有找到该文件 (1).在线安装 [roottdx ]# yum install -y libaio (2).离线安装: 上传之后执行命令安装&#…...

MES生产管理系统如何与ERP系统集成
MES生产管理系统和ERP企业管理系统是制造企业信息化的重要组成部分,它们在生产管理、资源计划和业务流程等方面发挥着重要作用。实现MES与ERP系统的集成,可以更好地优化企业生产流程,提高生产效率和降低成本。本文将探讨MES管理系统解决方案如…...

Kafka如何保证消息⼀定能被消费
Kafka 通过多种机制来保证消息一定能被消费,从而实现数据的可靠性和持久性。 以下是一些常见的方法和策略来提高消息的可靠性: 复制机制: Kafka 使用了分区和副本的概念。每个分区可以有多个副本,分布在不同的 Broker 上。当消息…...

[USACO1.5] 八皇后 Checker Challenge
题目描述 一个如下的 6 x 6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。 上面的布局可以用序列 2 4 6 1 3 5 来描述,第…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

GC1808:高性能音频ADC的卓越之选
在音频处理领域,高质量的音频模数转换器(ADC)是实现精准音频数字化的关键。GC1808,一款96kHz、24bit立体声音频ADC,以其卓越的性能和高性价比脱颖而出,成为众多音频设备制造商的理想选择。 GC1808集成了64倍…...

MAZANOKE结合内网穿透技术实现跨地域图像优化服务的远程访问过程
文章目录 前言1. 关于MAZANOKE2. Docker部署3. 简单使用MAZANOKE4. 安装cpolar内网穿透5. 配置公网地址6. 配置固定公网地址总结 前言 在数字世界高速发展的今天,您是否察觉到那些静默增长的视觉数据正在悄然蚕食存储空间?随着影像记录成为日常习惯&…...

论文笔记:Large Language Models for Next Point-of-Interest Recommendation
SIGIR 2024 1 intro 传统的基于数值的POI推荐方法在处理上下文信息时存在两个主要限制 需要将异构的LBSN数据转换为数字,这可能导致上下文信息的固有含义丢失仅依赖于统计和人为设计来理解上下文信息,缺乏对上下文信息提供的语义概念的理解 ——>使用…...

【RabbitMQ】- Channel和Delivery Tag机制
在 RabbitMQ 的消费者代码中,Channel 和 tag 参数的存在是为了实现消息确认机制(Acknowledgment)和精细化的消息控制。 Channel 参数 作用 Channel 是 AMQP 协议的核心操作接口,通过它可以直接与 RabbitMQ 交互: 手…...
